辗扩参数对大型厚壁筒形件变形规律的影响
温慧华,王金亮,何文武,田继红,陈慧琴
(1.太原科技大学 材料科学与工程学院,太原 030024;2.山西省大型铸锻件工程技术研究中心,太原 030024)
护环是紧箍在发电机转子上的环筒形锻件,其传统的制造工艺流程包括冶炼-凝固-开坯-镦粗-冲孔-芯棒拔长-扩孔-平整等工序,属于多火次、多工序的热加工工艺,工艺过程冗长,材料利用率低,能耗高,锻造变形不均匀,热裂倾向严重[1]。上世纪90年代,太原科技大学提出了护环短流程制造技术[2],即电渣重熔(ESR)钢锭-模内冲扩-扩挤复合成形[3]或ESR空心钢锭-模内扩挤复合成形短流程工艺[4],并对该工艺的热变形过程和微观晶粒组织演变进行了系统的分析研究和试制,取得了阶段性的成果和应用。随着空心钢锭制造技术[5-6]的提高和大型辗环机的发展[7],本文提出了空心钢锭-轧制(辗扩)成形的护环制造短流程新工艺。该新工艺流程采用空心钢锭的主要质量特点在于,钢锭壁厚内外表面同时进行冷却,较快的冷速可以抑制较大的偏析率,提高材料的均质性,并在内表面形成较细的晶粒,提高了空心钢锭内表面质量[8]。电渣空心钢锭可以避免实心钢锭中心各种冶金缺陷的产生,且钢质纯净、基本无偏析、结晶组织均匀致密、化学成分均匀,为生产优质大型厚壁筒形件提供了高质量的空心钢锭。随后采用准稳态局部连续塑性变形的热辗扩轧制工艺控制成形,变形均匀,避免了操作复杂的芯轴拔长和芯轴扩孔的多火次锻造工序,以及其变形不均匀,开裂严重等问题,而且环筒件的轧制成形过程自动化和可控化程度高,生产效率高,是一种高效、节能、节材的先进的大型筒形件制造工艺。
国内外学者对环形件轧制(辗扩)有关的设备结构、运动关系、环坯设计、成形规律和工艺参数进行了系统深入的研究,理论较成熟。如Youngsoo Yea等[9]采用数值模拟研究了环件辗扩过程中的速度、压力分布以及滚压力等参数。Forouzana等[10]利用热力耦合方法对辗扩过程进行了建模与分析。国内武汉理工大学的华林教授等[11-12]对环件轧制进行了系统的研究,建立了环件轧制静力学、运动学以及动力学、几何学模型,揭示了环件轧制成形原理和规律;西北工业大学的杨合等学者[13]对环件热辗扩过程传热、变形和微观组织演变耦合进行了模拟分析。太原科技大学李永堂等[14-15]对大型环件和环件的铸辗成形工艺进行了理论分析、数值模拟和实验,研究了工艺参数、设备参数以及摩擦系数等对辗扩工艺和成形质量的影响。鉴于大型厚壁筒形件具有壁厚和筒身高的特点,其轧制变形的锻透性和稳定性等问题有别于一般环件的轧制成形。因此,需要详细分析变形区的应力-应变状态和金属流动规律,合理设计轧制成形工艺,才能实现筒形件轧制成形形状尺寸和组织性能的精确控制。锻透性问题是环筒件轧制成形的关键技术之一,不仅影响轧件的形状尺寸和内部质量,而且影响轧制过程的顺利进行。文献[11]指出,环件锻透是指塑性变形区穿透环件壁厚,并根据滑移线理论,建立了环件锻透条件。文献[16]采用数值模拟方法分析了变截面环件轧制的锻透性。对于厚壁筒的轧制成形,由于驱动辊和芯棍与环件的相对尺寸差别较大,驱动辊和芯棍与环件的接触弧长在轧制过程中是动态变化的。因此,本文采用数值模拟分析方法,探讨了厚壁筒形件轧制变形的锻透性问题,以期为厚壁筒形件轧制成形工艺设计提供理论依据。
1 大型厚壁筒形件辗扩工艺模型的建立
1.1 辗扩工艺模型的建立
300 MW护环成品尺寸φ1 543.2 mm/771.6 mm×902 mm.根据文献[17],确定轧制比为2.5.据此设计径向辗扩的矩形截面毛坯尺寸为φ712 mm/308 mm×902 mm,壁厚202 mm.根据文献[11]计算得出,驱动辊半径为500 mm,芯棍半径为145 mm时,该筒形件接触弧长为23.1 mm,则锻透所需的最小压下量为1.39 mm.
分别模拟分析了该筒件辗扩初始局部加载条件下(1.3)和连续轧制过程中(1.4)的变形规律,以获得不同辗扩工艺参数对大型筒形件壁厚的影响。图1(a)为简化的轧制静态研究模型图,模拟局部加载条件下,驱动辊无转速,芯辊沿筒形件径向进给的情况,其建立采用了网格细化技术,筒形件接触变形区的网格与其他区域网格的边长比为1:100,其中1为驱动辊,4为护环毛坯,5为芯辊;图1(b)为建立的大型厚壁筒形件的辗扩工艺模型图,模拟连续轧制条件下,筒形件在驱动辊作用下发生旋转运动,同时,芯棍沿筒形件径向进给,筒件发生内外径增大和壁厚减薄的变形,辗扩过程中,锥辊则起限制端面变形和平整端面的作用,其中2、3为导向辊,6、7为锥辊。

图1 辗扩工艺有限元模型Fig.1 The FEM model of ring rolling process
1.2 环件轧制锻透条件
环件锻透是指塑性变形区穿透环件壁厚根据文献[12],环件轧制塑性区穿透环件壁厚的力学模型,如图2a所示(L为接触弧长,ha为环件轧制变形区的平均壁厚)。该模型是建立在环件锻透相当于有限高度块料拔长(图2b)的理论基础之上的。根据滑移线理论,文献[12]得出的环件锻透条件为:
(1)

图2 环件轧制锻透模型图Fig.2 Ring rolling forging penetration model
由公式(1)计算得出,在壁厚为202 mm时,接触弧长为23.1 mm.但是实际轧制过程内外接触弧长并不相等,且内接触弧长在50 mm以上,有时高达100 mm,所以不能简单套用此公式,需要静态轧制模拟来确定最合适的辊系尺寸。
1.3 大型厚壁筒形件局部加载模拟参数
大型厚壁筒形件局部加载模拟模型用于模拟不同驱动辊半径、芯辊半径和筒形件内径(壁厚)时,筒形件的变形规律。模拟参数如表1,表2和表3所示。

表1 驱动辊半径参数(筒形件尺寸φ712 mm/308 mm×902 mm,芯辊半径145 mm)

表2 芯辊半径参数(筒形件尺寸φ712 mm/308 mm×902 mm,驱动辊半径500 mm)Tab.2 The radius of idle rollers(the cylindrical part:φ712 mm/308 mm×902 mm,the radius of the driving roller:500 mm)
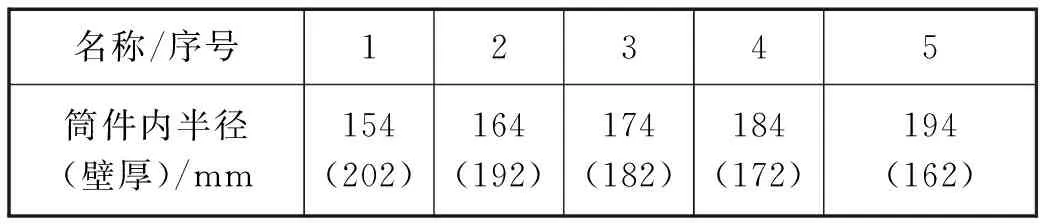
表3 筒形件内径(壁厚)参数(驱动辊半径500 mm,芯辊半径145 mm,筒件外径356 mm)
1.4 大型厚壁筒形件连续辗扩模拟参数
大型厚壁筒形件连续辗扩模拟模型用于模拟一定辊系和筒形件尺寸条件下,由不同最小压下量和筒形件转速决定的芯辊进给速度对轧制后筒形件内部应变分布的影响。筒形件尺寸φ712 mm/308 mm× 2 mm,轧制比2.5[17],驱动辊半径500 mm,芯辊半径130 mm,筒形件切向速度1.3 mm/s,芯辊进给速度分别取1.0 mm/s,1.3 mm/s,1.5 mm/s,1.8 mm/s和2.2 mm/s.
1.5 材料模型和模拟计算参数
大型厚壁筒形件材料为Mn18Cr18N护环钢,其应力-应变曲线由实验获得并输入DEFORM材料库中。模具材料选择DEFORM材料库中AISI—D3热作模具钢。环件初始温度1 050 ℃,轧 辊初始温度200 ℃,环境温度20 ℃,轧辊与筒件之间摩擦系数0.7,热传导系数11 N/(s·mm·℃),热交换系数0.02 N/(s·mm·℃),热辐射系数0.7 N/(s·mm·℃).
2 模拟结果与分析
2.1 辊系和筒件尺寸对加载区应变分布的影响
2.1.1 驱动辊尺寸对加载区应变分布的影响
图3为筒形件尺寸φ712 mm/308 mm×902 mm,芯辊半径145 mm时,不同驱动辊半径对加载区内外接触弧长的影响。可以看出,由于芯棍尺寸一定,所以图3中的内接触弧长基本不变,约为102.6 mm.当驱动辊半径从300 mm增加到700 mm时,外接触弧长分别为27.2 mm,30.2 mm,33.2 mm,30.2 mm和27.2 mm.外接触弧长的数值先增大后减小,在驱动辊尺寸为500 mm时,外接触弧长达到最大值33.2 mm.这是由于变量为驱动辊半径,驱动辊尺寸的和变化对内接触弧长的影响不大,这是由于内接触弧长并未与变量有直接接触,其变化较小,与外接触弧长直接接触,其影响较大,且在环件辗扩过程中,内外接触弧长越接近,加载区应变分布越对称,变形越均匀,越有利于环件辗扩的进行。所以,在芯辊和坯料尺寸一定时,驱动辊尺寸太小或太大都不利于环件的均匀变形,其半径取500 mm时,与芯辊的匹配性好。
图4为对应图3不同接触弧长条件下加载区内的应变分布(图中应变标尺范围均为0~0.01).由于驱动辊尺寸变化对内外接触弧长的影响不大(图3),所以,不同驱动辊半径条件下加载区内的应变分布也相似,即应变穿透筒形件壁厚的位置约在靠近内接触面的壁厚的1/4处。但是,图4(a)-(b)和(d)-(e)中的内接触弧长处均有应变为零的刚性区存在;而图4(c)中内接触弧长处有应变,且应变数值较大,应变分布的对称性好,有利于筒形件均匀扩大。从应变穿透筒形件壁厚所需的压下量来说,驱动辊尺寸从300 mm到700 mm,所需压下量分别为3.2 mm,3.1 mm,3.0 mm,3.2 mm和3.3 mm,即当驱动辊尺寸为500 mm时应变穿透壁厚所需的压下量最小,筒形件辗扩的锻透性容易满足,芯辊进给速度和轧制力也最小。这是因为当驱动辊尺寸为500 mm时,内接触弧长与外接触弧长最接近,对环件的作用力集中在接触区域,导致接触区域的应变值增大,环件内外层均发生变形,所以辗扩时应变穿透筒形件所需的压下量最小,此时轧制力也较小;若是接触弧长差距太大,轧制开始时,内层出现刚性区,环件内径不长大而外径长大,环件轧制非均匀变形程度增大,更有可能造成轧制不成功的情况。

图4 不同驱动辊半径下加载区内的应变分布Fig.4 Strain distributions in the loading region at different radius of driving rollers
综上分析图3和图4,从内外接触弧长情况、应变分布情况和压下量综合考虑,驱动辊半径为500 mm时,内外接触弧长最接近,有利于获得接近对称的应变分布,应变穿透筒形件壁厚所需压下量最小,实际轧制时芯辊进给速度和轧制力也最小。所以,筒形件和芯辊尺寸取上述尺寸,驱动辊半径取500 mm最佳。
2.1.2 芯辊尺寸对内外接触弧长和加载区应变分布的影响
图5为筒形件尺寸φ712 mm/308 mm×902 mm,驱动辊半径500 mm时,不同芯辊半径对加载区内外接触弧长的影响。芯辊半径为145 mm和140 mm时,内外接触弧长均约为100 mm和33 mm,内外接触弧长比约为3;芯辊尺寸在130 mm~110 mm之间时,内接触弧长分别稳定在57.3 mm、54.4 mm和48.7 mm,外接触弧长均稳定在21.1 mm,内外接触弧长之比约为2.5左右;当芯辊半径减小至100 mm时,内外接触弧长继续减小,内接触弧长约为42.2 mm,外接触弧长约为15.1 mm,内外接触弧长之比接近3.以上分析说明:当芯辊尺寸从图5(a)变化至图5(c)时,内接触弧长减小显著,内外接触弧长的长度最接近;当芯辊尺寸为图5(d)-(f)情况时,内接触弧长也在减小但减小速度很慢,且内外接触弧长差异增加。造成这一现象的原因是:由于毛坯内径在开始时与芯辊尺寸非常接近,芯辊尺寸的减小对内接触弧长影响较大;当芯辊尺寸与毛坯内径相差较大时,芯辊尺寸的减小对内接触弧长影响逐渐减小,其值稳定在一定范围内。综上,驱动辊半径500 mm,芯辊半径从145 mm变化到100 mm时,内外接触弧长之比在2.5~3之间。
图6为对应图5不同接触弧长条件下变形区内的应变分布。可以看出,随着芯棍半径的减小,变形区应变分布逐渐趋于对称分布,径向锻透所需的压下量也逐渐减小。当芯棍半径从图6(a)的145 mm减小到图6(c)的130 mm时,变形区应变分布已基本呈现对称分布,但是内接触弧长处的应变数值与外表面应变数值相比有较大差距,对应的锻透压下量为2.9 mm.芯棍半径减小到120 mm~100 mm之间,变形区应变分布和数值均接近对称分布,锻透压下量均为2.8 mm.这是由于:当芯辊尺寸较大时,即图6(a)-(b),内外接触弧长差异较大,对应的内外表面接触面积差异非常大,而相同的轧制力作用在内表面的应力远小于外表面应力,所以造成内外表面应变不同的情况;当芯辊尺寸逐渐减小,即图6(c)-(f),芯辊尺寸减小,内接触弧长随之减小,内外表面接触面积差异减小,轧制力作用在内表面的应力越来越大,与外表面的应力越来越相近。
综合考虑应变分布和压下量,以及后续的轧制变形,在上述筒形件和驱动辊尺寸条件下,芯棍半径取130 mm较为合适。
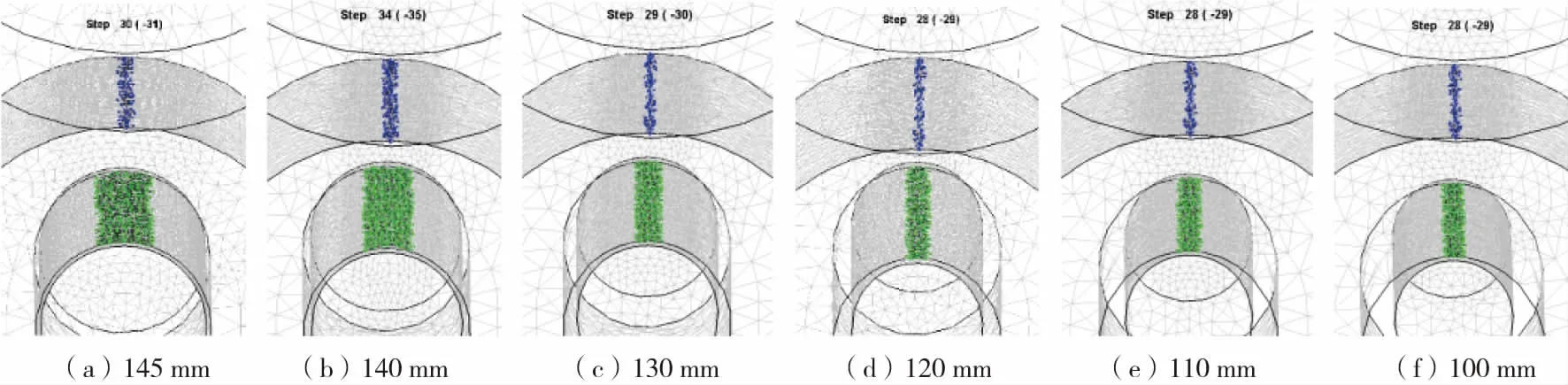
图5 不同芯辊半径下加载区的接触弧长Fig.5 Contact arc lengths in the loading region at different radius of idle rollers
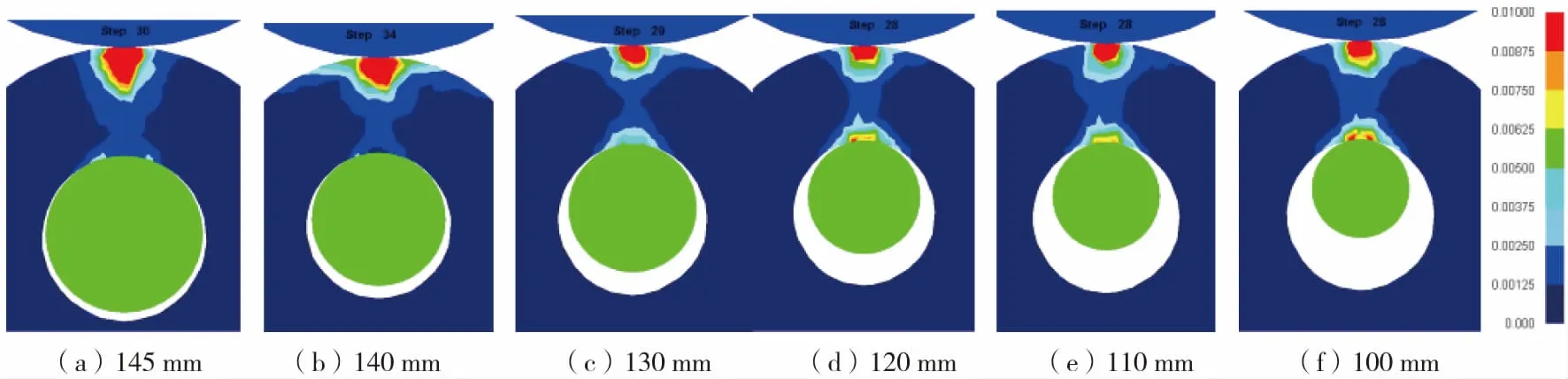
图6 不同芯棍半径下加载区内的应变分布Fig.6 Strain distributions in the strain penetration region under different radius of idle rollers
2.1.3 筒形件尺寸对内外接触弧长和变形区应变分布的影响
如图7、8所示,在辊系尺寸(驱动辊半径500 mm和芯辊半径145 mm)一定的条件下,通过增大筒形件内径,从而减小筒形件壁厚,分析接触弧长和应变分布情况。

图7 不同筒形件壁厚下加载区的接触弧长Fig.7 Contact arc lengths in the loading region under different thickness of cylindrical parts

图8 不同筒形件壁厚下加载内的应变分布Fig.8 Strain distributions in the loading region under different thickness of cylindrical parts
由图7可以看出,随着环件内半径的增大,即壁厚的减薄,内外接触弧长均逐渐减小。壁厚为202 mm时,内外接触弧长分别为102.6 mm和33.6 mm,内外接触弧长之比为3.1;壁厚在192 mm~172 mm之间,内接触弧长在60 mm~56 mm之间,与壁厚为202 mm相比减小显著,外接触弧长稳定在27.2 mm,内外接触弧长比在2.0左右,说明这一范围壁厚的减小对内外接触弧长之比影响较大;壁厚减薄到162 mm,内外接触弧长分别减小至53.7 mm和30.1 mm,内外接触弧长之比减小至1.8,此时壁厚的减小对内外接触弧长影响不大。造成这一现象的原因有两点:一是环件外半径与驱动辊半径不变,在静态模拟时外接触弧长变化很小;二是环件内半径逐渐增大而芯辊尺寸不变,当环件内半径从图7(a)变化至图7(b)时,环件内半径与芯辊半径数值接近,所以变化非常大;当环件内半径继续增大,其与芯辊半径的数值相差较大,内接触弧长减小幅度降低,所以变化较小。
图8为对应图7加载区内的应变分布情况。从图中可以看出,当壁厚为202 mm时,变形区内应变分布明显不对称,且内接触区域的应变值较小,筒件不容易发生变形,造成这一现象原因主要是环件内半径与芯辊半径非常接近,内接触弧长远大于外接触弧长,外表面接触面积小于内表面接触面积,而相同轧制力作用在外表面时应力大于内表面应力,所以外表面应变大于内表面应变;当壁厚减小至192 mm时,变形区的应变分布对称性最好,内接触区域的应变值较大,筒件易发生变形,这是由于环件内半径增大,内接触弧长显著减小,内外表面接触面积相近,造成内外表面应变相近的现象;当壁厚继续减小时,应变分布对称性没有发生改变,且内接触区域有刚性区出现,筒件内径不发生变形,这是因为环件内半径的继续增大,使得轧制力主要作用在芯辊与环件接触面的边缘区域,而接触面内部区域存在刚性区,对轧制时环件内半径的增大过程不利。从压下量分析,壁厚为202 mm时的压下量最大,为3.0 mm;当壁厚逐渐减小,压下量分别为2.2 mm,2.4 mm和2.4 mm,数值差异较小。
综合图7和图8,壁厚为192 mm时,内外接触弧长比在2.0左右,内接触弧长应变值较大,应变分布较均匀,加载区内应变分布对称性较好,所需的压下量为2.2 mm,较为合理。
2.2 芯辊进给速度对轧制后筒形件内部应变分布的影响
图9为在一定辊系(驱动辊半径500 mm,芯辊半径130 mm)和筒形件尺寸为φ712 mm/308 mm× 2 mm条件下,驱动辊转速2.6 rad/s,芯辊进给速度分别取1.0 mm/s,1.3 mm/s,1.5 mm/s,1.8 mm/s和2.2 mm/s时,辗扩结束后筒形件内部应变的分布。图9为筒件子午面内的应变分布。可以看出,筒形件子午面内的应变分布不均匀,大应变区分布在筒形件上下两端的局部区域内,分别达到29.52,15.72,10.16,10.23和9.02.当芯辊进给速度为1 mm/s时(图9a),环件成形尺寸不符合要求,上下两端变形极不均匀,且两端处的鱼尾和展宽缺陷严重,这是由于筒形件连续辗扩过程中的锻透性较差,最终使得环件成形尺寸达不到要求而辗扩失败。随着芯辊进给速度的增加,展宽逐渐减小,锻透性逐渐得到改善,这是由于增大芯辊进给速度相当于增大轧制力,在相同接触状态下,应力和应变随之增大,所以轧制过程中的锻透性得到改善,环件内半径和外半径均匀长大,上下两端边缘处的鱼尾和展宽也得到改善。当芯辊进给速达到1.5 mm/s时(图9c),继续增加芯辊速度,展宽造成的应变不均匀性的改善程度基本趋于平稳。说明随着芯辊进给速度的增加,筒形件端部应变值越来越小,后期逐渐稳定。除端部外,筒形件子午面高度其余大部分区域的应变较均匀,分别达到3.69,1.97,1.27,1.27和1.12.当芯辊进给速度达到2.2 mm/s时(图9e),筒形件中部大部分区域沿壁厚的变形不均匀性又逐渐显著,这是因为芯辊进给速度的增加改善了锻透性,使得环件内外表面区域的大应变区域增加,环件中部的小应变区域减小,造成环件内外表面变形较大,内部变形较小,造成其沿壁厚放心的不均匀长大。筒形件中部大部分区域的应变平均值分别为3.69,1.97,1.69,1.69和1.69.而芯辊速度为1.5 mm/s以上时,筒形件中部的应变分布较均匀,即环件内径与外径的变形程度相近,环件在轧制过程中内径与外径可以均匀长大。由图9a-e分析可得,芯辊进给速度取1.5 mm/s~1.8 mm/s时,对环件整体应变分布均匀性影响较小,即环件成形效果相近。
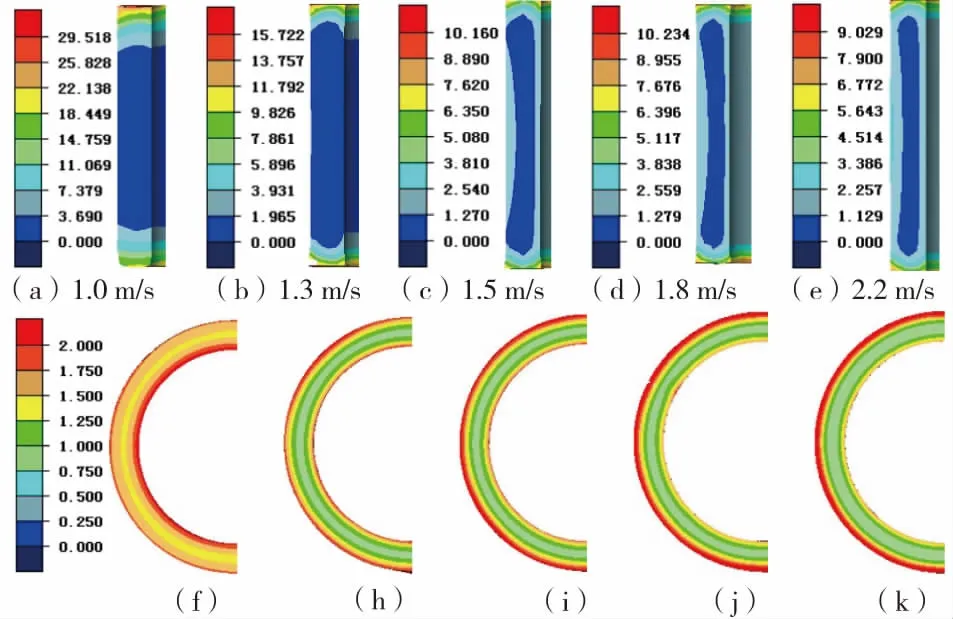
图9 不同芯辊进给速度下辗扩后筒形件内的应变分布Fig.9 Strain distributions in the cylindrical parts at different feeding velocities of the idle roller
为了进一步分析筒形件中部区域变形的均匀性,图9(f)-(k)给出了不同芯辊速度条件下辗扩结束后,沿筒形件中部壁厚的径向应变分布(应变分布标尺统一为0~2.00).当芯辊进给速度为1 mm/s时(即图9(f)),径向应变较高,且内径应变较高,内外变形程度极不均匀,最终环件轧制失败。当芯辊进给速度为1.3 mm/s~1.8 mm/s时(图9(h)-(j)),径向应变分布的规律一致,应变区域分布相近,但环件外径处的大应变区域越来越大,中径处的小应变区域分布大致相同,在壁厚区域的占比分别均约为30%,此现象原因是:芯辊进给速度的增加使轧制力增大,环件外表面区域的接触面积不变,应变也随之增大,内外表面的应变差异减小,但芯辊速度的继续增加,环件外接触表面的应变超过内接触表面的应变,使得环件外表面的变形程度大于内表面的变形程度,所以造成外表面区域的应变越来越大的现象;当芯辊进给速度增加到2.2 mm/s时(图9(k)),外径处的大应变区域继续增大,中径处的小应变区域增大,在壁厚区域的占比增加至40%,且不利于环件径向方向的均匀变形。所以,由图8(f)-(k)分析得出,芯辊进给速度取1.3 mm/s~1.8 mm/s较为合适。
综合图9(a)-(k)的轴向和径向应变分布均匀性规律,同时考虑实际辗环过程的顺利进行和设备的轧制力,在此坯料和辊系参数的条件下,芯辊进给速度取1.5 mm/s最佳。
图9中芯辊进给速度1.0 mm/s,1.3 mm/s,1.5 mm/s,1.8 mm/s和2.2 mm/s对应的设计进给量分别为1.72 mm,2.24 mm,2.58 mm,3.10 mm和3.78 mm.也就是说,对于图9计算的模拟参数下的实际辗扩工艺,最佳的芯辊进给速度1.5 mm/s对应的最小进给量为2.58 mm是更为合理的。
3 结论
(1)分析获得了驱动辊和芯辊尺寸对φ712 mm/308 mm×2 mm筒形件轧制接触弧长和变形区应变分布的影响规律,结果表明,驱动辊半径为500 mm,芯辊半径为130 mm,筒形件轧制的内外接触弧长之比最小,变形区应变分布的对称性最好,相应锻透所需的最小压下量为3 mm.
(2)当辊系尺寸确定,通过改变φ712 mm/308 mm×2 mm筒形件内径(壁厚),获得了筒形件内径(壁厚)对轧制接触弧长和变形区应变分布的影响规律。结果表明,筒形件内径164 mm(壁厚192 mm)时,筒形件轧制的内外接触弧长之比最小,变形区应变分布的对称性好,锻透所需的压下量最小为2.2 mm.
(3)当筒形件尺寸为φ712 mm/308 mm× 2 mm,辊系尺寸采取结论1中结果,驱动辊转速为2.6 rad/s时,模拟结果表明:芯辊进给速度为1.5 mm/s时,整个辗扩过程中均满足锻透性条件,筒件发生壁厚方向的整体变形,且辗扩结束后,筒形件内部的应变分布均匀性好,筒形件中部大部分区域的应变平均值达到1.69,其对应的最小每转进给量为2.58 mm.

