求解信赖域子问题的Adams四阶预报校正格式算法

范晓宇，李丹琳，王希云

(1.太原科技大学应用科学学院，太原 030024；2.合肥工业大学数学学院，合肥 230601)

求解二次模型信赖域子问题[1-2]是信赖域算法中极其重要的步骤，也就是求解如下形式：

(1)

当Δ变化时，(1)的解δ在空间构成一条曲线，称为最优曲线[3]。

传统的精确求解方法可以求解二次模型子问题，但过程较为繁复。利用该方法，可得到最优曲线的参数方程。在参数方程的基础上，可建立最优曲线的微分方程模型。模型如下所示[4]：

(2)

此时求解信赖域子问题就变成了求解微分方程问题。据此思想，文献[4]-[9]在求解微分方程模型时，联合一些常见、简单的单步法公式构造折线，进而替代最优曲线。分别提出了求解二次模型子问题的显式欧拉算法、隐式欧拉算法、平均欧拉算法以及R-K类算法。为了充分利用已有的信息，文献[10]联合多步法公式构造折线，进而替代最优曲线。提出了求解二次模型子问题的Adams多步法算法。求解子问题时，文献[10]中的Adams四阶显式算法计算简单，Adams四阶隐式算法精度高，为发挥各自优点，进一步提高精度，本文联合求解微分方程时常用的Adams四阶预报—校正格式[11]：

(3)

fk=-(B+μkI)-1δk，(k=n，n-1，n-2，n-3)

提出了Adams四阶预报—校正格式算法，求解信赖域子问题。文章分析了算法对应折线的性质，在理论上给予证明，在实验上给予验证。通过与文献[10]提出的Adams四阶显式算法、Adams四阶隐式算法的数值实验比较，验证了该算法的数值解可达到更高的精度，是可行的且是一种数值效果较好的新算法。

1 Adams四阶预报—校正格式折线的构造

第一步：从初始点P0(μ0，δ0)开始，其中μ0=0，δ0=-B-1g，选取步长h，用公式：

(4)

第二步：由常用的经典Runge-Kutta公式：

计算δ1.记:

则记为:

(5)

从而得到下一个节点P1(μ1，δ1)，其中μ1=μ0+h.同理可得到节点P2(μ2，δ2)，P3(μ3，δ3).

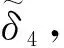
δ(τ)=

(6)

则步长h需满足下式：

h=

(7)

2 Adams四阶预报—校正格式折线的性质

引理1设B对称正定，则当0≤n≤2时，不等式①成立。

则当3≤n≤N-1时，不等式②成立。

由引理1，可知步长h为正。

定理1设B对称正定，且0≤n≤2时有(8)式成立；

gT(fn1+2fn2+2fn3+fn4)+

(8)

n≥3时有(9)式成立。

(9)

则δ(τ)满足：

(1)‖δ(τ)‖2关于τ为单调减函数。

(2)q[δ(τ)]关于τ为单调增函数。

证明：(1)当τ∈[μ0，μ1]，即τ∈[0，h0]时，

则：

由(7)式与引理1可知，

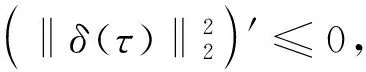
同理τ∈(μ1，μ2]，τ∈(μ2，μ3]时，

因而，‖δ(τ)‖2在区间[μ0，μ1]，(μ1，μ2]，(μ2，μ3]上递减。

当∀τ∈(μi，μi+1]即(τ-μi)∈(0，hi]，3≤i≤N-1

则:

由(7)式与引理1可知，

(2)当τ∈[μ0，μ1]，即τ∈[0，h0]时，

B(f01+2f02+2f03+f04)

2f03+f04)+δ0TB(f01+2f02+2f03+f04))

由已知条件(8)，可得(q[δ(τ)])′≥0，τ∈[μ0，μ1].同理(q[δ(τ)])′≥0，τ∈(μ1，μ2]，(μ2，μ3].因而，q[δ(τ)]在区间[μ0，μ1]，(μ1，μ2]，(μ2，μ3]为递增，得证。

当∀τ∈(μi，μi+1]即(τ-μi)∈(0，hi]，3≤i≤N-1时，

q[δ(τ)]=

由已知条件(9)得(q[δ(τ)])′≥0，τ∈(μi，μi+1].

因而，q[δ(τ)]在区间(μi，μi+1]，i=3，…，N-1为递增，得证。证毕。

3 Adams四阶预报—校正格式算法

步0.给定g，B，Δ.令n=0.

步1.令δ0=-B-1g.

步2.若Δ≥‖δ0‖2，则取δ*=δ0，此时计算终止。否则，令n=n+1，转步3.

(R-K法计算起步值)对n=1，2，3，做步3到步4.

步3.计算δn。由公式(4)和经典RK公式计算

步4.若Δ≥‖δn‖2，则:

其中：

计算终止。否则令n=n+1转步3.(Adams四阶预报-校正法计算δn) 对n=4，5…做步5到步6.

步6.若Δ≥‖δn‖2，

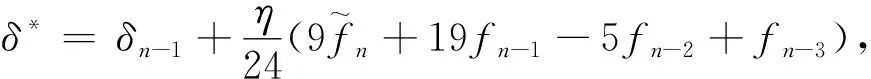
计算终止。否则令n=n+1转步5.

4 Adams四阶预报—校正格式算法的适定性

定理2在定理1成立的情况下，B对称正定，利用Adams四阶预报—校正格式折线δ(τ)求解信赖域子问题的极小点，解在信赖域边界上，且η满足：

其中:

证明：分情况进行讨论：

①当n=1，2，3时，η满足方程：

其中：

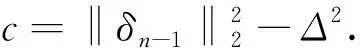
②当n=4，5，…时，η满足方程：

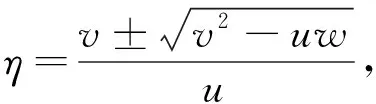
其中：

5 数值实验

对于子问题(1)的求解，步长固定为h=0.1，信赖域半径Δ依次改变，依据本文提出的新算法，对附录中选取的两个简单的测试函数，分别进行数值实验(参考文献[12]).算法获得最优解的时间复杂度O(n2).表1和表2为该算法的数值结果，以及与文献[10]提出的Adams四阶显式算法、Adams四阶隐式算法数值结果的比较。

表1 测试函数1的数值结果

表2 测试函数2的数值结果

比照表1和表2的数值结果，有如下结论：当信赖域半径Δ≥‖B-1g‖2时，三种算法求得的数值结果是完全相同的(此时为牛顿算法)。在信赖域半径Δ<‖B-1g‖2时，对Funtion1进行实验，Adams四阶预报-校正格式算法的效果一直比Adams四阶显式算法的效果要好。当信赖域半径Δ=9和9.2时，Adams四阶隐式算法的效果略微好于Adams四阶预报-校正格式算法的效果；而信赖域半径取其他值时，通过对比数值结果，发现Adams四阶预报-校正格式算法比Adams四阶隐式算法更好。对于Funtion2，Adams四阶预报-校正格式算法的数值结果均好于Adams四阶显式算法、Adams四阶隐式算法。因而本文提出的Adams四阶预报-校正格式算法是一种有效且可行，数值效果较好的新算法。

其中，对于测试函数Funtion1

‖B-1g‖2=9.42，

对于测试函数Funtion2‖B-1g‖2=10.46

附录：测试函数

Function1: Powell’s 4-variable function在初始点(2,5,3,6)T处的信赖域子问题。

s.t.‖δ‖2≤Δ

Function2: Wood-Colville’s function在初始点

(3,8,2,4)T处的信赖域子问题.

s.t.‖δ‖2≤Δ