基于PCA降维的成对约束半监督聚类集成
黄欣辰,皋 军,黄豪杰
(1.盐城工学院信息工程学院,江苏 盐城 224002; 2.江苏科技大学计算机学院,江苏 镇江 212003)
0 引 言
聚类分析的目的是根据对象之间的相似度对对象分组,使得簇内对象相似度尽量高,而簇间对象相似度尽量低,簇内相似性越大,簇间差别越大,聚类性能越好[1]。但单个的聚类方法不能令人产生满意的结果,聚类集成是一种将多个不同的聚类结果进行合并,能够获得比传统聚类算法更好聚类结果的方法[2]。目前聚类集成的研究主要集中在无监督学习领域中,没有考虑到用户或者专家提供的先验知识。而半监督聚类集成将少量带有标签的数据代入到聚类集成中,监督与指导集成过程,最终获得更加优越的聚类结果,使得整个过程更具稳定性、准确性和鲁棒性[3-5]。
常见的半监督聚类方法有3种。第1种是基于约束的半监督聚类[4],样本两两之间包含了一组成对约束信息,即正约束(must-link)和负约束(cannot-link)信息,通过它们能很有效地指导聚类过程。must-link约束规定:若2个样本满足must-link约束,则2个样本在聚类时一定被划分到同一个簇中。cannot-link约束规定:若2个样本满足cannot-link约束,则2个样本在聚类时一定被划分到不同簇之中。第2种是基于距离的半监督聚类[6],这类算法是根据样本之间的约束信息来构造一个距离度量函数,对样本点进行划分,形成分组。第3种是基于约束和距离的半监督聚类算法[7],它是第1种和第2种方法的融合。
随着大数据时代的到来,各种各样的数据出现在人们生活中,如文本数据、图片数据、声音数据、视频数据、基因数据等,且这些冗长的数据越来越呈现出高维性的特点,使得很多算法在数据分析过程中引起“维数灾难”[8-9]。在实际生活中,通常先对高维数据进行降维处理,然后再进行后续操作。
针对上述问题,本文在现有的半监督降维聚类算法基础上,提出一种基于PCA降维技术的成对约束半监督聚类集成算法(Semi supervised clustering ensemble with pairwise constraints based on PCA dimension reduction, SSCEDR)。首先通过PCA主成分分析对原始数据进行降维,然后结合半监督聚类集成技术,在降维后的空间中将成对约束等先验知识代入到聚类集成过程,得到最终的聚类结果。在多组数据集上进行的实验表明,SSCEDR算法能够提升聚类质量,取得更好的聚类结果。
1 PCA降维
降维是一种对高维数据进行维数约简的方法,一般根据高维数据特征的重要性,有选择地保留一些重要特征,实现数据从高维到低维的转化。常见的降维算法有奇异值分解(SVD)[10]、主成分分析(PCA)[11]、线性判别分析(LDA)[12]、因子分析(FA)[13]、独立成分分析(ICA)[14]。
本文选用的降维算法是PCA(Principal Componet Analysis),即主成分分析法,是一种应用十分普遍的线性降维算法。主成分分析的核心思想是将n维特征映射到k维特征,得到一种新的正交特征,即主成分,它是在原有n维特征的基础上重建的k维特征[15]。
给定一组数据:X=[x1,x2,…,xn],降维的目标是要找出一个投影矩阵W=[w1,w2,…,wd],使得数据的低维表示Y=WTX能够保留原有高维数据的原始结构。PCA需要找到数据方差最大的方向,定义目标函数为:

=arg max Tr(WTSW)
(1)
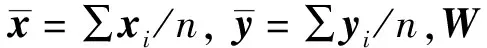
它的衡量指标是数据方差,数据间的方差越大,包含数据的原始特征信息越多,数据间的方差越小,包含数据的原始特征信息就越少。PCA就是在尽可能地保留原始数据重要特征的基础上,对数据进行降维,将高维数据投影到数据方差最大的方向组成新的子空间[16]。
(2)
G(k)为方差累计贡献率,也叫特征值累计贡献率,当累计贡献率大于90%时,一般认为能足够反映原来的数据信息,此时对应的k就是降维后的维数。
2 基于成对约束的半监督聚类集成
常见的半监督聚类算法有基于约束的方法(CBSSC)[17]、基于距离测度函数学习的方法(DBSSC)[18]、结合约束与距离的半监督算法(CDBSSC)[19]。受文献[20]的启发,本文选择基于约束的方法,来指导半监督信息的添加,引入一种基于成对约束的半监督聚类集成算法(Semi supervised clustering Ensemble based on pairwise constraints,SSCE)。
基于成对约束的半监督聚类集成可分为2个步骤:1)输入数据集,运行常用聚类分析算法,输出聚类成员集P={p1,p2,…,pH},这一步称为聚类成员生成;2)添加半监督信息,得到半监督相似矩阵S′,输出最终结果Pf,这一步为半监督共识函数设计[21]。下面着重对第二步予以阐述。
定义1must-link集合M={(xi,xj)},若(xi,xj)∈M,则表明数据xi和xj必属于同类,即xi和xj满足正关联约束关系。
定义2cannot-link集合C={(xi,xj)},若(xi,xj)∈C,则表明数据xi和xj必属于不同类,即xi和xj满足负关联约束关系。
故可用aij来表示样本点i和样本点j之间的相似度,aij用公式(3)表示:
(3)
即样本点i和j满足must-link约束aij=1,否则aij=0。
根据公式(3),能够得到包含must-link约束信息的矩阵M和包含cannot-link约束信息的矩阵C。矩阵M和矩阵C的维度与数据集X的相似性矩阵S相同。其中S=(s(xi,xj))N×N,s(xi,xj)=NMI(P(i,:),P(j,:))。
加入半监督信息后的相似性矩阵用D表示,计算公式如公式(4):
D=S-C+M
(4)
因为矩阵S、M和C的取值范围都在0~1,所以矩阵D的取值范围在-1~2之间,因此需要对矩阵D继续优化。如果2个样本的相似度大于1,则一定是同一类,故令它们相似度为1;如果2个样本的相似度小于0,则一定是不同类,故令它们相似度为0。因此可用公式(5)来优化矩阵D,获得半监督相似性矩阵S′:
(5)
基于成对约束的半监督聚类集成算法。
输入:数据集X={x1,x2,…,xN},簇个数k,聚类成员个数H。
1)运行k-means算法H次,每次随机选取初始质心,生成H个初始聚类成员;形成集成成员集P;
2)根据公式(3)~公式(5)得到相似性矩阵S′;
3)计算拉普拉斯矩阵L的最小特征值和对应特征向量,构建特征向量空间F;
4)在特征向量空间F中运行k-means算法得到最终聚类结果Pf。
输出:最终聚类结果Pf。
3 基于PCA降维的半监督聚类集成算法
基于上面的描述,本文提出一种基于PCA降维技术和成对约束的半监督聚类集成算法,首先通过PCA降维对原始高维数据进行降维,将原始数据降维到k维,并最大限度地保持原有数据集的一些重要特征,然后对得到的降维后的数据集进行基于成对约束的半监督聚类集成,其步骤如下:
输入:数据集X={x1,x2,…,xN},簇个数k,聚类成员个数H.降维后的维数d。
1)数据降维:
②计算样本的协方差矩阵XXT,并进行特征值分解;
③取最大的d个特征值所对应的特征向量(ω1,…,ωd)组成特征向量矩阵W;
④将数据转化到d维空间中,即Y=WTX。
2)对数据集Y,运行k-means算法H次,每次随机选取初始质心,生成H个初始聚类成员,形成集成成员集P。
3)根据公式(3)~公式(5)得到相似性矩阵S′。
4)计算拉普拉斯矩阵L的最小特征值和对应特征向量,构建特征向量空间F。
5)在特征向量空间F中运行k-means算法得到最终聚类结果Pf。
输出:最终聚类结果Pf。
4 实 验
4.1 实验数据集和评价标准
为了验证算法的有效性,实验中共选用了8组数据集,其中4组UCI数据集,2组手写体图像数据集,2组人脸数据集。样本数从148到2500不等,类别数从2到40不等,原始维数从13到1024不等。详细数据见表1。
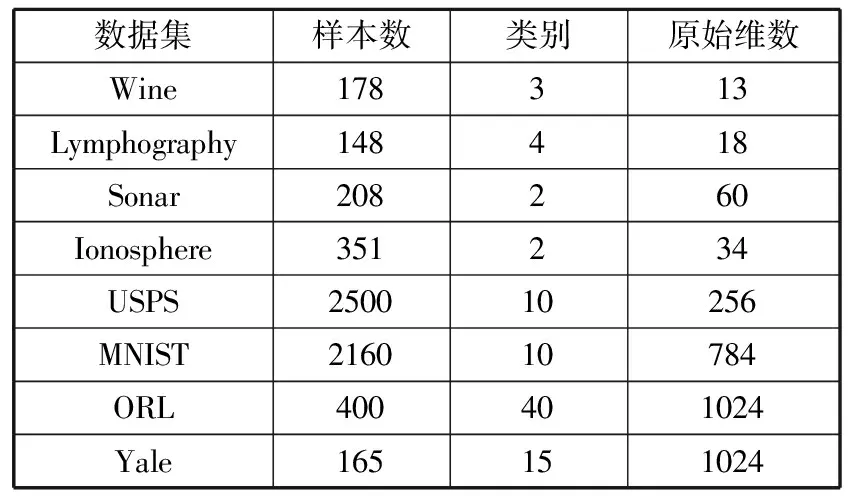
表1 实验数据集
因为所选的数据集类别标签已知,真实的类别标签可以为各类评价指标使用。实验采用Micro-p[22]这种常见的聚类性能评价指标来判断聚类效果。
Micro-p具体公式为:
其中,k为数据集的类别数,n是数据集中对象的总数,ai是聚类结果中正确分到第i个类的个数。显然Micro-p值越大,聚类结果和真实类别标签越匹配,当聚类结果和真实类别标签一一对应时,Micro-p值达到最大值1。
4.2 实验设计
本文提出一种基于PCA降维技术的成对约束半监督聚类集成算法(SSCEDR),实验的目的是验证所提的算法能否获得较好的聚类效果。实验分为2部分:1)对数据集进行PCA降维,选择合适降维维度,并在UCI数据集上测试算法的基本能力;2)在手写体数据集和人脸数据集上,将本文提出的算法SSCEDR与其他主流算法进行对比。对比算法分为2类,传统的聚类集成算法和常见的半监督降维算法。传统的算法包括半监督聚类集成算法SSCE、无监督聚类集成算法CSPA、HGPA。常见的半监督降维算法包括基于约束的半监督降维SSDR、半监督判别分析SDA以及约束Fisher判别分析cFDA。为了实验具有可对比性,实验对数据集以k-means算法,运行100次,生成初始聚类成员集P={p1,p2,…,p100},作为几种聚类集成算法的输入。
4.3 实验结果
4.3.1 PCA降维实验结果
图1显示了PCA降维算法在各个维度的特征值累计贡献率,通过图1可以看出随着降维算法维度的增加,特征值贡献率先是快速增长,达到一定的维度后就平稳增长。当特征值贡献率达到0.9时,意味着只有约10%的信息被丢失,此时降维效果最佳。通过实验发现当数据集Wine降到7维、Lymphography降到10维、Sonar降到16维、Ionosphere降到16维、USPS降到22维、MNIST降到90维、ORL降到60维、Yale降到50维时,特征值贡献率均超过了0.9,足够能反映原始变量的信息,故选择此时的维度,作为降维后的数据集维度。
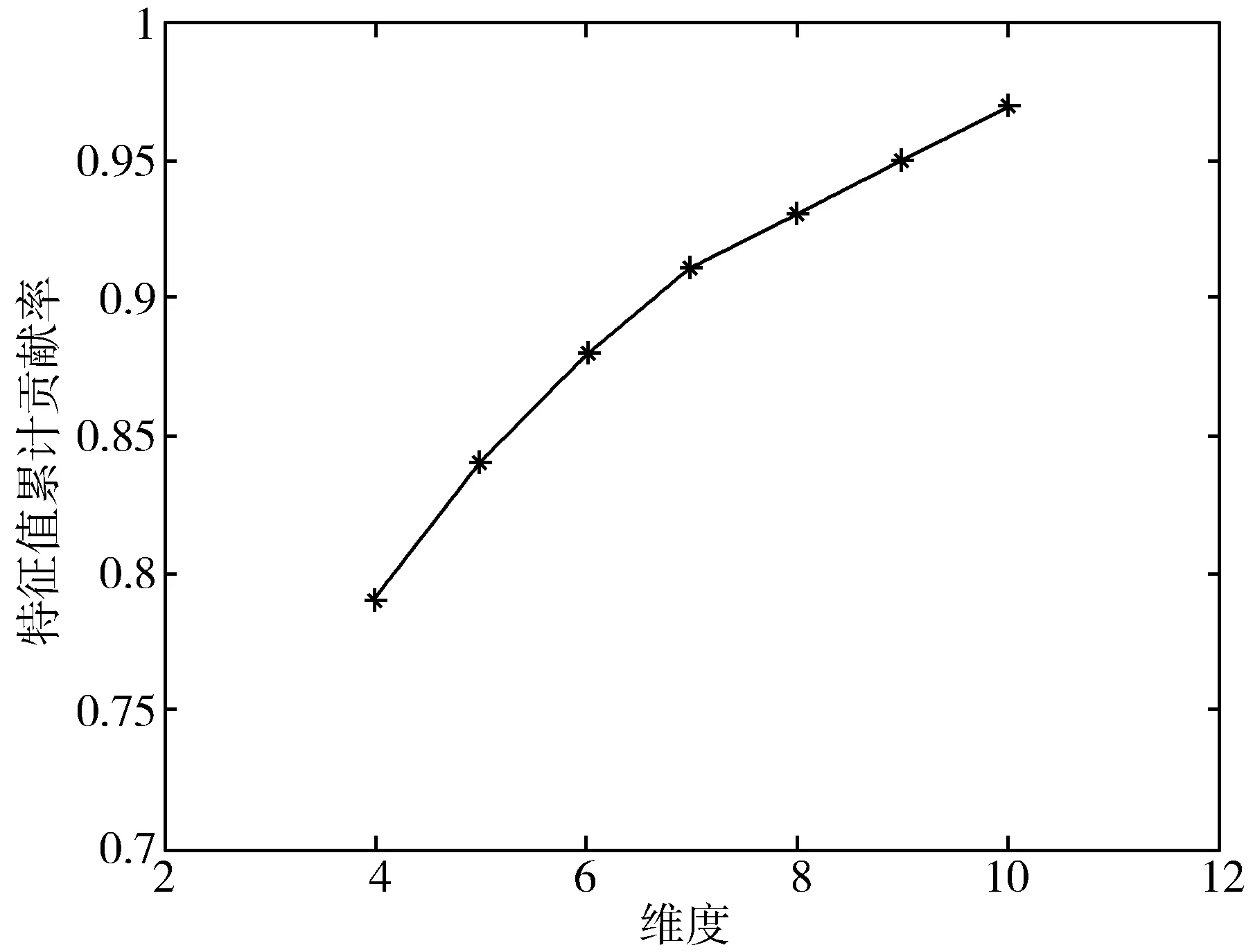
(a)Wine
更新后的实验数据集信息如表2所示。
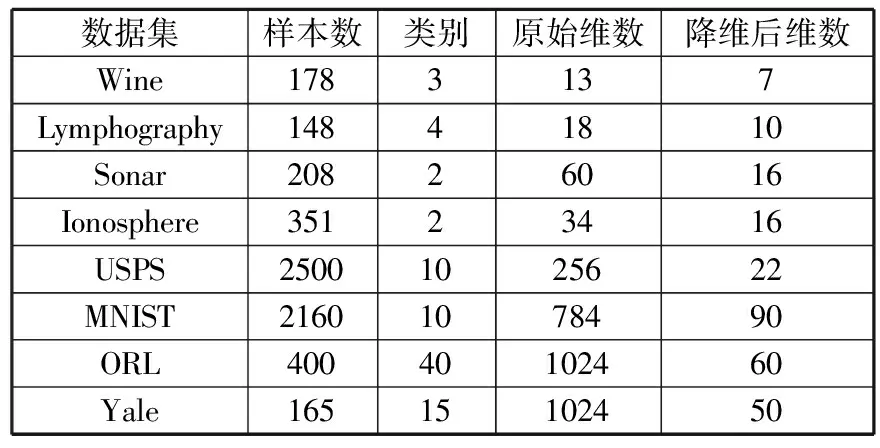
表2 降维后的实验数据集
4.3.2 测试算法基本聚类能力
UCI数据集常用来测试聚类算法的聚类效果。本文通过测试UCI数据集的4个数据子集:Wine数据集、Lymphography数据集、Sonar数据集、Ionosphere数据集来表明本文方法的基本聚类能力。表3与图2显示了本文算法SSCEDR在UCI数据集上的Micro-p值。
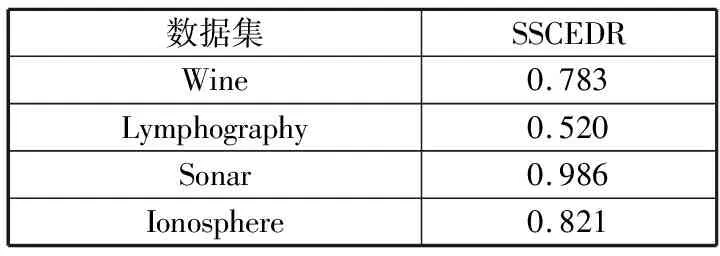
表3 SSCEDR在UCI数据集上的表现

图2 SSCEDR在UCI数据集上的Micro-p值
通过表3可以发现PCA+SSCE在UCI数据集Wine、Sonar、Ionosphere上的Micro-p值均超过了0.75,具有不错的聚类能力。为了更好验证SSCEDR算法的聚类效果,实验将本文算法与其他主流聚类集成算法在高维数据集上结果进行比较。
4.3.3 与其他聚类算法进行对比
在大容量数据集上进行实验,能更好地验证聚类算法性能。本文在大容量数据集USPS、MNIST、ORL和Yale上,将本文提出的算法SSCEDR与传统的算法SSCE、CSPA、HGPA等算法和半监督降维算法SSDR、SDA、cFDA进行比较。
表4展示在大容量数据集上,本文算法SSCEDR与传统聚类集成算法的Micro-p值,为了更直观地比较算法的Micro-p值,将表4中聚类集成算法的Micro-p值以柱状图的形式展示在图3中。
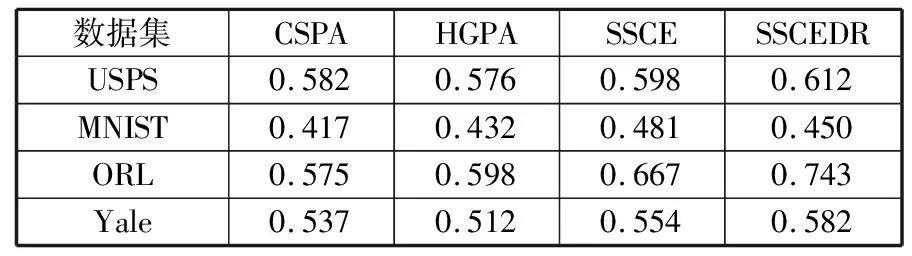
表4 与传统算法在数据集上的实验结果比较
观察表4和图3,可以更直观地发现:
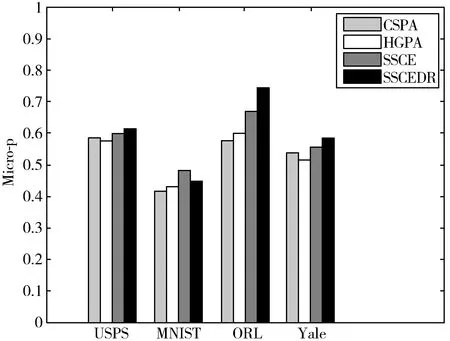
图3 本文算法与传统算法的结果比较
1)在实验所取的4个大容量数据集上,本文算法SSCEDR和半监督聚类集成算法SSCE取得的Micro-p值均高于无监督聚类集成CSPA和HGPA的Micro-p值。这表明加入成对约束信息的半监督聚类集成算法,能在聚类集成过程中,更好地指导数据聚类。与无监督聚类集成相比,半监督聚类集成能取得更好的聚类结果。
2)观察柱状图可以发现,除了在手写体数据集MNIST上,SSCEDR算法取得的Micro-p值低于SSCE算法的值,在其他3个数据集上都取得了最高的Micro-p值,且相对于其他算法有较明显的优势。这说明结合降维技术的半监督聚类集成,在实验数据集上取得了较好的聚类结果。
表5展示了本文算法SSCEDR与其他的常见的半监督降维算法在数据集上的结果,为了方便比较它们的Micro-p值,将表5中的实验结果以柱状图的形式展示在图4中。
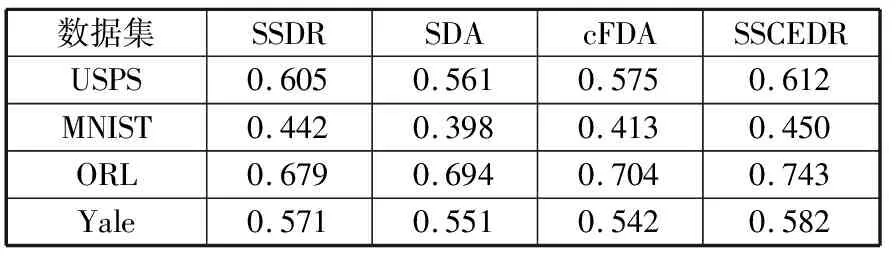
表5 与其他半监督降维算法在数据集上的结果比较

图4 本文算法与其他降维算法的结果比较
观察表5和图4可以发现,在数据集USPS、MNIST、ORL和Yale上,本文提出的基于PCA降维的成对约束半监督算法相比较其他半监督降维算法均取得较高的Micro-p值,这表明结合PCA降维的半监督聚类集成,在大容量数据集上取得了比较好的聚类结果。
总体来看,在聚类性能方面,半监督聚类集成算法较优于无监督聚类集成算法,本文提出的SSCEDR算法相比较于传统的无监督聚类集成算法、半监督聚类集成算法以及常见的半监督降维算法更具有优势,在多组数据集上都获得了较好的聚类结果,因此本文提出的结合降维技术的半监督选择聚类集成算法能提高半监督聚类集成算法的聚类效果。
5 结束语
本文在现有的半监督聚类集成算法基础上,提出了一种基于PCA降维的成对约束半监督聚类集成算法。该算法首先通过PCA降维技术,将高维数据转化为低维数据,然后在降维空间上进行半监督聚类集成,添加成对约束信息指导聚类过程,使得算法的聚类性能得到提高。实验结果表明,结合PCA降维的半监督聚类集成算法性能相较传统的无监督聚类集成算法和半监督聚类集成算法有了一定的提升,且比一些常见的半监督降维算法更具优势,在某些数据集上效果明显。但是算法的有效性和稳定性还需要进一步提高,如数据集降维后的维数是否能保证原始数据特征不丢失、数据间的成对约束是否正确、聚类成员个数的设定等,都可能影响算法的最终性能。

