基于MATLAB 的商用车平顺性优化与分析
何水龙,陈科任,叶明松,蒋占四
(1.桂林电子科技大学机电工程学院,广西 桂林 541004;2.东风柳州汽车有限公司,广西 柳州 544005)
1 引言
随着社会的进步和人们生活水平的提高,使用者对车辆平顺性也提出了更高的要求[1],而商用车平顺性包括了两层含义:(1)控制振动与冲击对乘员舒适性的影响在一定范围内;(2)保持商品完好性。目前研究大多仅对乘员座椅处的平顺性进行分析,缺少考虑车厢货物处振动水平情况。
目前大部分基于MATLAB 的汽车平顺性优化都存在优化变量与目标函数和约束条件之间为隐式函数关系式的缺点,不利于优化实现。为此,学者们进行了大量研究,提出许多处理方法,如:采用响应面模型近似的表达优化目标与约束条件之间的显式关系[2-4];通过罚函数将约束问题转化为无约束问题[5-6];利用考虑公差区间不确定性优化方法,将优化目标与约束条件进行确定性转化,得到区间不确定性优化模型[7],它们解决了非显式问题,但优化效率与可靠性仍有提升空间。
为有效提升商用车平顺性优化效率与可靠性,同时分析驾驶室振动与货箱振动对优化变量改变的响应情况,基于MATLAB提出一种商用车平顺性优化方法:以驾驶室与货箱加权加速度均方根值为改进目标函数,确保同时提升乘员舒适性和货物安全性,并通过调用仿真模型获得目标函数评价(目标适应度值);运用均匀设计法设计优化变量组合,获得约束条件对优化变量的显式关系式;最后基于MATLAB 实现仿真优化,与多软件联合优化方法相比避免了不同软件间数据传递误差,节约优化时间。
2 商用车模型建立
2.1 六自由度振动模型
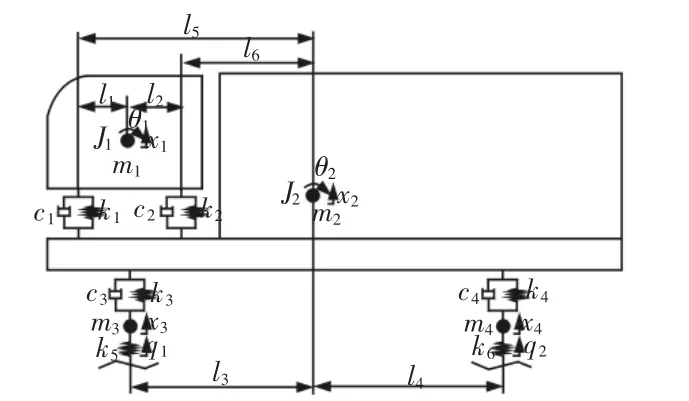
图1 六自由度振动模型Fig.1 Six-DOF Vibration Model

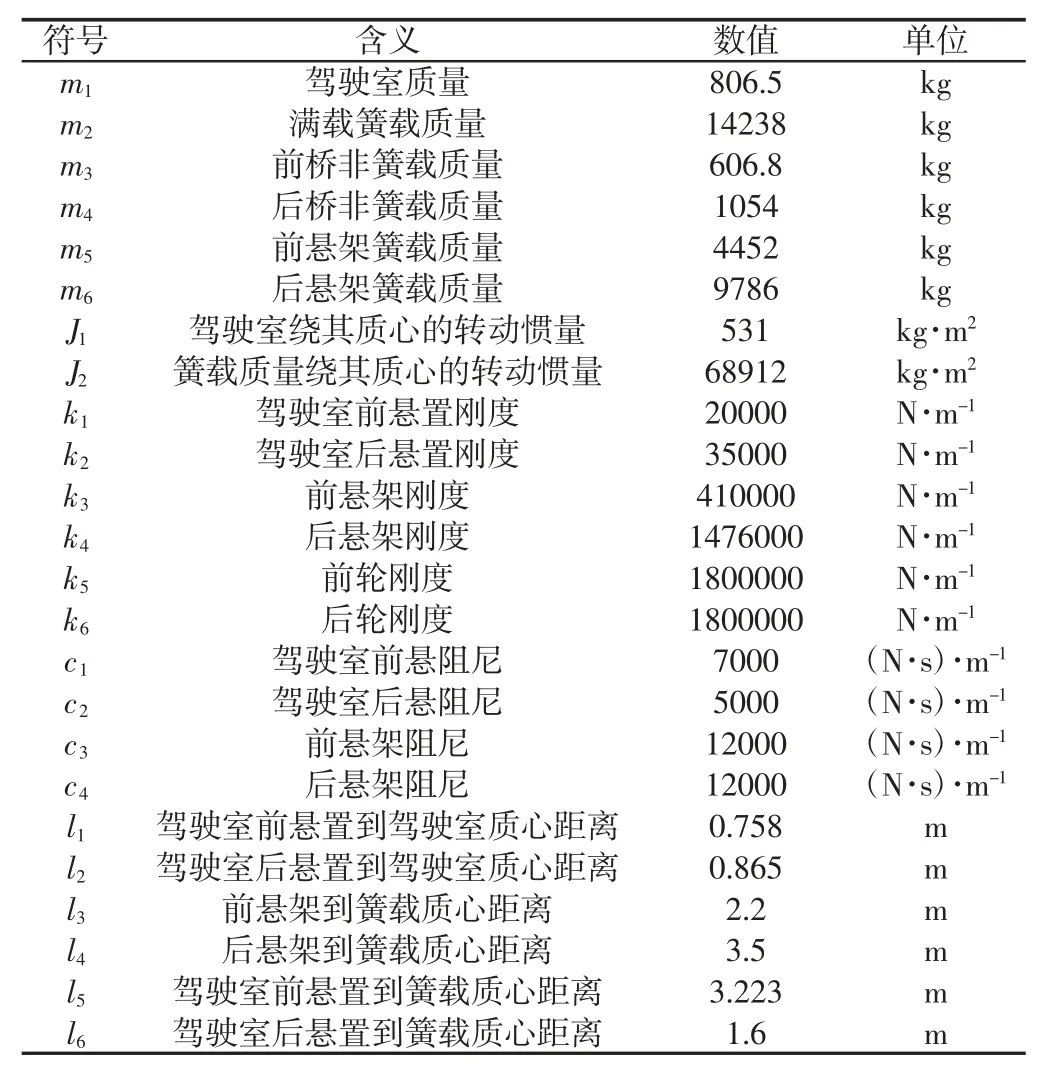
表1 六自由度振动模型参数Tab.1 Six-DOF Vibration Model Parameters
以国产某中型商用车为研究对象,其驾驶室与货箱的垂直振动和俯仰振动对平顺性评价影响最大,共四个自由度;路面激励通过前、后车桥垂直振动传至车身,影响整体平顺性,共两个自由度,故建立六自由度振动模型,如图1 所示。图中q1、q2分别为前后轮受到的路面位移激励;x1、x2、x3、x4分别为驾驶室、货箱、前桥和后桥非簧载垂直位移;θ1、θ2分别为驾驶室与货箱的俯仰角位移。根据牛顿第二定律,对各质量取隔离体可得式(1)的微分方程组。
2.2 六自由度仿真模型
作为汽车行驶时最主要的激励源,路面激励获取对汽车平顺性分析至关重要,根据文献[8]的研究,通过式(2)的方程获得路面时域激励。
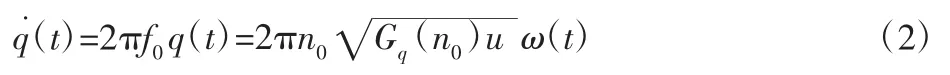
其中:空间下截止频率 f0=u×nq,u 为车速,nq=0.01m-1;q(t)为路面激励;空间参考频率n0=0.1m-1;Gq(n0)=256×10-6m3,为C 级路面不平度系数;ω(t)为功率强度为0.5 的白噪声。根据式(2)建立路面激励模型,设置相应参数后可得图2 所示的仿真路面激励时域曲线。为便于参数设置,将求解模块封装,综合仿真模型,如图3 所示。
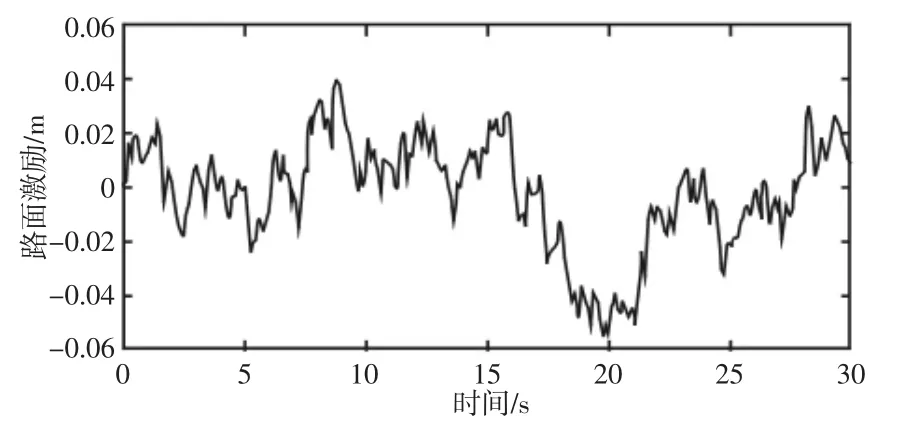
图2 路面激励时域曲线Fig.2 Road Surface Excitation Time Domain Curve
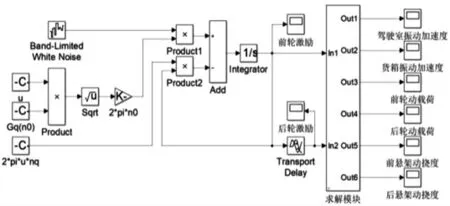
图3 六自由度振动仿真模型Fig.3 Six-DOF Vibration Simulation Model
3 平顺性优化实现与分析
3.1 优化变量与约束条件
由图1 及微分方程可知,车辆力学参数、质量参数和几何参数同平顺性之间具有复杂的非线性关系,共同影响汽车平顺性,全部考虑则不利于优化实现;对于汽车平顺性而言,悬架刚度与阻尼的特性参数对其影响最大。因此选取前、后悬架刚度及阻尼作为优化变量,并将优化变量写成方程形式,如式(3)所示。各优化变量取值范围设为原始值上下波动20%。
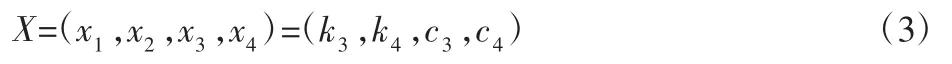
由文献[9-10]可知,为保证汽车正常行驶,需对悬架动挠度、车轮动载荷加以约束,当悬架动挠度均方根值σfd小于1/3 倍许用动挠度[fd]时,可保证悬架撞击限位块的概率小于0.3%,取许用动挠度为0.06m。当车轮相对动载荷均方根值σfd/G小于1/3 时可保证车轮脱离地面的概率小于0.15%,则约束条件可用式(4)表述。

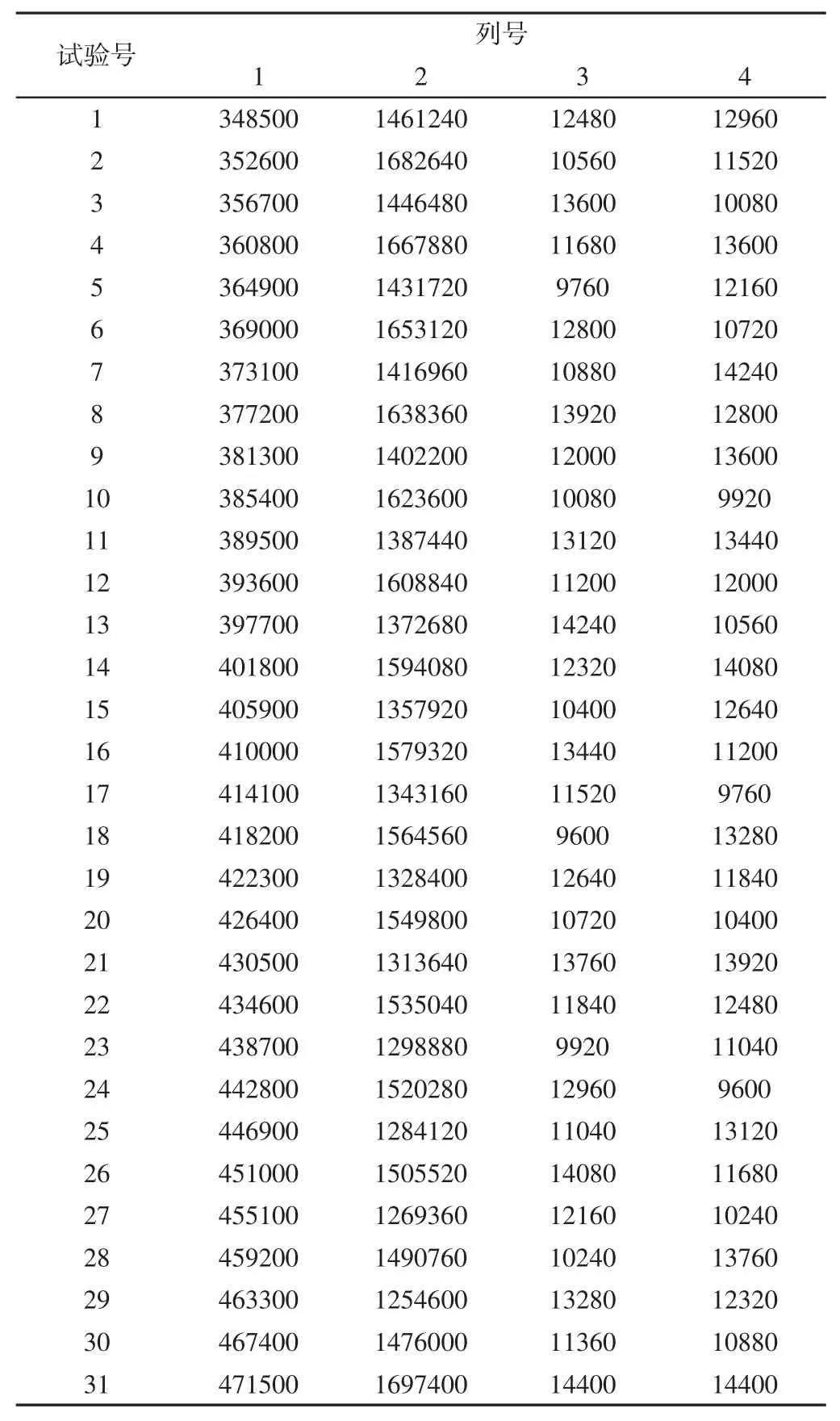
表2 均匀试验设计表Tab.2 Uniform Test Design Table
由于均匀设计法与正交设计法相比,具有试验次数少的优点,特别适合于多因素多水平的试验和系统模型未知的情况。故采用均匀设计法将4 个变量优化区间均匀分为30 个子区间,则因素数为4,水平数为31,均匀试验设计表,如表2 所示。在MATLAB 进行逐步回归,得到的方程,如式(5)所示。

3.2 改进目标函数
根据GB/T 4970—2009《汽车平顺性试验方法》中相关规定,结合引言中的分析,以驾驶室的垂直加速度均方根值代替乘员舒适性,以货箱的垂直加速度均方根值代替货物完好性,选取30、60、90km/h 三种车速为优化的子目标,建立商用车平顺性优化的目标函数:

式中:w1=0.6、w2=0.4—加权系数;AC1RMS1、AC1RMS2、AC1RMS3—30、60、90km/h 时驾驶室加速度均方根值;AC2RMS1、AC2RMS2、AC2RMS3—30、60、90km/h 时货箱加速度均方根值。
3.3 优化结果
鉴于遗传算法在优化应用中具有全局搜索中的优点,采用遗传算法作为对目标车辆进行平顺性优化的工具。优化进程,如图4 所示。从图中可以看出优化算法收敛速度快,迭代到第5 次的时候就基本进入稳定状态,即该优化方法效率高。而优化前后各变量的对比数据,如表3 所示。优化后前悬架刚度降低21.0%,阻尼增加18.6%,后悬架刚度降低8.7%,阻尼增加19.6%。

图4 适应度值历程曲线Fig.4 Fitness Value Evolution Curve

表3 变量优化前后对比Tab.3 Variables Comparison before and after Optimization
4 优化前后平顺性对比
将优化前后变量值带入仿真模型,设置仿真时间为30s,要求优化前后限带白噪声的功率强度和种子设置相同。得到目标车辆在C 级路面分别以30、60、90km/h 行驶时驾驶室、货箱垂直振动的时域图与功率谱密度图,如图5、图6 所示。

图5 优化前后驾驶室加速度对比Fig.5 Comparison of Cab Acceleration before and after Optimization
从图5 和图6 可知,驾驶室与货箱振动的加速度与功率谱密度随车速的增加而增加,即平顺性随车速的增加而变差。由图5 和图6 计算可得优化前后振动峰值对比,如表4 所示。对比分析可知优化后目标车辆平顺性较优化前有明显提高。时域峰值中驾驶室振动至少降低14.2%,货箱至少降低30.9%,而功率谱峰值中驾驶室振动至少降低25.1%,货箱至少降低48.3%,理想的完成了对商用车平顺性优化的目标。同时货箱振动变化为驾驶室振动变化的两倍,即悬架参数改变对货箱振动的影响远大于对驾驶室振动的影响。
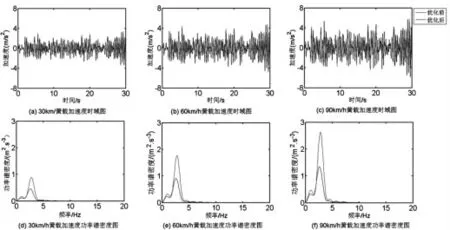
图6 优化前后货箱加速度对比Fig.6 Comparison of Goods Container Acceleration before and after Optimization

表4 优化前后振动峰值对比Tab.4 Comparison of Vibration Peak Values before and after Optimization
5 结论
在建立商用车6 自由度振动仿真模型的基础上,对平顺性优化方法与平顺性响应对悬架参数改变进行研究,基于遗传算法获得可行域内前后悬架刚度及阻尼最优值,并对比优化前后不同车速下不同位置的平顺性结果,得出如下结论:
(1)以驾驶室振动加速度、货箱振动加速度为优化指标。3 种车速下驾驶室振动时域峰值最高降低17.7%、功率谱密度最大降低25.4%;货箱振动时域峰值最高降低31.4%、功率谱密度峰值最高降低48.7%。实现了目标车辆平顺性优化,达到了提高乘坐舒适性和货物安全性的目的。
(2)优化仅经过了5 次迭代就接近最优值,避免了传统优化算法复杂、耗时长和精度低的缺点,表明提出的优化处理方法对使用MATLAB 对汽车平顺性进行优化汽车振动优化具有良好的可行性,适合于悬架动挠度、车轮动载荷等约束问题的求解。
(3)货物安全性改变较乘员舒适性改变将近两倍,即悬架参数改变对货物安全性的影响远大于对乘坐舒适性的影响,为不影响整体平顺性效果,商用车平顺性优化时对货箱振动加以考虑十分必要。

