四腿菱形变截面梁微加速度计结构设计与研究
韩建男,孙江宏,鹿昆磊
(北京信息科技大学机电工程学院,北京 100192)
1 引言
变极距式电容传感器是硅微加速度传感器的一种,由于其结构简单、动态响应好、灵敏度高及便利的操作接口[1-2],自面世以来一直作为最重要的惯性仪器之一,被广泛应用于国防、航天等部门,是惯性导航和惯性制导系统中不可缺少的一部分。
在硅微加速度计中,多数采用等截面梁结构,但其应力集中引起的结构损坏容易导致器件失效[3-4],通常采用截面根部增加适当的圆角、倒角过渡的方法来减小应力集中。随着近年来对变截面梁研究逐步增多,以及微纳机械制造工艺日渐成熟[5-7],开始逐渐采用变截面梁来增大连接处的过渡角[8]的方法消除和降低应力集中。目前对变截面梁结构系统有了一系列的研究,根据矩阵结构分析和弹性力学理论,苑伟政和郝星建立线性变截面梁的力学模型[9];根据材料力学理论,文献[10]建立了变截面梁弯曲数学模型;在微加速度计等截面梁的基础上,文献[11]设计并优化了一种梯形变截面梁;在保证传感器外形尺寸不变的基础上,文献[12]建立了基于槽型变截面弹性梁的传感器灵敏度分析模型,分析了影响灵敏度的关键设计因素;但采用不同截面形状的梁结构,其性能都不一样。
这里设计的是菱形变截面梁结构,菱形变截面增大连接处的过渡角,减小了应力集中,使检测方向与非检测方向刚度最大化,增加了系统的稳定性。在体积和非检测方向刚度相同的条件下,菱形变截面梁与等截面相比,危险截面处最大应力相当而检测方向刚度减小,系统灵敏度大大提高,且在保证静电力刚度小于机械刚度的前提下,可以确定菱形变截面梁加速度计的最大量程。
2 加速度计的工作原理
电容微加速度计的加速度值不容易直接被测量,当物体受到加速度时,会产生惯性力,所以现在都是采用先测量物体的惯性力,再通过公式:

间接测量出加速度的值,然后对加速度再进行两次积分就可以得到物体的空间位置。
加速度计的结构简图,如图1 所示。一般加速度计常通过4个梁将其固接于被测物体上,质量块两侧各两个对称梁,增加了系统的稳定性。检测质量块通过挠性梁与固定端硅基底相连,垂直悬在基底上方。充当检测电极的极板被等间距地固定在检测质量块的上下两面,与检测质量块形成差动电容。

图1 菱形变截面梁加速度计结构简图Fig.1 The Structure Diagram of Micro-Accelerometer Based on Rhombic Variable Cross-Section Beam
变间距型电容式微机械加速度计的平面示意图,如图2 所示。一共有三块平行极板,两块为固定极板,一块为可动极板,且两固定极板与中间可动极板之间的初始距离为d0,相对有效面积都为A,介质介电常数为ε。在物体还未运动时,可动极板与两固定极板分别形成两个电容C1和C2,大小与静态电容C0相等,(C0=εA/d0)。当可动极板受到一个向右的加速度时,这时就会产生一个向左的位移x,于是两个电容的极板间距发生变化,从而引起差动电容的变化。

图2 变间距型电容式微机械加速度计工作原理图Fig.2 The Working Principle Figure of the Variable Distance Capacitance Sensor Micro-Accelerometer

通过泰勒展开得:

因此,形成的差动电容为:

由于敏感质量块受到惯性力产生的位移x< 由上可知,在忽略高阶项之后,差动电容C 与位移成正比,敏感质量的位移信号可以转化为差动电容的电容变化。 加速度计的动力学模型相当于一个弹簧-质量-阻尼系统,如图3 所示。敏感质量块在惯性力运动过程中,会受到空气的阻尼力,阻尼系数为c。加速度计的四个弹性梁相当于弹簧,刚度系数为k。在质量块受到一个加速度a 时,质量块会产生一个与惯性力F 相反方向的位移x,支撑梁发生弹性弯曲,生成弹性力Fk,方向与位移相反。当弹性力Fk与惯性力F 相等时,整个系统达到平衡状态。从而由力平衡方程F=Fk得出质量块移动的位移为: 图3 加速度计经典动力学模型Fig.3 The Classic Dynamic Model of Accelerometer 由牛顿第二定律可得加速度计的二阶动态微分方程为: 对式(8)进行Laplace 变换,得到传递函数为: 当系统达到平衡状态时,由式(8)可得到质量块产生位移为: 通过式(10)和式(7)可以计算出质量块的加速度a。定义加速度计的灵敏度sc为: 从式(11)可以看出,灵敏度sc和系统的固有频率、质量块m、刚度系数k 有关系,固有频率越低,灵敏度越高。要想增大系统灵敏度,可以通过降低系统的刚度系数k 和增大质量块m 的质量,但又不能使刚度系数k 过低,过低又会导致整个系统不稳定。 图4 菱形变截面梁结构Fig.4 The Structure of Rhombic Variable Cross-Section Beam 菱形变截面梁的结构,如图4 所示。Y 轴为梁检测方向,其倾角为β;Z 轴为梁非检测方向,其倾角为α;左端横截面的短轴和长轴长度分别为b1和a1,左端横截面相连于质量块,右侧的横截面为固定端。 要使Z 轴刚度与Y 轴刚度相差越大,则a、b 的尺寸相差就越大,所以不妨 a1=8μm,tanβ=0.05,b1=2μm。在梁的实际结构中,截面尺寸都是远小于变截面梁长度的,所以可以忽略剪切力的影响,只考虑变截面梁的纯弯曲力学模型,截面尺寸随长度线性变化,距离坐标原点x 处菱形截面的长轴长ax和短轴长bx分别为: 式中:E—梁弹性模量;M(x)—梁受到的弯矩;I(x)—梁截面惯性矩;w—梁挠度。 当在Z 轴上有加速度时,距原点x 处横截面对Y 轴惯性矩Iy和力矩 M(x)分别为 将式(14)和式(15)代入式(13)并对 x 进行积分得转角 φ 为: 再次对x 变量积分得挠度w: 当x=0 时,挠度w 取最大值为: 当F、wmax固定不变时,根据式(18)定义变截面梁刚度为KZ为: 式(19)的图像,如图5 所示。梁Z 轴刚度随梁跨度l 减小而增大,随截面高度a2增加而增加,当梁长度l 在100μm 到250μm范围内,梁末端高度 a2增加到 30μm 到 60μm 之间,Z 轴刚度变化不大。 图5 菱形变截面梁z 轴刚度与梁尺寸关系Fig.5 Relationship Between z Axis Stiffness and Size of Rhombic Variable Cross-Section Beam 当在Y 轴上有加速度时,刚度分析同前文相同,距原点x 处横截面对Z 轴的惯性矩为: 转角为: 再次对x 变量积分得挠度w: 当 x=0 时,Y 轴的最大挠度 wmax为: 由式(23)可得 Y 轴刚度 KY为: 式(24)的图像,如图6 所示。Y 轴刚度随梁跨度l 减小而增大,随梁末端长轴 a2增大而增大。当 l 在 100μm 到 150μm 范围内,且 a2在 35μm 到 60μm 之间时,Y 轴刚度变化不大。 图6 菱形变截面梁Y 轴刚度与梁尺寸关系Fig.6 Relationship Between Y Axis Stiffness and Size of Rhombic Variable Cross-Section Beam 由于Iy>Iz,所以在加速度一定时必须满足Y 轴强度要求。Y轴方向作用加速度时,由材料力学可知,距离原点x 处截面的Y轴最大弯曲应力为: 将式(14)代入式(26)得: 求导得: 图7 菱形变截面梁Y 轴最大应力σ′(x)Fig.7 Maximum Stress σ′(x)of Y Axis of Rhombic Variable Cross-Section Beam 为增加系统的稳定性,就要减小Y 轴方向的刚度,使Y 轴的灵敏性提高,增大Z 轴方向的刚度,使Z 轴方向的灵敏性降低。同时为使整个系统工作稳定,还应防止因产生过大的静电力,而导致极板吸合,所以系统机械刚度必须要大于静电刚度[13]。 在反馈电压的作用下,可动梳齿电极上受到的静电力为Fe: 所以可得到的静电刚度为: 由此静电刚度ke的变化范围为: 如果Y 轴方向上的梁的刚度k 小于静电力产生的静电刚度ke,那么系统将失去平衡,处于不稳定状态,因此: 式中:ε—空气介电常数;A—两极板正对面积;ke—系统静电刚度;k—系统Y 轴机械刚度;Fe—质量块受到的静电力;Vvef—施加在两边固定梳齿电极上的参考电压;Vout—输出电压。 对比图5 和图6 可知,菱形变截面梁Z 轴刚度大约是Y 轴刚度的16.8 倍,能较好地减小对Y 轴的干扰影响。菱形变截面梁能减小应力集中的影响,提高系统的稳定性。 根据输入加速度与双边电容变化关系,可以得出电容差值量C 与加速度a 之间的关系式为: 不同加速度会产生不同的电容变化,所以只需测出电路中电容的变化,就可以求得加速度的大小。变间距型电容式加速度计的灵敏度Sc为: 由此可见,可以利用增大静态电容C0和敏感质量块的质量,减小初始极板间隙d0和加速度计的刚度系数k 的方法来提高加速度计的灵敏度。 对于闭环反馈式梳齿微机械加速度计的量程分析。当加速度计正常工作时,质量块产生的惯性力与反馈电压产生的静电合力相平衡,系统处于平衡稳定状态。由式(30)可得静电合力为: 质量块产生的惯性力为:F=ma 所以可得加速度的最大值amax为: 一般说来,在结构尺寸确定的情况下,提高加速度计的量程也就只能增加参考电压。但参考电压不可能无限制增大,还需要满足稳定性要求。所以在满足稳定性即机械刚度大于静电力刚度的条件下,可算出最大加速度amax。 在满足强度要求下,要适当减小Y 轴刚度k,提高系统灵敏度,但又不能过小,否则会使系统固有频率过低。从稳定性方面分析,主要考虑Y 轴方向的刚度,选取Y 轴刚度为最大值时的尺寸,而此时梁Z 轴的刚度为Y 轴刚度的16.7 倍,能很好的减少Z轴方向刚度对Y 轴方向检测的影响,且Y 轴方向能够检测到更大的量程。菱形变截面梁尺寸,如表1 所示。当a、b 均为常数时,梁为等截面梁,当其满足下列等式时,可计算出等截面梁的尺寸: 表1 两种加速度计梁尺寸参数Tab.1 The Parameters of Two Kinds of Accelerometer Beams 经计算可得,等截面梁的Y 轴和Z 轴刚度分别为2.9234×10-3N/μm、0.02183N/μm。椭圆形变截面梁 Y 轴 Z 轴刚度分别为1.2998×10-3N/μm、0.02183N/μm。 系统总质量由质量块、梳齿的质量和梁的质量构成。因为质量块和梳齿的质量是一定的,且等截面与变截面的体积相等。所以可得等截面梁加速度计与梯形变截面梁加速度计的总质量关系为:m变梁=m等梁 菱形变截面梁加速度计与等截面梁加速度计的固有频率关系为:ωn变=0.66ωn等 由图7 和计算等截面梁加速度计梁的强度可得两者的关系为: σmax变=1.2σmax等 由式(11)可得菱形变截面梁加速度计与等截面梁加速度计的灵敏度关系为:Sc变=2.25Sc等 由式(38)可计算变截面加速度计的最大量程为: 在等截面梁和变截面梁的质量相同且Z 轴同等刚度条件下,菱形变截面梁与等截面梁相比,危险截面处应力仅增加20%,而菱形变截面梁检测方向刚度却是等截面梁的0.44 倍,系统灵敏度是其等截面的2.25 倍,且能达到的最大加速度量程为668.8g。 菱形变截面梁能减小梁的应力集中,可使加速度计检测方向和非检测方向刚度的区分度达到最大,减小非检测方向对检测方向灵敏度的影响,提高了系统的稳定性。在梁质量相等和非检测方向刚度相同的条件下,菱形变截面梁与等截面梁相比,危险截面处应力相当而检测方向刚度减小,系统灵敏度大大提高,同时梁的量程能达到668.8g。
3 加速度计的力学模型






4 菱形变截面梁力学模型建立


4.1 Z 轴刚度







4.2 Y 轴刚度分析






4.3 梁的强度分析


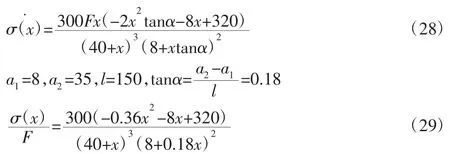

5 系统性能分析与量程
5.1 系统稳定性分析




5.2 系统的灵敏度


5.3 系统的量程


5.4 变截面梁的参数优化




6 结论

