伺服压力机模糊智能控制算法研究

何彦忠，王兴松，陈 静

（1．东南大学 机械工程学院，江苏 南京 211189；2．力信（江苏）能源科技有限责任公司，江苏 镇江 212132）

自从美国数学家维纳于20世纪40年代创立控制论以来，自动控制理论经历了经典控制理论和现代控制理论两个重要发展阶段。在处理复杂系统控制问题时，传统的控制理论对于复杂性所带来的问题总是力图突破旧的模式以适应社会对自动化提出的新要求。世界各国控制理论界也都在探索建立新一代的控制理论，以解决复杂系统的控制问题。近年来，把传统控制理论与模糊逻辑神经网络遗传算法等人工智能技术相结合，充分利用人类的控制知识对复杂系统进行控制，逐渐形成了智能控制理论的雏形。

1985年，IEEE在纽约召开了第一届智能控制学术会议，集中讨论智能控制的原理和系统结构等问题，标志着这一新的体系的形成。虽然智能控制体系的形成只有三十几年的历史，理论还远未成熟，但已有的应用成果和理论发展都表明智能控制正成为自动控制的前沿学科之一。概括地说，智能控制具有以下基本特点：

（1）应能对复杂系统（如非线性、快时变、复杂多变量、环境扰动等）进行有效的全局控制，并具有较强的容错能力；

（2）定性决策和变量控制相结合的多模态组合控制；

（3）其基本目的是从系统的功能和整体优化的角度来分析和综合系统，以实现预定的目标，并应具有自组织能力；

（4）同时具有以知识表示的非数学广义模型和以数学模型表示的混合控制过程，人的知识在控制中起着重要的协调作用，系统在信息处理上既有数学运算，又有逻辑和知识推理。

模糊控制是一类智能控制的形式。现代计算机虽然有着极高的计算速度和极大的存储能力，但却不能完成一些人看起来很简单的任务。一个很重要的原因是模糊决策和推理的能力，模糊控制正是试图模仿人的这种功能。

随着现代制造业的发展，塑性加工、粉末成形、难成形材料成形、复杂形状零件成形、复合成形以及高精度成形等的需求日益强烈[1]。在“绿色制造”（Green Manufacturing）的概念已成为制造业可持续发展的主要趋势的今天[2]，传统压力机的性能已不能满足变革中成形工艺的要求。为此，出现了伺服压力机，其在汽车零件、电子零件等高精度、难成形零件加工领域中，有着广泛的应用前景[3-5]。伺服压力机主要用于拉深、冲裁、弯曲和冷锻等生产线及试模压力机[6]。采用数控技术，可控制滑块行程和加工曲线以提高加工效率；在进行反馈控制后系统精度得到大幅提高；还可对滑块的输出力和运动轨迹进行控制；这不但更节能[7-8]；而且改善了压力机的工作环境，降低了振动和噪声[9]，为拓展新的成形加工工艺和模具制造方法提供了广阔前景。

随着科技的发展，伺服电机的控制方式也更加先进、高效、精确，日渐向智能化方向发展[10-11]。研究表明，采用自适应控制技术，利用伺服电机驱动曲柄滑块机构，通过计算机数字控制系统控制伺服电机，可以进一步精确地控制压力机滑块的位置和速度，满足生产加工工艺对滑块运动曲线的要求[4,12-13]。在实际生产中将会获得很大的社会效益和经济效益，体现绿色制造中的节能、降噪的先进思想[14]。

智能压力机是具有感知、决策、执行功能的压力机装备，由开关磁阻伺服电机驱动装备的工作机构，由计算机进行整机控制。开关磁阻伺服电机通过角位移传感器和电流传感器的感知，对运动和压力进行智能数控。智能压力机的组成是开关磁阻伺服电机驱动主运动，计算机PLC、触摸屏通过网络连接伺服电机控制器，连接互联网。

1 智能压力机硬件系统

伺服压力机，主要由机械系统、伺服驱动系统、控制系统、反馈系统组成，可通过直接驱动曲柄连杆机构来控制滑块行程[4]。图1所示为实验用伺服压力机，其由伺服电机驱动系统和曲柄压力机构成。

图1 伺服压力机

如图2所示，系统采用MCX314运动控制卡、PCL-818控制卡等组成一反馈控制系统。

2 模糊PID控制器的设计

图2 控制系统框图

模糊控制器是模糊控制系统的核心，其性能的优劣，主要取决于模糊控制器的结构、模糊规则、合成推理算法，以及模糊决策方法等因素，应总结工程设计人员的技术知识和操作经验，从稳定性、响应速度、超调量和稳定精度等各方面来考虑。

2.1 确定模糊控制器的结构

如图3所示，根据控制要求，模糊控制器采用二输入三输出的形式。

图3 伺服控制系统框图

采用位置偏差E和位置偏差变化率Ec作为模糊算法的输入变量，PID控制器的三个参数KP，KI，KD作为输出。利用模糊规则进行模糊推理，查询模糊规则表进行参数调整。输出变量为PID参数KP，KI，KD。

2.2 论域及相关参数的确定

隶属度函数采用Z形、S曲线形和三角形隶属度函数。根据模糊控制的基本原理与本系统的特性将E和Ec的论域定义为[-1,1]。E的隶属关系如图4所示。

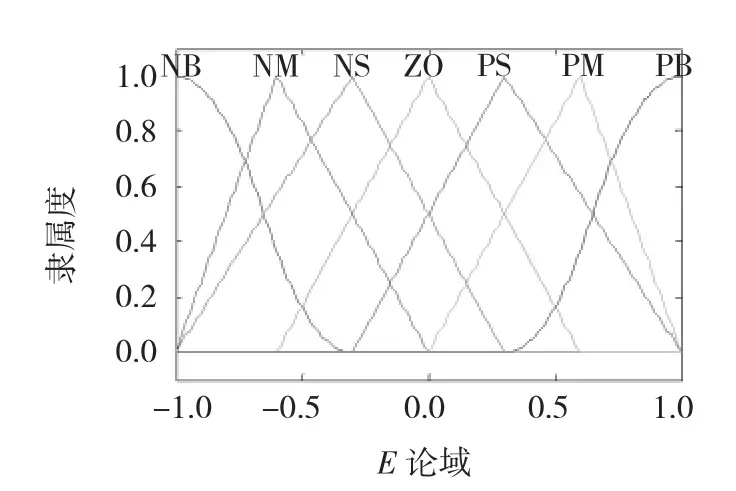
图4 的隶属度函数

2.3 参数调整原则及模糊规则的建立

模糊控制设计的核心是根据已有技术知识和实际操作经验[15-17]，结合位置误差和误差变化率的大中小各种状态，建立合适的模糊控制规则表。比例系数KP的作用是加快系统的响应速度，比例控制器的输出与输入误差信号成比例关系。积分系数KI的作用是消除系统的稳态误差，积分控制器的输出与输入误差信号的积分成正比关系。微分系数KD的作用是改善系统的动态性能，微分控制器的输出与输入误差信号的微分成正比关系。

2.4 模糊推理规则

由模糊控制规则整定输出量是一个模糊集合，需将其转换成精确值后输出。采用面积中心法（centroid）根据输出模糊子集的隶属度，计算出输出量的精确值。图5为MATLAB控制工具箱中KP，KI，KD输出曲面图。

图5 KP，KI，KD 输出曲面

3 滑块位置实验研究

3.1 方案实施

伺服压力机实验：在伺服压力机无负载的情况下进行实验，采用伺服电机旋转角度为受控对象。

3.2 阶跃响应实验

在给定阶跃信号为1000脉冲的时候，分别采用模糊PID控制器和线性PID控制器，其阶跃响应曲线如图6所示。

本文中线性PID控制器的控制周期T=0.005s，模糊PID控制器的控制周期T=0.016s。

以上实验分别就线性PID和模糊PID控制进行研究。虽然线性PID具有结构简单，运算量小的特点；而模糊PID结构复杂，运算时间较长。但是如表1所示，对实验结果进行比较，模糊PID控制系统的阶跃响应动态性能明显优于线性PID控制系统。

采用模糊PID参数自整定控制，系统的响应速度加快、调节精度提高、稳态性能变好，具有较强的鲁棒性，抗干扰能力明显优于线性PID控制器。

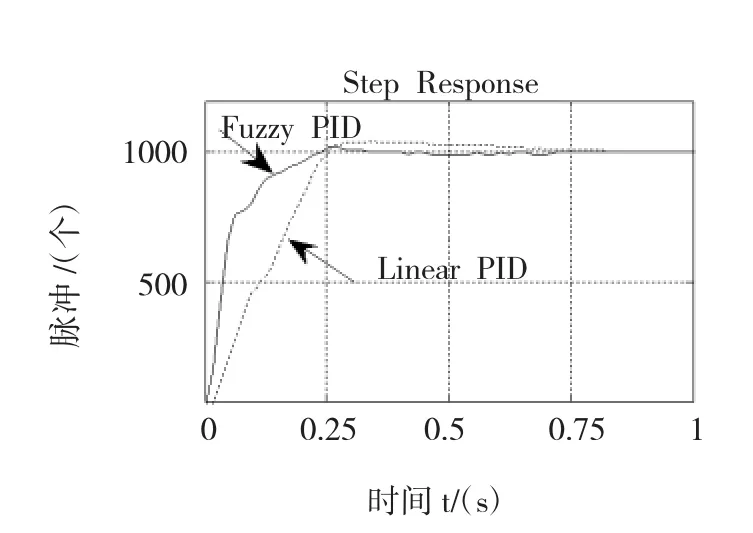
图6 伺服压力机位置控制系统阶跃响应曲线

表1 控制结果比较

3.3 正弦跟随实验

以正弦信号作为控制量，分别采用模糊PID控制器和线性PID控制器进行跟随控制，得到控制伺服系统的实验曲线（图7）。

图7 模糊PID与线性PID控制器正弦信号响应曲线

图8所示为模糊PID与线性PID控制器正弦信号响应误差曲线。可以观察到在系统较为稳定的情况下，线性PID由于结构简单，运算时间较短的优点。但是当控制环境变化的时候模糊PID器整体表现比较稳定，而线性PID控制器整体控制误差较大。

图9为模糊算法得到的PID参数值，可以看到在模糊PID控制器中KP，KI，KD三个参数随着误差量的变化在不停的变化调整，以适应系统的变化。

4 结论

本文在智能控制的框架下，对模糊模型与基本控制算法、非线性系统的模糊建模与控制、模糊预测控制、模糊控制系统的稳定性分析等方面进行了较详细的阐述和分析。

图8 模糊PID与线性PID控制器正弦信号响应误差曲线

图9 模糊PID控制器参数随误差变化曲线

基于模糊PID理论的控制器，其响应快、超调小，较好地解决了线性PID控制中存在的超调量和快速响应之间的矛盾，受系统参数突变的影响比较小，控制精度高，且有较强的鲁棒性，抗干扰能力也较线性PID控制器有所提高。可以用于复杂的控制系统，具有很好的应用前景。