OCP-60E 型机械压力机隔振系统设计
缪海楠,葛 奇,包松东,曹春波,闵文君
(1.金丰(中国)机械工业有限公司,浙江 宁波315211;2.宁波大学 机械工程与力学学院,浙江 宁波315211)
与传统的机加工工艺相比,冲压工艺在生产过程中,不仅节省资源,而且成型率高,因此冲压工艺得到越来越广泛的应用[1]。由于机械压力机的曲柄滑块机构的工作特性,在加工过程中不可避免地会产生振动和噪声,这严重影响了机器的正常使用和工作人员的健康。同时,在精密加工中,对冲压零件的要求更加严格。如果不对压力机的振动进行控制,它将无法达到合格生产的标准。另外,长期的振动和噪声也会加快设备部件的损坏[2]。
在对机械压力机的减振、抑振研究上,LL.Koss[3]最早对压力机的前6 阶振型与阻尼比,提出了压力机模态受自身结构影响。M.Otsu[4]利用数控伺服压力机可编程的特性,通过让滑块在冲裁完成后停顿的方法,来降低压力机工作时的振动。张世顺[5]通过研究压力机反向载荷产生的机理,提出了一种反向载荷控制的方法。这既消除了反向载荷,又降低行程中的加速度。徐腾[6]建立了多领域统一模型,通过设计安装压力机液压子系统以及对滑块机构进行拓扑优化,有效改善压力机振动问题。黄栋[7]设计了一种新型非线性组合隔振器,有限元仿真表明其设计的隔振器优于传统橡胶隔振器。周宇[8]通过优化机构运动参数及对曲轴进行动平衡设计,达到抑振效果。
本文对机械压力机建立了隔振系统力学模型,并对该系统数学模型进行分析计算。分别对比分析了不同机身质量、平台质量、隔振器刚度与阻尼、平台刚度与阻尼对压力机整体和平台的振幅影响。最后建立振动优化数学模型,计算隔振器刚度与阻尼最优值,得到最优的隔振器参数。
1 机械压力机的工作结构
本文以OCP-60E 机械压力机为研究对象进行研究。它的工作原理[9]是通过两次减速(分别为电机转动导致三角皮带引起大带轮减速,大带轮的减速效果经传动轴传到小齿轮引起大齿轮再次减速)。接着带动下方的曲轴旋转,与曲轴刚性连接的连杆引起滑块做上下来回的直线运动,从而产生冲压效果。大齿轮与曲轴之间的离合器、制动器属操纵机构,当离合器与大齿轮啮合时,引起滑块运动;制动器工作时,滑块停止运动,这样便可控制滑块连续或间断运动。大带轮带动飞轮旋转储能,保证电机负荷均匀。
该压力机采用对心式曲柄滑块机构,图1 为该机构的运动简图。其中A、B 均为转动副,A 点为曲轴和连杆的交接处,B 点为连杆和滑块的交接处。O 点为曲柄旋转中心,OA 为曲柄半径,即曲轴旋转中心到曲柄销中心之间的距离,AB 为连杆部分,质量块B 为机械压力机滑块,这三部分构成机械压力机的核心运动部件-曲柄滑块机构。曲柄OA 为驱动端进行旋转,滑块在曲轴OA 的带动下进行上下往复运动。
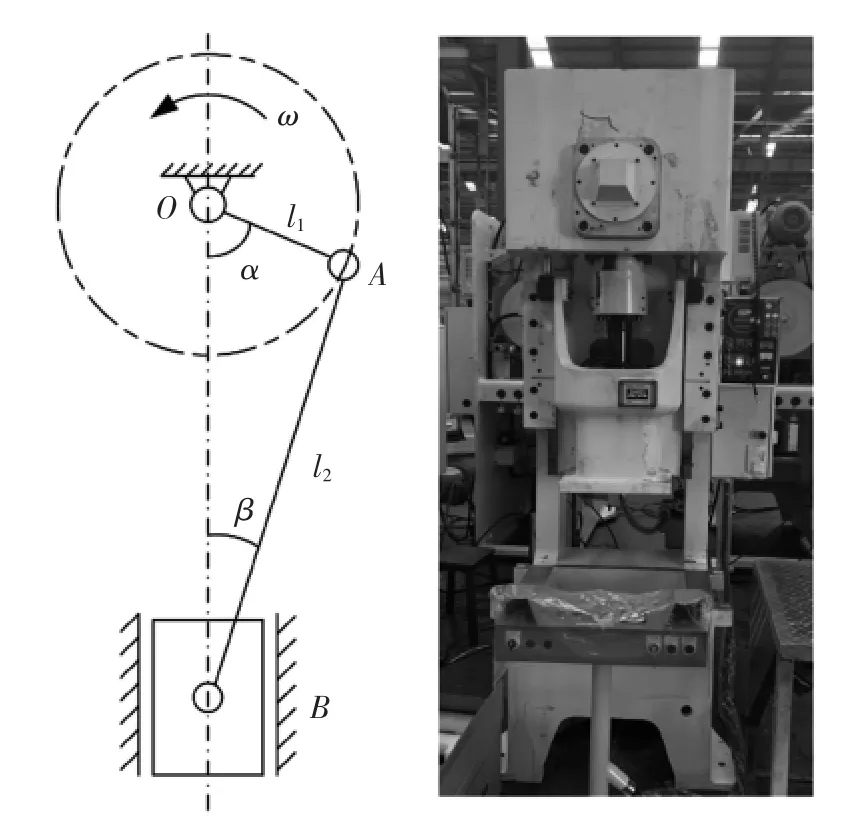
图1 曲柄滑块机构运动简图
2 压力机隔振系统理论模型
2.1 压力机隔振系统力学模型
机械压力机的隔振通常有三种方式[10]:①普通橡胶隔振。橡胶隔振具有质量小,安装和拆卸方便。然而寿命是普通橡胶材料的常见问题,以及材料本身耐油性差,易老化。②空气弹簧指在柔性密闭容器中加入压力空气,利用空气压缩的非线性恢复力来实现隔振和缓冲作用的一种非金属弹簧。它具有非线性硬特性,避免共振,防冲击的特性,能够起到较好的减振作用。但是空气弹簧寿命短,成本高[11]。③金属弹簧隔振。由于其本身阻尼系数小,为了加速消极隔振的自由衰减振动的过程[12]。通常情况与它阻尼大的隔振材料联合使用。具有寿命长,无需维护的优点。由于弹簧阻尼隔振具有性能好、寿命长以及易维护等多方面的明显优势,因此应用在多数机械压力机的隔振系统中。如图2 所示,本文研究的机械压力机,通过在压力机和安装平面之间放置四个隔振器进行隔振。

图2 机械压力机隔振系统图

图3 双自由度有阻尼力学模型
简化模型如图3 所示。在压力机床身底座下安装隔振器时,因压力机机身和安装平面的刚度比隔振器和地面土壤的刚度大得多,所以将压力机和安装平面简化为两个刚性质点[13]。粘性阻尼的系数设定为c1,c2。线性弹簧体的刚度设定为k1,k2。对于整个简化的系统而言,竖直方向的惯性力分量下系统做受迫运动,其中将作用在压力机床身上的力简化成正弦力。通过简化,系统的力学模型为具有两个自由度且有阻尼的振动系统。
2.2 隔振系统的动力学模型建模
在图3 所建立的力学模型中,定义机械压力机在初始的位置时,曲轴转角等于0。在此瞬时,压力机和安装平面的位置分别为假定坐标原点,定义该时刻为初始时刻。机械压力机运转后,曲柄滑块机构中的曲柄转角周期性变化将对机械压力机床身产生等效惯性力。由此推导出隔振系统的运动微分方程:

式中:m1——压力机床身质量;m2——安装平台质量;k1、c1——隔振器的刚度和阻尼;k2、c2——地基的刚度和阻尼。地基的刚度表达式[14]中,α——安装平台埋深对于地基抗压刚度的提高系数;CZ——地基抗压刚度系数,S——安装平台底面积。地基阻尼系数表达式中,DZ——地基土壤阻尼比;B——安装平台埋深对垂直方向阻尼比的提高系数。
式(1)的矩阵形式如下:
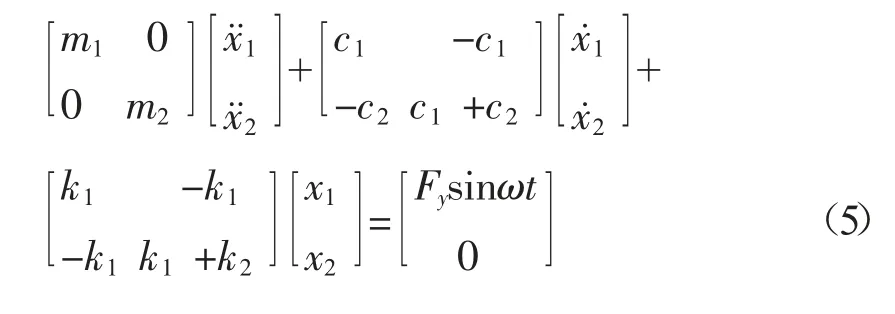
3 压力机隔振系统仿真分析
3.1 数值仿真及优化
根据上述建立的隔振系统的运动方程,采用MATLAB 仿真技术,对隔振系统仿真分析。分别对机械压力机质量、安装平台质量、隔振器刚度与阻尼、地基刚度与阻尼对压力机和平台振幅影响进行分析。
本文采用四阶龙格- 库塔法来解常微分方程,即用四个点处的斜率加权平均作为平均斜率的近似值,构成一系列四阶龙格- 库塔公式。先将式(1)进行降阶处理,新的状态变量变换如下:

因此,式(1)可变换为:
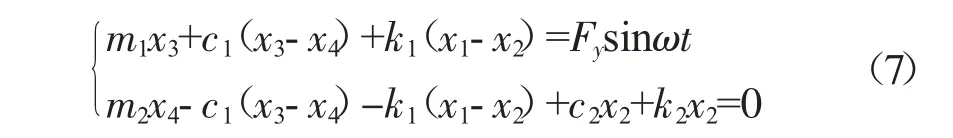
综上,可以得到该运动方程的一阶微分方程组。在MATLAB 中对该微分方程组进行编程计算,根据自定义的初始条件,得到该方程的解,求出该系统在惯性力作用下的时域响应。

由图2 中的隔振系统数学模型可以得到,压力机本身的质量m1,安装平台质量m2,隔振器的阻尼c1和刚度k1,地基的阻尼c2和刚度k2都会对压力机的振幅产生影响。利用MATLAB 进行编程,基于运动方程,对各个影响参数对振动的影响进行仿真分析。该模型系统利用ODE45 解出:

设置隔振系统初始件条如下:x1(0)=0,x2(0)=0,x˙1(0)=0,x˙2(0)=0,时间范围是t=0~0.4。
如下命令进行开始求解:

机械压力机隔振系统相关物理参数如下:整机质量m1=4200kg,平台质量m2=10800kg,隔振器刚度k1=1.17×107N/m,隔振器阻尼c1=2.05×105Ns/m,地基刚度k2=3.18×108N/m,地基阻尼c2=3.16×106Ns/m。通过MATLAB 软件对隔振系统进行仿真计算分析,改变参数变量,分析其对压力机振幅和安装平台振幅的影响。
3.2 仿真分析
图4 为压力机整体质量对压力机振幅与平台振幅的影响。压力机质量改变,引起平台振动变化规律与引起自身振动的变化规律相同。在2000kg~8000 kg 范围内,随着机身质量的增加,压力机本身和平台的最大振幅都逐渐增大。当压力机整机质量为8000 kg 时,受等效惯性力Fy的影响,通过仿真数据可以知道压力机本身最大振幅为43.99μm。与平台振幅受压力机质量的影响相比,压力机振幅受压力机整体质量的影响更大。在压力机质量的改下下,平台的最大振幅变化范围仅为1.66μm。
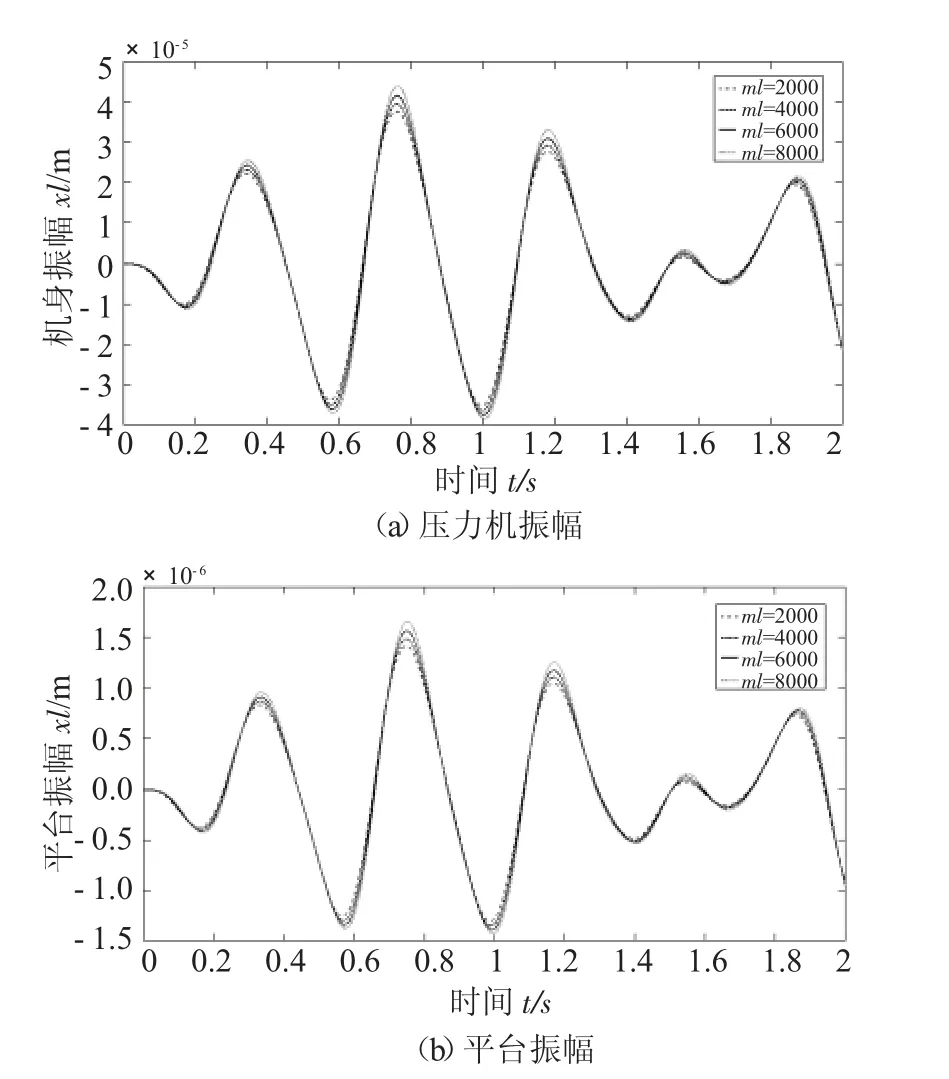
图4 压力机整体质量对振幅的影响
图5 为摆放平台质量对压力机振幅与平台振幅的影响曲线。当摆放平台质量为单一变量发生变化时,可以发现平台质量变化对压力机振幅影响变化较小。通过局部放大我们可以得知,压力机振幅随着摆放平台质量增大而增大,但变化范围很小。m2为200000kg 时最大振幅为40.12μm,与5000kg 最大振幅差值为39μm。摆放平台质量对平台本身影响变化规律也与压力机振幅变化规律类似。m2为200000kg 时最大振幅为1.84μm,与5000kg 最大振幅相差值为3.55μm。综合以上数据可以得知,改变平台质量对压力机振幅和本来自身振幅影响幅度不大,改变平台质量,压力机振幅所受影响要大于平台振幅。
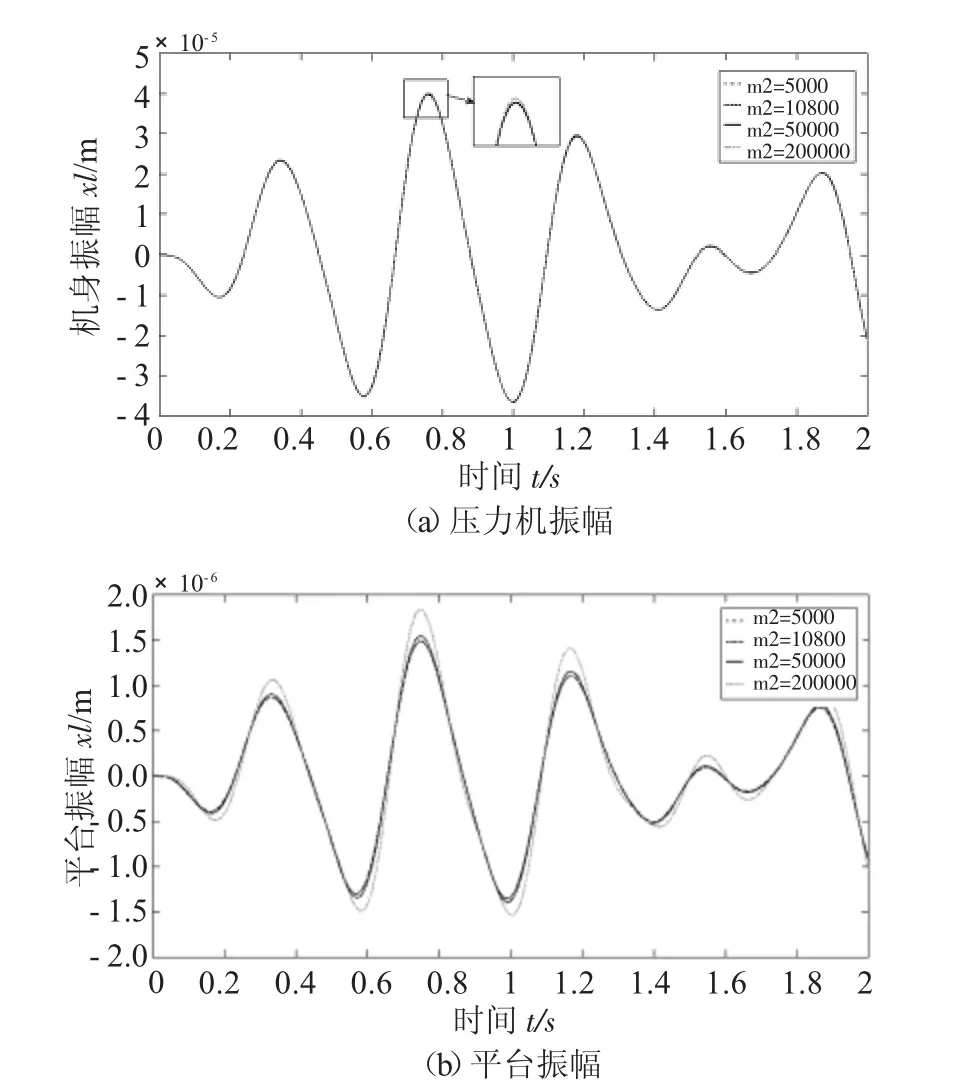
图5 摆放平台质量对振幅的影响
通过观察图6 可知,隔振器刚度变化对压力机振幅影响较大,曲线幅值范围随着隔振器的刚度增加而减小。当k1为1.17×106N/m 时,压力机振幅最大,幅值为108.9μm,此时随着隔振器的刚度增加,压力机振幅变化范围减小。隔振器刚度为k1=1.72×107N/m 时,压力机振幅最大值为39.74μm。隔振器刚度变化对平台振幅的影响较小,最大值为1.49 μm,不同隔振刚度下,最大值差值为1.71μm。综上可知隔振器刚度对压力机振幅影响较大,对平台振动变化影响较小。

图6 隔振器刚度对振幅的影响
通过改变隔振器阻尼大小,计算得出其对压力机振幅和平台的影响。如图7a 所示,随着隔振器阻尼增大,压力机的振幅逐渐变小。隔振器阻尼c1=2.57×103Ns/m 时,最大振幅为42.68μm。隔振器阻尼c1=2.57×106Ns/m 时,最大振幅为10.99μm。振动衰减时间同样随隔振器阻尼的增大而减小。由图7b可以看出随着阻尼的增大,平台的最大振幅逐渐减小。隔振器阻尼c1=2.57×103Ns/m 时,最大振幅为1.502 μm。隔振器阻尼c1=2.57×106Ns/m 时,最大振幅为1.367μm。综上,可知隔振器阻尼对压力机振幅影响较大,对平台振动变化影响较小。
通过观察图8a 可知,地基刚度变化对压力机振幅影响较小。四条曲线中,k2=3.18×107N/m 时,压力机振幅最大,幅值为44.6μm,k2=3.18×109N/m时,压力机振幅最小,幅值为38.27μm。不同隔振刚度下,最大值差值为6.33μm。图8b 中可得地基刚度变化对平台振幅的影响较大,最大值为9.07μm,此时k2=3.18×106N/m。最小值为0.15μm,此时k2=3.18×109N/m。综上分析,可知隔振器刚度对平台振动振幅影响较大,对压力机振幅影响较小。
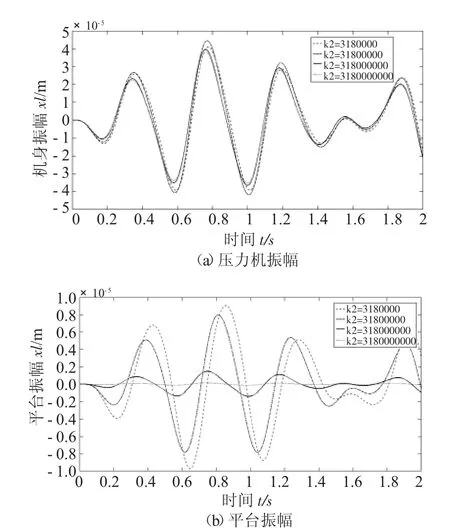
图8 地基刚度对振幅的影响
图9a 为不同地基阻尼对压力机振幅的影响曲线,分析发现地基刚度变化对压力机振幅影响较小。c2=3.25×106Ns/m 时,压力机振幅最大,幅值为39.74 μm,c2=3.25×107Ns/m 时,压力机振幅最小,幅值为38.73μm。不同地基阻尼下,最大值差值为1.01 μm。图9b 为不同地基阻尼对平台振幅的影响曲线。与压力机振幅相比,地基阻尼变化对平台振幅的影响较大,最大值为1.53μm,此时c2=3.25×104Ns/m。最小值为0.78μm,此时c2=3.25×107Ns/m。综上分析,可以得知地基阻尼对平台振动振幅影响较大,对压力机振幅影响较小。地基阻尼对压力机振幅的影响同地基刚度对压力机振幅的影响相似,通过改变地基阻尼和刚度无法实现压力机振幅较大幅度减小。

图9 地基阻尼对振幅的影响
综上,可以得出以下结论:
(1)压力机质量对压力机自身及平台振幅影响较小,若通过改变压力机自身质量达到减小压力机自身和平台的振幅较难实现。实际情况,压力机本身机构设计已经较为完善,不易大幅度改变质量,因此从实际上来考虑压力机的减振情况因从其他影响参数取改善。
(2)通过分析可以发现改变隔振器刚度和阻尼能够有效的改善压力机的振幅,改变地基的阻尼和刚度对压力机振幅影响较小,但是可以通过改变地基的阻尼和刚度来实现改善平台的振幅。
4 压力机隔振系统参数优化
通过上述分析可知,在隔振系统中,隔振器的刚度和阻尼对压力机振动影响效果最大。合理的刚度值和阻尼值能够有效的解决压力机的振动问题。通过设计优化的思想,将压力机自身振动加速度在求解区间的最大值x1mn为目标函数,隔振器刚度k1、隔振器阻尼c1为设计变量,在约束条件下,求解目标函数最小值。
为了便于求解,压力机整体的最大振幅为x1max目标函数,优化参数选择隔振器的刚度k1和隔振器阻尼c1。约束条件为压力机的某一要求振动幅值临界值。由下式可以求出压力机整体振幅和安装平台振幅的最大值。

将隔振器刚度k1、隔振器阻尼c1求解优化问题转化为如下优化问题的表达式形式:

式中:[x1m]为压力机和平台限定的最大位移值。
利用MATLAB 软件中的优化函数[15]可以进行求解计算。设计时机身的最大位移[x1m]=0.02mm,优化前后的仿真结果对比如表1 所示。优化前后压力机的振幅随时间变化曲线如图10 所示。优化前最大振幅39.74μm,优化后最大振幅19.95μm。减少了19.79μm,比优化前减少了49.79%,平台最大振幅由1.49 μm 减少为1.23μm,减少了0.26μm。

表1 优化方案与原方案对比

图10 优化前后压力机的振幅曲线
5 结论
针对机械压力机振动问题,本文以OCP-60E 型机械压力机作为研究对象,对其隔振系统的进行了分析,得到了该机械压力机的减振与抑振方法。
建立了机械压力机振动力学模型,将机械压力机和安装平台视为两个刚性质量,机械压力机地脚的隔振器和安装平台的地基整体视为线性弹性体与粘性阻尼,建立振动系统理论模型,模型简化变为一个双自由度有阻尼力学模型。通过控制单一变量的方法,分析不同压力机质量、安装平台质量、隔振器刚度与阻尼、地基的刚度和阻尼对压力机和平台振幅影响。通过MATLAB 进行数值仿真,得到各组数据和曲线。最后利用优化工具对影响压力机振幅最大的隔振器刚度和阻尼参数进行优化设计,得到最优的隔振器参数,优化后振幅减少了49.79%,减振效果明显。

