地铁交流牵引供电设备时变故障率分析

王 平，陈 霞，金 辉，杨茜茜，林 圣

(1.广州地铁集团有限公司，广州 510000；2.广州地铁设计研究院有限公司，广州 510000；3.西南交通大学 电气工程学院，成都 610031)

设备故障率是牵引供电系统可靠性评估中必要的基础数据，由于存在牵引供电设备的故障记录等基础数据缺失的状况[1]，在可靠性评估中一般假定牵引供电设备故障率恒定不变.因此，为地铁交流牵引变电所可靠性评估提供数据支撑和条件保证，减少因故障率带来的可靠性评估误差，对牵引供电设备故障率的时变特性进行研究是非常必要的.

对地铁交流牵引供电设备故障率模型进行建模分析与求解，分析牵引供电设备故障率的时变特性，主要需要考虑两个方面：一是部分关键供电设备存在故障数据缺失情况，如何充分利用现有数据对缺失故障数据的设备进行可靠性评估；二是影响供电设备故障率的不确定性因素复杂.如何在可靠性评估中体现这些不确定性因素,基于此，专家学者开展了以下研究：在故障率模型建立方面，文献[2-3]采用分段多项式对设备的寿命参数进行了拟合评估，并对其故障率特性进行了简略分析，但由于故障数据偏少，导致模型精度较低；文献[4-5]采用三参数威布尔函数作为设备的寿命分布模型，一定程度上提高了模型精度，但拟合优度检验结果较为不理想；文献[6-10]为了准确认知系统可靠性，以对设备的结构和工作特性分析为基础，采用“浴盆曲线”模拟设备运行工况与退化过程；文献[11-13]基于故障类型和气候因素之间的关联关系分析，建立了不同气候条件下的设备故障率计算模型；文献[14-15]在不考虑经济性时，通过设备故障记录数据拟合其寿命模型曲线分析其可靠性.在设备故障率模型的求解方面，文献[16-22]运用残差检验数据拟合、极大似然参数估计等方法求得设备故障率的威布尔模型参数，并采用K-S检验法进行验证；文献[23]提出一种基于环境应力的设备可靠性评估方法，在不同的环境条件下，拟合设备的故障率曲线.但该方法多用于设备研发设计阶段，并不能完全适用于设备故障率的实际运行情况.

上述研究均考虑了设备故障率随其服役时间等不确定性因素变化的动态特性，为更符合设备实际运行情况，综合考虑牵引供电设备故障率模型的精确性与实用性，本文作者基于牵引供电设备运行故障记录及统计信息，考虑设备故障率函数的时变特性，建立牵引供电设备故障率的两参数威布尔模型并进行参数估计，拟合牵引供电设备的时变故障率函数曲线，基于K-S检验法对模型进行拟合优度检验.牵引供电设备故障率为开展地铁交流牵引变电所可靠性评估提供了数据支撑和条件保证，在实际应用中具有更好的准确性和适用性.

1 设备故障率时变特性分析

地铁交流牵引供电系统包括变压器、断路器、隔离开关、电缆、负序补偿装置和母线等关键设备.对于大多供配电设备而言，在其投运初期，由于内部构造还未磨合，必会造成设备失效频发，随着服役时间的推移，设备的故障率会随之降低.在其偶发故障期，设备故障率很低且在一定范围内保持基本恒定.在老化运行期，由于服役时间过久造成设备机械结构严重老化，会导致设备故障率迅速上升.由此可见，牵引供电设备故障率通常会随服役时间增加而变化，这种变化趋势可以被分为：初始运行期、稳定运行期和老化运行期等三个阶段[24].

在工程应用中，用于描述设备故障率随时间变化情况最常用的分布类型有指数分布、正态分布、对数正态分布和威布尔分布四种[24].威布尔分布具有描述多样性，威布尔分布的形状参数β决定了威布尔分布曲线的基本形状，通过改变β即可描述不同阶段下曲线的非线性变化趋势[25].当0<β<1时，曲线呈递减趋势；β≈1时，曲线基本为一条水平直线；β>1时，曲线呈递增趋势.而且通过改变β的值，威布尔分布也可以作为指数、正态和对数正态等分布的近似.威布尔模型可以较为全面、准确地描述牵引供电设备故障率随服役时间的变化规律，故选用威布尔分布模型作为设备的故障率分布函数.0<β<1、β≈1和β>1的情况分别适用于设备初始运行期、稳定运行期与老化运行期的故障率λ的建模分析[26]，牵引供电设备故障率λ与形状参数β之间的关系如图1所示.

2 设备时变故障率模型

基于牵引供电设备运行故障记录及统计信息，在设备故障数据的获取和预处理阶段，对同类设备按其时间顺序编号得到故障样本数据，其中样本量的大小决定了参数估计的准确性.威布尔模型参数估计阶段，参数未知的威布尔分布模型经线性化处理后可转换为线性回归方程.基于故障样本数据和中位秩估计，采用最小二乘法估计出牵引供电设备的故障分布参数后，再进行威布尔分布拟合优度检验，衡量设备实际故障分布与所求威布尔分布二者间的贴合程度，确定所求模型是否符合设备的实际运行情况，求得设备时变故障率函数曲线，进而对牵引供电设备故障率时变特性进行分析研究.牵引供电设备故障率时变特性分析流程图流程如图2所示，图2中Dm为检验统计量的观察值，Dm，a为K-S检验法的临界值，m为故障样本总数，a为显著性水平，通常a选择0.05[22]，即当故障样本数据服从威布尔分布时，其置信度为95%.

2.1 故障数据选取与预处理

牵引供电设备故障样本数据要根据相同投运时间、运行工况、厂家和型号等来筛选.每类设备的故障样本数据越多，求得的设备故障率时变参数越精确，设备故障率时变分布曲线越符合实际运行情况.同类型设备在相同运行工况下同时投运，统计记录每个设备发生故障时所经历的投运时长，把统计得到的投运时长按照从短到长的顺序排序，编号为p(p=1，2，…，m)，tp表示编号为p的牵引供电设备发生故障时所经历的投运时长.

2.2 威布尔模型参数估计

威布尔分布主要分为两参数威布尔和三参数威布尔分布，由于三参数威布尔表达式复杂，参数估计较困难，并且在实际工程中应用较少[25]，故采用两参数威布尔分布.牵引供电设备两参数威布尔分布的不可靠度F(t)为

(1)

式中：t表示设备的运行时间，η是尺度参数，记作t～(η，β).

牵引供电设备失效概率密度函数为不可靠度函数的导数，表示牵引供电设备不可靠度的变化速率，设备失效概率密度函数f(t)为

(2)

相应的，可靠度函数R(t)为

(3)

故障率函数λ(t)为

(4)

供配电设备寿命一般为10～30年[3]，可以根据设备故障样本数据对威布尔参数进行拟合估计.由威布尔分布表达式可知，一旦求得形状参数β和尺度参数η，威布尔分布即可确定.

在小样本情况下，牵引供电设备在投运时长tp时的不可靠度F(tp)可以按中位秩公式[27]近似处理为

(5)

式中：Fm(tp)为牵引供电设备在tp时中位秩经验分布函数；F(tp)为牵引供电设备在tp时的不可靠度.由于威布尔分布表达式为非线性，故需对不可靠度函数即式(1)两边连续作两次对数变换，将表达式转化为线性方程以便运用最小二乘法进行参数拟合.综上所述，得到两参数威布尔函数的线性回归方程为

y=Ax+B

(6)

其中，

(7)

A与B为回归方程系数，基于最小二乘法，A与B的估计计算式为

(8)

(9)

求得回归方程系数估计值A与B后，可根据式(7)计算设备的故障率威布尔估计参数β和η为

(10)

2.3 威布尔分布拟合优度检验

威布尔分布拟合优度检验是用于衡量设备实际故障分布与所求威布尔分布二者间的符合程度，基于K-S检验法[22]来验证假设建模的合理性与准确性,K-S检验中不同置信度水平下的Dm，a如表1所示.对于故障样本数据，每个数据对应的不可靠度F(tp)与中位秩经验分布函数Fm(tp)差值的最大绝对值即为检验统计量的观察值Dm，当Dm小于K-S检验临界值Dm，a时，认为牵引供电设备的故障样本数据服从假设的威布尔分布，则检验合格.其中

表1 K-S检验中不同置信度水平下的Dm，a

(11)

牵引供电设备故障率拟合优度检验通过后，便可求得牵引供电设备时变故障率曲线，设备每个时刻下的故障率具体数值都可以通过该曲线求得，从而能够更直观地获取牵引供电设备的故障率.基于牵引供电设备的实际运营数据进行参数估计，随着牵引供电设备投运时间的增长，牵引供电设备实际运营数据不断更新，故障样本不断增加，牵引供电设备的故障率威布尔函数也随之不断修正，因此分析牵引供电设备故障率的时变特性也更加符合实际运行情况，为牵引供电设备故障率的确定提供了参考，也为开展地铁交流牵引变电所可靠性评估提供了重要数据支撑和条件保证，降低了因故障率带来的可靠性评估误差，在实际应用中具有更好的准确性和适用性.

3 算例分析

以变压器为例，从文献[26]中的变压器故障记录表中选取故障数据，按投运时间由短到长的顺序排序编号，得到变压器故障样本数据如表2所示.

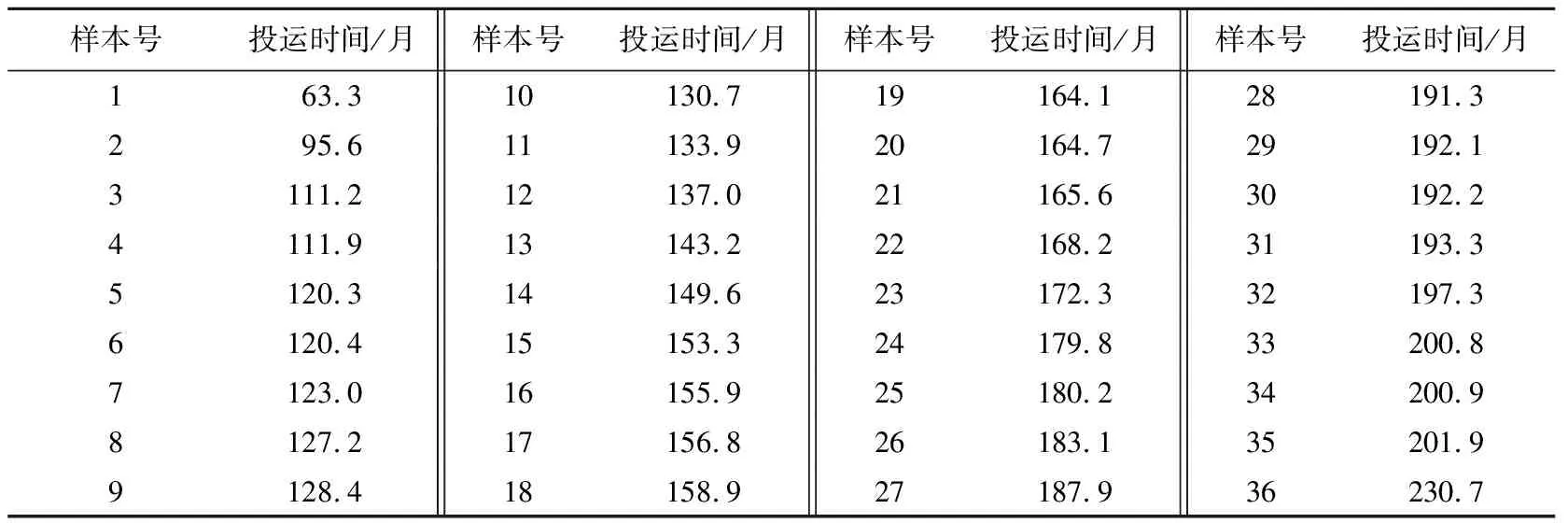
表2 变压器故障样本数据

当故障样本总数为36时，通过中位秩公式计算故障变压器的经验分布函数值，基于变压器的基础输入数据与牵引供电设备时变故障率模型分析步骤，利用最小二乘法计算各个数据量如表3所示.

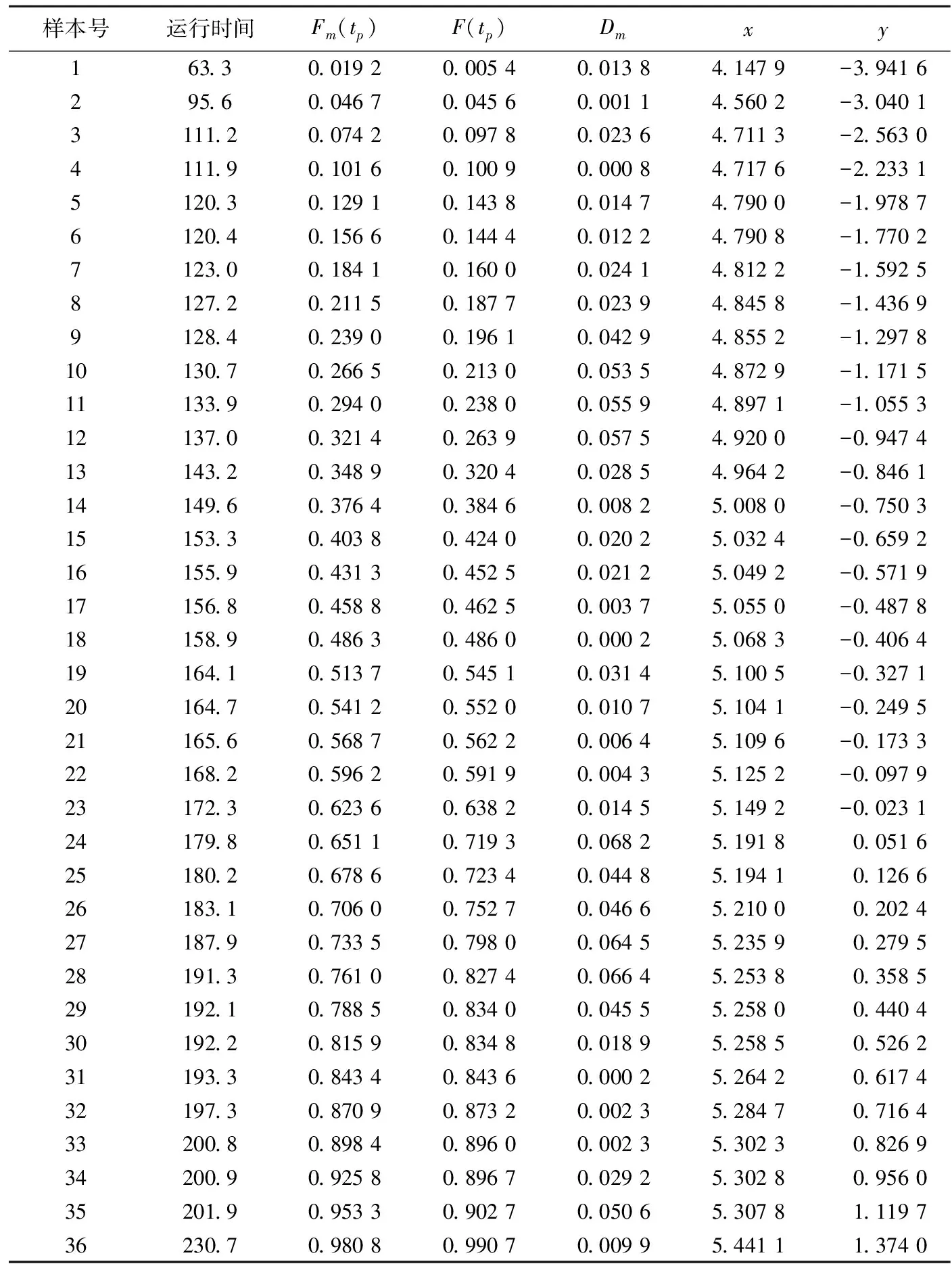
表3 最小二乘法中威布尔分布参数计算结果

基于表3中线性化处理后变压器故障样本数据(x，y)，利用最小二乘法拟合线性回归方程y=Ax+B，变压器故障数据的最小二乘拟合结果如图3所示.图3中直线为线性回归直线，散点为处理后的变压器原始故障样本数据.

基于线性回归方程系数A和B的估计值，进而求得变压器威布尔分布的形状参数β和尺度参数η的值为

(12)

当故障样本总数为36，置信度为95%时，临界值D36，0.05为0.227，观察值D36取Dm的最大值0.057 5，观察值D36小于临界值D36，0.05，验证了变压器故障样本数据服从参数为β、η的威布尔分布.变压器故障率模型参数确定后，变压器的不可靠度函数、可靠度函数、失效概率密度函数和故障率函数均可确定，分别为

(13)

(14)

(15)

(16)

分析变压器可靠性和故障率函数的时变趋势，可分别拟合出变压器可靠度函数、不可靠度函数、故障率函数和失效概率密度函数时变曲线图进行分析研究.变压器在投运使用前会经历一系列的试验，如冲击试验等，但由于缺乏投运前期变压器的试验数据，故本文只拟合出变压器在其偶发故障期和设备老化期内的故障率时变曲线，如图4所示.

由图4知，随着投运时间的增加，变压器可靠度曲线先是基本不变，而后逐渐降低，表示随着服役时间的增长，变压器可靠度逐渐下降.变压器故障率曲线由基本不变而后逐渐升高，表示变压器的故障率随服役时间经历了由基本不变到逐步累积的过程，且服役时间越长，变压器发生故障的可能性越大.变压器失效概率密度曲线由基本保持不变到逐步增加再到逐步下降，且在第165月左右达到最大值，表明变压器故障率函数变化率的变化趋势是由基本保持不变到逐步增加再到逐步下降，且在变压器运行至第165月时，变压器故障率的变化率达到最高，此时变压器故障率增长速度达到最快，变压器故障率递增趋势十分明显，变压器可靠度的降低速度也达到最快，故推断出变压器处于老化运行期.

5 结论

1)基于牵引供电设备的实际运营数据，采用两参数威布尔模型可求得牵引供电设备故障率时变参数，且随着服役时间的增加，故障样本不断更新，牵引供电设备故障率时变参数也不断随之修正.

2)以变压器为例，对其故障率时变特性进行分析研究.变压器运行至第165月时故障率增长速度达到最快，递增趋势十分明显，可靠度的降低速度也达到最快，推断出变压器处于老化运行期.

3)通过对牵引供电设备故障率模型的构建和参数求解，解决了以往研究中默认牵引供电设备故障率恒定不变的问题，为开展地铁交流牵引变电所的可靠性评估提供了数据支撑和条件保证，同时降低了地铁交流牵引供电设备故障率带来的可靠性分析误差，在实际应用中有更好的准确性和适用性.