高速铁路加筋土挡墙破裂面特征的模型试验及数值模拟

刘光鹏，肖 宏，杨松林，陆永港

(北京交通大学 土木建筑工程学院，北京 100044)

加筋土挡墙具有抗震性好、地基承载力要求低等优点，在铁路基础设施中得到广泛应用，国内外相关学者也进行了大量的理论及试验研究.文献[1]通过足尺模型试验与有限元软件模拟计算相结合，利用简谐荷载-模拟列车动荷载，计算分析了铁路加筋土挡墙动载下的力学特性.文献[2]利用数值模拟方法计算了加筋土挡墙在列车动荷载作用下不同筋材强度、不同速度作用下挡墙的变形.文献[3]通过3组模型试验研究了加筋土挡墙在施工填土过程中靠近挡墙面土的压实度对挡墙变形及筋体受力的影响.文献[4]利用室内模型试验与数值模拟相结合的方法，研究了加筋土挡墙在不同外荷载引起的沉降下，挡墙变形受土压力的影响情况.文献[5]通过大比例尺二级台阶式加筋土挡墙室内模型试验，监测了墙面水平位移、墙顶沉降及土工格栅的筋材变形，分析确定了铁路台阶式加筋土挡墙潜在破裂面的位置和形状.文献[6]进行了不同平台宽度的台阶式挡墙模型试验，分析了不同宽度对下部墙体的应力大小及分布规律的影响.文献[7]设计了大型现场激振试验，利用激振力来模拟高速铁路列车荷载，研究了加筋土挡墙在激振动荷载作用下挡墙内加速度、动土压力等的动态响应分布规律.文献[8]通过大型模型试验，加载了不同频率组合的简谐荷载，研究了加筋土挡墙在静动荷载作用下挡墙变形及土压力的分布规律.

由上述可以看出，目前大部分学者在研究动荷载时主要用简谐荷载来代替列车动荷载，这与实际列车作用不同，尤其是高速铁路，加筋土挡墙在列车高频作用下其力学特性表现及分布尚未得到系统研究，且目前铁路设计规范中也没有明确针对高速铁路加筋土挡墙在动载方面的受力及破裂面特征的详细计算规定.为了深入研究高速铁路加筋土挡墙在静动荷载作用下的变形及破裂面变化情况，本文作者开展了加筋土挡墙模型试验，建立了高速列车-轨道-加筋土挡墙路基耦合动力模型，计算分析高速列车行驶过程中挡墙变形及破裂面的变化，为其合理设计提供理论指导.

1 试验方案

1.1 试验概况

加筋土挡墙结构由挡墙面板和筋材组成，通过墙面板上的拉筋连接件将土压力传给拉筋，筋材与土体的共同作用，为路基基础提供支撑与抗变形能力.

以青荣城际DK315+913处的加筋土挡墙为背景.该处挡墙高为7.8 m，墙面板为C30混凝土预制而成，尺寸为0.5 m×0.3 m×0.3 m，面板模块内预埋格栅均采用EG260R高密度聚乙烯单向拉伸土工格栅，土工格栅的抗拉强度为260 kN/m，筋材长度为8.0～10.5 m，路基填土类型为中粗颗粒为主的砂类土A、B填料，现场压实度不小于0.92[9].

1.2 模型相似关系

由相似π定理可知，模型与原型的几何相似是现象相似的先决条件[10-11]，因此论文在加筋土挡墙模型设计时首先要确定它们之间的几何形似关系[12]，为了使试验结果更加贴近实际，充分考虑试验的操作性及可靠性，确定本试验的几何相似常数Cl=10，土体密度相似比Cρ=1，土体弹性模量相似常数CE=1，筋材材料的拉伸模量相似常数CEl=10，黏聚力相似比Cc=1，摩擦角相似比Cφ=1，泊松比相似常数Cμ=1.

1.3 相似材料的选取

考虑到砂土的性质相对明确，本模型试验采用中粗颗粒为主的砂土作为填料，通过筛分比试验确定，其粒径主要集中在0.23～2.36 mm，不均匀系数为2.67，砂土的最佳含水率为11%，压实度大于0.93，干密度为1.84 g/cm3，则达到最佳含水率时，砂土的密度ρ=1.84×(1+11%)=2.04 g/cm3.

墙面采用模块式墙板，考虑到模型试验实施的方便，经过对比分析计算得出：通过对实木板进行增厚3.3倍，即可确保木板块具有足够的强度来保证其材料本身的抗变形能力.通过相似理论计算得木板的尺寸为5 cm×3 cm×10 cm，木板的长宽与实际相似，厚度在相似尺寸的基础上增大3.3倍.筋材与面板墙参照现场实际挡墙特点，采用机械连接方式，通过对木板进行竖向钻孔，然后采用钢钎将木板拼接成整体.由于实际现场的筋材抗拉强度为260 kN/m，因此本模型试验采用单向拉伸的土工格栅作为加筋材料，其标称抗拉强度≥26 kN/m，其他相应的物理力学特性为：标称抗拉强度≥26 kN/m；屈服伸长率≤10%；2%伸长率时的拉伸力≥7 kN/m；5%伸长率时拉伸力≥14 kN/m；单根筋材间隔30 mm；单根筋材厚度1 mm.

1.4 模型箱与试验方案设计

模型箱的三个面为1.5 cm厚的钢化玻璃.现场实际挡墙底端为混凝土条形基础，为了模拟现场实际条形基础对挡墙底端变形的限值作用，在挡墙底端焊接横向槽钢横挡，模拟现场实际的挡墙底端限制条件.

模型箱尺寸由几何相似关系确定，长×宽×高为1.2 m×0.6 m×0.8 m，箱内填土高度为0.78 m，采用分层填筑，锤击法压实，试验压实度在土工实验室内进行测试控制，最终控制填土压实度不小于0.93，略大于实际现场的填土压实度0.92.

挡墙顶端中间位置设置加载板，采用压力传感器控制千斤顶进行精确加载.根据铁路设计规范[13]，有砟轨道路基面最大设计静荷载为54.1 kPa，因此最大加载为54.1 kPa.同时为了研究顶部荷载在线性增大关系下挡墙的变形规律，进行了逐级加载，分别为：10、20、30、40、50、54.1 kPa.

采用电阻式微型土压力盒测试土压力，土压力盒的量程为10 kPa.挡墙内部水平土压力盒的埋设采用反开挖方式进行，即填料高度超过土压力盒设计高度位置后反开挖，将压力盒放入并回填压实.在填筑到图1(a)垂向土压力盒安装的位置时，采用高强度AB胶将垂向土压力盒固定在木板上，填土时先填筑远离面板区域的土体，再填筑压实面板附近的土体，通过以上措施达到对土压力盒位置的准确控制.利用电子百分表对挡墙变形进行监测，利用数据采集仪对土压力进行采集与监控，具体试验仪器布置如图1(a)所示，其中HD为横向位移计，VD为垂向位移计；现场试验如图1(b)所示.

由于筋材间距和长度是加筋土挡墙设计的主要因素，结合实际情况与试验操作条件，进行了3组不同筋材间距及长度的试验，3组工况如表1所示.

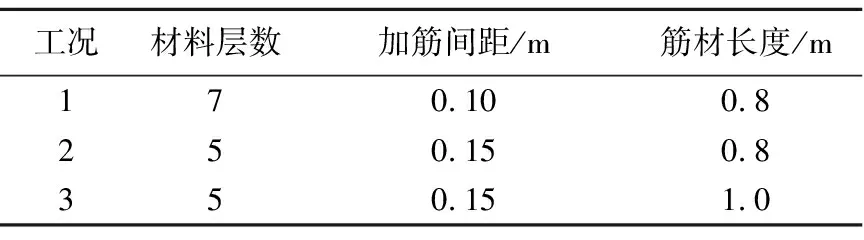
表1 试验工况列表

2 试验结果与分析

2.1 挡墙垂向变形

在静荷载作用下，分别对不同工况的挡墙垂向位移进行了测试，具体测点位置见图1(a).最终挡墙垂向位移为图1(a)中两侧加载板VD-1和VD-2距离的一半.不同工况下的挡墙垂向位移变化情况如图2所示.

由图2可知，工况1的位移最小，工况3的次之，工况2的位移最大.说明总体上加筋层数多的挡墙垂向位移相对较小，加筋层数对挡墙的变形控制效果最为明显.

对比工况1、2可知，整体上工况1的墙顶垂向位移小于工况2的位移，即筋材层数越多挡墙顶面的垂向位移越小.加筋层数由5层增加到7层，在最大荷载作用下挡墙顶端垂向位移减小了7%.

对比工况2、3可知，整体上工况3的墙顶垂向位移小于工况2的位移，即筋材越长挡墙顶面的垂向位移越小.筋材长度由0.8 m增大到1 m，挡墙顶端位移减小了3%.

2.2 挡墙横向变形

每个工况有6组数据，具体测点位置见图1(a).由于每个加载力的变化规律基本相似，取最小、中间及最大加载的3组挡墙横向位移数据进行对比分析，不同筋材间距及长度对比数据见图3.

从图3可以看出，不同静载作用下总体上挡墙横向位移均为先增大后减小，墙面横向变形最大值均出现在挡墙0.5H附近.

由图3(a)可知，整体上工况1产生的挡墙横向位移比工况2产生的位移要小，即加筋层数越多，挡墙的横向变形越小.加筋层数由5层增加到7层，挡墙横向方向最大变形减小了8.5%.因此增加筋材层数可以增大加筋土挡墙的横向抗变形能力.

由图3(b)可知，整体上工况3产生的挡墙横向位移比工况2产生的位移要小，即筋材越长，挡墙的横向变形越小.筋材长度由0.8 m增大到1 m，挡墙横向方向最大变形减小了5%.可见增大加筋材料的铺设长度可以增大加筋土挡墙的横向抗变形能力.

2.3 挡墙内土压力

在静荷载作用下，分别对加筋土挡墙面不同高度侧向土压力进行了测试，得出不同加筋铺设层数挡墙面侧向土压力对比情况如图4(a)所示，不同筋材长度土压力对比情况如图4(b)所示.

从图4可知，墙背水平土压力沿着墙高从上往下逐渐增大，且呈非线性分布.随着外荷载的逐渐增大，不同墙高处的墙背水平土压力变化幅度不同，其中靠近挡墙底部的水平土压力变化比较明显，越往上变化幅度越小，这主要是因为墙面的变形会释放墙背处的部分水平土压力，且越靠近挡墙上部，受到墙面变形的影响也就越大.

对比图4(a)中工况1、2中的数据可知，总体上在挡墙的底端工况2的土压力要比工况1的土压力大，说明加筋层7层的要比加筋层5层的挡墙底端受到的土压力小.

对比图4(b)中工况2、3中的数据可得，总体上工况2的土压力要比工况3的土压力大，说明筋材长的要比筋材短的挡墙底端受到的土压力小.

3 有限元分析

3.1 模型建立

通过静力模型与试验结果对比，验证材料参数及接触关系本构的正确性，进一步通过动力模型计算高速列车行驶过程中挡墙变形及破裂面的变化规律.

静动力模型中路基土体本构模型采用摩尔库伦材料本构，筋材与土体之间采用嵌入式接触关系.筋材采用梁单元模拟，通过给梁单元赋予筋材的截面属性，准确模拟筋材的物理性能.动力模型中的钢轨、轨枕及道床均采用弹性实体模拟.扣件采用弹簧-阻尼单元模拟，竖向刚度为100 MN/m，竖向阻尼为6×104N·s/m，扣件间距为0.6 m.

模型(长×宽×高)为12 m×6 m×7.8 m，模型中轨道结构、土体及筋材参数见表2，通过ABAQUS有限元软件建立的静力计算模型见图5.

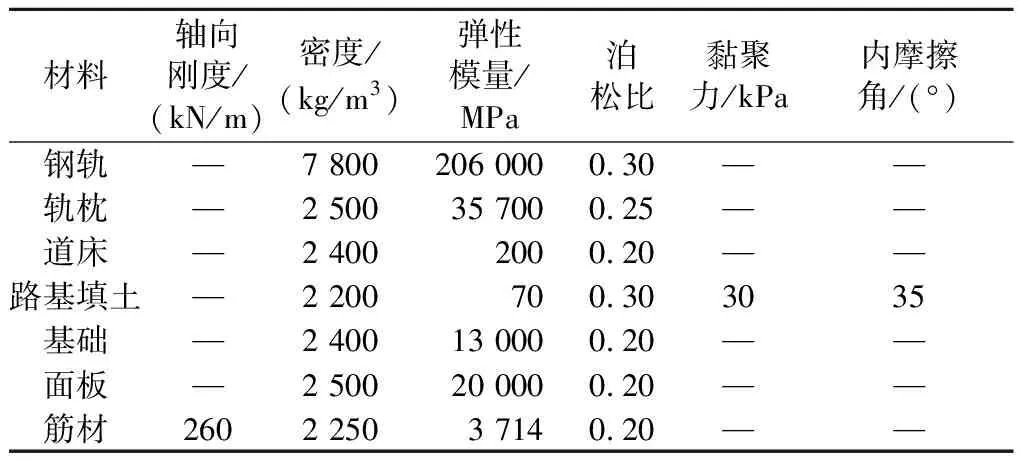
表2 土体及筋材材料参数表

静力荷载是通过在图5中的位置施加分布压力荷载从而实现静力荷载的逐级施加.

动力模型中车辆主要通过轮对-转向架-车体组成的多刚体系统模型来实现，通过对轮对-转向架-车体系统中施加速度边界荷载来实现车体沿轨道线路纵向移动的目的.动力模型中车辆的相关参数按照文献[14]的规定选用，其中车辆轨道之间采用非线性赫兹接触关系计算，即

P(t)=[ΔZ(t)/G]3/2

(1)

式中：P(t)为轮轨法向应力，N；ΔZ(t)为t时刻轮轨间的弹性压缩量，m；G为轮轨接触常数，对于锥形踏面车轮，G=4.57R-0.149×10-8(m/N2/3)，其中，R为车轮半径，m.

为了消除挡墙纵向长度的边界效应影响，将挡墙区域之外的钢轨和轨枕在其底面施加垂向位移限制边界条件，挡墙内的钢轨、轨枕与道床路基设置正常的接触关系，挡墙底端施加不动位移边界条件，挡墙的四周也分别施加相应方向的位移限制边界条件.建立的车辆-轨道-加筋土挡墙路基空间耦合系统各部件间的连接方式及传递关系如图6所示，具体对应的有限元模型见图7.

3.2 模型验证

静力计算模型中取与试验相同的荷载，分别为10、20、30、40、50、54.1 kPa，通过在模型顶面中间(图5位置)施加分布的压力荷载，计算出静力加载情况下挡墙垂向位移云图如图8所示，取模型试验相同位置的垂向位移与试验结果进行对比，如图9所示.

由图9可以得出，数值模拟结果和试验结果分布规律、走向及最终位移大小基本一致，验证了土体与筋材本构模型及材料参数选用的合理性.

3.3 列车行驶中挡墙变形及破裂面变化

当城际铁路列车以250 km/h的速度运行时，挡墙正中间位置横向位移随列车运行时间的变化如图10所示.

从图10可以看出，在0.9 s左右列车第一个转向架经过挡墙中间位置，在1.2 s左右列车第二个转向架经过挡墙中间位置.当列车转向架经过挡墙中间时，挡墙横向位移出现两个明显的峰值.与静位移相比，列车作用下的动位移具有明显的随时间动态变化的规律，同时当列车轮对经过挡墙时，挡墙位移达到最大.

分别计算了不同筋材间距及长度对应的加筋土挡墙横向变形，挡墙的横向位移最大值如图11、图12所示.

从图11中可得出，随着筋材间距的增大，挡墙的横向变形明显增大，筋材间距由0.5 m增大到0.8 m，挡墙横向位移增大了23.6%.

从图12中可得出，随着筋材长度的变短，挡墙的横向变形明显增大，筋材长度由9 m缩短为6 m，挡墙横向位移增大了19.8%.

可见筋材间距及筋材长度对加筋土挡墙的变形影响较大，同时在当高速列车驶过挡墙时，挡墙横向位移最大值均出现在挡墙底端向上约0.2H处.相比较静载作用，动载作用下挡墙的最大位移出现在挡墙底端0.2H处，因此建议在高速铁路加筋土挡墙设计中应加强挡墙底端0.2H位置的结构强度设计.

分别计算了高速列车经过不同筋材间距及长度加筋土挡墙最大主应变变化情况,具体如图13所示.

从图13(a)～ 图13(d)中可以看出，随着筋材间距的增大，筋材长度的变小，加筋土挡墙内应变集中红色区域的面积相应增大，路基发生滑动破裂的概率也相应增大.可见，通过减小筋材间距及增大筋材长度可以使动力作用下挡墙内土体产生的破裂带面积减小，进一步的起到对整个土体加强加固的作用，从而降低产生滑裂的概率.

为了分析动力作用下的破裂带位置与传统的朗肯破裂面及铁路规范破裂面在空间上的位置关系，将其做于同一图中，如图14所示.

从图14可知，朗肯破裂面计算的破裂面相对偏小，不能完全包住滑裂带范围.我国铁路设计规范[15]中通过(0.3H，0.5H)计算得出的破裂面相对较保守，其斜线部分基本可以包住滑裂带.因此在高速铁路加筋土挡墙破裂面计算当中，应综合考虑动载作用影响.

对不同筋材间距及筋材长度的模型进行计算，通过将其主要的滑裂区域进行研究分析，得出其最主要的滑裂区域在图15中两条白线之间，其中上面线的起点约在挡墙的0.154H位置处，下面线起点在挡墙底端，分别求出不同工况下两条白线与挡墙间的夹角θ1和θ2，如表3所示.

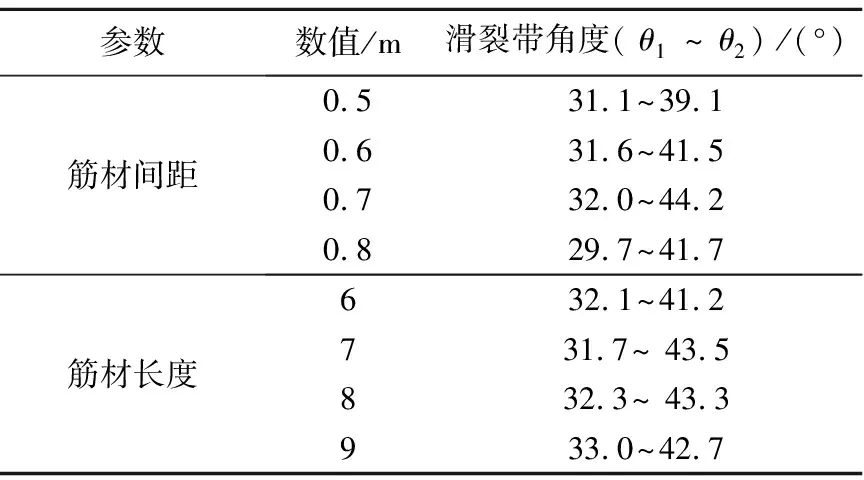
表3 不同筋材间距及长度对应的滑裂带角度

从图15及表3中可以看出，不同筋材间距及筋材长度对应滑裂带所在区域均出现在30°至45°之间，基本在45°-3φ/7～45°区域内，φ是土体的内摩擦角.

滑裂带断面中每层筋材应力分布情况见图16.

从图16中可以清晰看到每层筋材应力分布情况：最大值所在位置、破裂面的大致趋势及形状.图16中红色圈范围内筋材应力明显较大，即筋材最有可能断裂是从第3层筋材开始向上发展.

将不同筋材长度对应破裂面内筋材最大应力位置找出，并将其位置坐标连成线，得出如图17所示的破裂面.

由图17可知，不同筋材长度对应的破裂面位置基本没有发生大的变化，通过对其线型进行拟合得出，高速铁路列车运行过程中，挡墙内产生的破裂面为从挡墙底端向上约0.15H处的一条曲线，大概呈指数型分布.

将文本中动力计算得出的破裂面与其他文章或规范中的破裂面进行比较，如图18所示.

由图18可知，与传统的朗肯破裂面及0.3H裂面相比，本文计算得出的破裂面为经过底端向上0.15H处的一条指数型曲线，能够更好地反映列车动荷载作用下加筋土挡墙的破裂情况.同时与相关文献[16]中实测的破裂面相对比，其基本走向、大小规律与本文计算的基本一致，证明本文计算结果的正确性.本文计算的破裂面对于以后的高铁加筋土类似挡墙破裂面计算具有一定的指导意义.

4 结论

针对静载及列车动载下加筋土挡墙变形及破裂面变化情况进行了3组模型试验，建立了高速列车-轨道-加筋土挡墙三维耦合模型，计算分析了相关问题，并与规范值进行了比较，得出如下结论：

1)静载作用下挡墙最大变形出现在挡墙中部附近，而高速列车动载作用下挡墙最大变形出现在底端附近，因此建议在以后高速铁路加筋土挡墙设计中应对挡墙底端附近区域进行动态设计检算.

2)加筋土挡墙在高速列车动载作用下，会出现应变集中的滑裂带，与朗肯破裂面相比后者数值较小，与铁路规范中破裂面相比后者相对保守，因此在高速铁路加筋土挡墙破裂面计算中应考虑采用列车动载进行设计计算.

3)动载作用下的滑裂带基本由经过底端及底端向上0.154H处的两条直线组成的区域内，这两条直线与挡墙的夹角在45°-3φ/7～45°范围之间.

4)动载作用下的破裂面是经过挡墙底端向上0.15H处的一条指数型曲线，而传统铁路规范计算的破裂面为经过挡墙底端的一条直线，该计算结果可为今后高速铁路加筋土挡墙破裂面的准确计算提供一定的参考.