基于TMD的U型梁结构低频振动控制研究

罗 锟，张新亚，王鹏生，雷晓燕

(华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013)

近些年，轨道交通凭借其运量大、快捷、安全的特点得以快速的发展.高架桥具有工后沉降低、节约土地、建设周期短等诸多优点，更是在轨道交通中取得了广泛的应用[1].其中U型梁与上承式的箱型、T型梁等相比，建筑高度低，并且腹板的设计使其具有更好的降噪效果[2]，在城市轨道交通中应用广泛.但是混凝土U梁的振动也会向周围环境辐射噪声，该噪声以0～200Hz的较低频段为主，对人的注意力、反应时间及语言辨识能力等有诸多负面影响[3-4].因此寻求有效的振动噪声控制技术，对于保护城市环境以及促进轨道交通的发展都具有重要意义.

振动控制方法包括不需要外部能量注入的被动方法和需要外部能量注入的主动方法[5].调谐质量阻尼器(Tuned Mass Damper ,TMD)作为一种有效的被动控制方法，由附加质量块、弹簧以及阻尼组成，在桥梁振动控制技术领域，已有学者展开相关研究.肖新标等[6]研究了TMD对移动荷载作用下桥梁振动的控制规律；Chen等[7]以Timoshenko梁为研究对象，研究了在移动作用力下附加TMD后的振动控制效果；王浩等[8]以南京长江大桥为研究对象，研究了TMD在该桥减振控制中的参数敏感性和控制效果.沈昭等[9]对某人行桥结构进行行人荷载下的结构动力特性分析, 对比了添加TMD前后结构的加速度响应, 表明TMD系统减振效果显著，TMD在其刚度和阻尼系数取值合理时可达到最优控制效果.但是TMD减振鲁棒性较差，减振效果易受主结构振动频率偏移的影响，为改善这一问题，Clark[10]首次提出多重调谐质量阻尼器(Multiple Tuned Mass Damper, MTMD)，使得TMD的控制效果更加稳定；张迅等[11]选取32 m双线混凝土简支箱梁为研究对象，建立了移动集中力-桥梁-MTMDs耦合振动模型，发现MTMDs对于控制桥梁的振动响应幅值有很好的效果，但是仅对一阶固有竖向弯曲频率处的结构振动减振效果明显，对拓展减振频率范围效果不佳.

通过总结现有研究结论发现，针对桥梁结构振动特定频率附近的减振，传统TMD、MTMD具有明显效果，但是减振频率范围较小.基于现阶段研究局限性，本文作者旨在提升TMD控制桥梁振动的性能，以高架U梁结构为研究对象，识别多自由度桥梁系统的等价质量，并基于TMD定点理论，进行控制多阶模态振动的TMD设计，仿真研究安装TMD后的减振效果，为高架轨道桥梁结构的减振降噪设计提供参考.

1 TMD设计方法

1.1 TMD最优设计参数

当U型梁结构附加了TMD之后，振动能量通过TMD系统的阻尼元件得以消耗.高架U型梁结构作为一个连续体系统，在进行附加TMD设计时，不能够直接采用单自由度系统TMD的设计理论[12]，然而U型梁可以离散成为一个多自由度系统，如图1(a)所示，而进行工程仿真计算时，多自由度系统可以看做为多个单自由度系统的集合，如图1(b)所示，然后进行每个单自由度系统参数的设计[13].

利用模态分析技术将U型梁结构离散为多个单自由度集成的非耦合多自由度模型，并基于模态向量的正交性，求得对应第i阶模态的等价质量为

Mi=2Ttotal/(ωixj)2=

(1)

式中：Mi为具有物理意义的第i阶模态的等价质量；Ttotal为U型梁系统的单元总动能，通过有限元模态分析获得；ωi为第i阶模态固有原频率；(m1,m2，…，mj，…，mN)为各单自由度集合的质量；(x1,x2,…,xj,…,xN)为U型梁结构第i阶模态的振型向量.

在理论上，当忽略主系统的阻尼时(通常混凝土阻尼很小)，单自由度TMD设计存在着最佳的配置参数，在计算得到第i阶模态的等价质量之后，可计算U型梁第i阶模态附加TMD的最优参数分别为

αopt=1/(1+μi)

(2)

(3)

Ci=4παoptβoptfimi

(4)

(5)

式中：μi为U型梁第i阶TMD质量mi与模态等价质量Mi的比值；αopt为TMD系统与主结构系统的最优频率比；βopt为TMD系统与主结构系统的最优阻尼比；fi为主结构受控模态的频率，Hz；Ci、Ki分别为第i阶模态附加TMD的设计阻尼系数和刚度系数.

由此可知，在进行TMD设计时，获取受控模态等价质量和模态频率，并拟定质量比，即可求得受控模态TMD的最优配置参数.

1.2 TMD最优安装位置

根据文献[14]，TMD控制主结构振动的效果，与其选用的质量比大小相关，质量比越大，减振效果越好.而在确定了TMD系统质量之后，安装位置便进一步影响着减振效果.

由式(1)可得，当xj最大时，即质点j点位于被控结构第i阶模态的波腹位置，求得模态的等价质量最小，则在确定了TMD质量的情况下，相对质量比为最大；当xj最小时，即质点j点位于被控结构第i阶模态变形最小的位置，求得等价质量为无穷大，在减振TMD质量一定的情况下，质量比约为零.所以为了得到最好减振效果，TMD的安装位置应选择被控模态的波腹位置处.而且位置尽可能选择在其他模态的节点位置，以减少模态间的相互干扰.

2 U型梁受控模态分析

上海某轨道交通线高架段为双线分离式简支U型梁，长30 m，桥梁结构弹性模量为34.5 GPa，密度为2 500 kg/m3，泊松比为0.2，支座刚度3.38×106kN/m，进一步建立U型梁有限元模型如图2所示.

U型梁混凝土结构采用solid45单元模拟，为仿真桥梁实际的边界条件，选用弹簧-阻尼单元Combine14模拟桥梁4个弹性支座，结合工程实际确定参数值：垂向刚度Kq=3.38×106kN/mm，阻尼为Cq=105N·s/m.采用映射网格划分法对U型梁结构进行划分，最小单元尺寸0.1 m.附加TMD系统的质量块和刚度阻尼元件分别采用质量单元Mass21和弹簧-阻尼单元Combine14进行模拟，以振型贡献率[15]为评价依据确定U型梁受控模态.U型梁前15阶模态固有频率及振型贡献率如表1所示.本文关注U型梁竖向的振动响应，故研究U型梁结构的Y向振动模态.由表1振型贡献率的分布可知，U型梁以1阶竖向振动为主，其次第6、9和11阶模态贡献也相对较大，故选择1、6、9和11阶模态为受控模态，其振型如图3所示.

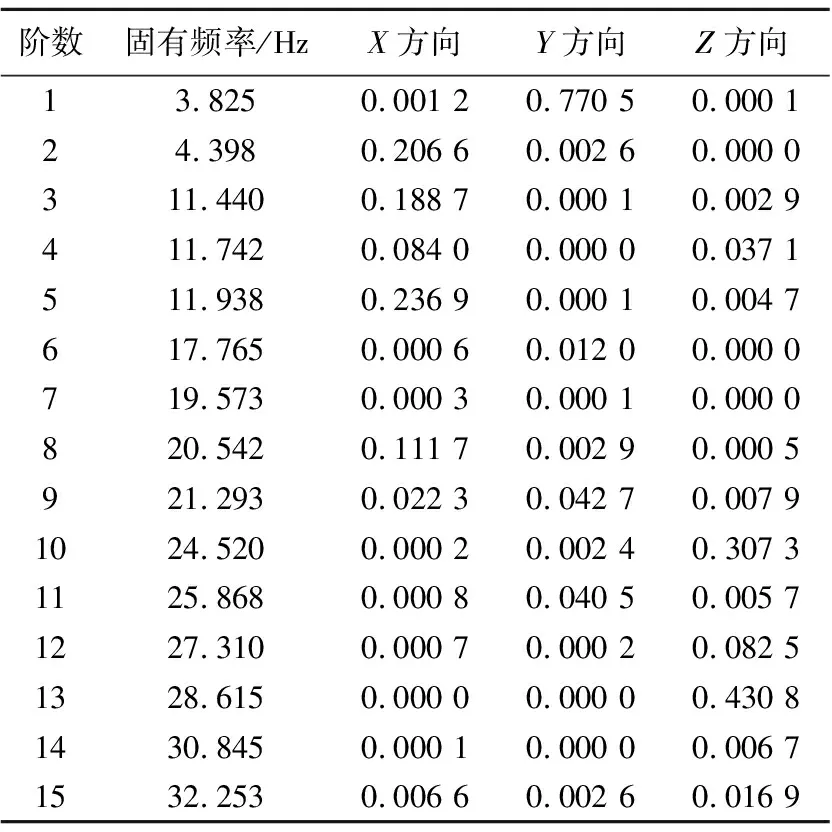
表1 U型梁自振频率及振型贡献率

3 TMD减振特性分析

3.1 单位简谐荷载作用下TMD减振特性

为了探讨在简谐荷载作用下，附加TMD的振动控制效果，在U型梁结构上施加单位简谐荷载，荷载位置应能够明显激起该阶模态的竖向共振.进行谐响应分析得到U型梁单独附加控制各阶模态的TMD时，振动监测点处的加速度幅频响应.

以第1阶模态振动控制为例，基于各阶模态等价质量的确定方法，通过模态分析获取U型梁结构第1阶模态单元总能量、模态位移的最大值和固有频率，控制频率为3.825 Hz，根据式(1)计算得到第1阶模态的等价质量，TMD质量比μ分别取0.01、0.02、0.03和0.04，得到控制1阶模态振动的TMD最优参数设计表2所示.

表2 TMD最优设计参数

图4给出了U型梁第1阶模态附加TMD选取不同的质量比时，U型梁跨中振动监测点的幅频响应，计算中单位简谐荷载施加在跨中截面对应钢轨线位置处.

由图4可知，附加TMD之前，U型梁1阶固有频率附近的竖向振动位移响应出现较大的幅值，而在附加了TMD后，响应峰值出现明显的降低，体现了TMD中弹簧阻尼单元对1阶固有频率附近振动能量的消耗.随着质量比的增加控制效果愈加明显，但是减幅呈减小趋势，所以从经济性和结构强度的角度考虑，质量比的选取也不宜过大.

3.2 移动荷载作用下TMD减振特性

3.2.1 多阶模态TMD最优参数设计

基于高架U型梁结构附加TMD减振系统最优参数设计理论，对U型梁结构同时附加四阶模态TMD开展减振特性分析.基于减振设计的经济性和结构强度的稳定性，并考虑到第1阶模态频率振型贡献率较大，μ取0.03，第6、9和11阶模态TMD的μ均取为0.02，得到最优设计参数如表3所示.

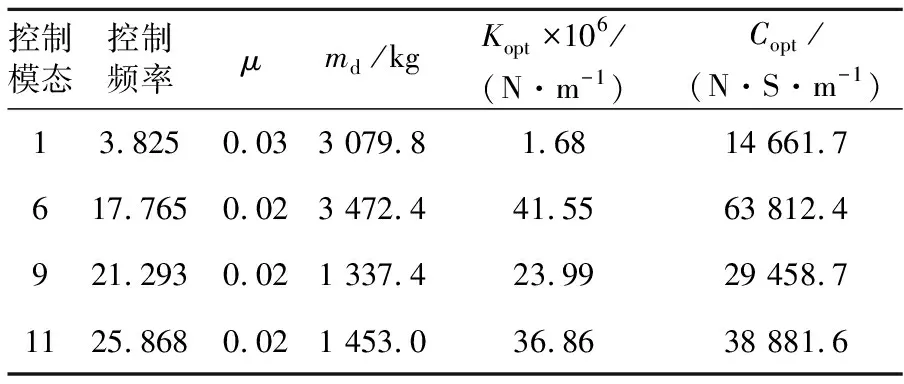
表3 多阶TMD最优设计参数

3.2.2 TMD最优附加位置选择与测点布置

控制各阶模态振动的TMD在高架U型梁结构底板的安装位置如图5所示.由图3(a)U型梁第1阶模态振型图可见，该阶模态的波腹位置位于跨中截面边缘位置，所以可将控制U型梁1阶模态振动的TMD安装在A点；由图3(b)U型梁第6阶模态振型图可见，该阶模态变形最大位置位于距离梁左端4.32 m位置，所以选择B点作为第6阶模态TMD的最优附加位置；由图3(d)U型梁第11阶模态振型图可见，该阶模态变形最大位置位于跨中截面D点，所以选择将D点设为第11阶模态TMD的最优附加位置；由图3(c)U型梁第9阶模态振型图可见，该阶模态变形最大位置位于跨中截面和距离梁右端4.48 m截面的位置，由于第1阶和第11阶的波腹也位于桥梁的跨中，为了减少多阶模态TMD间模态耦合作用下的相互影响，考虑将控制U型梁第9阶模态振动的TMD安装在C点.

U型梁各阶模态的波腹与节点位置沿桥梁纵向的分布存在差异，因此TMD控制各个截面振动的效果也不同.为了研究附加TMD前后不同截面位置的减振效果，选取跨中、四分之一以及支座截面作为观测截面，如图6(a)所示，并分别在各截面底板处选取1个振动监测点.以跨中截面为例，测点布置如图6(b)所示.

3.2.3 减振效果评价

讨论TMD的减振效果，为了简化计算，仅考虑一节地铁列车匀速通过该高架U型梁，运行速度V=40 km/h，并将列车荷载简化为作用在U型梁钢轨线位置上的移动集中力(4×65 kN),荷载模型如示意图7所示.编写加载程序，并采用有限元分析软件Ansys进行瞬态分析，积分时间步长0.011 25 s，分别在时域和频域范围内对比分析减振前后U型梁的振动特性.

计算U型梁结构同时附加四阶模态TMD前后振动监测点的时域和频域的响应.图8～图10分别给出了U型梁支座、四分之一和跨中截面监测点的竖向振动加速度时程和幅频曲线来分析减振效果.

观察图8(a)、9(a)和10(a)减振前后U型梁竖向振动加速度时域曲线对比，可以明显看出一节地铁列车通过的痕迹，并且减振后支座截面、四分之一截面和跨中截面的最大加速度响应幅值分别降低19.2%、28.1%、45.3%，并且附加TMD后，U型梁整体阻尼增加，使得列车过桥加速度响应衰减加快.同时，计算附加TMD减振前后各截面振动监测点的Z振级如表4所示，由表4可知，附加TMD后，对跨中截面的振动控制效果最佳.

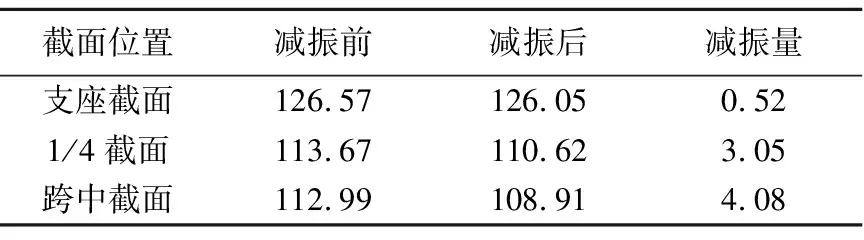
表4 减振前后Z振级

观察支座截面底板加速度幅频曲线图8(b)可知，附加TMD之后，移动荷载引起的U型梁结构振动加速度在固有频率21.293 Hz、25.868Hz附近出现的峰值响应显著降低；由四分之一截面底板幅频曲线图9(b)可知，U型梁振动加速度除了在固有频率3.461、17.765、21.293和25.868 Hz附近均出现较大的峰值外，还在10 Hz附近激起了新的共振峰值，而附加TMD后，控制频率附近的振动加速度响应明显降低；由跨中截面底板幅频曲线图10(b)可知，未附加TMD时，移动荷载引起的U型梁振动加速度在固有频率3.461、17.765、21.293和25.868 Hz附近均出现较大的峰值，而附加TMD后，荷载引起的U型梁振动加速度在固有频率附近频段3.461、15～28 Hz的振动加速度显著降低，从而表明TMD有效控制了U型梁结构前几阶模态的竖向低频(0～31.5 Hz)振动.

计算附加多阶TMD前后，U型梁支座截面、四分之一截面和跨中截面振动加速度级的1/3倍频程曲线如图11所示.由图可知：支座截面16～31.5 Hz频段的振动加速度级相差明显，振动加速度级可降低2～6 dB；四分之一截面在2.5～5、12.5～31.5 Hz频段的振动加速级均明显降低，最大分别降低2、4.2 dB；跨中截面振动加速度级也在2.5～5、12.5～31.5 Hz频段发生明显衰减，最大可降低4.7 dB.从而验证了采用多阶TMD控制U型梁低频振动的有效性.

4 结论

1)U型梁以1阶竖向振动为主，第6、9和11阶模态贡献也相对较大，可同时作为受控模态进行附加TMD的设计.

2)基于多自由度系统等价质量识别法和TMD定点理论，可以实现对高架U型梁结构附加TMD系统的最优化设计.

3)TMD减振系统能够有效控制U型梁结构的低频共振，并且质量比越大，对U型梁结构振动控制效果越明显，但是随着质量比的增大减幅逐渐变小.

4)移动荷载作用下，附加一定质量比组合的多阶模态振动TMD减振系统后，U型梁结构低频振动控制明显，在固有频率附近频段3.461、15～28 Hz的振动加速度水平显著降低.