客货混行条件下列车运行调整模型及算法

查伟雄，张子悦，严利鑫

(华东交通大学 交通运输与物流学院，南昌 330013)

铁路行车调度指挥工作是列车正点运行的重要保障，编制列车运行计划、保证列车正点运行是调度指挥工作的核心.列车在运行过程中受各种随机扰动的影响，容易偏离图定运行时间，影响行车效率.如何在短时间内进行高效、有序的列车运行调整，保证行车安全，是衡量区段内行车组织工作质量的标准，也是近期的热点和难点问题.“最优列车调度”问题由Szpigel[1]首次提出，以列车开行时间最小为目标建立线性规划模型.既有文献对旅客列车运行调整问题展开研究，通过建立混合整数规划模型，分别采用两阶段法[2]、拉格朗日松弛算法和最短路径算法[3]、策略优化方法[4]及仿真[5-6]等优化方法，以列车偏离图定运行时间最短为目标进行求解.近年来，许多学者采用智能算法，如遗传算法[7]、粒子群算法[8]等来解决列车运行调整问题.文献[9]建立基于最小列车秩序熵的模型求解，实例证明了仅对受轻微扰动的单线客货混行条件下列车运行调整的问题有效.文献[10-11]针对客运铁路网络下的货物列车运行调整问题，以客、货列车延误时间最短、货物列车旅行时间最短为目标建立优化模型，采用启发式算法求解.文献[12]研究了基于超图的两级建模，考虑旅客时刻表延误和货运时间，利用问题特殊结构的修正线性化求解.上述文献基于双线铁路网络，对客货混行列车运行调整问题进行研究.

本文作者以客货混行条件下的单线铁路全线为背景，以列车间隔时间和到发线等为约束条件，建立列车运行调整计划混合整数规划模型.以列车在调度区间内总的偏离图定运行时间最少为目标函数，采用自适应柯西变异人工蜂群算法(ACMABC)求解，并通过实例验证了模型及算法的可行性.

1 问题描述

列车运行调整的目标是恢复正点运行，当列车在运行过程中偏离图定时间发生晚点时，调度指挥人员需遵守以下原则实施调整：①若为同等级列车发生晚点，则正点列车优先，晚点列车后行；②若为不同等级列车发生晚点，则部分高等级列车可接受低等级列车一定时间的连带晚点,其他列车绝对优先；③若在晚点传播情况下进行调整，则低等级列车不得越行高等级列车.

根据以上原则，基于客、货列车混行的特点，本文采取以下调整策略：①减少列车在车站作业时间.当部分列车在车站作业时间较长时，可以适当压缩列车在车站作业时间，但需满足车站的最小作业时间约束；②列车越行.当前行列车出现到达晚点并对后续列车产生晚点传播时，若满足两列车的最小间隔时间约束，且后续列车优先级高于前行列车时，可实现越行；③组织列车赶点.当列车发生晚点时，可在满足不同等级列车在区间的最小运行时间约束条件下，通过区间加速方式实现正点运行，提高行车效率；④运行调整时间的确定.当前行列车出现晚点并影响到后续列车时，运行调整时间为列车最小列车间隔时间、实际到达时间与图定到达时间差值的最小值.

由于列车运行调整问题涉及条件较多，故作以下问题假设：列车的图定到、发时间已知，列车在偏离图定运行前保持正点运行，列车在任一站点可越行.

2 模型的建立

2.1 符号定义

假设某一单线半自动闭塞区段有m次列车，n个站点，n-1个区间.令Qt为列车车次集合，其中包含各等级旅客列车Qk和货物列车Qh，Qt=Qk∪Qh={Qt1,…,Qtg,…,Qtm}，Qk={1,…,g}，Qh={g,…,m}；令Qs为车站站点集合，Qs={Qs1,Qs2,…,Qsn}；令K为区间集合，K={1,2,…,n-1}；令Dj为车站j的到发线集合(j∈Qs)，则列车运行调整中可用的资源集合为Φ={Qs,Qt,K,Dj}；令A0、D0分别为图定列车到、发时刻，A、D分别为列车在运行过程中的实际到、发时刻，则列车运行调整中的时间集为ψ={A0,D0,A,D}.

定义列车的优先级为λ，依据列车类型、等级来取不同的权重，M为足够大的正数.

定义3个0-1决策变量：列车在车站办理停站作业θij、列车过站次序Xi1,i2,j，列车优先级ηi1,i2.若列车i在车站j办理停站作业，则θij=1，反之θij=0；若列车i1比i2先通过车站j，则Xi1,i2,j=1，反之Xi1,i2,j=0;若列车i1优先级高于列车i2,则ηi1,i2=1,反之,ηi1,i2=0.

2.2 约束条件和目标函数

2.2.1 约束条件

为保证列车行车安全，需考虑8组约束条件，具体描述如下：

1)不同时列车到达间隔时间约束.

在单线区段，来自相对方向的两列列车在车站交会时，从某一方向列车到达车站时起至相对方向列车到达或通过该站时止的最小间隔时间为

TB≤M(1-Xi1,i2,j)+Ai2,j-Ai1,j

∀i1,i2∈Qt, ∀j,j+1∈Qs

(1)

式中：TB为不同时列车到达间隔时间.

2)列车发车时间约束.

若列车在车站办理停站作业，则发车时间不得早于图定时间.

∀i∈Qt, ∀j∈Qs

(2)

3)到发线约束.

车站到发线占用数不得超过车站的到发线总数.

∀i∈Qt, ∀j∈Qs

(3)

4)客货列车间隔时间.

M(1-Xi1,i2,j)+Di2,j≥Ai1+1

M·Xi1,i2,j+Di1,j≥Ai2,j+1

∀i1∈Qh, ∀i2∈Qk, ∀j,j+1∈Qs

(4)

5)区间运行时间约束.

当列车发生晚点时，可以通过区间加速方式实现正点运行，提高行车效率，但需要满足不同等级列车在区间的最小运行时间ttλ,K约束.

∀i∈Qt, ∀j,j+1∈Qs

(5)

式中：ttλ,k为不同等级列车在区间的最小运行时间.

6)列车作业时间约束.

部分列车在车站作业时间需满足车站的最小作业时间约束.

Di,j-Ai,j≥θij·tsλ,j

∀i∈Qt, ∀j∈Qj

(6)

式中：tsλ,j为不同等级列车在车站的最小作业时间.

7)站内越行约束.

当前行列车i1在到达车站j后对后续列车i2产生晚点传播时，若列车i1,i2到达j站的时间间隔满足两列车的最小间隔时间μ，且列车i2优先级高于列车i1时，可实现站内越行.

ηi1,i2·(Ai2,j-Ai1,j)2≥μ2

∀i1,i2∈Qt, ∀j∈Qs

(7)

式中：μ为两列车的最小间隔时间；λi1、λi2为列车i1、i2的优先级.

8)运行调整时间约束.

当前行列车出现早点或晚点情况并影响到后续列车时，运行调整时间为两列车最小列车间隔时间、实际到达时间与图定到达时间差值的最小值.

∀i∈Qt, ∀j∈Qs

(8)

式中：tad为列车运行调整时间.

2.2.2 目标函数

由于客、货列车混跑下存在列车不同等级的情况，高等级列车和低等级列车相比，调整的效益更大.以客、货不同等级列车在调度区间内总的偏离图定列车运行时间最少为目标函数

∀i∈Qt, ∀j∈Qs

(9)

式中：Z为目标函数；λ为等级权重.

旅客列车有三个等级：第一等级为直达特快旅客列车，最高速度为160 km/h；第二等级为快速旅客列车，最高速度为120 km/h；第三等级为普通旅客列车，速度为90～110 km/h.高等级的列车在运行调整时具有优先权.

3 算法设计

考虑到列车运行调整问题多、约束、求解复杂的特点，在线路长度和列车数量增多的情况下，求解难度呈指数级增长，需要现代启发式算法求最优解或近似最优解.因此，可以选择人工蜂群算法(Artificial Bee Colony,ABC)进行求解.具体算法步骤如下：

Step1 随机产生初始群体P即SN个初始解，SN为种群规模也等于蜜源数目，迭代次数iter=0，最大迭代次数MCN，初始化标志向量trial(i)，记录同一蜜源的连续开采次数.每个解Xi(i=1,2,…,SN)是1个D维向量，D为优化参数的个数，初始化后，由雇佣蜂、跟随蜂、侦查蜂对位置(解)进行改进的循环搜索过程.

Step2 在搜索过程中，雇佣蜂对蜜源邻域进行搜索，产生1个新蜜源位置(新解)为

υij=xij+ξij(xij-xlj)

(10)

式中：l∈{1,2,…,SN}；j∈{1,2,…,D}；且l≠i,υij为新蜜源位置；ξij为[-1,1]之间的随机数，当新蜜源位置比原蜜源位置更优时，则替换，反之则保留.

Step3 跟随蜂按照轮盘赌的选择策略来判断选择哪个蜜源，判断式为

Ci=fiti/(fit1+fit2+…+fitSN)

(11)

式中：Ci为选择概率；fiti为解Xi的适应度函数值.

Step4 若解Xi在“limit”次迭代后仍不能改良，则表示陷入局部最优解，该蜜源舍弃，对应的1个雇佣蜂变成侦查蜂，并由下式随机搜索1个新蜜源替换原蜜源：

(12)

ABC算法在蜂群位置更新上采用随机函数，存在收敛速度快、易陷入局部最优及搜索精度方面的问题，结合上述问题和列车运行调整的特点，从以下几个方面进行改进：

①算法初始化输入图定到、发时刻，实际到、发时刻，列车间隔时间，列车最小间隔时间，车站计划作业时间(涉及到时间均转化为分钟计算)，列车区间运行时间，车站到发线数目，各等级列车对应的权重，种群规模SN，最大迭代次数MCN，控制参数limit，根据列车实际运行时间和图定时间来确定晚点列车和站点，并初始化产生SN个满足约束条件(1)～(6)的随机解以提高求解效率.

②在蜂群的搜索寻优过程中，通过实际运行时间和图定时间对比,确定晚点时刻、待调整列车和站点，按约束条件(5)～(8)计算调整后列车到、发站时间，并对发车顺序进行调整，同时记录当前的最优解.

③在初始阶段，蜂群搜索进程快，步长较大，搜索范围广，在接近最优解范围时，需要精细搜索缩小搜索范围.根据需要，在搜索阶段引入自适应因子ω[13].在初始阶段ω值较大，扩大蜂群搜索范围，在蜂群接近最优解时ω较小，缩小搜索范围，调整式为

ω=ω-+(f-fmin)·(ω+-ω-)/(fa-fmin)

(13)

式中：ω+、ω-分别为最大、最小惯性权重；f、fa、fmin分别为当前适应度函数值、平均适应度函数值、群体最小适应度函数值.

则式(10)调整为

υij=xij+ω·ξij(xij-xlj)

(14)

④在蜜源位置更新阶段引入柯西分布算子，避免算法陷入局部最优解[14].若在蜜源更新阶段引入柯西变异算子，则采蜜蜂有可能跳出局部最优.一维柯西分布的概率密度函数为

f(x;0,1)=γ/[π·(γ+x2)]

(15)

当γ=1，x=0时称为标准柯西分布.

改进后侦查蜂的搜索公式，即式(12)变为

(16)

式中：C(0,1)为标准柯西分布.

自适应柯西变异人工蜂群(ACMABC)算法流程见图1.

4 计算实例与分析

以中国铁路昆明局集团有限公司2019年调整后的盘西铁路列车运行图相关资料为例进行分析.盘西铁路西起贵昆铁路沾益站，东经富源至红果与南昆线相接，向北沿长江至柏果，与水柏铁路相连，跨越云贵两省，区内煤炭资源丰富，全长136 km沿线途径10个站点，划分为9个区间.调整时段选某日5:00—19:00，按列车进入区段时间编号为i1,i2,…,i11，车站按沿途编号为j1,j2,…,j11，具体车次见表1.

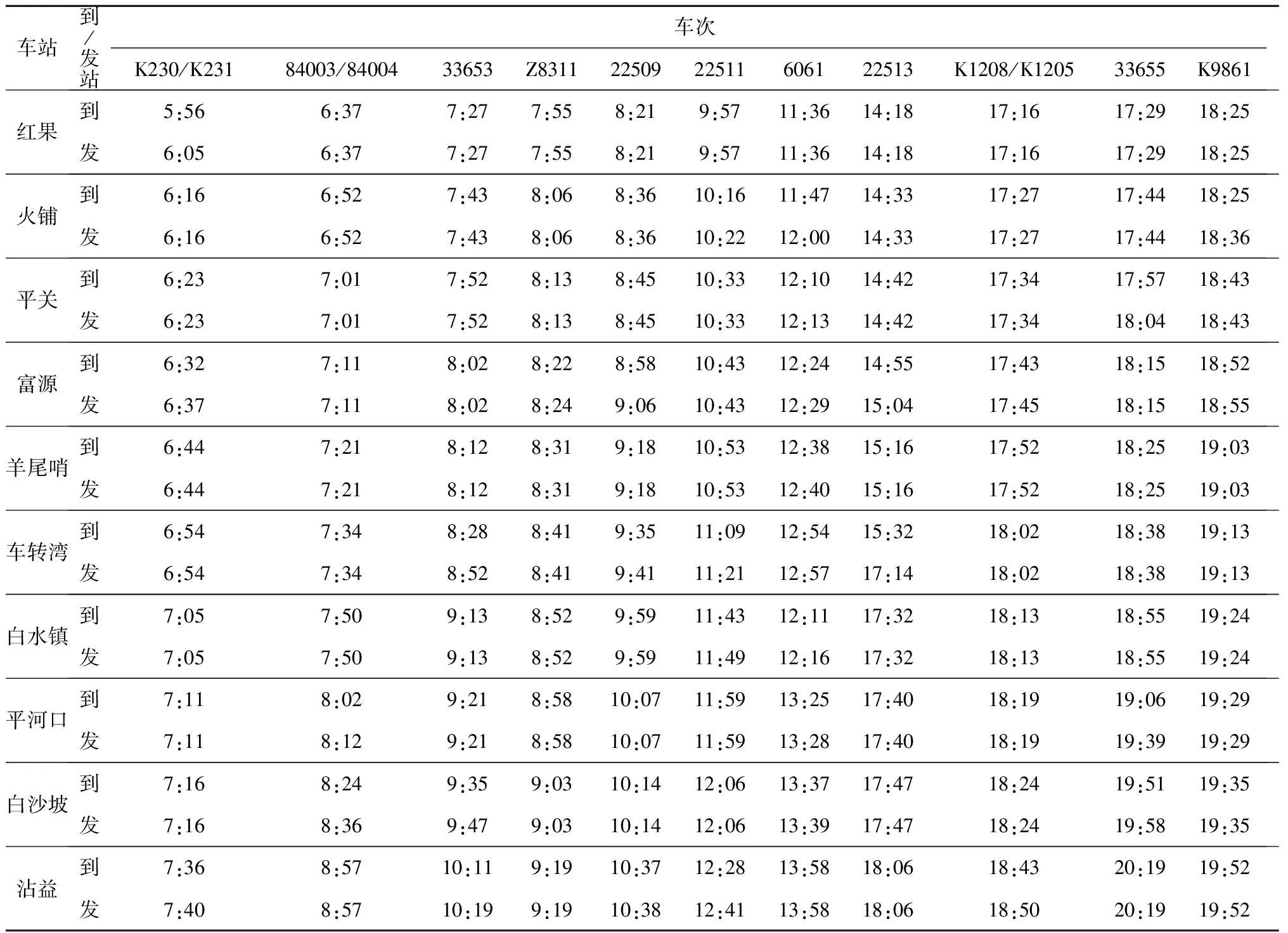
表1 盘西铁路5:00—19:00原列车时刻表

其中，速度160 km/h的列车为1列，速度120 km/h的列车为3列，速度90～110 km/h的列车位1列，货运列车为6列，列车等级为[2 4 4 1 4 4 3 4 2 4 2]，对应权重λ=[0.3 0.1 0.1 0.4 0.1 0.1 0.2 0.1 0.3 0.1 0.3]，M取值为1 440，车站的到发线数目、计划运行时刻表、停站情况、间隔时间、区间运行时间均由列车运行图技术资料给出.

为更好验证算法的有效性，采用电脑主频CPU为Intel(R)Core(TM)i5-7267U，内存为8.0 GB，Matlab2019a进行求解，设置受轻微扰动、较大扰动两个场景进行模拟，并计算对应的目标函数Z、运行时间.参数设置：最大迭代次数MCN=1 500，limit=200，SN=50，xmax=0.75，xmin=0.25.

在轻微扰动场景中，假设列车到站时发生4列列车初始晚点的情况：列车i1、i4、i7、i8分别到达站j3、j4、j2、j8各晚点37、10、20、50 min，初始晚点时间为117 min.在其他控制参数保持不变的情况下，MCN取不同的数值运行，所有计算均进行10次并取均值，得到ACMABC算法优化目标函数值见表2.

表2 ACMABC算法优化目标函数值

由表2可见：当迭代次数MCN较小时，ACMABC算法在对应目标函数的提升并不明显；随着迭代次数变大(MCN=1 500),ACMABC算法的有效性逐渐体现；随着迭代次数倍数增加(MCN=3 000),优化结果又趋于一致，过多的迭代次数耗费时间巨大，本文设计在有限的时间下进行列车运行调整.

根据文献[15]设计解的性能指标，本文算法求得的目标函数最优值Z,实际最优值为Ztrue，则解的性能指标值为

(17)

式中：Per为解的性能指标值，%.

性能指标值Per越小，则解越精确，不同参参数取值对算法性能的影响见图2.由图2(a)可见，随着limit值的增大，ACMABC算法性能呈上升后下降的趋势；当limit取值较大时，ACMABC算法产生的随机解个数较少，易陷入局部最优；当取值较小时，搜索能力不足，算法的性能下降.因此，必定有值(limit=200)能达到算法性能最优.

由图2(b)可见：随着种群规模SN增大，ACMABC算法求出的解呈现先下降后上升的趋势；当SN数值增大时，全局搜索能力变差；当SN降低时，影响蜂群的搜索能力；当SN=100时效果最好.

根据上述参数设置，对轻微扰动场景下的4列晚点列车进行自动调整，通过算法求出最后晚点总时间为147 min，并进行如下调整：列车i1在站j3到达晚点后，进行停站作业压缩、赶点运行，最终到站晚点28 min；列车i1晚点对站j3后续列车i2产生影响，满足列车在区间最短运行时间和车站最短作业时间下，列车i2到达站j9恢复正点运行.此外，列车i4、i7、i8最终晚点20、49、50 min；列车i9在站j8实现越行，即当低等级列车晚点引起高等级列车后效晚点时，高等级列车可以在车站越行通过以减少晚点传播时间.

算法的收敛曲线对比见图3.

由图3可见：ABC算法在0～260代之间，群体最小适应度速率增长快.当超过260代后，曲线趋于平滑，而ACMABC算法在接近220代时已趋于稳定；在运算时间上，ACMABC算法均耗时319 s, ABC算法需耗时360 s,这显示出ACMABC算法在全局搜索能力和收敛性上的有效性.在运行15次后，取15次的优化目标函数均值，ACMABC算法在平均优化目标函数值上较ABC算法减少58.5%，平均搜索次数减少33.2%，平均运行时间降低11.4%.

在较大扰动场景中，随机增加不同等级的晚点列车数目和晚点时间，计算受扰动下的目标函数值、运行时间T、迭代次数，运行10次并取均值进行比较，结果见表3.

表3 不同晚点情况下ACMABC算法与ABC算法求解结果比较

由表3可见：在受轻微扰动时，ACMABC算法在运行时间上缩短15.4%，在目标函数值上与ABC算法差值小；在面对较大扰动时，ACMABC算法求解效率增加了49.7%，运行时间减少了20.6%，而ABC算法未求得可行解.在2个场景下ACMABC算法的求解表明：本文设计的客、货混行条件下，列车运行调整模型和自适应柯西变异人工蜂群算法(ACMABC)具有有效性.

5 结论

1)考虑列车的优先级、到发时间、客货列车间隔时间、到发线等约束条件，以加权的总的偏离列车图定运行时刻最少为目标函数，构建客货混行条件下的列车运行调整模型.

2)针对人工蜂群算法易陷入局部最优、收敛效果差的问题，采用自适应柯西变异人工蜂群算法(ACMABC)，以盘西铁路全线某时段的列车为依据，模拟2个晚点场景并进行列车调整，通过计算证明设计的模型与算法在解决列车运行调整问题上具有有效性.

3)以单线铁路上客、货混行条件下列车运行调整为例进行研究，且晚点时间确定，复杂度较低.下一步的研究重点是考虑双线铁路不确定晚点时刻下的列车运行调整.