基于IPSO-BP的轻型汽油车道路排放预测

王志红，严 浩，袁 雨，刘志恩

(武汉理工大学 a.现代汽车零部件技术湖北省重点实验室,b.现代零部件技术湖北省协同创新中心，武汉 430070)

机动车数量持续增加，给环境和人体带来更多的危害，城市机动车又以轻型汽油车为主，加强对轻型汽油车排放的管理至关重要[1].受实际工况影响，试验室检测不能真实反映实际道路的排放水平[2].因此，便携式排放测试系统(PEMS)发展起来，安装在机动车上，其测量数据能够反映实际道路上的排放水平.国Ⅵ标准的实施，给机动车排放提出了更高的要求，基于此，建立一种轻型汽油车排放预测模型，不仅节约试验时间，还可减少因重复RDE试验的经济投入，具有一定的理论意义和工程价值.

国内外学者基于以上问题进行了大量研究，神经网络模型具有开发周期短、经济成本低和预测精度要较高等优点，但同时存在一些不足.文献[3]利用燃烧学仿真软件建立了中速柴油机的NOx排放预测模型，但存在建模方法复杂和计算过程慢的缺点，预测精度较差.文献[4-6]利用BP神经网络模型进行了排放预测，但由于汽车排放预测存在非线性、特性参数多的问题，导致预测误差较为明显.文献[7-8]在神经网络中分别加入偏最小二乘法和遗传算法对其进行优化，所建模型具有充分提取自变量信息的优点，同时对训练数据的需求小，但非线性拟合能力较差.文献[9]以BP神经网络为基础，引入LM优化算法，建立CO排放预测模型，仿真结果接近实测数据.文献[10]建立了多因素神经网络模型，并结合台架试验数据分析了各试验因素的重要度和试验控制性.

对于上述排放预测模型研究存在的问题，通过算法改进来提高模型的泛化能力，因此本文作者从符合国Ⅵ标准的轻型汽油车实际行驶排放(RDE)测试出发，以PEMS测得排放数据作为基础，在BP神经网络中加入改进粒子群算法(Improved Particle Swarm Optimization Algorithm，IPSO)，建立轻型汽油车排放预测模型.

1 RDE试验与数据

1.1 RDE试验基本要求

为了体现被测车辆的实际行驶排放，采用外部电源向PEMS提供电能，其中排气流量计与排气管相连接固定在车辆尾部，GPS和气象站固定在车顶；车载尾气分析仪SEMTECH-DS与电池组固定在后座.排气通过流量计后方的两个取样口送入分析仪中，记录数据并存储于数据卡，具体布置如图1所示.被测车辆为国Ⅵ 轻型汽油车，后处理形式为GPF/TWC，采用直喷的供油方式，其他参数：整备质量为1 850 kg、发动机最大功率为180 kW、排量为1.5 L.

参照《轻型汽车污染物排放限值及测量方法(中国第六阶段)》发布稿[11]，RDE试验持续90～120 min，试验工况包括市区、市郊和高速路段，其中市郊路况可以短暂出现市区路况，高速路况可以短暂出现市区和市郊路况，具体参数见表1.

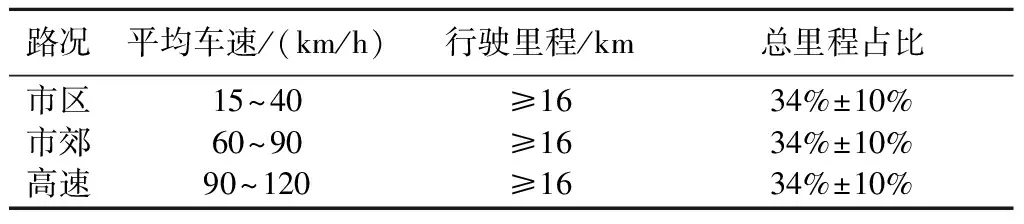
表1 试验工况属性

1.2 RDE试验基本流程

按照1.1将PEMS安装到试验车辆上，接通电源待预热完毕以后，对设备进行泄漏检查，对于气体分析仪采用两点标定，即用零气和量距气进行零点和量距标定.

测试设备在发动机第一次起动前开始记录数据，整个过程不间断记录污染物浓度、车辆位置、环境条件等，按照规定试验工况驾驶车辆，达到要求停止记录.分析仪长时间使用后会出现漂移误差，停止记录数据后检查设备的漂移情况，确保试验数据的准确性，检查方法与标定设备方法相同.

2 建立排放预测模型

2.1 试验数据前处理

由于测试模块之间的响应时间不同，对数据进行时序校准[12]，具体步骤如下：GPS和气象站通过车速与Silver Scan-Tool模块对正；Silver Scan-Tool模块和气体分析仪通过发动机转速和CO2浓度对正；气体分析仪和尾气流量计通过CO2浓度和排气流量对正，如图2所示.

除去车辆冷起动、车速为零及发动机熄火期间的数据，在余下数据中选出3 000组样本数据，为了提高所建立模型的泛化能力[13]，保证训练样本占绝大部分，将3 000组样本数据随机分成三部分：训练样本占80%、验证样本占15%、预测样本占5%.

2.2 主成分提取

为避免输入量过多，导致预测时间变长且精度降低，选取与影响排放较为明显的变量作为代入参数，同时考虑出现影响因素较多的情况，利用主成分分析进行降维，来作为预测模型的输入[14].车速V和加速度A对排放有很明显的影响，而发动机转速R及负荷率ES是改变车速和加速度的原因.排气温度T会对催化剂活性造成影响，从而影响排放，同时燃油消耗率B及排气流量F会对排放造成影响，故选择以上7个变量作为代入参数.

首先对7个参数进行标准化处理，使每个变量经处理后平均值为0，标准差为1，处理后的参数值为

(1)

式中：Xi为初始参数；E(Xi)为初始参数平均值；D(Xi)为初始参数标准差.

再对7个处理后的特征参数进行因子分析，计算得到特征参数之间的相关系数，并继续求解相关系数矩阵的特征值，按照由大到小的顺序排列，计算每个特征值的方差贡献率为

(2)

式中：λi为特征值.该矩阵共有7个特征值，求解结果如表2所示.

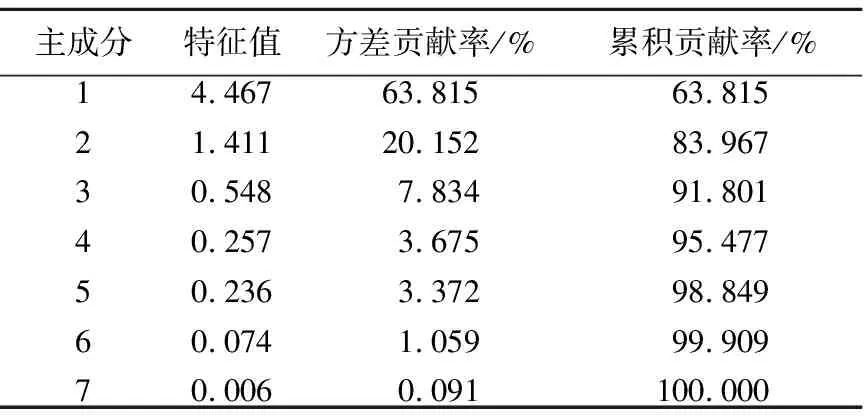
表2 主成分提取方差贡献率

一般来说，主成分分析要求提取的主成分方差累积贡献率达到80%以上才算合理有效.由表2可知，第3个特征值下方累积贡献率为91.801%，第4个特征值下方累积贡献率为95.477%，已经能够代表7个特征参数的绝大部分信息，即本次主成分分析共提取4个主成分，成分矩阵见表3.

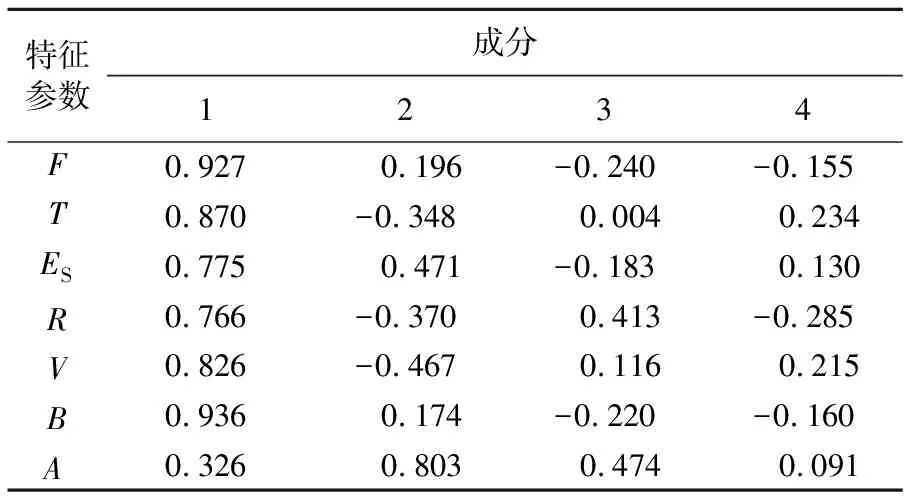
表3 成分矩阵表

由表3中数据可得到主成分特征向量为

F1=0.927Y1+0.87Y2+0.775Y3+0.766Y4+0.826Y5+0.936Y6+0.326Y7

F2=0.196Y1-0.348Y2+0.471Y3-0.37Y4-0.467Y5+0.174Y6+0.803Y7

F3=-0.24Y1+0.004Y2-0.183Y3+0.413Y4+0.116Y5-0.22Y6+0.474Y7

F4=-0.155Y1+0.234Y2+0.13Y3-0.285Y4+0.215Y5-0.16Y6+0.091Y7

表达式中F1～F4为主成分特征向量，将作为BP神经网络的输入信号；Y1～Y7为标准化处理后的特征参数.

2.3 神经网络架构选择

图3为典型三层BP神经网络架构，由输入层、隐含层、输出层组成.

其中：X=(x1,x2…，xn)T为输入层；Y=(y1,y2…，ym)T为隐含层，其层数根据实际问题需要来确定；Z=(z1,z2…，zt)T为输出层；V、M为各层之间的权值.

2.3.1 输入层及输出层确定

选取了车速V、加速度A等7个参数作为污染物排放影响因素，并对这些参数进行了主成分分析，得到4个主成分F1、F2、F3、F4，作为神经网络的输入层.对于输出层，本文对排放物进行预测，根据RDE相关法规，选择CO和NOx排放量作为输出.因此排放模型可简化为

(CO、NOx)=δ(F1、F2、F3、F4)

(3)

式中：δ为输入层到输出层的映射，与各层神经元之间的权重相关.

2.3.2 隐含层层数及节点数确定

理论上多隐含层神经网络非常适合于非线性系统的建模及控制，增加隐含层可以降低网络误差，但会使网络复杂化，增加网络训练时间和出现“过拟合”的倾向.本文选择双隐含层的神经结构，保证一定的泛化能力前提下减少训练时间.

隐含层节点数越多，网络易出现训练过度现象，泛化能力较差；节点数越少，网络不能很好的学习，达不到期望的预测值.根据相关研究[15]，对于第2隐含层，其节点数等于输出层节点数时，模型预测性较好.使用经验公式(1)、公式(2)与Kolmogorov公式(3)来确定第1隐含层节点数，并通过训练结果对比来确定最佳节点数.

(4)

(5)

Nhid=2Nin+1

(6)

式中：Nhid为第1隐含层节点数；Nin为输入节点数；Nout为输出节点数；α为1～10之间的调节常数.

选择部分排放数据对神经网络进行训练，结果如图4所示.

可以看出，隐含节点数为10时其训练误差最小.结合以上讨论，确定模型使用的BP神经网络架构为4-10-2-2.

2.3.3 模型传递函数选择

对于双隐含层BP架构，从输入层到输出层，共有3个传递函数.通过多次模拟结果对比，对输入层到第1隐含层选用logsim传递函数；第1隐含层到第2隐含层，以及第2隐含层到输出层选用purelin线性传递函数.

2.4 基于IPSO算法的BP模型

2.4.1 PSO算法及参数设置

标准PSO数学形式描述如下，每个粒子用xi=(pi,vi)表示，i=1,2,…,N：

1)时刻t=1，随机生成N个粒子，x(t)=(x1(t),x2(t),…,xN(t))计算粒子到目前为止经历的最优位置，记为粒子最佳位置pbest(t)；全局最优位置记为gbest(t).

2)时刻t=t+1，有

vid(t)=ωvid(t-1)+

c1r1[pbestid(t-1)-pid(t-1)]+

c2r2[gbestd(t-1)-pid(t-1)]

(7)

pid(t)=pid(t-1)+vid(t)

(8)

式中：vid(t)为t时刻粒子速度；pid(t)为t时刻粒子位置；ω为惯性权重；c1,c2为学习因子；r1,r2为0～1之间的随机数.

按式(7)及式(8)迭代粒子速度及位置，得到新的x(t).

3)如达到终止条件，结束搜寻过程，输出gbest(t)，否则转入上一步.

对于主要参数的设置，其中惯性权重为

(9)

式中：ωmax、ωmin为惯性权重最大值和最小值；fmin、fmean为当前群体目标函数最小值和平均值.

研究表明：c1、c2取值之和接近4时，算法表现出更好的性能，这里均取值为2；粒子数量定为40；极限速度vmax取1.

2.4.2 PSO算法改进

对PSO算法存在的两点问题[16]，进行了改进，改进后的PSO称为改进粒子群算法.

1)学习因子定为常数，在迭代的过程中寻优能力会逐渐降低，学习因子应在优化过程中随时间而变化，保证c1前期较大、c2后期较大的变化规律，计算方式改进为

(10)

(11)

式中：c1,fir为初始学习因子，此处取2.5；c1,end为停止寻优值，取0.5；c2,fir为初始学习因子，此处取0.5；c2,end为停止寻优值，取2.5；tmax为最大迭代次数，取100.

2)惯性权重会随着迭代而衰减，为保证正常的收敛速度，惯性权重应保持非线性衰减，使粒子速度降低较慢，计算方式改进为

ω=ωmax-(ωmax-ωmin)×

(12)

2.4.3 IPSO-BP模型建立

粒子位置和速度是一个a维向量，由BP神经网络中的阈值和权值组成.适应度函数由训练误差组成，在每一次迭代中，粒子映射到网络中去，通过训练误差确定适应度值，即

(13)

式中：f为适应度；f(xi)为网络理论输出；φi为网络实际输出；n为网格数量.

建立IPSO-BP预测模型，其参数为：粒子数量，40；终止迭代次数，100；初始学习因子c1、c2取值均为2；惯性权重ωmax、ωmin分别取0.8、0.4；极限速度vmax取1.

算法流程如图5所示.

3 模型预测结果分析

通过建立的IPSO-BP排放预测模型，将整理的试验数据按照前文要求进行分组，对模型进行训练、验证及预测，其中有150个预测样本，CO和NOx排放预测结果见图6和图7.

由图6和图7可知，在排放峰值附近，由于运行工况急剧变化及模型本身响应时间的限制，其预测值与试验值有一定的偏差，但从整体的排放趋势来看，可以认为预测结果能够较好的与试验值相吻合，其平均相对误差分别为10.58%和13.76%.所建立的IPSO-BP排放预测模型能够对轻型汽油车瞬时排放实现精度较高的预测.此外计算CO和NOx排放因子来衡量预测模型的总体排放误差，分别计算了市区、市郊和高速路的排放因子，并对结果进行加权，CO和NOx排放对比结果如表4所示.

表4 排放因子预测误差

可以看到，CO和NOx总排放因子平均相对误差分别为4.81%和6.4%，且预测值均小于试验值，是由于在排放波峰附近，发动机运行工况急剧变化，导致模型预测值要小于试验值，从而造成了这种误差.计算表明，误差大小都在可以接受的范围内，所建立的预测模型对轻型汽油车整体排放水平有较好预测性.

4 结论

1)对PSO算法提出了改进方法，保证学习因子在优化过程中随时间而变化；惯性权重应保持非线性衰减，使粒子速度降低较慢；改进后的算法表现出更好的性能.

2)基于IPSO-BP神经网络，结合RDE试验排放数据，利用主成分分析法对7个代入参数进行了降维，并以CO和NOx排放为输出，建立了某轻型汽油车的排放预测模型，对CO和NOx排放预测相对误差分别为10.58%和13.76%.

3)所建预测模型同样适用于车辆整体排放预测，CO和NOx排放因子平均相对误差分别为4.81%和6.4%.