考虑施工过程的土压平衡盾构喷涌预警研究

赵宗智，崔 明，荆 敏，赵伯明，王 潇,3，王子珺

(1.中交隧道工程局有限公司，北京 100102；2.北京交通大学 土木建筑工程学院，北京 100044；3.中国建筑股份有限公司，北京 100029)

土压平衡盾构工法近年来广泛应用于我国城市地下铁路的工程建设，而在高渗透性地层内施工时，由于水压控制困难，盾构机土舱及螺旋输送机内的渣土易形成集中渗流，往往造成喷涌灾害的发生.

目前国内外对喷涌灾害的研究主要集中于喷涌的防治和改良[1-3]，而针对喷涌发生机理和预警指标的研究则很少涉及.朱伟等[4]建立了土压平衡盾构压力舱、螺旋输送机整体模型，分析了喷涌发生的条件，其模型基于一维假设，未考虑盾构施工作用力引起的地层水压分布变化；戴轩[5]引入Ergun方程考虑水流的紊流效应，将地下水在土压平衡舱中运动表述为二维流动，但未考虑盾构施工荷载对地层孔隙水压力分布的影响.学者们对地层内超孔隙水压力变化及其规律进行了研究分析[6-7]，而只有少数研究考虑了施工过程的影响.魏新江等[8]运用应力释放理论及应力传递理论，推导了盾构施工引起周边土体任意位置的超孔隙水压力峰值的计算公式；丁智等[9]运用明德林解推导了半无限空间饱和土中基于盾构施工切口附加推力、盾壳摩擦力和盾尾注浆压力参数的土体内各点超孔隙水压力计算公式，而上述研究也均未提出明确的喷涌灾害预警指标.

本文作者首先分析盾构静止状态下渣土水头分布模型的局限性，进而提出建立考虑施工过程影响的渣土水头分布模型的研究方法，通过设计正交试验分析正面附加推力、刀盘中点埋深、地层弹性模量、地下水水位高度等因素对盾构开挖面超孔隙水压力的影响，然后基于理论解析和数值模拟推导盾构正面附加推力与开挖面超孔隙水压力之间的关系式，进而建立考虑施工过程的土压平衡盾构螺旋输送机的渣土水头分布模型，最后基于喷涌临界条件建立喷涌预警指标，以实现对盾构施工喷涌灾害风险的科学评估.

1 静止状态下渣土水头分布模型

研究喷涌问题的关键在于确定螺旋输送机出土口的水流流速以及水压大小，即水流在渣土中的流动状态，其实质是研究地下水在盾构机内部的渗流问题，通常可利用多孔介质中流体的渗流原理揭示喷涌的发生规律[4,10-11].为了确定地下水在盾构机内部的流动状态，需要建立渣土水头分布模型以推导出土口孔隙水压力的解析解，获得地下水在盾构机土仓、螺旋输送机的渣土内水头分布情况.

盾构静止状态下渗流的几何模型如图1所示，建立以螺旋输送机进土口处水平线为x轴，x轴与开挖面在土仓交点处为原点，通过原点铅垂线为y轴的坐标系.设定原点埋深为Z，原点处开挖面土体中地下水的水头为H1，位置水头为0，速度水头为0；出土口处水头为H2；土仓长度为L1，螺旋输送机长度为L2;θ为螺旋输送机与水平面的夹角.该模型展示了富水砂层中地下水在盾构机中的流动过程.

当盾构机静止时，假定刀盘掌子面的支撑力等于掌子面水土压力，不施加附加土压力，地层中不产生超孔隙水压力，则盾构静止状态下的土仓和螺旋输送机内水头分布为

(1)

式中：A1为土仓断面面积；A2为螺旋输送机断面面积；Q1为土仓出土口流量；Q2为螺旋输送机出口处流量；ξ为经验系数；g为重力加速度；a为比表面积；φ为岩土孔隙度；μ为流体运动黏度.又由流体质量守恒Q=Q1=Q2可得H2、H1和渗流量Q之间的关系式为

(2)

式中：K为土体的渗透系数.由一维渗流模型的定流量或定孔压边界条件，即可解得地下水在盾构机土仓、螺旋输送机渣土内的水头分布情况.由于实际施工过程中影响因素很多，盾构施工过程中到达开挖面时土体孔隙水压力较大，且正面附加推力是开挖面到达时孔隙水压力提升的主要原因[9].因此仅考虑静止状态下的水头分布模型不能建立反映盾构施工过程的准确喷涌预警指标.

2 正面附加推力与超孔隙水压力

基于流体在多孔介质内的渗流原理，首先分析盾构施工推进及地层条件等因素对开挖面超孔隙水压力的影响.在把握主要影响因素的基础上，结合解析公式与三维渗流数值模型，推导正面附加推力与开挖面超孔隙水压力间的关系式，为建立考虑施工正面附加推力影响的水头分布模型，评价喷涌的临界条件和预警指标提供理论依据.

2.1 开挖面超孔隙水压力的解析计算方法

基于弹性假设比奥固结理论的正面附加推力的解析解[9]，建立考虑正面附加推力的盾构施工解析模型如图2所示.图中，z0为隧道轴线埋深，单位为m；R0为刀盘半径，单位为m.

在正面附加推力作用下，O-xyz坐标系中任意点(x,y,z)的土体超孔隙水压力表达式为

(3)

(4)

其中，

(5)

式中：Pq为正面附加推力引起的土体超孔隙水压力，单位kPa；qt为正面附加推力，单位kN/m2；r为监测点与刀盘圆心距离，单位为m.

由式(4)可知，正面附加推力的影响可转化为刀盘前方位置地层孔隙水压力的提升，该式以比奥固结理论为基础，本身仅针对饱和土解，考虑的自变量为盾构施加的附加土压力大小、盾构机半径、盾构机埋深，无法考虑到实际工程中地层泊松比、弹性模量等参数变化的影响，考虑将该解析式结合数值模拟方法开展研究，以得到更贴近工程实际的结论.

2.2 施工因素对开挖面超孔隙水压力的影响分析

为全面研究施工因素对地层超孔隙水压力的影响，通过设计正交试验进行分析.选择某地铁工程实例，采用数值分析方法进行有限模型建模与分析.盾构机刀盘半径为6.48 m，地层为砾砂层，泊松比0.24，密度1 800 kg/m3.

依据超孔隙水压力的发生机理确定关键影响因素的附加推力、刀盘中点埋深、地层弹性模量、地下水水位高度为研究对象，结合实际工程条件，考虑正面附加推力为20、40、60 kPa，刀盘中点埋深为12、17、22 m，地层弹性模量为20、30、40 MPa，地下水水位为-3、-6、-9 m等指标，设计了四因素三水平的正交试验，各因素水平见表1.

表1 正交试验参数

数值分析模型见图3，尺寸为40 m×40 m×45 m，隧道开挖长度为30 m，整个模型包括113 034个单元，63 775个节点，采用流固耦合模式，土体四周孔压固定，底部不透水，不考虑地层孔隙水向刀盘方向的渗流，仅允许正面刀盘位置点自由移动，通过改变正面支护力大小模拟正面附加推力大小.

将施加荷载后各监测点的孔隙水压力峰值作为正面附加力作用下的超孔隙水压力，通过计算所得的各监测点超孔隙水压力如图5所示.

由超孔隙水压力的数值模拟值分布结果可知，各模型的不同监测点均出现超孔隙水压力，同一模型各监测点的超孔隙水压力十分接近，不同模型各监测点的超孔隙水压力存在较大差异.

选用刀盘中点位置监测点(即监测点0)的超孔隙水压力峰值作为基准，可分析把握刀盘位置地层超孔隙水压力规律.运用SPSS软件分析不同因素对刀盘中点超孔隙水压力的影响效果，得到超孔隙水压力与正面附加推力、刀盘中点埋深、地层弹性模量、地下水水位高度等因素的影响关系，见表2.

由表2可知，刀盘中点埋深、地下水水位的显著性大于0.05，其对超孔隙水压力影响不明显，剔除后二次分析得到超孔隙水压力与正面附加推力、地层弹性模量的影响关系，见表3.

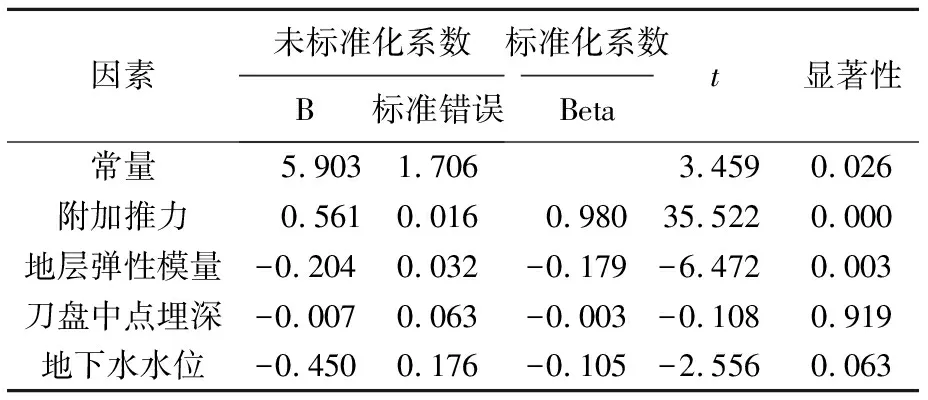
表2 四因素的SPSS多元线性关系分析结果

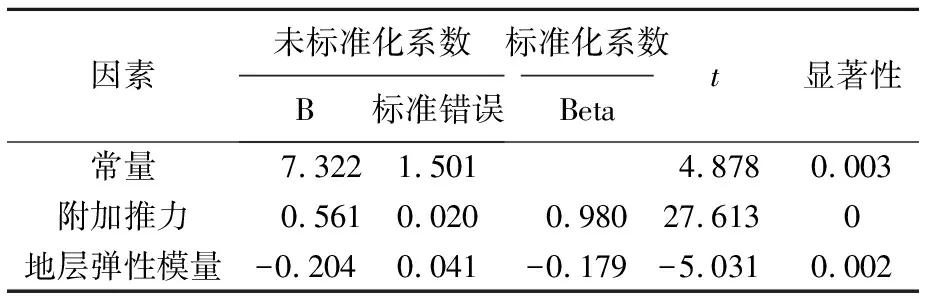
表3 两因素的SPSS多元线性关系分析结果

通过分析可知，盾构隧道埋深、地下水水位高低对超孔隙水压力大小的影响不显著，而正面附加推力的大小是超孔隙水压力大小的决定性因素.基于分析可以建立正面附加推力和地层弹性模量与超孔隙水压力间的关系式为

Pq=7.322+0.561qt-0.204E

(6)

式中：E为地层弹性模量，单位MPa.

(2)回填土采用3∶7灰土，分层铺摊，每层铺摊后随之耙平，铺土厚度为200～250 mm；采用压路机压实，压实系数应≥0.96。

同样，将表1中各模型试验参数带入解析计算式(4)，得到各监测点的超孔隙水压力值如图6所示.由图可知，各模型通过解析公式所得同一模型各监测点的超孔隙水压力结果十分接近，与采用数值模拟计算得到的结论一致.同样选取刀盘中点位置(即监测点0)的超孔隙水压力为典型位置，可对刀盘前方地层的孔隙水压力变化进行分析.

基于数值模拟和解析计算的结果可知，超孔隙水压力仅与正面附加推力和地层弹性模量相关，而解析计算式(4)中不含地层弹性模量，因此将正面附加推力单独分离，导入推力附加系数ψ，推导正面附加推力与超孔隙水压力的关系式为

(7)

Pq=ψ·qt

(8)

根据建立的公式计算各模型监测点0的推力附加系数ψ，结果如图7所示.可以看出，基于不同模型的推力附加系数趋于一个常数，其值约为0.485.通过导入推力附加系数ψ的概念，可在开挖面超孔隙水压力求解时直接按式(8)进行大幅度的简化计算，并为建立考虑施工过程的渣土水头分布模型提供了条件.

3 考虑正面附加推力的分布模型

由数值模拟与解析计算的结果可知，开挖面超孔隙水压力主要受正面附加推力控制，二者间关系如式(8)所示.在施工过程中，当刀盘前方出现超孔隙水压力时，地下水水头相应增大，地下水在螺旋输送机中的渗流状态随即改变，因此，静止状态下的渣土水头分布模型不再适用，需要建立考虑正面附加推力的渣土水头分布模型.

将式(8)代入伯努利方程可得

(9)

式中：γw为水的容重，单位为kN/m3.则存在正面附加推力qt时，可求得压力仓内水头h1和螺旋输送机内水头h2分别为

(10)

L1≤x≤L1+L2cosθ

(11)

在整个渗流路径上

(12)

式(10)～(12)即为考虑正面附加推力的改良渣土渗流水头分布模型.取螺旋输送机出土口的孔隙水压力为u2，则由图1模型几何关系及伯努利方程得

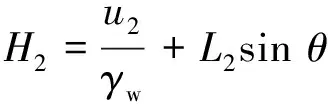
(13)

将式(12)代入式(13)得螺旋输送机出土口的渗流边界关系式为

(14)

在渗流量已知的情况下，由式(14)可求得开挖面处的孔隙水压力u2的大小，并由此建立判断喷涌风险的预警指标.

4 喷涌临界条件与预警指标

4.1 喷涌临界条件的确定

为了定量判断喷涌发生的可能性及程度大小，需要确定喷涌发生的定量边界条件[4].结合国内外相关工程案例，通过分析发生喷涌时对正常施工的影响，并考虑正常掘进速度下的渣土输水量后，定义排土口渗流量Q和水压力Pw为喷涌是否发生的两个判定指标.判定指标的大小和判别规则如图8所示，一般可认为排土器自身的压缩效应和排土闸门可抵抗10 kPa的水压力和3 cm3/s的渗流量.若渗流量Q和水压力Pw二者中任一指标低于判定值，则认为不会发生喷涌；若两者同时超出判定值，则视为喷涌发生；若排土口渗流量Q>4 cm3/s且水压力Pw>20 kPa同时出现，则认为发生严重喷涌.

4.2 基于渣土水头分布模型的喷涌预警指标建立

基于本文建立的渣土水头分布模型和喷涌临界条件可得到出土口的孔隙水压力表达式，假设轻微喷涌临界状态下螺旋输送机出土口渗流量Qqw=3 cm3/s，则出土口孔隙水压力的喷涌临界值uqw=10 kPa，出土口孔隙水压力越大，喷涌风险越高，见图9.

图9中a、b、c三条线分别代表了三种不同的渗流状态，状态a与喷涌区不相交，无喷涌风险；状态b、c与喷涌区相交，有喷涌风险.状态a、b、c的孔压-流量曲线分别与Qqw=3 cm3/s相交于不同点，交点的纵坐标Pw值越高，喷涌风险越大.

在水头不变的情况下，水流速度、孔隙水压力会随着出土口物理条件的变化而发生转变，因此若预警值达到喷涌发生临界值，可通过调整螺旋输送机出土口闸门的状态使水流呈现高流速-低孔压或低流速-低孔压状态以降低危害性喷涌发生的可能性.

由式(14)可得螺旋输送机出土口孔隙水压力u2，代入喷涌临界条件得

(15)

即当出土口流量Qqw=3×10-6m3/s时，发生轻微喷涌.临界水压力uqw为10 kPa.若u2>uqw，则具有轻微喷涌风险，且u2越大，喷涌可能性越高.

为使预警指标简明，定义轻微喷涌临界指标F1为

(16)

则当F1>0时，轻微喷涌可能发生，F1越大，发生喷涌的可能性越高.

同理，可定义严重喷涌临界指标F2，见图10.

假设轻微喷涌临界状态下螺旋输送机出土口渗流量Qyz=4×10-6m3/s，则出土口孔隙水压力的喷涌临界值uyz=20 kPa.若u2>20 kPa，则具有严重喷涌风险，出土口孔隙水压力u2越大，喷涌风险越高.

类似地定义严重喷涌预警参数F2为

(17)

当F2>0时，说明盾构施工存在严重喷涌风险，F2值越高，发生严重喷涌的可能越大.

5 结论

1)分析把握了附加推力、刀盘中点埋深、地层弹性模量、地下水水位高度四个因素对螺旋输送机渣土水头分布的影响.研究表明盾构隧道埋深、地下水水位高低对超孔隙水压力大小的影响不显著，而正面附加推力的大小是开挖面超孔隙水压力大小的决定性因素.

2)建立了考虑施工正面附加推力影响的渣土水头分布模型.通过解析公式和数值模拟推导了正面附加推力与开挖面超孔隙水压力间的关系式，并建立了水头分布模型.

3)基于喷涌临界条件建立了轻微喷涌和严重喷涌的预警指标F1和F2.当F1>0时认为存在轻微喷涌风险，F1值越大喷涌风险越高；当F2>0时认为存在严重喷涌风险，F2值越大喷涌风险越高.