TI介质中qP波方程逆时偏移技术的研究现状与展望

何兵寿,武雪峤,高琨鹏

(1.中国海洋大学海底科学与探测技术教育部重点实验室,山东青岛266100;2.青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室,山东青岛266071)

各向异性理论的研究始于19世纪50年代[1],但早期的研究工作主要由数学物理学家主导,其应用范围也局限在晶体光学和晶体弹性方面。1911年,RUDZKI[2]强调了地震各向异性的重要性并第一次实现了各向异性弹性波的定量计算。随后该领域的研究进入停滞期,直到20世纪50年代,人们才开始研究地震各向异性对勘探地震的意义[3-9],在这个时期取得的主要成果包括:各向异性介质中地震波垂向和横向传播速度不一致的原因[4]、薄互层组合各向异性的产生机理[5]、方位各向异性的提出[6]、横波分裂现象的发现[7]与观测[8]及各向异性本构方程的建立[9]等。

从20世纪80年代起,地震各向异性的研究进一步细化,开始针对不同类型的各向异性介质展开研究,并提出了许多现在仍然广泛应用的理论。其中,最具代表性的是THOMSEN[10]提出的基于弱各向异性假设利用5个新参数描述横向各向同性(TI)介质中纵、横波的各向异性特性的理论,这5个参数分别为:vP0,vS0,ε,γ和δ,前两个参数代表P波和S波在对称轴方向的速度,后3个参数统称为THOMSEN参数(无量纲),分别代表纵、横波的各向异性强度和纵波的变异系数。由于这5个参数具有更直观的物理意义且便于应用,因此,该表征方式一经提出就受到了高度关注。

THOMSEN的工作是各向异性理论与技术的有力推动,几十年来,业界在各向异性领域开展了大量的研究工作并取得了诸多成果。主要包括各向异性地震波场模拟方法、横波分裂和纵横波慢度的研究、快慢横波的提取方法、裂缝或各向异性参数反演方法、TI介质中准P波方程的推导以及准P波或弹性波各向异性叠前偏移方法等。其中:叠前偏移技术是各向异性地震勘探领域的关键技术之一,理论上说,地震波的高精度叠前偏移不仅能实现地下构造的准确成像,而且能为叠前反演提供准确的共成像点道集。因此,业界对此项技术的研究尤为重视。

TI介质模型是当前最具代表性和应用潜力的各向异性理论,本文中的分析与论述仅限于该类介质。TI介质中纵波的偏振方向一般不与其传播方向平行,横波的偏振方向一般不与其传播方向垂直,因此它们都不是严格理论意义上的纵波与横波,但又具有与理论纵、横波相似的物理性质,因此称为准纵(quasi-P,qP)波和准横(quasi-S,qS)波。由于TI介质中qP波和qS波是耦合在一起的,不存在理论严谨的qP波方程和qS波方程,因此,只有采用弹性波方程对三分量数据进行地震各向异性逆时偏移才具有理论的严谨性。目前地震勘探工作仍以单分量纵波勘探为主,许多探区缺乏三分量地震数据,工业界迫切需要一种能够解决单分量qP波成像问题的逆时偏移方法,该需求推动了TI介质中qP波方程逆时偏移技术的产生和发展,具体思路为:在一定的假设条件下,对TI介质中的弹性波方程进行简化与推导,得到TI介质中的近似qP波方程,并由此结合逆时偏移的基本思路实现TI介质中的qP波逆时偏移。

本文主要分析当前基于TI介质理论的qP波逆时偏移技术,首先给出TI介质中qP波方程逆时偏移的基本流程,然后分析该流程中各个环节的研究现状和存在的主要问题,并给出下一步研究建议。

1 TI介质中qP波方程逆时偏移的实现思路与基本流程

TI介质中qP波方程逆时偏移一般通过数值求解各成像点的炮点波场和接收点波场,并利用时间一致性原理对炮、检波场进行互相关来实现,典型的计算流程如图1所示。

图1中各向异性参数建模不属于本文讨论范围,炮记录为采集得到的单分量单炮记录,其它黑框部分是中间结果,红框部分组成了整个TI介质中qP波方程逆时偏移技术体系,本文只论述红框部分的各个环节。qP波方程是逆时偏移的理论基础,激发源设置方法、qP波方程的数值解法、吸收边界条件和随机边界组成qP波方程正向和逆时延拓技术;波场传播方向优选、偏移噪声压制、成像条件应用和波场拉伸校正组成波场成像技术。本文对TI介质中qP波逆时偏移研究现状的分析也从这3个方面展开。

图1 TI介质中qP波方程逆时偏移的计算流程

2 TI介质中qP波方程的研究现状

TI介质中的qP波方程一般由具有垂直对称轴的横向各向同性(transversely isotropic media with vertical symmetry axis,VTI)介质中的qP波方程进行坐标旋转得到。VTI介质中qP波方程的推导主要有弱各向异性近似[10-12]和声学近似[13-21]两种思路。弱各向异性近似的研究源于THOMSEN[10],他假定3个THOMSEN参数均远小于1,然后对VTI介质中的qP波相速度表达式进行泰勒展开并只保留线性项,得到弱各向异性近似下的qP波相速度,再利用相速度与频率波数之间的关系公式得到弱各向异性近似频散关系方程,将其变换到时间域即可得到VTI介质的qP波方程。TSVANKIN等[11-12]得到了与之相同的结果。

声学近似的研究始于ALKHALIFAH[13-15],他假定沿对称轴方向的横波速度为零,然后利用VTI介质中的精确频散关系得到声学假设条件下的频散关系式,最后经过傅里叶反变换得到VTI介质中的qP波方程,再对该方程进行坐标旋转得到TI介质中的qP波方程。ALKHALIFAH方程是一个同时包含时间和空间四阶偏导数的偏微分方程,方程中还存在混合偏导数项,不便于求解与工程应用。为解决此问题,学者们通过引入不同的辅助函数对该方程进行了降阶处理[16-21],将其转换为更容易求解的二阶方程组,比较典型的方程主要有:ZHOU提出的方程[16]、DUVENECK等提出的方程[18]、FLETCHER等提出的方程[20]和KANG等[21]提出的方程,这些方程均可以较好地描述TI介质中qP波的运动学特征。

沈铭成的研究[23]表明,对于各向异性介质qP波,ALKHALIFAH声学近似假设的精度明显高于弱各向异性近似。因此目前业界倾向于采用声学近似方程解决TI介质的qP波偏移问题。但是声学近似的qP波方程存在以下缺陷:①存在菱形伪横波干扰(图2中黑色箭头所指处);②当THOMSEN参数δ>ε时难以稳定求解;③当对称轴倾角急剧变化时,方程不能稳定求解[22]。

图2 由ZHOU提出的方程得到的TI介质中的波场快照(ε=0.3,δ=0.1,θ=45°)

上述伪横波干扰不是TI介质的地震响应,而是方程本身的误差解,该误差会给逆时偏移带来假象并产生严重的数值频散问题(图2中红色箭头所指处),在偏移过程中必须压制。目前的压制思路主要有:①依据伪横波的产生机理,在数值求解过程中采用适当的方法进行压制[14,22-25];②推导不存在伪横波干扰的纯qP波方程[26-33]。第一种思路不改造方程本身,只在数值求解过程中采用适当方法压制伪横波,主要有各向异性介质参数匹配法[14,24]、波场滤波法[25]和辅助波场压制方法[22]等。第二种思路侧重从方程的角度解决问题,通过推导纯qP波方程来消除伪横波干扰,由于方程只存在qP波解,伪横波干扰自动消除。

VTI介质中纯qP波方程的推导思路总结为:首先用一阶泰勒展开式近似表示VTI介质精确相速度公式中的平方根项,得到相速度近似公式,然后由此得到VTI介质中qP波的频散关系式,最后利用该频散关系得到不同形式的纯qP波方程。如对该频散关系等式的两边同时乘以等式右边的分母项并进行时间和空间方向的傅里叶反变换,得到一个四阶的偏微分方程[33],或者通过引入辅助变量将其转化为一个二阶偏微分方程组[26,34]。也可以对频散关系式只进行时间方向的傅里叶反变换得到时间波数域方程,然后用伪谱法求解。但这样得到的方程分母项中包含了各向异性参数,不利于伪谱法求解,HARLAN[35]将相速度公式的分母项中所包含的各向异性参数舍去,得到相速度的HARLAN近似式,并进一步得到纯qP波方程。由于HARLAN近似式存在较大误差,郭成锋等[36]对该近似式进行了修正,在非椭圆项前添加了一个与ε有关的修正系数,得到了3种改进型HARLAN公式,并以近似精度最高的改进式为基础推导了TI介质纯qP波方程。此外、黄翼坚等[32],杜启振等[26]和ZHAN等[27]均利用不同的近似方法推导了TI介质纯qP波方程,这些方程都能在运动学上较好地拟合TI介质中qP波的传播过程,且不存在伪横波干扰,但许多方程中存在分数形式的伪微分算子,增加了求解的难度与计算成本。

为克服上述局限,XU等[30]通过在各向同性介质声波方程中加入一个标量算子实现对相速度的控制,并由此导出VTI介质的纯qP波方程,该方程的优点是能在各向异性参数δ>ε情况下稳定求解,缺点是描述的相速度只在波前面梯度的方向与VTI介质相速度相符,在其它方向则存在明显误差,当ε较大时,这种相速度的误差会导致波前能量分布的不均衡并产生噪声。XU等[30]进一步对该方程进行了改正,他通过在声波方程的空间微分项中加入各向异性参数,使方程的相速度曲线更接近VTI介质实际相速度,改进后方程的相速度不仅在波前面的传播方向上与VTI介质的相速度相等,在其它方向上也更准确,且不存在波前能量分布不均问题。ZHANG等[37]和张建敏[38]以该方程为基础,通过投影变换将该方程推广至TTI介质。ZHANG等[37]提出的TI介质纯qP波方程波前能量分布均匀(图3),不存在伪微分算子,结构简单,便于求解。张建敏[38]还通过引入辅助变量得到TI介质中的一阶纯qP波方程,该方程能够采用旋转交错网格有限差分技术求解,且相同条件下,一阶方程的计算精度高于二阶方程。

图3 由ZHANG等[37]提出的方程得到的TI介质中的波场快照(ε=0.3,δ=0.1,θ=45°)

3 TI介质中qP波方程的延拓方法

本节主要介绍qP波方程逆时偏移中的激发源设置方法、qP波方程的数值解法、吸收边界条件和炮点波场重构策略等方面的研究现状。

3.1 激发源设置方法

逆时偏移成像一般通过炮点正向延拓波场和接收点逆时延拓波场的互相关来实现,其中炮点波场的计算需要给定各向异性参数模型和震源子波,震源子波的类型、形态、主频以及频宽等决定炮点波场的诸多属性,炮点波场的属性又会影响逆时偏移的成像结果。不合理的震源子波会弱化炮点波场与接收点波场之间的相关性,降低成像准确性和分辨率[39]。因此,设置合理的震源子波是获取准确逆时偏移成像结果的前提。但相对于qP波逆时偏移领域的其它技术,激发源设置方面的研究相对滞后,特别是震源子波对逆时偏移的影响机理尚未明确,许多工作只得到了一些感性认识,未上升到理论高度。

目前,业界在该领域的研究主要集中在理论子波的特性分析方面[39],而实际地面记录的炮点子波远非理论子波,将震源子波设置成理论子波不合适,而设定为野外近源道记录的子波或激发震源的理论子波则会给逆时偏移带来严重的频散问题,并降低偏移剖面质量。因此,刘学义[39]直接从实测资料中提取子波并将其设置为震源子波进行逆时偏移,这种思路可以降低由于震源子波与记录子波不一致时对偏移结果的影响,它比直接将震源子波设置为理论子波更具合理性。问题的关键是如何从炮记录中提取出子波,目前大都采用反演领域或其它处理技术中的子波求取方法提取逆时偏移子波[40-41],还未见到针对qP波逆时偏移这一特定问题研发的子波提取技术。

3.2 qP波方程的数值解法

qP波方程的数值求解方法很多,每种qP波方程都有对应的求解方法。归纳起来,主要包括有限差分法、伪谱法以及有限差分与伪谱法的混合法3种,而有限差分法又包括交错网格法、旋转网格法、旋转交错网格法和紧致交错网格法等,几乎每种各向同性领域的波动方程数值求解技术都可以直接或稍加改动后用于解决qP波方程的数值求解问题。关于qP波方程的数值求解问题已有多人加以综述[42-43],本文不赘述。

3.3 吸收边界条件

接收点波场逆时延拓过程中,需要采用边界条件来压制计算边界的伪反射。目前常用的边界条件有:①基于单程波方程的吸收边界[44-45]。这类方法用拟微分算子分解波动算子并只保留向外传播部分,然后用Pade近似得到不同精度的边界微分方程,其效果取决于边界微分方程的精度,已有的低阶单程波方程均只能在小入射角前提下取得良好近似,当入射角较大时方程存在明显误差。提高单程波方程的阶数可以减小这种误差[46],但会增大算法复杂度和计算量,同时带来稳定性隐患。②基于波场衰减的吸收边界[47-48]。这类方法通过对边界附近的波场进行衰减消除边界反射,其效果取决于衰减函数的选择,模型复杂时很难找到一个合理的衰减函数。③基于完全匹配层(Perfectly Matched Layer,PML)技术的吸收边界条件[32-37,49-53]。此类方法的基本思路为,在计算区域周围设置吸收衰减带并沿坐标轴方向分解波场,在不同边界区域按照不同方式对分解后的波场进行衰减,达到消除边界反射的目的。

PML边界条件最早出现于电磁波模拟领域[49-50],随后被引入地震波数值模拟与逆时偏移领域[32-37,51-53],之后许多研究工作拓展了PML的使用范围[52-56],目前该边界条件已成为TI介质qP波逆时偏移领域应用最为广泛的边界处理方法。张岩[52]将一个二阶qP波方程变换到频率域并进行坐标变换,在频率域对波场进行分裂处理,然后逆变换至时间域得到该方程的二阶PML边界条件并在模型数据的qP波逆时偏移中取得了良好效果。黄建平等[53]给出了TI介质一阶速度-应力qP波方程的PML边界条件,在交错网格中推导了该边界条件的高阶有限差分格式并用模型数据加以验证;ZHANG等[37]推导出了二阶纯qP波方程的PML吸收边界及对应的有限差分格式,此算法能够很好地吸收TI介质中入射到截断边界的外行波,ZHANG等[37]还给出了TI介质中一阶纯qP波方程的PML吸收边界条件,该边界条件同样具有良好的外行波吸收性能。

3.4 炮点波场重构策略

地震波逆时偏移常采用以计算换存储的思路降低临时文件存储量和硬盘读写量,即进行两次炮点波场延拓,第一次延拓时存储部分波场信息,然后利用这些信息对炮点波场进行逆时重构。与此同时,接收点波场的逆时延拓也并行处理,这样就能实现炮点和接收点波场的同步延拓,避免逆时偏移过程中的临时文件存储和读写工作,发挥并行计算机的计算优势,提升偏移效率。

目前的炮点波场重构方法主要有4种:①基于检查点技术的重构方法[54],在正传过程中每隔一定时间间隔设置一个检查点并储存该点波场,反传过程中从检查点出发通过反复递推重构任意时刻的波场;②基于抽样插值法的重构方法[55],在满足采样定理的前提下对正传波场进行规则抽样,并通过数据压缩算法对抽样波场进行存储,采用适当的插值方法对信号重采样,插值重构任意时刻的有效边界层波场,通过最后两个时刻波场的反传并加入插值得到的有效边界层重构炮点波场;③基于有效边界存储的波场重构方法[56-58],该方法存储每次正传波场的四周有效边界层,并利用最后两次时间采样的波场做逆时传播,将每个时间采样点对应的有效边界加入反传波场中从而重构出该时间点的炮点波场值;④基于随机边界条件波场重构方法[56-60],在计算区域外设置随机弹性参数层,炮点波场正向延拓时记录下最后若干时刻所有网格点的波场值,并以该波场值为初始条件,进行炮点波场的逆时重构。

前3种方法一般结合吸收边界实现炮点波场重构,具有较高的计算精度,能够很好地解决二维偏移问题,但在三维情况下,受计算机内存限制,这些信息都必须存储到硬盘中,频繁访问硬盘不利于发挥并行机的计算能力优势,因此,前3种策略很难用于解决三维逆时偏移问题。随机边界策略能够避免频繁访问硬盘,但不合理的随机弹性参数无法完全破坏人工边界反射波场的相干性,致使随机边界产生的噪声对接收点附近地层的成像产生严重影响[57]。因此,边界处随机弹性参数的构造方式是随机边界策略的核心技术。

解决这一问题的代表性思路是利用随机介质模型构建随机边界[61-65],该随机介质模型由大、小两种尺度的非均匀介质组成,大尺度非均质介质是模型的均值速度,小尺度非均质介质是加在均值速度上的随机扰动。基于这种思路,奚先等[64]根据随机过程的谱分解定理,给出了一种利用局部自相关函数构造非平稳随机介质模型的方法,陈可洋等[65]则利用改进的混合型自相关函数构建各种尺度因子条件下的多层随机介质模型,张丽美等[66]基于自相关函数类型、相关长度和速度扰动标准差3个参数描述的随机介质表达方式构建参数化的随机边界,并通过模型试验给出了3个参数的取值原则。此外,SHEN等[67]采用形态随机的大尺度随机速度颗粒构建随机边界,实现了对随机边界散射波场低频分量的压制。

上述思路在各向同性声波方程的随机边界构建方面取得了效果,但由于TI介质的qP波方程包含多个弹性参数,这些弹性参数共同决定方程数值求解的稳定性,各向异性参数的微小波动极有可能引起各向异性视速度的很大波动,使偏移过程发散。因此,TI介质qP波方程随机边界构建中各参数的随机值设置是相互影响的,不能简单套用各向同性声波方程的随机边界构建方法,而应当针对qP波方程逆时偏移这一特殊问题,研发具有完善理论的随机边界弹性参数赋值方法。刘国峰等[68]在这方面进行了尝试,对比分析了3种随机参数设置方法,即:边界外扩区域的各弹性参数互不影响,独立处理;外扩区域设置为各向同性区域和外扩区域设置为均匀各向异性区域。认为将外扩区域设置为均匀各向异性区域能取得最优的模型数据成像效果。刘国峰等[68]将各弹性参数的随机设置作为一个整体对待,其研究思路具有很强的针对性和理论严谨性,但未给出各个参数的具体设置方法,故将各弹性参数组合为数组,在一定的约束条件下产生随机数组,并以该数组实现qP波逆时偏移随机边界的设置或许是一种可行的解决方案,但目前业界还缺乏这方面的研究工作。

4 TI介质中qP波方程逆时偏移的波场成像方法

本节主要介绍qP波方程逆时偏移中的成像条件、偏移噪声压制、波场传播方向求取和波场拉伸校正等方面的研究现状。

4.1 成像条件

地震波逆时偏移领域常用激发时间成像条件、互相关成像条件和能量比成像条件等对地震波场进行成像。其中激发时间成像条件无法解决多路径情况,速度场复杂时容易丢失波场信息;能量比成像条件常用于估算反射系数,在非弹性界面处不稳定;互相关成像条件在各向同性逆时偏移中最常用,在实测资料的处理中取得了良好效果。为提高深部地层的成像效果或压制逆时偏移中的低波数干扰,又在此基础上提出了炮点波场归一化的互相关成像条件[69]和基于行波分离的互相关成像条件[70],前者可以提升深部地层的照明效果,后者需要依据传播方向进行波场分解,二者结合能够获得更好的成像效果。因此,常采用公式(1)所示的成像条件实现波场成像。

(1)

式中:x,y,z分别为三维直角坐标系的3个坐标;t为时间;tmax为记录长度;I为成像结果;s为炮点波场;r为接收点波场;Φ为波场传播方向;N为用于成像的波场传播方向个数。

公式(1)所示的成像条件本质上是一种成像思路或准则,没有限定具体的介质类型或方程形式,同样可用于解决qP波的逆时偏移成像问题。但前提是首先要获得各成像点在不同时刻的波场传播方向并依据该方向进行波场分解,因此如何准确地分离出沿各个方向传播的qP波是该成像条件的关键。郭旭等[71]通过求取VTI介质中qP波的坡印廷矢量指示波场传播方向并据此实现不同传播方向的波场分解,其思路同样可用于TTI介质,但坡印廷矢量的求取又要求对应的qP波方程中必须包含计算坡印廷矢量所需的应力分量和不同波型的质点震动速度分量。现有的许多qP波方程没有显式包含应力分量和质点震动速度分量,必须研究并采用其它技术求取qP波的传播方向,目前此方面的研究成果很少。

4.2 偏移噪声压制

qP波方程的逆时偏移噪声主要指由层间反射导致的低频噪声,这种低频噪声往往具有很强的能量,污染地层的成像结果(图4)。偏移噪声的本质是偏移算法本身的误差。

图4 TI介质逆时偏移中的偏移噪声

目前的偏移噪声压制思路有:①依据逆时偏移噪声的特点,研究并采用适当方法对已经产生的噪声进行压制处理,如拉普拉斯滤波法和带通滤波法[72]等;②依据偏移噪声的产生机理,通过改进波场延拓方法或成像条件避免产生噪声,如基于行波分离的互相关成像方法[70-72]等。前者属于先产生后压制的思路,本质上是一种信号处理技术,很难保证不伤害有效信号;后者注重从根源上消除其产生的“土壤”,一般依据炮、检波场的传播方向信息进行角度加权互相关成像,理论上具有更好的压制效果。

上述两种思路同样没有介质或方程的限制,均可用于TI介质qP波逆时偏移领域,杨富森等[73]和QIN[74]通过模型数据验证了这些思路对各向异性逆时偏移的适应性。

4.3 波场传播方向求取

求取qP波传播方向的必要性在于,波场分解或角度加权互相关成像条件的应用前提是要根据波的传播方向对炮点和接收点波场进行分类,然后只选择对最终成像有意义的波场参与互相关运算达到消除偏移噪声或提高照明均衡度的效果。目前一般以坡印廷矢量来指示波的传播方向,YOON等[75]和郭鹏等[76]给出的地震波坡印廷矢量E的计算公式为:

E=pv

(2)

式中:p为声压;v为质点振动速度矢量。

由于各向同性介质的一阶声波方程本身就包含了p和v这两个量,因此其坡印廷矢量的求取是非常方便的,但对于TI介质,二阶或高阶qP波方程很难直接得到p和v,此时无法在波场延拓过程中求得坡印廷矢量,只有将TI介质中的qP波方程写为一阶应力-速度方程组的形式才方便得到qP波的坡印廷矢量,进而获得波的传播方向信息并据此对炮点和接收点波场进行分类,因此,采用一阶应力-速度qP波方程进行逆时偏移有利于提高成像精度。

需要指出的是,地震波的坡印廷矢量是指单位时间内穿过与能量流动方向垂直单位截面的能量。当同一时刻在某成像点处存在多个具有不同传播方向的波时(在弹性分界面处这种现象一定存在),公式(2)求得的坡印廷矢量不代表某一特定的波的传播方向,而是该时刻所有波的传播方向的加权平均。由于逆时偏移中只需要部分波场参与成像,因此需要求出某一个或几个特定波的传播方向,坡印廷矢量无法实现,说明坡印廷矢量法不适用于多组波的情况。

如图5所示,当下行波I在t时刻传播至弹性分界面上的A点处时(假定入射角小于临界角),在该时刻会瞬间产生一个反射波R和一个透射波T,也就是说,A点在t时刻同时存在3个不同传播方向的波,而此时该点的坡印廷矢量P和上述3个波的传播方向都不相同,它其实是这3个波传播方向的加权平均,说明在多组波情况下,坡印廷矢量法求得的波传播方向存在较大误差。这一误差会传递给后续的波场分解或角度域权系数求取过程,导致最终成像精度的下降,且该误差在传递过程中的收敛性也难以确定,它对成像结果的影响目前也难以定量估算。

理论上,采用射线追踪类的方法可以消除这种误差,但用射线追踪法解决该问题的缺陷在于:①复杂构造条件下,TI介质的射线追踪技术难以解决多路径问题;②射线追踪法是一种“模型驱动”类算法,它的计算精度严重依赖弹性参数模型的精度,实际数据处理中给定的弹性参数模型存在较大误差,模型的误差会传递给射线追踪过程,最终降低波场成像精度,并且该误差在传递过程中的收敛性同样难以确定;③在波场延拓过程中必须同时进行射线追踪运算,增加了计算量与算法复杂度。这说明在TI介质逆时偏移领域,用射线追踪法解决波场传播方向求取问题具有不适应性,很难取代坡印廷矢量法。

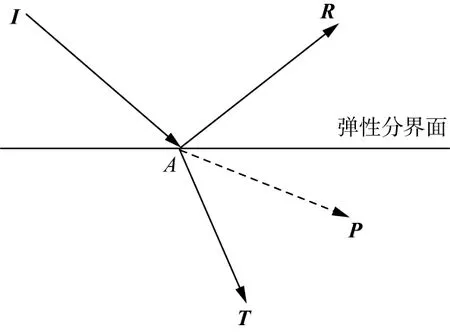
图5 多路径情况下的坡印廷矢量示意

尽管坡印廷矢量法存在上述缺陷,但目前仍然是地震波逆时偏移领域的主流算法。进一步提升波场分解精度的关键在于如何降低多组波情况下计算误差,目前业界在这方面没有可行的解决思路并缺乏深入的研究工作。

4.4 波场拉伸校正

逆时偏移的子波拉伸效应是指偏移后反射波在垂向上的子波延续长度和频率随地震波速度、地层倾角和反射角的变化而变化,造成共成像点道集(Common Imaging Gather,CIG)或角度域共成像点道集(Angle Domain Common Imaging Gather,ADCIG)中不同偏移距的地震道具有不同的频谱和分辨率的现象。图6为均匀TI介质中qP波方程逆时偏移脉冲响应分别用不同方式显示的结果(该脉冲响应的炮点位于地表2000m位置处),采用灰度显示时(图6a)看不出拉伸现象,但对该数据抽稀并采用波形显示时(图6b)则可以看到明显的拉伸现象,偏移距越大,波场在深度方向上的持续长度越大。说明逆时偏移的子波拉伸效应不是偏移算法本身的误差,而是一种视角效应,图6a的视角是波前的传播方向,是偏移过程的视角,图6b的视角是垂直向下方向,是偏移剖面的视角,说明偏移过程和偏移结果视角的不同是造成逆时偏移波场拉伸效应的原因。

目前解决逆时偏移子波拉伸问题的思路有3种:①先偏移后压缩[77-78],先用常规偏移方法得到拉伸后的偏移结果,再研发相关技术对已经拉伸的数据进行压缩;②先压缩后偏移[79-80],在偏移前先对地震炮记录进行时间上的压缩,然后再偏移成像;③在偏移过程中压缩[81-82],即在偏移过程中依据拉伸效应的产生机理采用适当方法避免产生拉伸。第一种思路的本质是试图恢复已经被破坏或损失的信息,很难达到理想效果,对于第二种思路,由于在偏移前压缩地震记录会破坏地震数据原来的动力学特征,而逆时偏移本身并不具备恢复这些动力学信息的能力,必然以降低偏移结果的保真性为代价,同时这种思路在操作上也存在巨大困难;第三种思路具有理论基础的先天优势,在理论上能够减弱子波拉伸对偏移结果的影响。

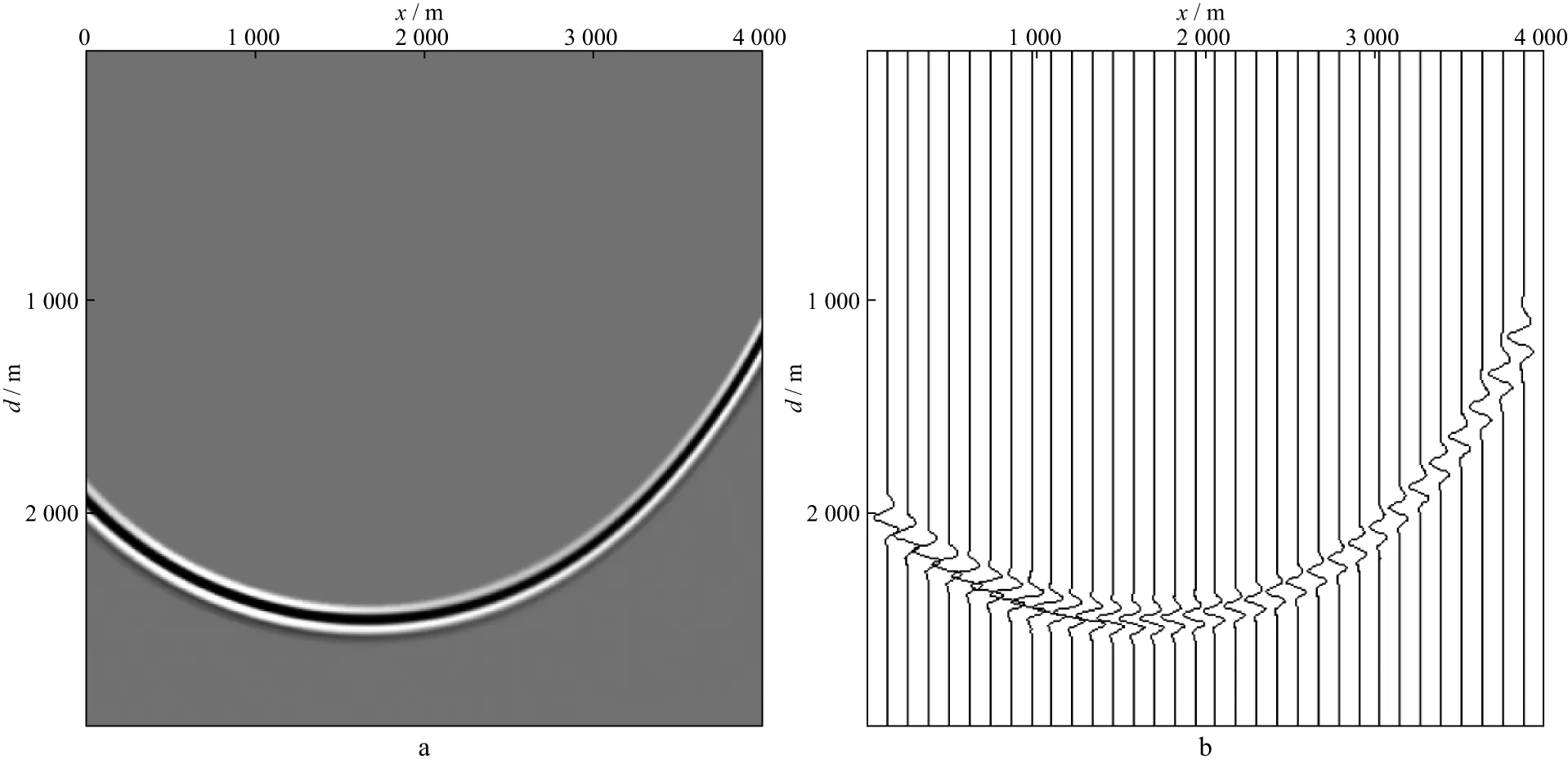
图6 qP波方程逆时偏移的脉冲响应

ZHU等[81]依据逆时偏移子波拉伸的产生机理给出了各向同性声波方程逆时偏移的子波拉伸校正方法,算法的本质是在偏移过程中进行视角转换,只要地震波入射角和反射角求取准确,这种算法就能消除逆时偏移中的波场拉伸现象。杨佳佳等[82]改进了反射角和入射角的计算方法,将该算法扩展到弹性波领域,并在模型数据和实测资料的处理中均取得了效果。

ZHU等[81]和杨佳佳等[82]的工作对于qP波逆时偏移的波场拉伸校正虽然具有很强的借鉴意义,但不能完全照搬,qP波逆时偏移中波场拉伸校正的特殊性表现在:①算法只适用于激发时间成像条件,而激发时间成像条件对深部地层的成像能力不足;②地震波入射角和反射角的求取需要已知波的传播方向信息,在各向同性声波领域,可以方便地利用坡印廷矢量来指示波的传播方向,但目前的许多qP波方程不能提供求取坡印廷矢量必需的振动速度和应力信息,导致坡印廷矢量求取失败。因此,针对具体qP波方程本身的特点,研发适用于各向异性qP波方程的逆时偏移波场拉伸校正技术极为必要,但截止目前,还未见到该方程的研究成果与文献报道。

5 存在的主要问题及未来发展展望

综上所述,本文认为在TI介质中的qP波逆时偏移领域尚存在以下问题需要解决:

1) 对qP波方程的动力学精度缺乏深入研究。由于qP波方程是弹性波方程的近似,其近似效果的评价应该同时包括运动学和动力学精度两个方面,而目前的研究工作均停留在方程运动学精度的分析层面,对方程动力学精度的研究尚未展开。运动学特征的近似程度决定了构造成像的准确度,动力学特征的近似程度决定了偏移结果中的能量信息能否用于反演或解释岩性,如果对方程动力学精度的认识不足,则会导致对偏移结果中地震波能量信息的利用率不足或应用失败。

2) 对qP波方程逆时偏移中的随机边界技术缺乏深入研究。因为随机边界技术的炮点波场逆时重构是提升逆时偏移效率的关键,在各向异性情况下,由于qP波方程包含多个各向异性参数,这些参数共同决定求解算法的稳定性,所以随机边界中各向异性参数的设置是相互关联的。如果用各向同性领域的随机值设置方法分别独立设置边界处的各向异性参数,会导致延拓或重构过程出现不稳定现象。因此,各向同性逆时偏移中的随机边界技术不能直接用于解决各向异性逆时偏移问题,而应当研发具有完善理论的随机边界各向异性参数赋值方法。

3) 在qP波方程逆时偏移中波场传播方向的求取方面需要展开更深入研究。不同时刻波场传播方向信息的准确求取是波场成像、偏移噪声压制以及波场拉伸校正的关键,实际求解中可以用坡印廷矢量指示波的传播方向,但坡印廷矢量的求取要求首先已知各成像点在不同时刻的应力矢量和质点振动速度矢量,对qP波方程提出了以下要求:方程中最好能包含应力矢量与振动速度矢量;或便于求解不同时刻各质点的应力矢量与振动速度矢量;最好是一阶方程且便于快速稳定求解。同时,现有的坡印廷矢量技术还存在当同一点在同一时刻有不同传播方程的多个波时,坡印廷矢量只能得到一个混合波场传播方向的缺点。因此,必须深入研究更准确的波场传播方向求取技术。

6 结束语

本文初步总结了TI介质中qP波逆时偏移技术的研究现状,分析了现有技术的实现思路和存在的主要问题,在此基础上给出了进一步研究建议。

各向异性理论的qP波逆时偏移是一个庞大的技术体系,受文章篇幅和作者水平的限制,本文无法就这一技术体系中每个细节的研究现状与存在的问题展开讨论,只能讨论该体系中部分重点环节,即使在这些重点讨论的环节中也可能因为作者水平问题遗漏其中的重要方法和文献。

本文在总结过程中没有考虑各向异性建模问题,而这一问题又是逆时偏移技术应用前必须解决的,各向异性建模中的相关技术和难点问题需要另文讨论。

地震各向异性资料的成像处理是一个系统工程,不能只靠逆时偏移一个环节解决问题,还应当包括去噪、静校正、反褶积和弹性参数建模等诸多环节,只有解决了各个环节的问题才有可能最终解决各向异性地层的地震波成像问题。