勘探地震中的六分量观测

王 赟,孙丽霞,李栋青,陈 畅,邱新明

(中国地质大学(北京)地球物理与信息技术学院“多波多分量”研究组,北京100083)

1 六分量地震概况

空间中任意一点的运动状态有六个自由度(图1),即需要完整地刻画3个平动分量和3个旋转分量[1-2]。由震动引起的旋转是地震学研究的重要方向之一[3-4]。伴随着旋转地震仪的研发日益成熟,旋转观测在天然地震、地震工程、建筑工程和火山监测等不同领域都获得了广泛的应用[5]。为推动国际间对地震旋转运动的关注和加强合作,美国地质调查局的LEE联合多位地震学家于2006年成立了International Working Group on Rotational Seismology(IWGoRS)合作小组,该小组每三年召开一次旋转运动学术讨论会[6],截止目前,旋转运动的观测研究主要局限于美国、欧盟和日本等一些发达国家及中国台湾地区,并以天然地震和地震建筑工程领域为主,鲜有勘探地震领域的实际应用。

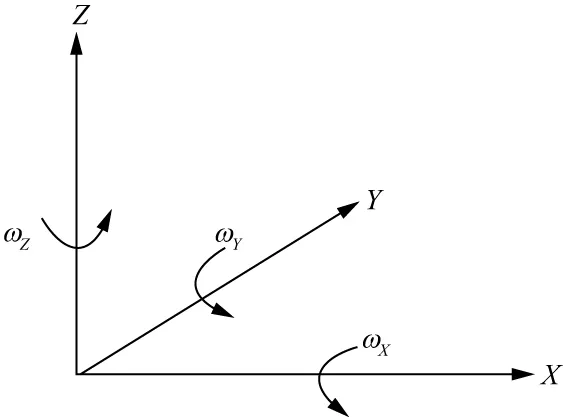
图1 三维正交笛卡尔坐标系统中的旋转运动示意[2]

除目前的平动3分量地震观测外,Stanford大学近十年一直倡导在勘探地震中进行3个旋转分量的数据采集,并进行旋转分量观测应用于勘探地震的可行性研究[7]。BARAK等[8-9]在常规海底四分量地震观测(包括压力和笛卡尔坐标系下3个方向的线性位移振动)的基础上,强调增加3个分量记录质点旋转运动的重要性,通过简单的水下散射体波场模拟,说明了7分量记录的地震波场对于有效描述不同类型波的振动轨迹,恢复波场的空间矢量特征具有重要意义;并从去噪的角度阐释了利用7分量记录去除面波和折射波的方法以及技术优势。BARAK等[10]还给出了利用奇异值分解识别并分离旋转分量中面波和体波的方法。PHAM等[11]研究了均匀各向异性弹性介质中平面波的传播,发现了各向异性对旋转分量波场的影响。理论上,在各向同性介质中纵波不能产生旋转运动,而各向异性会引发旋转运动的产生。SUN等[12]在旋转运动产生机理研究的基础上,进一步讨论了体波与面波在旋转分量上的不同投影及其波场频散特征,为利用不同分量上的基阶和高阶频散曲线精确反演面波相速度提供了理论依据。

2019年,第5届IWGoRS会议在中国台湾地区召开。会议围绕旋转地震观测、数据分析、行星和火山的观测、结构成像、地震波理论研究、旋转观测仪器以及阵列观测共7个方面展开,涉及旋转地震学在工程、油气、海洋、火山、行星和建筑等方面的诸多应用。SCHMELZBACH[13]从旋转分量观测数据发掘利用的角度论述了六分量观测记录到的旋转运动信息,以及可以换算获得的波场梯度在勘探地震中可能的多种应用,提出利用稀疏六分量观测替代密集排列观测就可以实现地下介质结构的属性反演,大幅度降低采集成本;从理论上论证了利用六分量的极化分析代替平动三分量可以实现精度更高的不同类型波场识别和分离,包括面波的分离和提取(或压制)、上下行波分离和弹性波解耦;针对海底四分量观测,尝试增加旋转三分量观测以实现水声的梯度场观测,认为有望突破Shannon-Nyquist采样定律实现稀疏波场重建,为六分量地震观测在勘探领域的应用预示了美好的前景。

理论上,旋转分量观测在勘探地震中可衍生出许多应用,主要包括识别体波和面波、识别和分离P波与S波波场、波场重建、去面波(极化滤波)、微震震源定位,以及利用波场延拓方法实现地震偏移成像,利用旋转分量进行地震反演、监测裂缝损伤,基于AVO分析研究地下介质属性、速度层析成像等,对此,LI等[14]曾对此进行了综述。但限于旋转地震仪价格昂贵,已有的勘探地震应用多属于理论推测、科学实验或小规模测试,距离勘探地震的大规模应用尚有差距。为此,本文从推动六分量地震观测应用于油气勘探地震领域的角度,介绍了两种在没有旋转运动观测的条件下,通过勘探地震高密度平动三分量地震观测换算旋转分量的方法,并通过六分量地震波场模拟以及不同类型面波在六分量地震记录上特征的讨论,介绍六分量地震观测可能给勘探地震带来的新视角和技术变革。

2 地震旋转分量波场特征

在经典线性弹性小变形假设下,根据弹性动力学理论[15],均匀各向同性弹性介质中的波动方程可以写为一阶速度-应力方程形式,即

(1)

式中:σij表示应力,i,j=1,2,3,分别表示三维正交笛卡尔坐标系中的X,Y,Z3个方向,ρ表示密度,λ和μ为拉梅系数,vX,vY,vZ分别表示X,Y,Z3个方向的质点振动速度分量。

对公式(1)采用交错网格有限差分方法,时间采用2阶,空间采用12阶,顶边界采用自由地表条件,左、右及底边界采用分裂形式的完全匹配层吸收边界条件消除边界反射,可以模拟任意各向同性弹性介质情况下的地震波传播速度场[16-17]。根据旋转张量的定义,以旋转速率表示的旋转张量为:

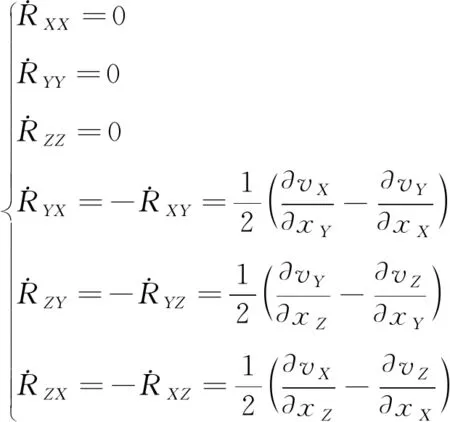
(2)

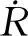
根据公式(2)可以输出三分量旋转速率,与三分量平动速度共同组成地震波的六分量速度场。例如表1所示三维的两层介质模型,模型尺度为100×100×130m,检波器分布于自由地表,间距1m,炮点位于地下5m;采用主频为50Hz的Ricker子波分别加载在速度、正应力和剪应力上,可分别模拟3种震源类型(集中力源、爆炸源、剪切源)激发情况下的自由地表六分量记录,如图2至图7所示。

表1 三维均匀各向同性弹性介质模型参数

图2 爆炸源产生的六分量地震记录(平动分量)

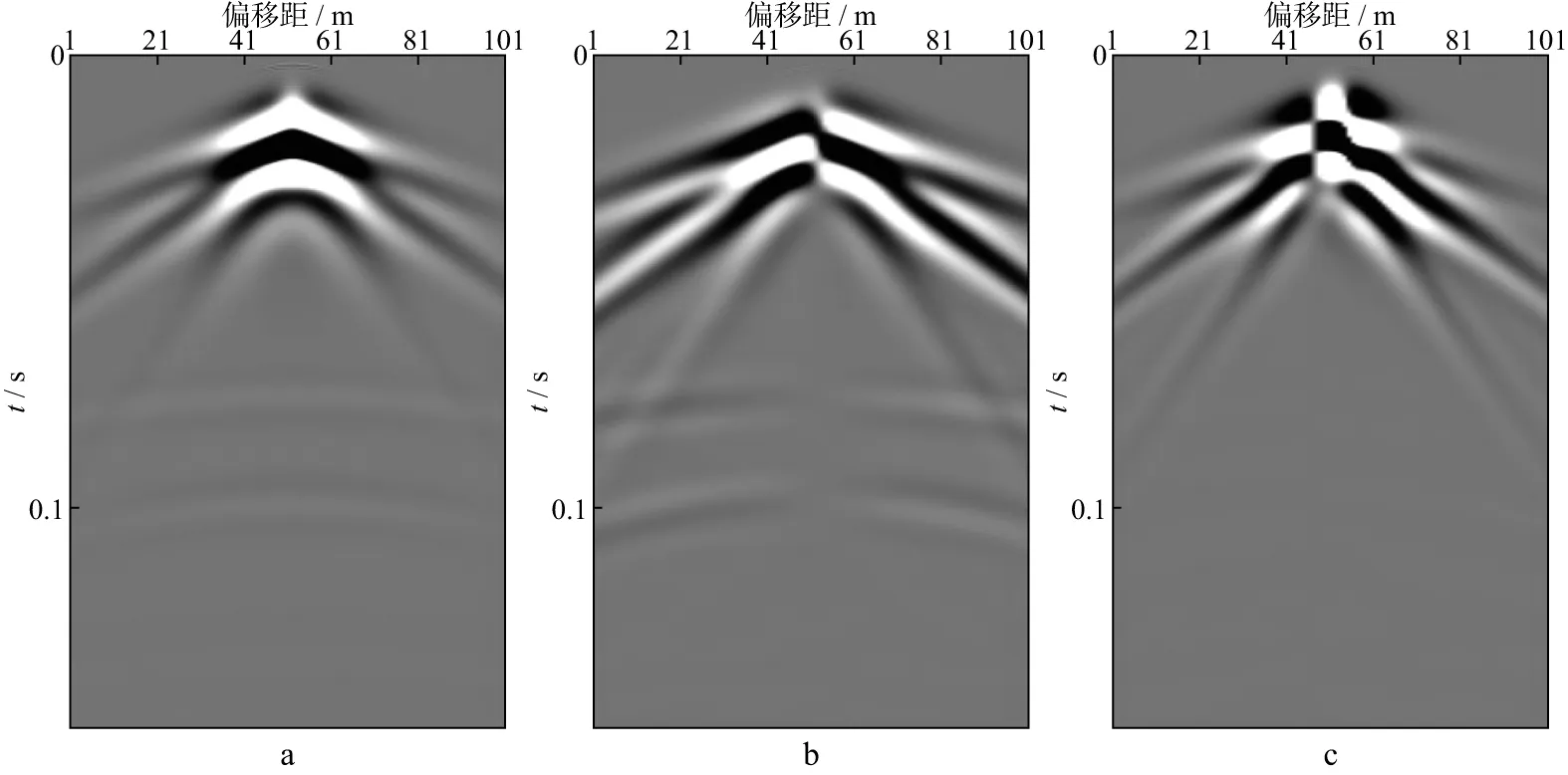
图3 爆炸源产生的六分量地震记录(旋转分量)

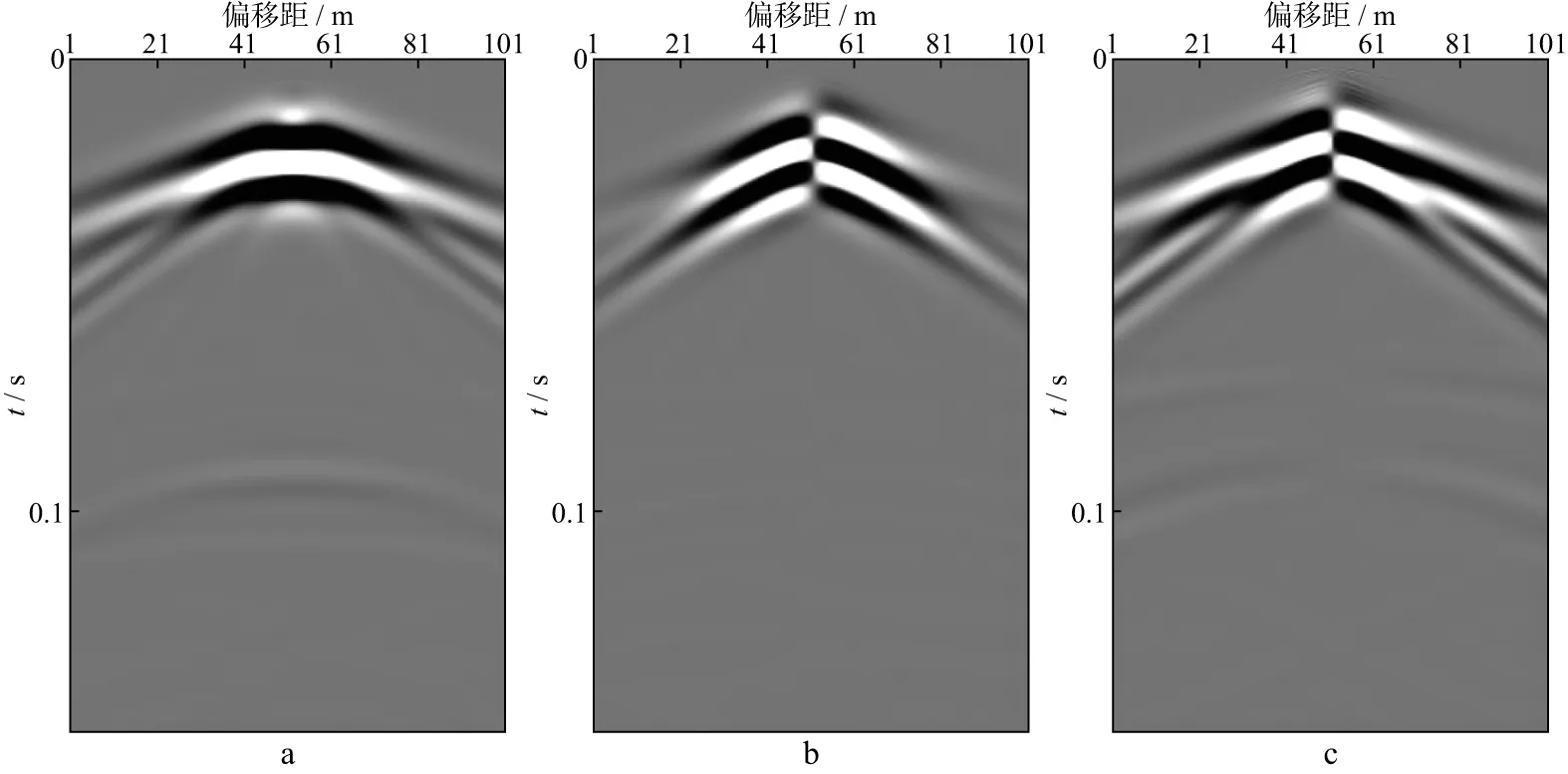
图4 径向集中力源产生的六分量地震记录(平动分量)

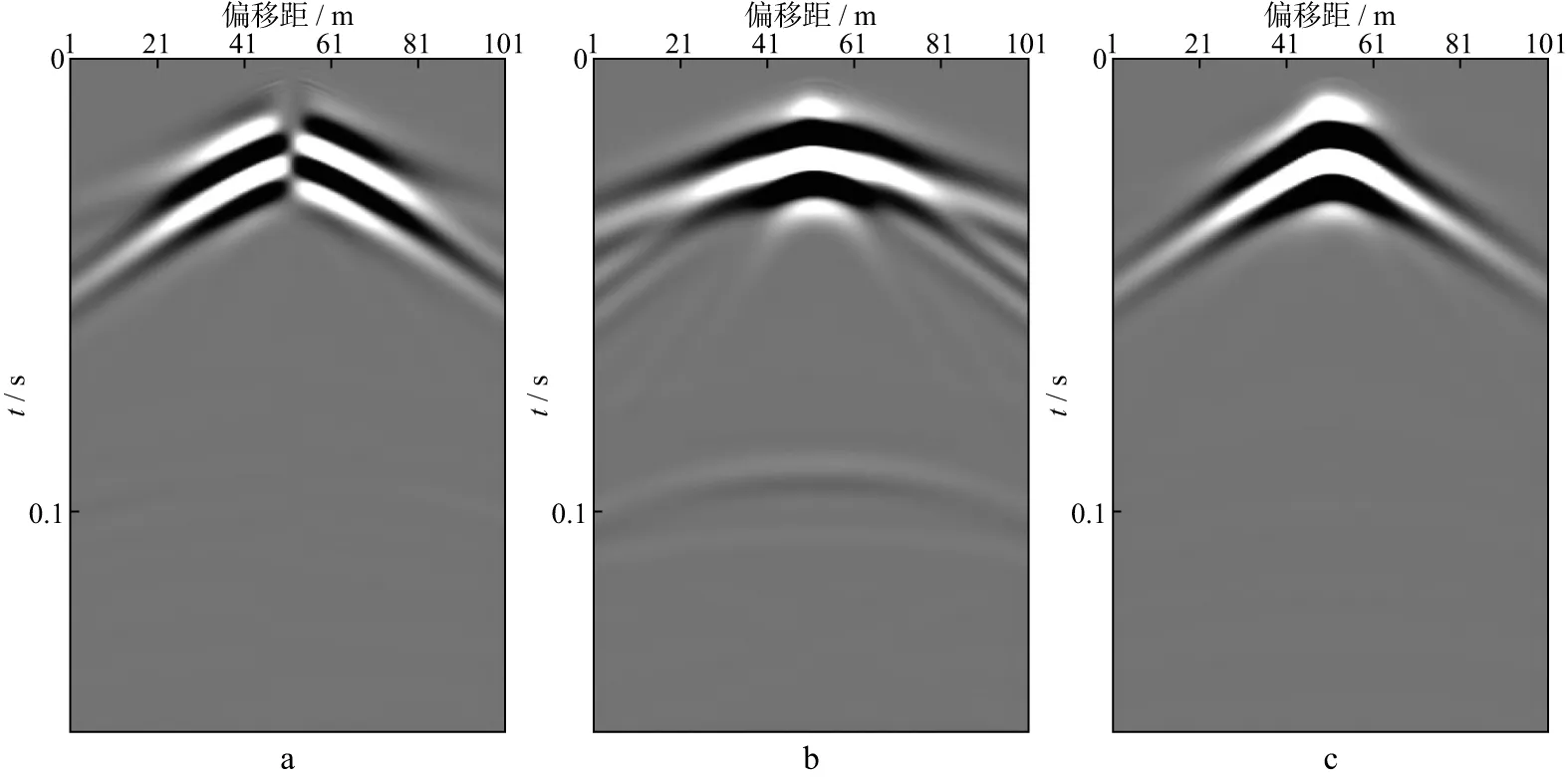
图5 径向集中力源产生的六分量地震记录(旋转分量)

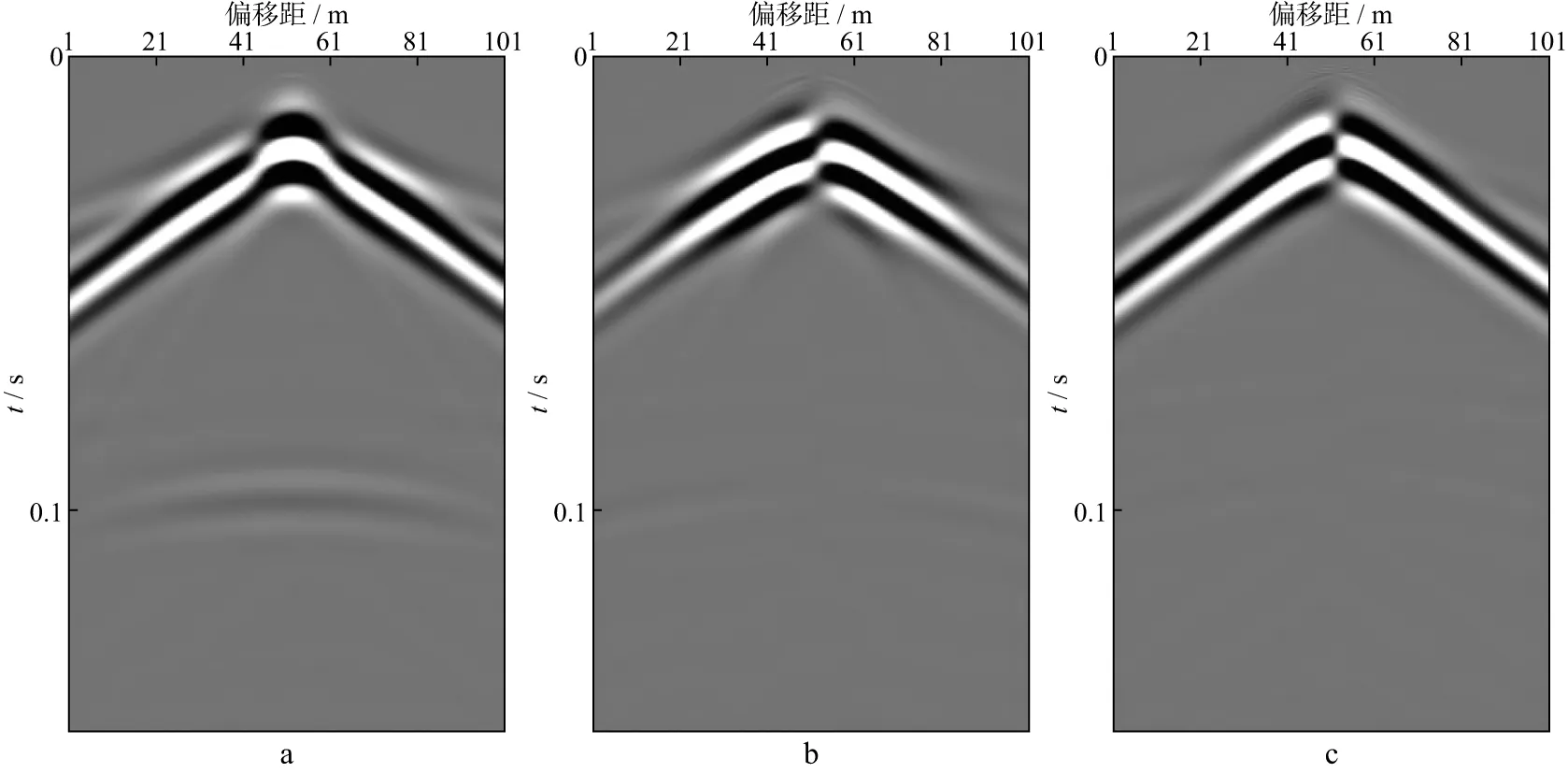
图6 剪切源产生的地震记录(平动分量)

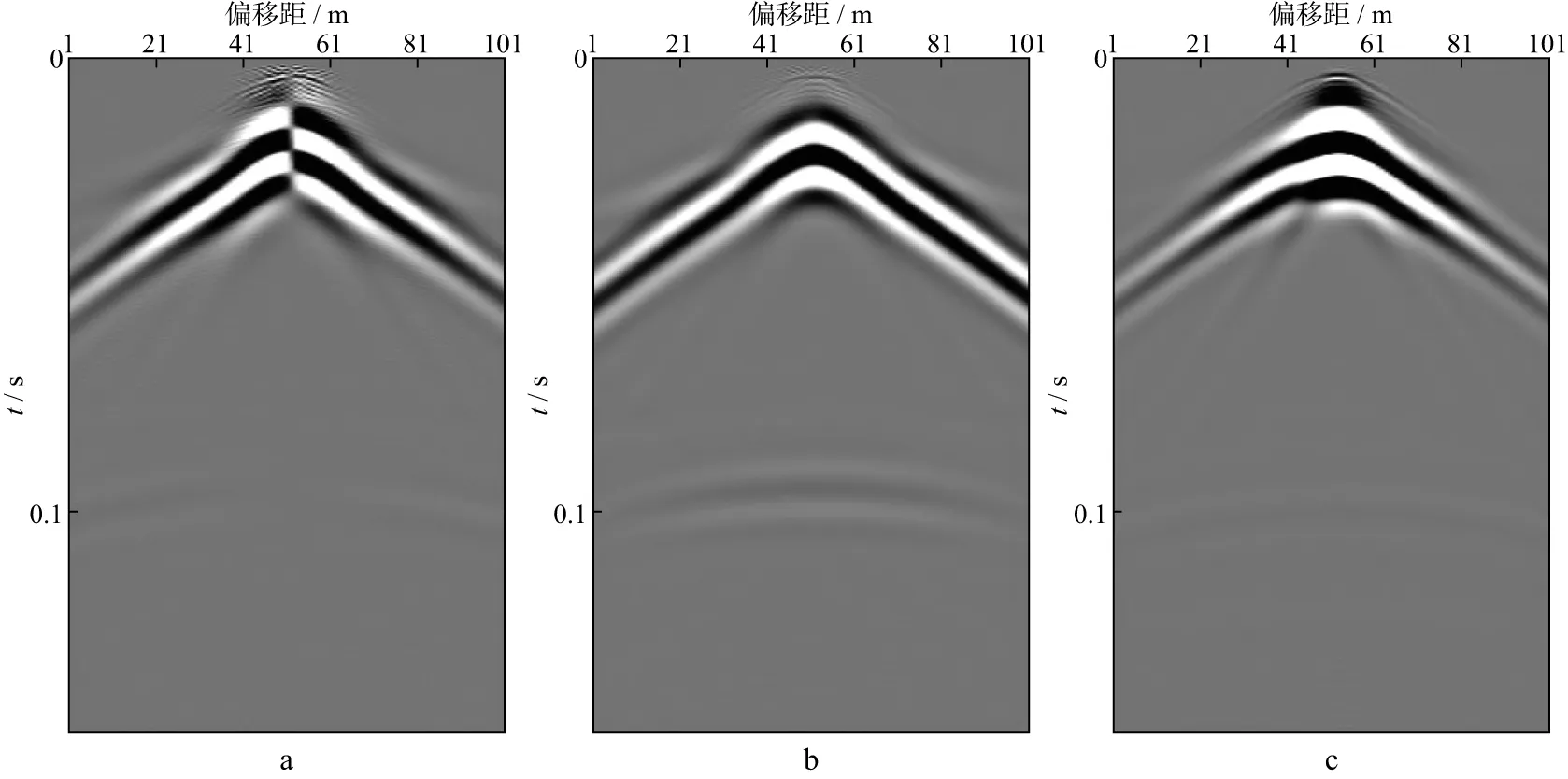
图7 剪切源产生的地震记录(旋转分量)

由图可见,不同源情况下六分量记录中分别存在直达波、面波、反射P波和PS波、S波。对比六分量记录发现:①面波能量在所有分量上均存在,且存在频散;②平动Z分量上的P波与S波能量强;③爆炸源产生的反射波能量最强;④在径向集中力源(本例中设定力源方向为inline方向,即X方向)和剪切源情况下,Y、Z和RX分量在震源两侧初至波和反射波呈反极性特征;而爆炸源的初至波和反射波的反极性出现在X和RY分量上[18]。

上述模拟结果说明,六分量地震记录有利于了解地下介质振动状态,在不同领域应用可能会产生不同的效果。

3 间接换算法

目前,勘探地震中鲜有六分量地震的观测。由于旋转运动的记录对于地震仪器硬件要求较高,旋转地震仪价格一直居高不下,且现有的旋转观测仪器频带宽度、动态范围和稳定性等一直难以满足勘探地震大量使用检波器的要求[4],因此,在线性弹性动力学理论框架下,针对目前勘探地震领域三分量平动地震宽方位、高密度采集的特点,采用差分法[19]和行波法[20]将观测的平动三分量地震数据换算成旋转分量是一种可行的选择,即在只有平动三分量地震观测的情况下,通过某种近似计算获得旋转分量[21]。

3.1 差分法

差分法是随着天然地震领域出现密集台阵观测而产生的利用观测平动分量近似计算旋转分量的间接方法[22-24]。根据旋转张量定义,在高密度观测条件下,当满足:①相邻观测点的距离远小于地震波波长,②地震引起的地下介质振动满足线性小变形弹性理论假设时,3个旋转分量可以通过平动波场数值差分的形式求解。其中:两个水平旋转分量RX和RY使用两个相邻物理点的平动分量即可获得,一般称为两点差分法;而RZ分量需要3个正交相邻点的平动记录,因此,称为三点差分法。在勘探地震平动三分量三维观测条件下,可以进一步使用精度更高的四点、五点差分法[25]实现旋转分量的换算。

以中国台湾地区中央研究院地球科学研究所在兰溪河谷采集的爆炸震源六分量地震观测数据[26]为例,进行差分法换算旋转分量,并将计算出的旋转分量与实测结果对比,本次旋转分量观测使用的是EENTEC公司研制的R-1旋转地震仪,其优势频率为43Hz。本文只截取观测数据中500ms的波形,分别使用两点(单边)差分格式和四点(中心)差分格式[27],将观测的平动三分量地震记录差分换算成RX分量(图8),图9是对应的振幅谱对比。由图可见,换算的旋转分量与实际观测记录相似性较好;两点和四点差分法换算的旋转分量与实际观测波形的相关性分别达到0.58和0.72,振幅谱的相关性更是达到了0.86和0.88。需要注意的是,为便于对比,分别对实际观测和换算的旋转分量进行了归一化处理,因此,此图显示的是相对振幅和频谱的关系。

3.2 行波法

行波法是NEWMARK[28]提出的,该方法求取旋转分量不需要密集观测,但它假定地球介质是均匀弹性介质,平面波以一定速度沿一定方向传播,利用相关分析求出准确的视波速[29]后,再利用公式(3)进行自由表面上的平动和旋转分量间换算:

(3)

式中:u1,u2,u3分别表示沿X,Y,Z轴的平移运动;RX(t),RY(t)和RZ(t)是旋转分量;Ca为视波速;φ为波传播方向与X轴的夹角。

利用前述的有限差分方法,在弹性小变形假设下,针对一个水平层状各向同性均匀介质模型,模拟六分量地震记录,对比由平动分量经行波法计算得到的旋转分量与模型理论模拟值之间的差异,归一化后的旋转分量如图10所示。可以看出,直达波的行波法换算旋转分量与理论模拟旋转分量在初至时间、直达波波峰、波谷位置对应时间上具有良好的一致性,在相位上也与模拟值一致[20]。

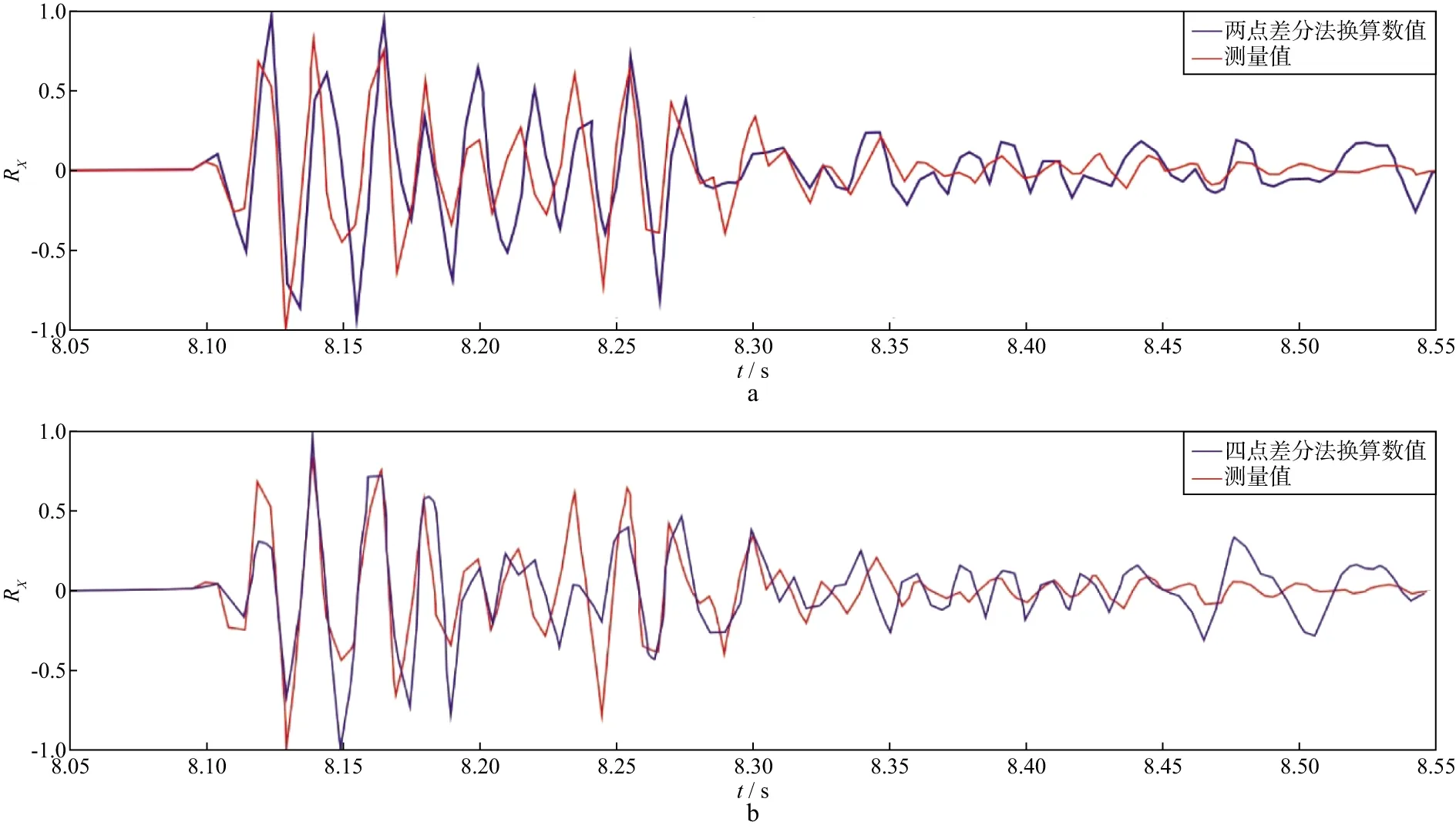
图8 两点(a)和四点(b)差分法计算的RX分量时间域波形对比

同时,需要注意的是,采用行波法求解旋转分量时,包含了波速为常数和沿传播路径上任意两点的波完全相关这两个假设,而地震波传播时因介质的不均匀性以及不同的波型以不同的速度传播,导致波速的改变,使得这两个假设过于理想化,行波法的结果存在误差[30]。

采用实际观测数据进行行波法换算,发现利用平动分量计算旋转分量的幅值比实测值小;对比两点差分法的结果(图11),证明了在处理实际数据的过程中,针对直达波,行波法比依赖密集台阵地震记录的两点差分法精度更高。

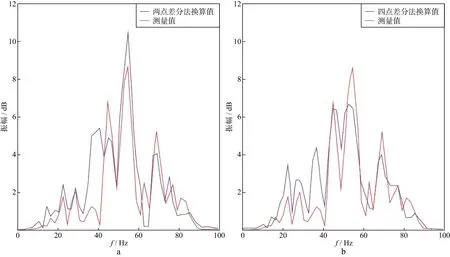
图9 两点(a)和四点(b)差分法计算结果振幅谱对比

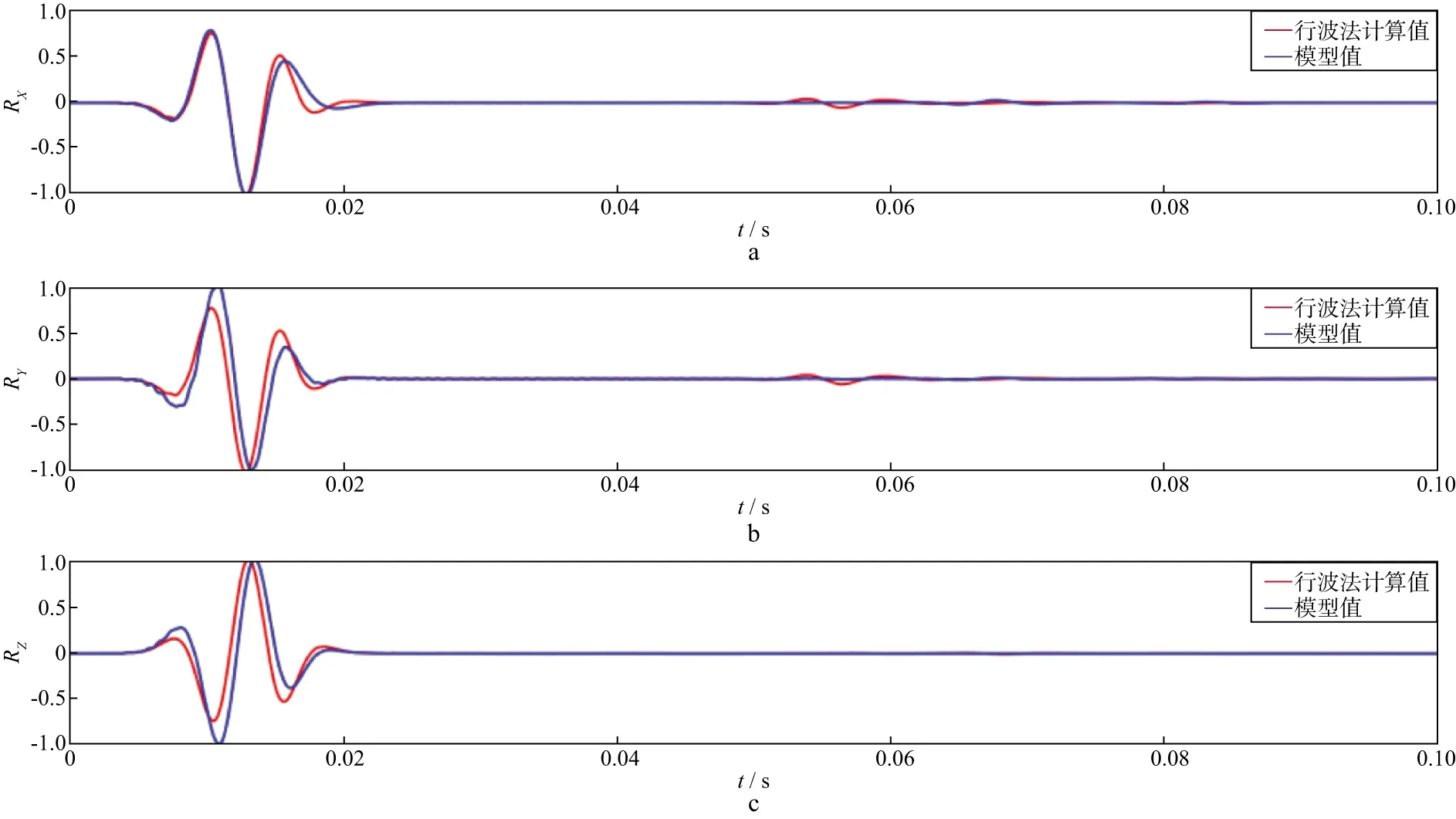
图10 归一化后模拟数据中第30道旋转加速度分量对比

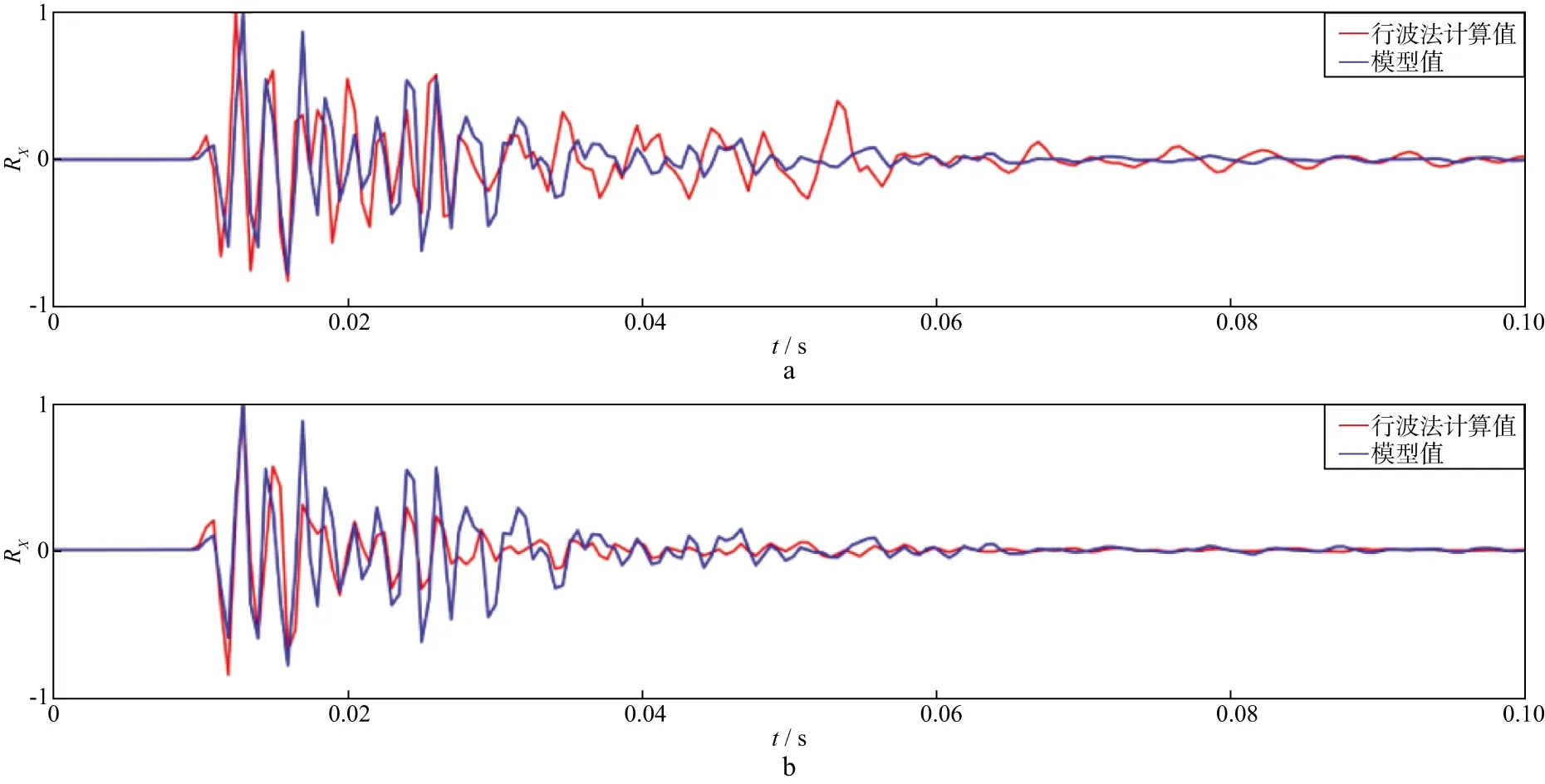
图11 N06台站旋转加速度RX分量对比

4 面波的六分量波场特征

无论在天然地震领域还是勘探地震和工程地震领域,面波都广泛应用于浅层横波速度的层析和结构调查[31-32],但现有应用大多是利用Z分量数据或平动三分量数据[33-35]。利用地震旋转分量研究面波,是六分量地震的重要应用方向之一。为此,我们设计了浅层地质模型(表2),采用前文介绍的有限差分方法进行面波模拟分析。模拟中,空间间距设置为0.1m,时间采样间隔为0.1ms。图12为垂向集中力源激发产生的六分量波场在inline线最小偏移距检波点的波场记录,明显看出,X,Z和RY分量的波场能量较强。图13为对应的频率-速度(f-v)谱,图中白色点线是Rayleigh波的理论频散曲线。由图可见:①RY和Z分量上的频散能谱相近,均不同于X分量;②这些频散能量团的连线与Rayleigh波的理论频散曲线一致,因此,主要反映Rayleigh波信息。

图14为横向集中力源的六分量模拟结果,力源方向为crossline(Y)方向,显然Y,RX和RZ分量上存在明显的波场能量。对应的f-v谱如图15所示,频散能谱上的能量团对应了Love波的理论频散曲线(图中白色点线),且RZ分量上显示更清晰;而RX分量的频散能谱发散,可能是Rayleigh波干扰。

从上述两例的模拟分析可以看出,旋转分量有助于我们认识震源类型和近地表模型。当垂向集中力源激发时,主要产生Rayleigh波,波场能量主要记录在X,Z和RY分量上;而横向集中力源主要激发产生Love波,其能量主要记录在两个水平方向平动分量和RZ分量上。旋转分量记录波场信息具有不同于平动分量的频散特征,从而可以说明旋转分量观测对于近地表横波速度的研究意义重大。

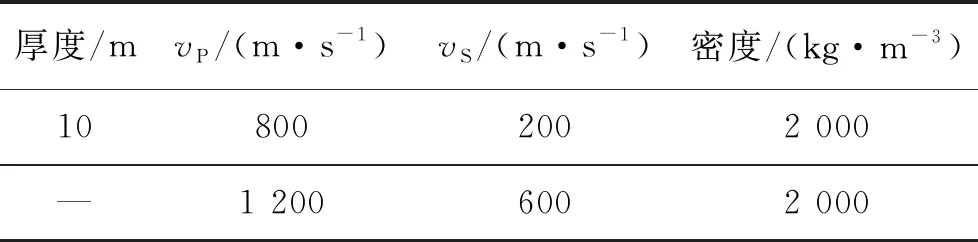
表2 浅层地质模型参数

从该简单浅层模型模拟记录及其波场频散特征分析可以看出,不同类型的震源激发不同类型的面波,从而在不同分量的记录上呈现不同或相似的特征,对于研究产生面波的源的性质,以及利用不同分量的面波频散曲线提高浅层横波速度结构层析反演的精度是值得深入探索的方向。

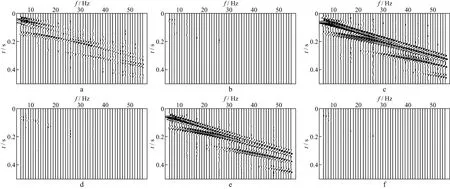
图12 垂向集中力源激发产生的六分量地震波场

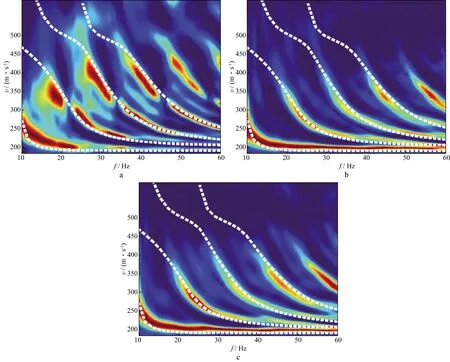
图13 X(a),Z(b)和RY(c)分量对应的f-v谱

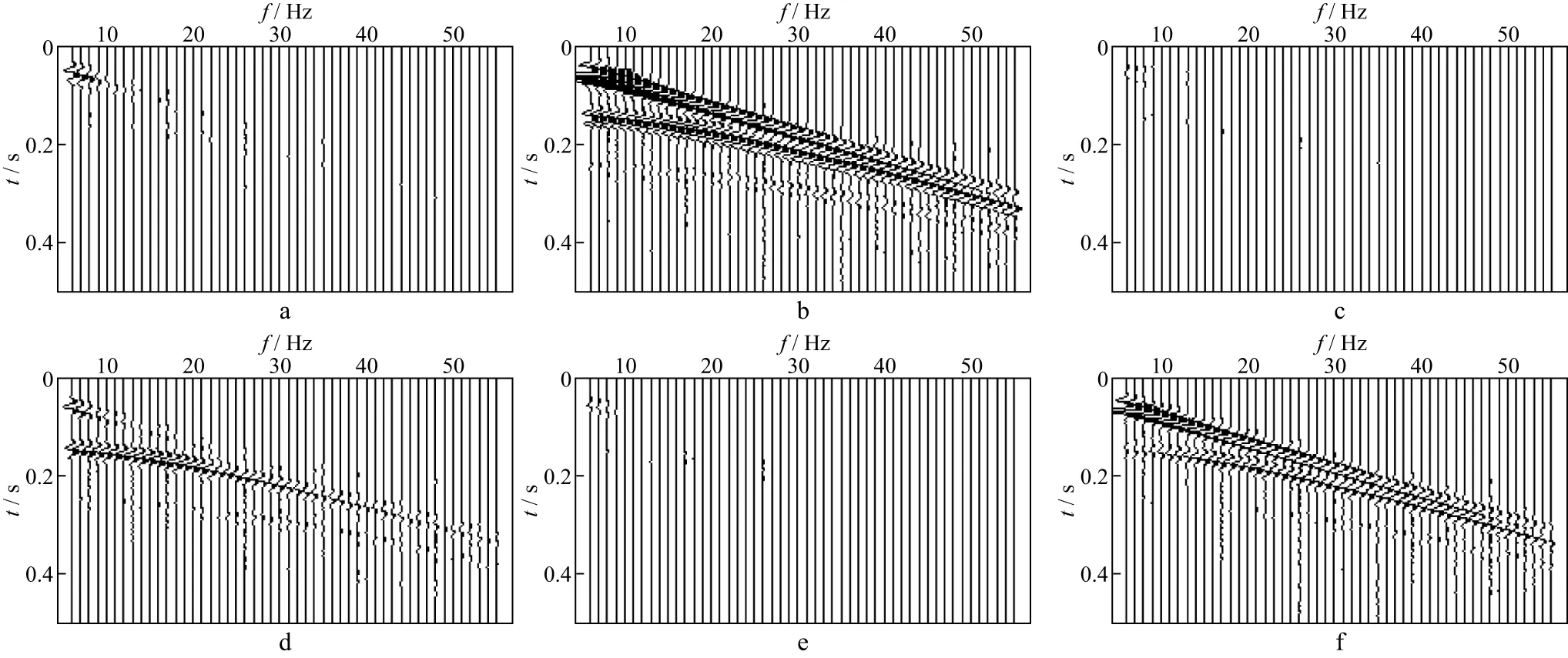
图14 横向(crossline方向)集中力源激发产生的六分量地震波场

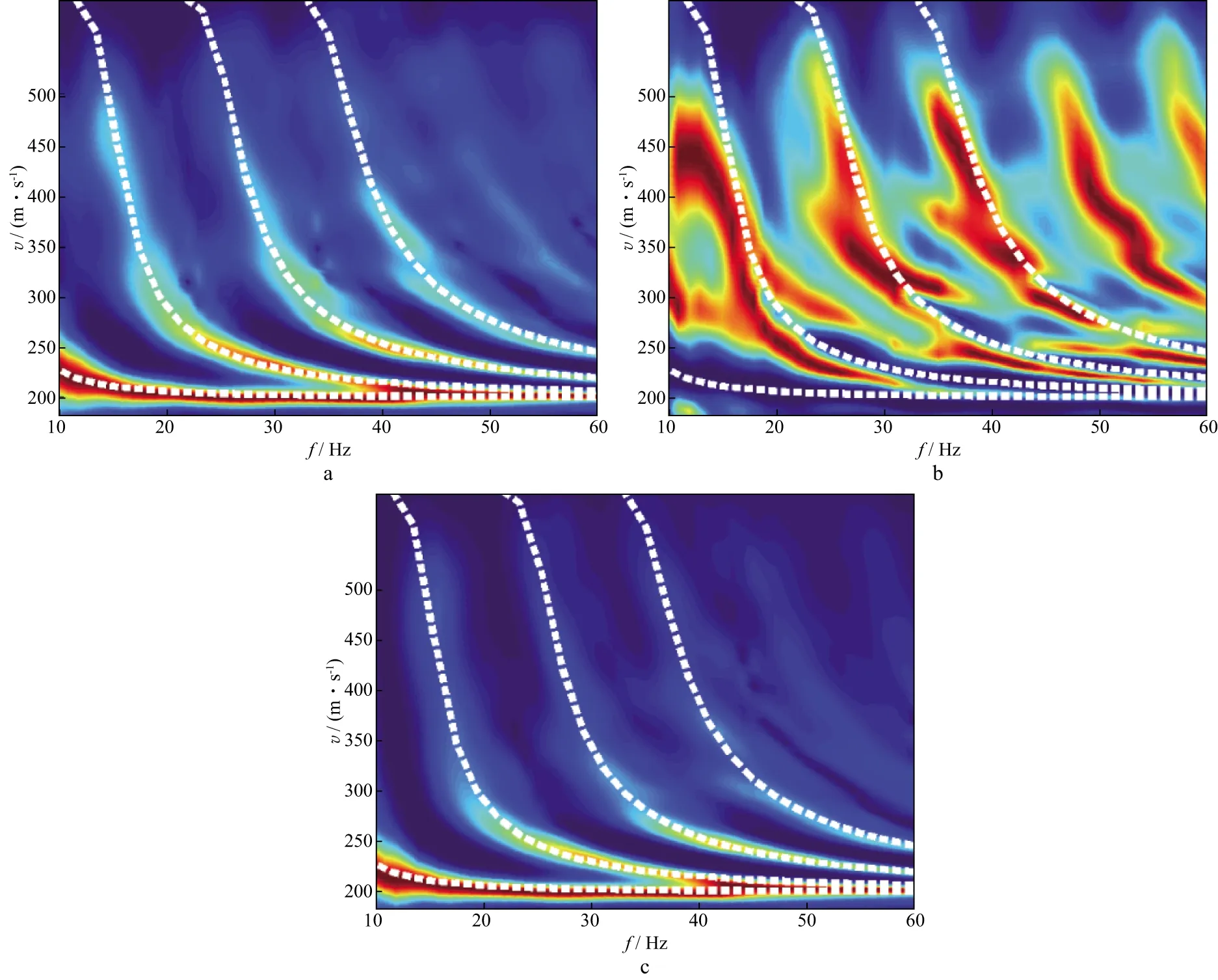
图15 Y(a),RX(b)和RZ(c)分量对应的f-v谱

5 总结与展望

根据前文所述的不同震源类型与波型的六分量地震波场特征可知,旋转分量观测对于地震波型识别和波场分离等诸多领域具有深入研究价值,应当引起勘探地震界的重视。六分量观测对于勘探地震的意义,SCHMELZBACH等[2]给出了相对完整的方向指引。综合地震学领域讨论的在勘探地震中采用六分量观测的意义,主要存在以下几个方面值得深入讨论和未来进一步攻关研究。

1) 从应变和旋转张量的定义可知,在勘探地震中,不论是速度检波器还是加速度检波器,当平动三分量采用十字型小面元组合方式观测,或具有旋转分量观测时,该观测物理点或面元处垂向梯度场可以定量换算,使得该点的应变和旋转张量具有完备的观测值,进而使得该点附近的波场属性,包括相速度、传播方向和波型等信息的提取成为可能。针对此设想,SCHMELZBACH等[2]和SOLLBERGER等[36]利用理论分析和一个小型观测试验给出了详细的勘探地震设计和分离纵波、横波以及反演浅层速度结构的实现方法,并针对不同检波器间可能存在的扰动压制问题给出了较好的解决方案。SCHMELZBACH等[2]还尝试利用VSP六分量观测分离上下行波和P波与S波。

2) 由于不同的波型在六分量上具有不同的波场特征,综合利用初至、波形、振幅、相位、偏振和频散等信息,可以通过单个物理点的六分量观测实现弹性波的波场识别和分离,而在常规三分量平动观测中,一般需要一个排列的密集观测才能达到此目标。

3) 从本文的数值模拟和孙丽霞[16]、PHAM等[11]的模拟可以发现,旋转分量与横波密切相关。因此,对于横波成像或转换横波成像,旋转分量发挥着重要的作用。尤其在密集台阵旋转观测换算梯度场或直接观测纵向梯度场条件下,利用不同深度的波场信息提高成像精度,实现P波和S波波场的有效分离是可行的。目前勘探地震中通过高密度观测实现的波场重建,在梯度波场已知的条件下更容易实现,且不需要大量的密集物理观测点。而介质的各向异性所引发的旋转运动出现,使得利用旋转观测反演介质的各向异性参数增加了可靠的约束条件,如PHAM等[11]数模分析显示,当P波出现在旋转分量上时,只有在介质各向异性的条件下才能存在。前文提到的面波模拟例子看出,浅层工程或勘探地震的面波在旋转分量上具有足够强的能量投影,综合利用Rayleigh波和Love波,有望实现高于传统方法精度的浅层横波速度结构精细层析。

4) 由于微震与天然地震在发震和传播、观测等诸多方面的相似性和可类比性,利用天然地震震源反演的方法技术实现压裂微地震的动态监测和高精度定位是最现实、可行的研究方向之一。尤其在勘探地震和天然地震融合发展的当下,利用六分量地震观测实现微地震的高精度预测是非常可行的。实际上,在勘探地震中,若能实现近震源的旋转观测,对于定量评估震源的性质和地震波的传播也十分有意义。尤其在目前多方向可控震源技术迅速发展和推广应用的趋势下,旋转分量的观测将十分有利于波场的分离和叠加。

5) 若能在海底观测中实现六分量或七分量的地震记录,不利用密集排列和初至波走时信息,就可以实现不同类型波的初至识别以及各波型的分离、上下行波的分离,并实现OBS的方位和倾斜校正,进而通过地震旋转观测,建立海底电磁和地震的关联,实现震电的联合反演。关于这方面内容,美国地质调查局曾给出一个观测实例[37],值得领域内进一步深入探索。

致谢:本文所使用的中国台湾地区旋转观测数据来自中国台湾地区中央研究院地球科学研究所的黄柏寿研究员,他所领导的旋转运动研究团队给我们的研究提供了诸多帮助;特别感谢林正洪博士在数据使用上的协助。