多分量面波研究进展

邱新明,王 赟,韦永祥,钱忠平,范秦军,钱荣毅

(1.中国地质大学(北京)地球物理与信息技术学院,北京100083;2.福建省地震局,福建福州350003;3.中国石油集团东方地球物理公司物探技术研究中心,河北涿州072750;4.黄河勘测规划设计研究院有限公司,河南郑州450003)

近地表传播的面波包括瑞利波和勒夫波,其中瑞利波由P波与SV波相互干涉形成,勒夫波由SH波的多次反射、折射叠加形成[1-2]。面波因具有横向传播衰减小、信噪比高及频散等特点,故广泛应用于地球壳幔结构成像、岩土工程勘查、油气勘探等领域[3-5]。在油气勘探领域,近地表条件影响着地震数据的品质。复杂的近地表条件会造成严重的静校正问题[4],进而影响地震数据的品质。面波勘探是解决近地表结构问题的重要勘探方法之一,高频(>1Hz)面波分析方法主要利用面波相速度频散特性揭示地下介质的横波速度结构[6]。研究表明,层状介质中存在多个模式(阶)的瑞利波或勒夫波,各个模式在空间上对应着地震波在每层之间来回反射的不同路径[7]。基于各个模式的面波对地层参数的不同响应特征,采用多模式面波联合反演以提高反演精度是该领域的研究热点之一[8-9]。

近年来,面波多道分析方法(multichannel analysis of surface waves,MASW)在工程勘查领域受到广泛关注,它采用单点激发,多道等间距垂直(Z)分量检波器采集瑞利波,获得多模式的频散信息[6,10]。我们通常以频散能谱的强弱和连续性为标准,在能谱中拾取频散曲线。利用地震记录计算频散能谱的方法包括高分辨率Radon变换法、F-K变换法、相移法和矢量波数变换法等[11-13]。在噪声干扰及各个模式面波之间干涉的影响下,如果我们仅采用Z分量地震数据的瑞利波提取频散曲线,可能造成频散曲线出现不完整、不准确、模式误判等问题,那么最终得到的反演横波速度不准确[14-15]。改善Z分量地震数据的瑞利波在提取频散曲线方面的不足,以获得精确的横波速度模型,成为目前的研究重点之一。

均匀各向同性水平层状介质中的瑞利波偏振为垂直平面内的椭圆运动,其在径向和垂向上均有能量分布[16]。已有研究表明径向(R)分量地震数据包含了重要的瑞利波频散信息,且频散能谱分布与Z分量地震数据不同[17-18]。传统面波勘探仅采集Z分量地震数据中的瑞利波,获取关于介质的信息有限。通过分析R分量地震数据中的瑞利波频散信息,对Z分量地震数据中的瑞利波频散信息进行补充,可以得到更加完备、可靠的瑞利波速度频散曲线[19]。

数字地震仪和检波器的发展有助于采集高精度高质量的勒夫波数据,这使得勒夫波数据在浅表工程勘探、壳幔结构成像中的应用不断增加[20-22]。瑞利波和勒夫波频散曲线的联合反演可揭示更精细的近地表横波速度结构[16]。R分量和Z分量地震数据中的面波以瑞利波为主,切向(T)分量地震数据中的面波以勒夫波为主,因此多分量面波勘探能够以较低成本获取更多波场信息。近年来,多分量地震观测在油气藏勘探开发、地震监测中的广泛应用极大地推动了多分量面波观测技术的发展。对于如何利用多分量面波信息,DAL等[23-24]进行了探讨,并取得了一些研究成果。目前,多分量面波应用尚处于起步阶段,国内外成功应用的实例不多。为推动多分量面波技术在工程勘查、油气勘探、天然地震领域的应用,本文首先系统梳理了多分量面波技术的研究成果,然后对多模式速度频散曲线、多分量频散特征和偏振特征等方面进行了讨论,最后介绍了旋转分量在面波分离和面波频散分析等方面的应用,旨在促进多分量面波技术的深入研究与应用。

1 面波多模式频散

根据平面波理论,由相邻界面传播公式、自由表面边界条件及无穷远处辐射条件可推导出层状介质中瑞利波频散方程。通过求解瑞利波频散方程,可得到不同频率对应的相速度[25]。相速度是频率的多值函数,分别对应由不同路径的P波与SV波干涉形成的不同模式的瑞利波[7,26]。

1.1 理论相速度频散曲线计算

最初采用Thomson-Haskell矩阵算法[25]计算瑞利波理论频散曲线,但该算法存在计算速度慢、高频数值不稳定等问题。在此基础上,KNOPOFF[27]通过求解4n+2阶频散方程行列式,避免了数值不稳定问题。随后SCHWAB[28]采用快速Schwab-Knopoff方法通过行列式变换将某些层矩阵变形为块状对角阵形式,简化频散函数,降低计算量。KE等[29]提出了提高频散方程求解效率的根搜索算法,并提出Double Thomson-Haskell矩阵算法和正则Thomson-Haskell矩阵算法,分别用于计算各向异性介质的瑞利波和勒夫波理论频散曲线。此外,瑞利波频散方程求取方法还包括Abo-Zena算法[30]、δ矩阵法[31-32]、广义反射透射系数法[33-35]等。本文采用Knopoff算法[27]计算理论频散曲线。

1.2 面波的多模特性

XIA等[8]和罗银河等[9]的研究表明基阶瑞利波对浅层的横波速度更为敏感,而高阶瑞利波的穿透深度更大,多模式面波联合反演可以提高反演的精度和稳定性。近年来,多模式面波勘探已经有很多成功应用[36-37],在微动探测、背景噪声成像等被动源面波成像研究中,基阶和高阶面波频散曲线联合反演也受到广泛关注[38-39]。YAO等[40]研究发现不同模式的瑞利波联合反演可以得到准确的地壳和上地幔结构。

从实际地震数据中提取完整、准确的多模式面波频散曲线并非易事。受体波信号和强干扰噪声的影响,面波频散能谱会发生扰动,因此难以辨别面波模式[11]。图1展示了反射波对瑞利波频散能谱的影响[41]。从图1a可以看出,在无反射波影响时,可以清晰判别高阶瑞利波的阶数。从图1b可以看出,当瑞利波与深部反射波在时空域形成强干涉时,能谱极大值的位置发生偏离,无法判别椭圆圈中所示能谱的模式,这种情况下,如果直接根据图1b拾取频散曲线,会引起模式误判。此外,不同模式的瑞利波在地震记录中相互干扰,实际提取到的频散曲线往往表现为多个模式的叠加,容易引起模式跳跃,与理论频散曲线不完全对应,给面波模式的识别造成困难[42-44]。模式跳跃极易引发模式误判的问题,导致最终反演的横波速度不准确[14,42]。模式跳跃本质上反映了瑞利波各个模式下的激发能量相对大小随频率变化的关系[42]。对于含低速层的层状介质,MI等[45]认为软弱层间形成的高频导波无法从软弱层穿透到地表,不能形成对应的面波,因而造成频散能谱高频缺失,进而导致频散能谱的不连续或模式跳跃。同样地,实际提取的瑞利波频散曲线只是理论频散曲线中的一段,不完整、不准确的频散曲线会导致不稳定、不可靠的反演结果[15]。

图1 原始面波频散能谱(a)和受反射波干扰的面波频散能谱(b)

为避免模式误判,研究人员相继提出了一些解决方案。鲁来玉等[46]提出根据各模式位移的分布情况,识别频散曲线对应的面波模式;FOTI等[43]提出增加检波器个数,以减弱各模式的干涉;LU等[47]认为当最小炮检距大于0.5倍面波波长时,可获得较可靠的频散曲线;DAL等[18]对频散曲线的模式进行判别,直接对频散能谱进行反演;PAN等[48-49]提出无需识别面波模式的时空域面波波形反演方法,无需识别面波模式的反演方法虽然可以直接反演频散能谱或面波数据,但是运算量极大,并且对数据的信噪比要求高。

与理论频散曲线不同,视频散曲线考虑了各个模式下瑞利波的叠加效应,与实际提取的频散曲线具有良好的一致性[44]。LAI等[44]提出了在垂向点源激发时R分量和Z分量地震数据的瑞利波视频散曲线计算方法:

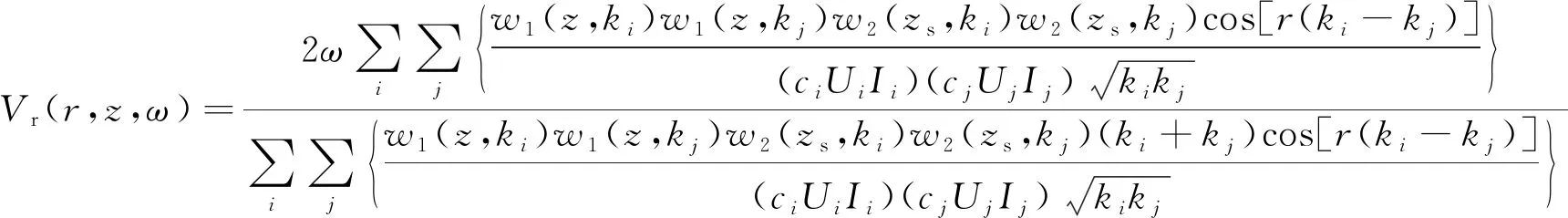
(1)

(2)

式中:Vr,Vz分别为R分量、Z分量地震数据瑞利波视频散曲线对应的相速度;w1,w2分别为R方向和Z方向的位移特征函数[50];i或j均为瑞利波的阶数;ki,kj为波数;ci,cj为相速度;Ui,Uj为群速度;Ii,Ij为瑞利波第一能量积分[50];r为偏移距;z,zs分别为检波点和炮点的深度。根据表1所示的模型1参数,得到的瑞利波理论频散曲线和Z分量的视频散曲线如图2所示,可以看出,在38Hz处,视频散曲线从基阶跳跃到第一高阶;在59Hz处视频散曲线从第一高阶跳跃到第二高阶。视频散曲线可用于预测多模式瑞利波的能量分布规律,研究多模式面波的叠加效应[51]。视频散曲线能直接用于反演横波速度结构,无需辨别面波的模式,避免了前述频散曲线的模式误判问题[52]。

表1 模型1参数

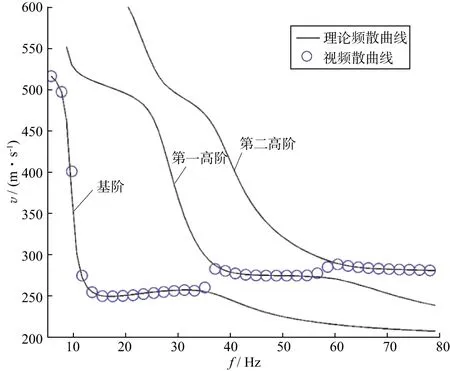
图2 根据模型1参数得到的瑞利波理论频散曲线和Z分量视频散曲线

2 多分量面波频散

传统面波技术因仅采用Z分量的瑞利波,故不足以完整描述面波在近地表的传播特征。随着多分量检波器和地震仪的应用,多分量观测已在油气藏勘探开发、地震监测中得到广泛应用[53-54],并在近地表工程地震中进行了一些有益的尝试。目前能够以较低成本获取更多速度频散信息及偏振特征,进而得到更准确的横波速度模型。

2.1 R分量、Z分量瑞利波频散特征

各个模式的瑞利波在R分量、Z分量的响应不同。CHEN[33]利用本征函数研究了瑞利波振动特征,发现对于同一个频散点,水平和垂直方向的本征位移曲线存在差异。QIU等[15]认为地表接收的各阶瑞利波在R分量、Z分量强弱分布不同,这造成了R分量、Z分量瑞利波频散能谱特征不同。在石油地震勘探领域,IKEDA等[19]利用R分量瑞利波补充了传统Z分量瑞利波中缺失的高阶瑞利波的频散信息。综合利用R分量、Z分量的地震数据,可提取到准确、完整的瑞利波多模式频散曲线,以减小模式误判的风险,提升横波速度反演精度[55]。

表2给出了模型2的参数[15],图3展示了根据模型2参数合成的R分量、Z分量瑞利波记录及其频散能谱。由频散能谱可见,R分量基阶瑞利波缺失,其它阶瑞利波分布在不同的频带,频带宽度相近;Z分量基阶瑞利波在6～39Hz占优,第三高阶以上的瑞利波能量很弱。为方便对比频散曲线的频带,我们将能谱值大于0.7的频带定为有效频带。同一模式下,R分量、Z分量瑞利波的频带不同,如R分量第二高阶瑞利波的频带为25～36Hz,而Z分量第二高阶瑞利波的频带为33～41Hz。R分量、Z分量瑞利波的频散特征互为补充,二者结合有助于得到完整的瑞利波频散信息。

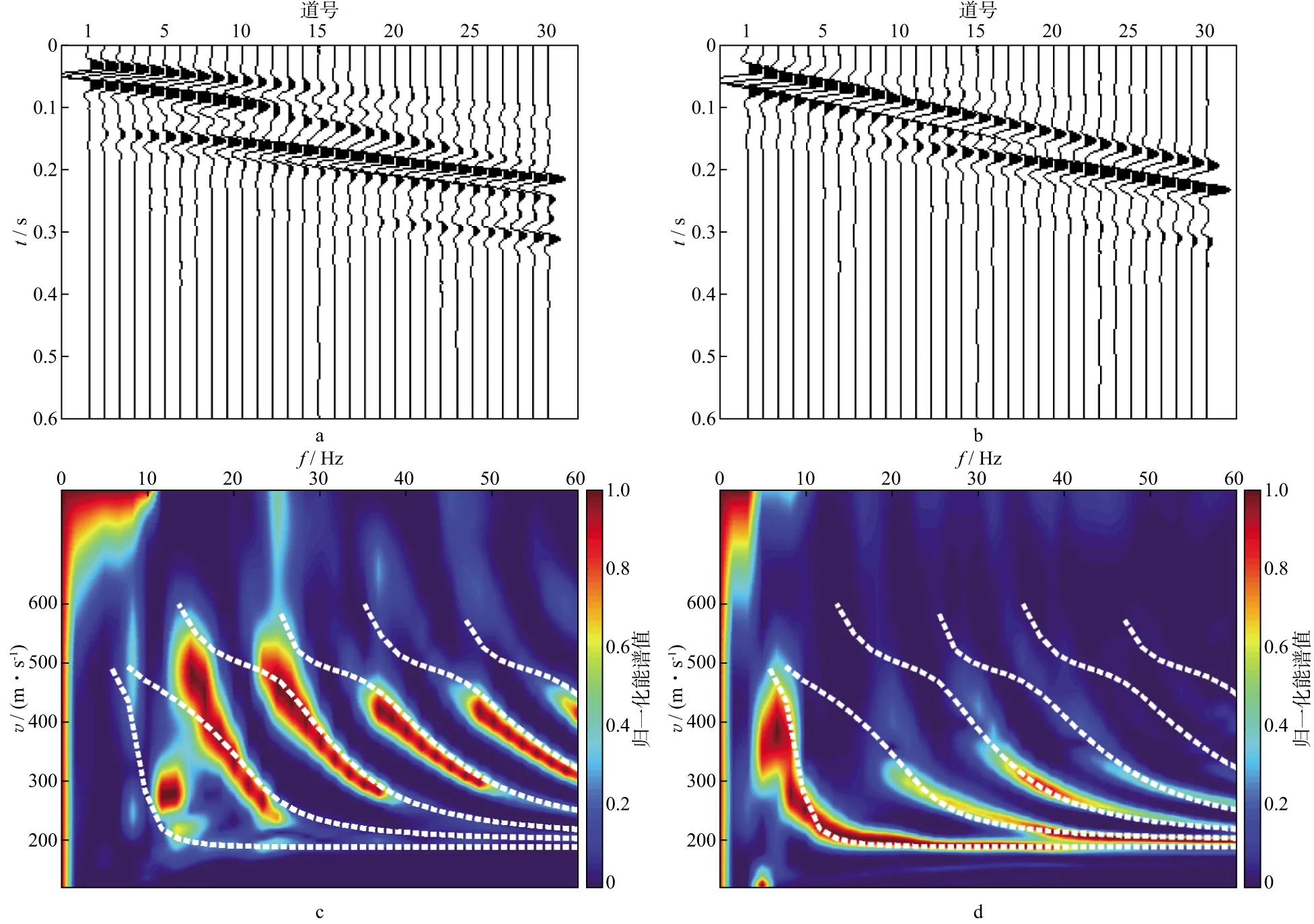
图3 根据模型2参数合成的R分量、Z分量瑞利波记录及其频散能谱[15](图中白色虚线是理论频散曲线)

2.2 勒夫波频散特征

与瑞利波不同,勒夫波的速度频散特征只取决于横波速度、密度和层厚度,而与纵波速度无关,这使得勒夫波具有与瑞利波不同的频散特征[50]。利用Knopoff算法[27]计算模型1的瑞利波和勒夫波理论频散曲线如图4所示,不难发现,与瑞利波“之”字形的频散曲线相比,勒夫波的频散曲线形态较简单。此外,勒夫波频散能谱清晰,易于拾取频散曲线,不会产生模式误判的问题[56]。XIA等[21]提出了勒夫波多道分析方法(multichannel analysis of Love waves,MALW),该方法通过勒夫波频散曲线提取和反演,获得近地表横波速度模型。与瑞利波频散曲线反演相比,勒夫波频散曲线反演对初始模型的依赖较低,反演结果更稳定[21]。

2.3 多分量面波勘探

勒夫波频散曲线形态简单,在地层细节刻画等方面不及瑞利波精细[18]。YIN等[57]研究表明,相同波长的勒夫波和瑞利波对深度的敏感性不同。勒夫波和瑞利波含有不同的频散信息,因此采用瑞利波和勒夫波的联合反演有助于获得准确的近地表横波速度模型。在天然地震成像研究中已有采用瑞利波和勒夫波联合反演的应用实例[20]。因R分量和Z分量瑞利波频散信息互补,故使用三分量(three-component,3C)检波器进行面波采集,能够获取频散信息丰富的瑞利波和勒夫波数据,且不增加采集工作量。

在工程面波勘探中,常用震源为锤击震源和可控震源。根据震源的激发方向与测线方向的不同,震源可分为垂向力源(Sz)、径向力源(Sr)、切向力源(St)。多分量震源能够同时激发3个方向的力源,但传统多分量震源在各个激发方向上震源耦合不同,导致波场在各个方向上的振幅大小关系失真,这给多分量数据处理造成困难[58]。3C Galperin震源解决了上述问题,并在面波数据采集中得到成功应用[58-59]。将该3C震源与3C检波器组合应用,可以得到9个分量的地震记录,其面波的类型如表3所示[59-60]。传统面波勘探采用垂直力源激发、Z分量检波器接收的采集方式,只获得一个瑞利波分量(Sz-z);而3C震源激发、3C检波器接收的采集方式可获得包含5个分量的面波数据,包括4个瑞利波分量(Sr-r,Sr-z,Sz-r,Sz-z)和一个勒夫波分量(St-t),经反演可获得更准确的横波速度模型[61]。

图4 模型1瑞利波(a)和勒夫波(b)的理论频散曲线

表3 不同方向的震源在不同测线产生的不同分量地震记录的面波类型

2.4 多分量面波数据联合处理

国内外研究者从不同角度给出了多种处理多分量面波数据的方法。DAL等[16]分别提取了R分量、Z分量瑞利波频散曲线,而后组合得到瑞利波频散曲线,对于干扰较强的地震数据,上述处理方法仍可能造成模式误判的问题,还容易造成提取的频散曲线不准确。PAN等[59]提出将各分量瑞利波频散能谱叠加,以提高瑞利波频散能谱的准确性。叠加处理的前提是各个分量所包含的频散信息一致,对于分量频散差异较大的地震数据,这种处理方法难以达到预期的效果,考虑到R分量、Z分量瑞利波频散信息的互补性,利用复矢量数据频散提取方法,将R分量、Z分量组合为复矢量,采用高分辨率Radon变换算法计算复矢量数据的频散能谱[15]。与传统Z分量瑞利波频散曲线的提取方法相比,基于复矢量数据的频散提取方法能够削弱噪声干扰,避免模式误判,获得更完整、可靠的频散曲线,但该方法只能处理同一震源激发的R分量、Z分量数据,无法同时处理表3所示的包含4个分量的瑞利波数据。DAL等[18]为Sz-r,Sz-z,St-t 3个分量的面波数据分别构建了3个目标函数,然后采用Pareto优势准则优化求解,最终实现了包含R分量、Z分量瑞利波和T分量勒夫波的三分量面波数据联合反演,这为多分量面波联合反演提供了新的研究思路。

3 瑞利波偏振特征

3.1 面波偏振特征与波场分离

在层状介质中,瑞利波的偏振特征较为复杂[50]。RENE等[62]分析了勘探地震数据中基阶瑞利波和第一高阶瑞利波的椭圆极化差异,发现基阶瑞利波呈逆时针偏振,偏振角近于90°;第一高阶瑞利波呈顺时针偏振,偏振角近于0。MA等[63]对沉积盆地地区的背景噪声互相关数据进行了研究,也发现基阶瑞利波呈逆时针偏振,而第一高阶瑞利波呈顺时针偏振。

利用面波的偏振特征可实现多分量地震数据的波场分离。石油地震勘探和天然地震研究中已有很多利用面波和反射波偏振形态的差异实现面波和反射波分离的应用实例[64-66]。利用基阶瑞利波和第一高阶瑞利波偏振椭圆的旋转方向差异,可以设计偏振滤波器实现基阶瑞利波和高阶瑞利波的分离[67]。利用偏振特征差异还可以分离勒夫波和瑞利波[68]。此外,瞬时相位差也可以用于面波和反射波的波场分离[66],但地震数据和背景噪声数据的瑞利波频率较低,关于瑞利波偏振椭圆旋转方向的假设不完全适用于10～80Hz的高频瑞利波[24,69-70]。对于10～80Hz的高频瑞利波,BOAGA等[55]和QIU等[15]的研究表明,多层介质各模式瑞利波的偏振椭圆的旋转方向和椭圆率均随频率变化,因此很难根据偏振特征将各模式瑞利波相互分离。

3.2 椭圆率频散

IKEDA等[71]提出了多模式瑞利波椭圆率的计算公式。多模式瑞利波椭圆率的理论计算结果表明,多模式瑞利波的椭圆率是频率的函数,不同模式下的椭圆率频散特征存在差异[15]。研究表明,瑞利波椭圆率与介质横波速度结构密切相关[55,72]。张立等[73]的研究表明,瑞利波水平分量和垂直分量的频谱比(简称HV谱比)实质上为瑞利波椭圆极化的频散特征,HV谱比与介质泊松比相关。LIN等[74]认为,与频散曲线相比,瑞利波椭圆率对浅层结构更敏感。在壳幔结构成像中,HV谱比与速度频散曲线联合反演可以得到更准确的地壳和上地幔速度结构[75]。MI等[76]从多道面波记录中准确提取了瑞利波HV谱比曲线,并发现其HV谱比曲线的峰频和槽频对介质纵、横波速度比和界面深度敏感。此外,在岩土工程领域,椭圆率和速度频散曲线的联合反演可以更准确地估计基岩深度[17,77]。目前对椭圆率频散的研究,多基于瑞利波主要能量来自于基阶瑞利波的假设;多模式瑞利波的椭圆率频散对介质速度结构响应的影响是未来的研究方向之一。

4 旋转分量记录的面波

地震波传播时,波场的质点运动包括了平动、旋转和变形,为了完整描述波场特征,必须研究地震波的3个旋转分量[78]。其中,旋转张量ω定义为[79]:

(3)

旋转分量和平动分量共同组成了6个分量的地震观测数据,构成了地震波场包含6个自由度(six degree-of-freedom,6-DOF)的矢量观测数据,该数据可用于面波的识别与分离[79]。EDME等[85]认为旋转分量Rx或Ry以面波为主,利用该分量地震数据生成面波模型,通过自适应相减法可压制平动分量的面波。受协方差矩阵秩的限制,对单台站的地震数据采用平动三分量偏振分析法无法分离时域重合的波场;而六分量地震数据由于包含了水平视速度信息,提升了协方差矩阵的秩,因此可以有效分离时域重合的波场[86]。SOLLBERGER等[86]利用多重信号分类算法获取六分量偏振信息,识别和分离面波。BARAK等[87]将单台站的六分量地震数据组合为矩阵,利用奇异值分解法识别波场偏振特征和分离面波。

因瑞利波对高层建筑物的影响范围广,破坏性强,所以地震工程中对高楼地震响应的分析,大多情况下直接评估瑞利波引发的震动[88-89]。目前在工程设计中,如果只考虑平动,忽略旋转,容易导致近场建筑结构的振幅响应估计不足[81]。为准确评价地震响应,有必要同时考虑平动和旋转[88]。因此,利用六分量面波评价高楼的地震响应,将成为该领域未来研究方向之一。

5 多分量面波的发展趋势

在石油地震勘探领域,面波既可作为反射波勘探的干扰,也可用于近地表结构调查[90-91]。为压制面波,需准确把握面波的运动学和动力学特征。传统单分量面波压制方法只利用面波的速度、频率等特征,而多分量面波压制方法可以利用面波的偏振特征,波场分离更彻底且能有效保持矢量特征[65]。与三分量偏振分析方法相比,利用六分量地震数据的偏振分析方法可以更好地压制面波[86]。在石油地震勘探领域,利用六分量地震数据分析面波和反射波的属性差异,识别和分离面波,将成为未来重点研究方向之一。

在石油地震勘探中,为消除近地表地震-地质条件的影响,需准确把握近地表结构。在近地表结构调查的各种方法中,面波成像方法无需增加勘探成本,即可获得较为准确的近地表速度模型,因此受到广泛关注[4,90]。它主要利用地震数据中的瑞利波获得近地表横波速度模型。目前石油地震勘探中,利用Z分量瑞利波不足以完整地描述面波在近地表的传播和振动特征。利用多分量地震勘探数据,获得瑞利波和勒夫波速度频散、偏振、衰减特征,可对近地表介质速度模型和粘弹性等属性获得更准确的认识。针对旋转分量和平动分量的面波频散特征,研发面波频散曲线提取和反演的方法是今后的研究方向之一。

6 结论

本文梳理了国内外多分量面波理论和相关方法技术的研究成果,从多分量面波相速度频散特征、面波偏振特征等方面展开论述,综合调研分析得出以下结论。

1) 虽然地表接收的面波存在多个发育模式,但是单分量面波的频散信息不完整,因此提取的频散曲线可能不准确。

2) 不同分量的面波数据包含了不同的速度频散信息,多分量面波处理、反演有助于获得更准确可靠的横波速度模型。

3) 面波的椭圆率等偏振属性具有频散特征,结合速度的频散特征,能够更好地确定浅层介质的速度模型。

4) 六分量地震数据包含更丰富的面波运动学和动力学特征。因此六分量面波研究为面波频散提取和分离等方面提供了新思路。