虚拟波场变换方法在电磁法中的进展
林 超, 严家斌
(1.中南大学 地球科学与信息物理学院,长沙 410083;2.有色金属成矿预测与地质环境监测教育部重点实验室,长沙 410083)
0 引言
电磁法勘探是基于分析电磁波在大地介质中的传播特性,达到研究地下地质体的赋存或构造特性的目的。通过使用天然或人工场源在大地中激发的交变电磁场,研究电磁场的时间和空间分布,分析观测到的电磁响应信号,来获得地下目标体电性分布的一种勘探方法[1]。在工程勘查[2-3]、资源勘探[4-5]、地下水探测[6-7]、地质填图[8-9]和矿井灾害预测[10-11]等方面都有广泛地应用。电磁法方法的研究与应用是基于麦克斯韦方程组,为了避免电磁场特性的复杂分析以及降低各种干扰,提高电磁法方法的实用性,大部分电磁法方法都是采用准静态近似的麦克斯韦方程组(如瞬变电磁法、海洋可控源电磁法等),但扩散场方程是不利于成像的,为了满足高分辨率和精细成像以及快速解决复杂问题的要求,必须寻找新的数据处理方法,由此开展了虚拟波场变换研究。
虚拟波场变换方法是指通过数学上的积分变换,将麦克斯韦扩散方程转换为与电磁波类似的虚拟波动方程,在虚拟波场中进行计算和分析,该方法的初始研究是借鉴波动方程的性质,通过虚拟波场变换将地震中一些成熟的方法引入到电磁法的数据解释中,提高电磁法数据解释的分辨率,后来研究发现它在提高数值模拟的计算效率以及其他方面也可发挥重要作用。
电磁法虚拟波场变换的方法研究开始于上世纪70年代。Kunetz[12]首先发现了扩散的电磁场和波动方程之间存在着联系;Lavrent'ev[13]用数学方法证明并提出了扩散方程和波动方程之间的转换关系;Lee等[14]通过在准静态扩散的麦克斯韦方程组中引入“q函数”实现了扩散电磁场到虚拟波场的转换,将虚拟波场变换方法运用到电磁法中;de Hoop[15]通过借助格林函数,在麦克斯韦方程组中应用拉普拉斯变换,推导出了扩散电磁场和虚拟波场的变换关系;Maaø[16]将最初的麦克斯韦方程通过数学变换,转换到较低频率依赖性的复频率域中,提出一种基于复频率域的虚拟波场方法;Mitte[17]在对麦克斯韦方程组进行变换时利用傅里叶变换,使得虚拟波场的变换过程更简单。伴随着虚拟波场变换理论方法的逐渐完善,虚拟波场的应用也越来越受到重视。为了充分认识波场变换技术和它的应用价值,这里对虚拟波场变换的方法原理以及应用做了简要的分析与综述。
1 虚拟波场变换理论
虚拟波场变换方法一般用在低频电磁法中,从麦克斯韦基本的扩散方程出发,对于准静态情况下的时域扩散场,麦克斯韦方程组可以表示为:
▽×H(r,t)-σ(r)E(r,t)=-J(r,t)
(1)
▽×E(r,t)+μ∂tH(r,t)=-K(r,t)
(2)
式中:H(r,t)表示时间域磁场分量;E(r,t)表示时间域电场分量;J(r,t)表示外加电性源;K(r,t)表示外加磁性源;r表示空间变量;σ(r)表示电导率;μ表示磁导率。式(1)和式(2)经过数学物理变换最终可变为如下形式:
(3)
(4)
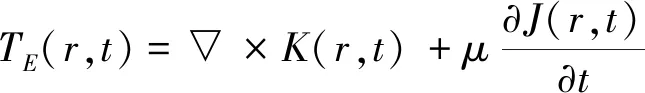
(5)
(6)
式中:FE(r,g)为虚拟波场中的电场;FH(r,g)为虚拟波场中的磁场;SE(r,g)和SH(r,g)分别为虚拟波场中电场和磁场的源时间函数;c为虚拟波波速,与电导率、磁导率有关;g为虚拟波场中的时间变量与扩散场的时间对应;r为虚拟波场中的空间变量和扩散场中的一致。需要注意的是,从扩散场到虚拟波场的变换方法并不是唯一的,主要体现在引入的函数上,式(1)~式(6)是麦克斯韦扩散方程到虚拟波动方程的变换形式,通过积分变换可得虚拟波场恢复到时域扩散场的对应关系,其对应关系由如下方程表示:
(7)
(8)
(9)
(10)
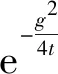
2 虚拟波场变换的方法
虚拟波场变换中引入不同的函数就会有不同的变换形式以及波和扩散场之间的对应关系。目前,已知的波场变换方法有三种:Lee[14]提出的“q域法”方法、Maaø[16]提出的基于复频率的方法及Mittet[17]提出的方法。
2.1 q域法
q域法是通过在时域扩散的麦克斯韦方程组中引入定义的“q函数”,实现了虚拟波场的变换,然后通过积分变换得到波场到扩散场的对应关系,大致过程如下:
定义“q函数”:
(11)
式中:ω0为比例伸缩系数;t′为虚拟波场的时间。将“q函数”引入到时域的扩散麦克斯韦方程组(1)、方程组(2)中,即用q替代方程中的时间t,得到一组虚拟波场方程:
(12)
(13)
虚拟波场与扩散场的对应关系为:
(14)
H″(r,q)=H′(r,q)
(15)
J″(r,q)=J′(r,q)
(16)
(17)
将式(14)~式(17)代入到式(12)~式(13)之中可得重构的虚拟波动方程:
-▽×H″(r,q)+σ(r)∂qE″(r,q)=-J″(r,q)
(18)
▽×E″(r,q)+μ∂qH″(r,q)=-K″(r,q)
(19)
最后通过积分变换可从虚拟波场恢复到扩散场:
(20)
(21)
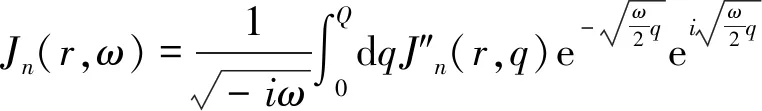
(22)
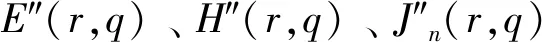
2.2 基于复频率的方法
复频率域方法是通过在频率域的麦克斯韦扩散方程组中引入定义的复频率函数实现虚拟波场的变换,再通过积分变换从虚拟波场恢复到扩散场,其过程如下:
复频率函数定义为:
iω=iω′(1-iω′a)
(23)
式中:a为常数,它的取值影响着时间步长的大小,一般根据实际情况选取合适的值,但不能取小于零的数;ω′为虚拟的角频率;ω为扩散场的角频率。将复频率函数iω带入到频率域麦克斯韦扩散方程组中,其他量保持不变:
-▽×H(r,ω)+σ(r)E(r,ω)=-J(r,ω)
(24)
▽×E(r,ω)-iω′(1-iω′a)H(r,ω)=
-K(r,ω)
(25)
在虚、实波场中对应关系为:
E′(r,ω′)=E(r,ω)
(26)
H′(r,ω′)=(1-iω′a)H(r,ω)
(27)
J′(r,ω′)=(1-iω′a)J(r,ω)
(28)
K′(r,ω′)=K(r,ω)
(29)
利用对应关系可得重构的虚拟波动方程:
-▽×H′(r,ω′)+(1-iω′a)σ(r)E′(r,ω)
=-J′(r,ω′)
(30)
▽×E′(r,ω′)-iω′μH′(r,ω) =
-K′(r,ω′)
(31)
通过积分变换得到虚拟波场恢复到扩散场的对应关系为:
(32)
(33)
(34)
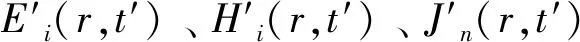
2.3 Mittet方法
通过定义一个虚拟的介电常数,将虚拟介电常数代入到频率域扩散麦克斯韦方程组中,然后直接在方程中乘以一个适当的函数,最后通过定义一个虚拟的角频率以及对应关系实现虚拟波场的变换,该方法从虚拟波场恢复到扩散场需要利用格林函数,其过程如下:
定义一个虚拟的介电常数:
(35)
式中:ω0为比例伸缩系数,它的取值也影响时间步长的大小,需要根据实际情况选取合适的值,且不能小于零。将虚拟的介电常数代入到频率的扩散麦克斯韦方程组中可得:
-▽×H(r,ω)+2ω0ε′(r)E(r,ω)=
-J(r,ω)
(36)
▽×E(r,ω)-iωμH(r,ω)=-K(r,ω)
(37)
(38)
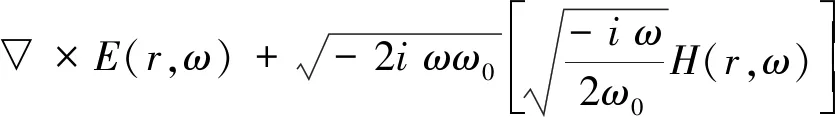
=-K(r,ω)
(39)
定义虚拟波动场中的角频率以及对应关系:
(40)
E′(r,ω′)=E(r,ω)
(41)
(42)
(43)
K′(r,ω′)=K(r,ω)
(44)
式中:ω′为虚拟波场的角频率,将式(40)~式(44)代入到式(38)或式(39)之中可得频率域的虚拟波动方程,经过傅里叶变换可得时域的虚拟波动方程:
-▽×H′(r,t′)+ε′(r)∂t′E′(r,t′)=
-J′(r,t′)
(45)
▽×E′(r,t′)+∂t′H′(r,t′)=-K′(r,t′)
(46)
从时域波场恢复到时域扩散场的过程如下:
首先,根据类傅里叶变换积分将虚拟波场中的时域电磁场响应变换到虚拟波场中的频率域电磁场响应:
(47)
(48)
(49)
其次,构造格林函数:
(50)
(51)
最后,通过对所得格林函数进行傅里叶变换可得到真实扩散场的时域电磁响应:
(52)
(53)
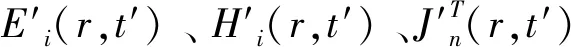
3 虚拟波场的应用
虚拟波场方法可以有效地提高数值模拟的计算效率,目前主要针对三维的数值模拟和拟地震反演成像等数据处理与解释方面。
3.1 在提高数值模拟计算效率方面的应用
虚拟波场变换方法能提高数值模拟的计算效率主要是基于它满足的波动方程(式(5)~式(6))的性质,在扩散电磁场中,由于电磁波在地下介质中的传播的速度很大,利用有限差分进行数值计算时,需要很小的时间步长才能满足稳定性条件。在虚拟波场中满足的方程是波动方程,虚拟波的波速不再是现实中电磁波波速,可以选择较小的虚拟波波速来获得较大的时间步长且满足它的稳定性条件,这使得在虚拟波场中有限差分法的计算效率很高,最后再恢复到扩散场。积分方程和有限元等数值模拟方法也可以求解,只是显示有限差分法具有占用内存小,建模简单等优势,所以在该方法中比较适用。
Maaø[16]提出了一种基于复频率的波场变换方法之后,在虚拟波场中利用有限差分方法求解的巨大时间效益才体现出来。Støren 等[18]在利用局部梯度优化方法对海洋可控源数据进行三维反演时,在三维正演建模过程中采用Maaø[16]提出的虚拟波场变换方法,加快了失配梯度的计算速度。Mittet[17]提出了一种相对更简单的虚拟波场变换方法,其主要是在Maaø提出的基于复频率的波场变换方法上进行改进,并采用傅里叶变换去代替Lee等[14]的拉普拉斯变换。Mittet[22]将该方法引入到海洋大地三维数据反演的正演建模之中,同时,在正演计算过程中提出了一种非均匀网格垂直节点间距设计的标准以及采用了卷积完全匹配层进行边界条件的处理,减少了计算区域的尺寸,提高了计算效率。Imamura等[19-20]在对海洋可控源电磁法三维全波形反演研究时,在正演建模时采用了Mittet[17]提出的虚拟波场变换方法,提高了正演的计算效率。Liu等[21]将Mittet[17]提出的虚拟波场变换方法用于瞬变电磁实测数据的二维正演,取得了良好效果。Hu等[23]将该方法引用到三维瞬变电磁的数值模拟,在正演计算中利用卷积完全匹配层处理边界条件,并且在计算时将空气层作为有限高阻引入到计算区域内,实现了对带地形模型的模拟,最后将所得结果和SLDMA方法的对比,两者具有良好的一致性,证明了该方法的有效性和计算的高效性。
3.2 虚拟波场拟地震反演成像的应用
虚拟波场拟地震反演成像主要是利用虚拟波场中与电磁波波传播的有关特性,它的实质是通过数学上的积分变换提取电磁波中与波传播有关的信息,使得虚拟波场类似于地震子波具有诸如反射、折射、衍射和透射等特征。虚拟波场拟地震成像可简单的概述为:根据扩散场和虚拟波场的对应关系,利用奇异值分解等优化算法将扩散电磁场信号转换成虚拟波信号,然后借助于偏移成像、层析成像等地震方法以及一些其他的方法来对获得的虚拟波信号进行成像等数据处理。
虚拟波场拟地震成像的应用最早开始于20世纪90年代,Lee等[24]提出利用奇异值分解来进行波场逆变换,从获得的稳定波形中估计源到接收器的旅行时间,再用获得的旅行时间进行层析成像来反映地下电阻率结构,并通过费马原理的两点光线追踪算法来进行高效迭代。Lee等[25-26]提出一种直接从频率扩散场垂直磁场中提取旅行时间的方法,在虚拟波场中利用提取的旅行时间进行非线性层析成像,成功地估算了合成电磁数据的电阻率,并在实测数据中应用,证明了该方法的有效性。Kusuda等[27]在研究如何提高海洋可控源电磁法对甲烷水合物检测时,利用奇异值分解的方法,将海洋可控源数据转换成虚拟波场数据,分离出甲烷水合物异常区的波形。利用分离出的波形进行成像分析,提高了海洋可控源电磁法对甲烷水合物的分辨率。Amani等[28]提出利用地震中的逆时偏移成像和克希霍夫偏移成像的方法对虚拟波场变换得到的稳定波形成像,并将这两种方法用于海洋可控源电磁法数据的二维反演成像,通过综合比较得出逆时偏移成像的精度较高。
国内的瞬变电磁拟地震成像开始于20世纪90年代,研究方向可分为:波场优化算法、反褶积压缩子波宽度、三维曲面延拓成像、合成孔径成像。波场优化算法主要是用于在波场逆变换中,减少不适定问题带来的高度欠定的影响,从而使波场逆变换获得的波形稳定,在这方面的研究可参考文献[29-32];反褶积压缩子波宽度是削弱波场逆变换中核函数随时间的增加分布范围增大带来的波形较宽的问题,其实是对波场逆变换中获得的波形进行滤波处理,在这方面的研究可参考文献[33-34];三维曲面延拓是为了消除地形起伏带来的曲面以及测线不规则对反演成像带来的影响,提高反演成像的分辨率。在这方面的研究可参考文献[35-37];合成孔径处理是借鉴合成孔径雷达成像的方法,即通过利用机载真实孔径发射线圈与目标的相对运动,把尺寸较小的真实天线孔径用数据处理的方法合成一较大孔径的发射线圈,提高它的分辨能力和穿透力,由于雷达满足的偏微分方程和虚拟波场满足的偏微分方程都是波动方程,所以该方法可用于虚拟波场逆变换反演成像中,在这方面的研究可参考文献[38-40]。
3.3 其他方面的应用
在利用有限差分求解方程时,对函数的一阶偏导数的离散一般用含算子系数的中心差分近似来表示, Pasalic等[41]研究发现,可以通过对算子系数进行最优化然后取高阶的差分算子来减少离散网格的尺寸,并将该方法应用到虚拟波动方程的离散中,进一步提高了虚拟波场-有限差分法的计算效率。Imamura等[42]在虚拟波动方程离散上采用了粒子法,并提出了交错粒子法和非交错粒子法,通过模拟对比,交错粒子在数值上比非交错粒子有效率更高,主要是在同等的空间间隔中,交错粒子只需要一半的数目就能达到和非交错一样的精度。Mittet[43]在对虚拟波域的波场和地震波波场关系研究过程中,为了使两者条件一致,利用声波来近似代替地震波,通过对虚拟波场中的波形和声波波形的分析,证明了地震波场和海洋可控源电磁波场之间的相似性,以此来了解从虚拟波域到扩散域的转换效果。
4 虚拟波场存在的问题
虚拟波场变换是通过数学上的变换实现的,从式(7)~式(10)可知,它有两个过程:①波场到扩散场的正变换;②扩散场到虚拟波场的逆变换。虚拟波场方法的主要应用思路基本上都是围绕这两个不同的过程。但是这两个不同的过程各有不足,在逆变换中,获得的虚拟波类似于地震子波一样具有传播、反射、透射的特征,虽然在理论模型和一些实际应用中验证确实可行,实际上它是存在着一些问题的,例如:逆变换是第一类Fredholm型算子方程的反问题,它本身是非常复杂的,现在一般的解法都是求线性逼近系统的最小二乘解,但是这种求解方法会带来一定的误差,该误差很难估计;两种波场的物理背景不同,一个是客观存在的波场,一个是由数学变换得到的虚拟波场,将地震方法用于虚拟的波场中是否能反映出地下真实情况;扩散场具有频散和吸收的特性,十分复杂,用简单的虚拟波场来代替是否符合实际情况,以及扩散场的波速跟频率有关,而虚拟波场中的波速跟频率无关,这种不一致带来的影响等。在正变换中,虽然最终恢复到扩散场,但是在恢复过程中,积分变换带来的误差也很难估计,以及可能会引入高频成分、噪声等干扰因素。
5 结论
笔者详细介绍了虚拟波场变换的基本原理和方法,评价了它的优缺点,并对其在地球物理中的应用做了综述。虚拟波场在现实中是不存在的,在应用中,从扩散场到虚拟波场的变换相当于一个提取电磁波中有用信息的过程,虚拟波场相当于一个包含必要信息的容器。该方法为基于麦克斯韦扩散方程的电磁法方法的数据解释提供了高效的数值模拟和新的思路,有助于提高数据解释的效率和分辨率,丰富了电磁法数据解释的方法。
致谢:
感谢评审专家们提出的中肯的有建设性的修改意见,对本文的改进有很大的帮助。

