基于ESO的三相PWM整流器电流滑模控制研究
陈传林,肖文勋,刘毓鑫
(华南理工大学电力学院,广东 广州 510640)
电压型PWM整流器(VSR)的交流电流谐波小,直流侧电压恒定,可实现单位功率因数运行及能量的双向流动,得到了广泛应用[1]。
常规控制策略将PWM整流器近似为线性系统,并采用线性理论进行研究[2-4],忽略了整流器的强非线性,难以达到理想控制效果。近年来,国内外学者提出了多种非线性控制方法[5-10],并将其应用于整流器的控制中,以弥补线性控制的不足。其中,滑模控制较简单,鲁棒性强,应用广泛[11-13]。常规的滑模控制方法通常设计很大的切换增益,以保证系统的鲁棒性,但这也加剧了系统抖振。
针对上述矛盾,该文引入扩张状态观测器(ESO)对三相PWM整流器系统的总扰动进行观测,并将观测值补偿到电流滑模控制器中,同时设计了新的滑模趋近律,保证系统的强鲁棒性和快速的电流跟踪能力并削弱电流的抖振,降低了电流谐波含量,通过仿真和实验进行了验证。
1 三相PWM整流器的数学模型
图1是三相电压型PWM整流器的主电路。其中,L为交流侧电感,R为电感的等效内阻,C、RL、uO分别为直流侧电容、负载电阻、直流侧电压,ia、ib、ic为交流侧输入电流。设ea、eb、ec为三相对称的电网电压,根据基尔霍夫定律,得到三相VSR在三相静止坐标系下的数学模型为:

式中,Sa,Sb,Sc分别表示整流器三相桥臂开关管的开关函数。其中:S=1代表对应的桥臂上管导通,下管关断;S=0代表对应的桥臂下管导通,上管关断。

图1 三相电压型PWM整流器主电路
文中采用基于两相同步旋转坐标的滑模控制策略,对三相静止坐标系下的数学模型进行等功率旋转坐标变换后,得到的两相同步旋转dq坐标系下的数学模型为:

式中,ud=SduO、uq=SquO,其中:Sd、Sq分别表示 d-q坐标系下三相桥臂开关管的开关函数;ed、eq和id、iq分别为电网的电压和电流的d、q分量;ω为电网电压的角频率。
2 基于ESO的电流滑模控制
2.1 传统电流滑模控制器
滑模控制器的设计步骤分为两步:第一步是选取适当的滑模面,第二步是设计合适的滑模控制趋近律。在满足滑模到达条件的控制律作用下,系统将在有限时间内从任意初始状态到达滑模面,并做滑模运动,此时的跟踪误差逐渐收敛为零。
传统的d-q坐标系下的电流滑模面为:

传统的等速趋近律为:
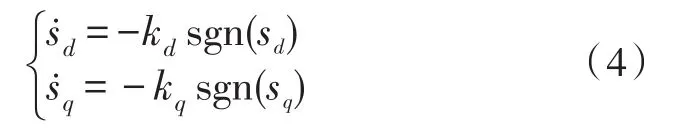
结合式(2)~(4)可以得到电流滑模控制律,如下:

下面讨论在传统滑模控制器的控制下,系统的鲁棒性与抖振之间的矛盾以及引入扩张状态观测器的必要性。当出现参数摄动或外来扰动时,式(2)描述的数学模型变为:

其中,vd和vq分别为未知扰动的d、q分量。
将式(5)代入式(6),可得:

由式(7)可知,为了保证系统在扰动下的稳定性,系统需满足滑模到达条件:

切换增益系数必须满足:

然而在工程实际中,系统扰动往往不可预先获得,故在传统滑模控制器的设计中,将扰动的上界设为一个很大的值[14]。由式(9)可知,需设计很大的切换增益以确保系统在大扰动下稳定。然而由式(7)可知,在未出现大扰动时,系统趋近滑模面的加速度很大,从而导致到达滑模面时在惯性作用下高速而频繁穿越滑模面,形成抖振[15]。因此,传统等速趋近律滑模控制器的鲁棒性与系统抖振之间存在矛盾。为了解决这一矛盾,有必要引入ESO对系统的未知干扰进行观测,并将其补偿到控制律中,设计性能更好的趋近律。
2.2 扩张状态观测器
根据扩张状态观测器理论[16],令VSR系统的状态变量为 x1=[idiq]T,定义系统的外扰为 v(t)=[vdvq]T,将电网电压和系统的参数及未知外扰一起扩张为新的状态变量,记:x2=[(ed-Rid+ωLiq+vd)/L(eq-Riq-ωLid+vq)/L]T,x2被视为系统的总扰动,则dq坐标系下VSR的电流状态空间方程可以写成:

其中,b0=-1/L,u=[uduq]T,d(t)是未知函数。根据式(10),可以构造如下二阶扩张状态观测器:

式中:z1=[z1dz1q]T和 z2=[z2dz2q]T分别为状态量x1和扩张状态量 x2的观测值。β1、β2、α是观测器的设计参数,均为大于零的常数。扩张状态观测器的扰动观测值z2包含了对电网电压扰动、系统参数摄动以及未知外扰的观测,用z2进行扰动补偿后,系统能获得很好的抗各种扰动的能力。
2.3 新型电流滑模控制器设计
通过扩张状态观测器可以得到扰动的观测值z2,得到带扰动补偿的等速趋近律电流滑模控制器控制律,其可表示为:

传统的等速趋近律在滑模面附近的切换增益大,导致系统做滑模运动时抖振较大,因此,文中设计了如下的新型趋近律:

其中,kd和kq是大于零的常数,e为自然数。
比较式(4)、式(13),由式(12)可知,基于扩张状态观测器的新型滑模控制器表达式为:

由新型趋近律的表达式可知,当系统状态远离滑模面时,有|sd|>>0、|sq|>>0,则电流的 d、q分量的运动加速度的绝对值约为kd和kq,系统以很大的加速度趋近滑模面,使系统有较强的鲁棒性和动态性能。当系统状态运动到接近滑模面时,有|sd|≈0、|sq|≈0,电流的d、q分量的运动加速度的绝对值约为0,系统以很小的加速度沿滑模面运动,从而避免了系统频繁而高速地穿越滑模面,抑制了抖振。将新型滑模趋近律与ESO的扰动补偿结合,可以保证系统在大扰动下的鲁棒性。
3 系统双环控制方案
系统采用双环控制,如图2所示,其中电压外环采用常规的PI控制,以使直流侧电压恒定跟踪参考值并向电流内环提供有功电流参考值;电流内环通过ESO观测误差并由式(14)确定的滑模控制器得到调制电压,调制电压经过坐标变换和空间矢量脉宽调制后得到相应的开关信号。

图2 系统控制方案
4 仿真与实验
4.1 仿真验证
在Matlab/Simulink环境下对电流环的性能进行测试,仿真参数如表1所示。

表1 仿真参数
图3为采用基于ESO的新趋近律滑模控制改进方案时,三相PWM整流器到达稳态后的电网a相电压、电流波形。可知,电流与电压同相,实现系统单位功率因数运行。

图3 改进方案的系统交流电压电流波形
稳态时改进方案和传统方案的系统交流电流d、q分量的波形如图4所示,传统方案为图2中无ESO的等速趋近律双环控制方案。可知,采用改进方案和传统方案的系统,其交流电流的d、q分量都能跟踪给定值,但采用改进方案的系统的电流抖动比采用传统方案的系统小。说明改进方案抑制了系统的电流抖振,电流跟踪效果更好。

图4 系统交流电流的d、q分量
图5分别为采用两种控制方案时,系统交流侧电流的总谐波失真(THD),采用改进控制方案的系统的THD为3.16,约为采用传统方案的系统的一半,系统静态性能得到明显提高。

图5 系统交流电流的THD
图6为采用改进控制方案的系统的有功电流和无功电流在其参考值分别于0.15 s发生跳变时的电流动态响应。电流能瞬间无超调跟踪新的参考值,说明采用改进控制方案的系统具有优良的电流动态性能。

图6 改进方案的系统交流电流动态响应
图7显示了电网a相电压在0.15 s发生20%跌落时有功和无功电流的波形。可以看出,无功电流仍旧保持为零,有功电流小范围抖动,即系统仍然以单位功率因数运行,只是电流幅值在小范围内变化,说明新控制方案对扰动具有补偿和抵抗能力。
4.2 实验结果分析
搭建了小功率实验样机进行验证,控制芯片为TMS320F28335,开关管选用 IKW40N60H3,交流电压有效值为50 V,其他实验参数与仿真一致,图8为实验波形。可以看到,整流器的输入电流、电压相位差接近零,输入电流正弦度好,达到了预期的控制目标,从而在实验上验证了提出的控制策略的正确性。
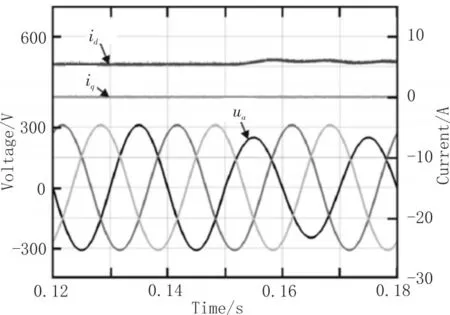
图7 电压不平衡时的id、iq波形

图8 输入相电流与相电压实验波形
5 结 论
该文针对传统等速趋近律电流滑模控制方案的鲁棒性和抖振之间的矛盾,引入扩张状态观测器对PWM整流器的扰动进行观测和补偿,并设计了新的滑模趋近律,在保证系统鲁棒性的同时抑制了电流抖振。仿真和实验结果表明,采用基于ESO和改进滑模趋近律控制方案的系统的静态性能优于传统滑模控制器,且动态响应快,抗扰动能力强,实现了系统的单位功率因数运行,输入电压电流均为正弦,验证了所提控制方案的有效性和优越性。

