初中数学深度教学重在触及本质、引领思维

贺玉亮

（福州第十五中学，福建福州 350009）

笔者在教学过程中发现，多数学生的思维处于低层次水平，体现在如认知肤浅缺乏深刻性、知识碎片化不成体系、思考无序导致思维混沌等问题。长此以往，极不利于学生逻辑思维的发展和整体认知的形成，极不利于学生形成系统的、深度的知识体系。

学生展开深度学习的前提是教师进行深度教学。但当前初中数学教学中，教师往往将公式推导过程简单理解为符号、形式的教学，不能把握编者的设计意图而忽视前后知识的关联，往往因过度关注计算结果而将解题过程解析化、几何化，忽略对解题思路的归纳和总结，从而降低了课堂教学的深度和品质，抑制了学生思维的发展。

因此，教师要静心研究教学，以实现初中数学深度教学，引导学生提升思考力、学习力。

一、精心设计预习梯度，引导学生由表及里思考

预习，指学生对即将要上的数学内容进行阅读。学生预习的目的，是初步了解其要点，做到心中有数，为上课做好必要的准备。由于数学教材结构严谨、逻辑性强，语言精练且抽象。教师通过精心设计有梯度的预习作业，兼顾不同层次学生，引导学生通过通读整体把握教材讲什么，通过精读弄清教材中的重难点，通过研读理清教材中公式（定理、性质等）的来龙去脉，促进学生良好的学习习惯养成，让学生学会由表及里思考。笔者以人教版初中数学教材七年级（上）1.2.4“绝对值”为例做说明。

1.通读——了解绝对值的定义

根据绝对值的定义填空:

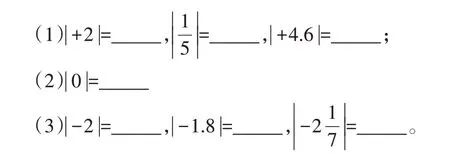
2.精读——厘清定义的表现形式，某个数的绝对值在数轴上是如何标识的，在解决有理数加减法运算中起到什么作用

（1）用三种语言（文字语言、符号语言、图形语言）表示绝对值的定义；

（3）绝对值等于4的数是_____；如果|x|=4，则x=_____。

3.研读——关于绝对值问题的相关重要题型及解决这类问题的基本方法

（1）若|x-2 |+|y-1 |=0，求x+y的值；

（2）若|x-1 |=1，求x的值_____。

设计意图：这份预习设计，阅读与练习相结合，由浅入深，内容的设计从特殊到一般（从数字到字母），既对学生有保底的要求，又对优生有拓展的要求，旨在引导学生弄清新旧知识之间的关联，激发学生发展高层次思维，引导深度学习。

二、巧妙设计变式教学，启发学生的数学思维由浅入深

数学领域里，变式无处不在。小至题目的图形、数字、条件、结论，大至教材、教法、考法，都存在变式。［1］数学变式教学，指教师设计系列问题对定理、公式、例题、习题等进行探索，通过“一式多变”“一法多变”“一题多解”“多解归一”等形式，引导学生在“变”的表象中探求“不变”的本质，并由“不变”的本质掌握数学规律、促进自身思维能力的提升。笔者以人教版八年级（上）13.3.1“等腰三角形”为例做说明。

问题：在图1中，已知BD=CE，∠ADB=∠AEC=90°，求证：AB=AC。

图1

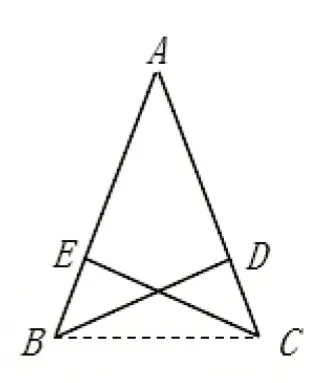
图2

变式1：以图1为基础，连接BC得图2。在图2中，已知在ΔABC中，BD、CE是⊿ABC的高，BD=CE。求证：AB=AC。

变式2：在图2中，已知在ΔABC中，AB=AC，BD、CE是ΔABC的高。求证：BD=CE。

变式3：在图2中，已知在ΔABC中，AB=AC，BD、CE是ΔABC的中线。求证：BD=CE。

变式4：在图2中，已知在ΔABC中，AB=AC，BD、CE是ΔABC的角平分线。求证：BD=CE。

变式5：在图2中，已知在ΔABC中，AB=AC，AE：AB=1：n，AD：AC=1：n。求证：BD=CE。

设计意图：教师设置变式2、3、4，意在引导学生探究出等腰三角形的新的性质，即等腰三角形两腰上的对应“三线”（对应高、中线、角平分线）相等；设置变式5，从特殊到一般，拓展到对应线段相等，意在引导学生爱好数学、学好数学，培养学生及时总结经验的习惯和概括问题的能力，从而发展学生的数学高阶思维能力。

三、精准进行课堂小结，带动学生的数学思维由窄变宽

学生掌握了数学规律，才能自如地运用知识，达到“遇难题迎刃而解”的状态。在设计课堂小结的过程中，教师一方面要对本课的知识要点进行归纳，完善学生知识体系；另一方面要关注本课知识与前后课知识之间的联系，实现知识结构一体化；再者要从思想方法层面对本课内容进行升华，拓展学生的数学思维。笔者以人教版八年级（下）第19章一次函数复习课“函数图象的变换”为例做说明。

本节课你有哪些收获？

1.知识构建

图3 “函数图像的变换”结构导图

2.知识拓展

图4 “函数图像的变换”思维导图

3.数学思想

数形结合，特殊到一般，分类，类比，模型思想。

设计意图：教师精准把握了该课的核心内容——一次函数的定义、图形、性质、应用，从知识构建、知识拓展和数学思想方法三个方面进行了小结，帮助学生梳理知识要点及蕴含的数学思想与方法，这样不仅可以帮助学生掌握知识与技能，而且能促进学生解题方法的优化、认知结构的形成、新知识模型的建立和思想方法的提炼，让学生的思维由单薄变得厚实。

四、优化设计课后作业，激发学生的数学思维由疏到密

课后作业是考查学生课程目标达成状况的重要方式，同时是课堂教学的延续。优化设计作业有助于全面考查学生的数学学业成绩，及时反馈教学效果，不断提升教学质量，促进学生的逻辑思维能力和创新思维能力的培养。［2］笔者以人教版八年级（上）14.2.2“完全平方公式”为例做说明。

1.运用完全平方公式计算

（1）(2x+3y)2；（2）(4x-5y)2；（3）(-3x-2y)2；

2.先化简，再求值：(a+2b)2-(2a-b)(2a+b)，其中a=2，b=-2.

3.要使4a2+ka+1成为完全平方式，则常数k的值为___________.

4.将多项式4x2+1加上一个单项式后，使其成为一个多项式的完全平方，请写出所有符合条件的单项式___________.

5.一个正方形的边长减少4cm，它的面积就减少64cm2，这个正方形的边长是多少？

6.已知x-y=5，xy=3，求x2+y2的值.

设计意图:第1、2题主要考查学生对完全平方公式结构特征的理解与运用；第3、4题为开放型题，主要考查学生对完全平方公式的综合应用，旨在培养学生的发散思维。第5题考查学生利用方程的思想建立数学模型，在化归思想的引领下运用完全平方公式进行运算。第6题主要考查学生对完全平方公式的拓展变形问题，帮助学生能够对公式中字母的指代对象、公式的结构特征及其相互区别达到透彻理解。另外，根据“问题引领学习”的原则，通过课后作业有效问题的设计，引导学生在解决问题的过程中，巩固所学的知识，提高数学思维能力，促进学生学业水平提升。笔者以某次学生的数学考试成绩为例做说明。（表1）

表1 实验班与非实验班入学、期末各项指标对比表

通过深度学习，达成了如下的教学效果：

1.引导学生构建知识体系。深度教学更加关注知识的整体性，把完整的知识系统地呈现给学生，让学生实现从量变到质变的飞跃。

2.学生的有效参与度明显提高。学生刚入学，学习兴趣高涨，回答问题也很积极，但多表现为答非所问。通过一段时间的深度教学，学生回答问题有一定的针对性，从肤浅的“热闹”转向深层次“思考”，从简单的模仿转向有目标的学习。

总之，深度教学将带给学生完整的数学体系和灵变的思维内涵，推进初中数学教学变革，促进数学核心素养培育落在实处。