双幅式梁桥挡风障阻风性能影响参数分析

林晓波，侯海涛，练江峰，胡 磊，卓卫东，林 立

(1. 福州大学土木工程学院，福建 福州 350108； 2. 福建省风灾害与风工程重点实验室，福建 厦门 361024； 3. 厦门市公路事业发展中心，福建 厦门 361000； 4. 厦门中平公路勘察设计院有限公司，福建 厦门 361000； 5. 厦门理工学院土木工程与建筑学院，福建 厦门 361024)

0 引言

中国东南沿海等地区受大风，甚至台风影响显著[1-3]，使得地区桥梁桥面横风较大，不利于桥面行车安全[4]，而设置挡风障是保障桥面车辆在大风天气顺利通行最有效的手段之一[5]. 目前，许多学者研究了桥梁挡风障高度、 孔隙率等参数对单幅式桥梁挡风障桥面阻风性能规律及行驶车辆安全性的影响[6-8]，但大多数研究是针对规范的障条式挡风障，未系统比较其他型式挡风障的阻风性能，未量化评价各结构参数与阻风效率的相关性. 与此同时，公路桥梁车道随国内汽车保有量的增加而增加，桥面宽度持续变大[9]，由于桥梁外观、 结构受力等因素制约桥梁建造的宽度[10]，西堠门大桥[11]、 泉州海湾桥[12]、 甘溪特大桥[13]等许多桥梁采用双幅式桥面. 该类型桥梁与单幅桥梁有较大不同，其桥上行车安全能力是否对挡风障安装片数、 来流条件等要素敏感？对挡风障阻风性能的影响规律如何？均有待具体分析和试验验证. 同时，鉴于试验参数较多，且风洞试验费用昂贵，本次研究主要采用正交试验，以减少试验工作量，提高研究效率[14-15]. 基于正交试验，开展某跨海双幅式箱梁模型的挡风障参数测速试验，分析挡风障安装片数、 来流风偏角、 来流风速、 圆孔组合方式等参数对双幅式桥梁挡风障阻风性能影响程度.

1 风洞试验方法及试验方案

1.1 试验影响因素

图1 桥梁搭载平台模型 Fig.1 Bridge platform model for carrying wind barriers

针对双幅式梁桥挡风障安装片数、 来流风偏角、 来流风速、 圆孔组合方式等阻风性能影响因素进行试验研究，并考虑安装片数分别与风偏角及来流风速的交互作用，且每种因素选择2个水平进行研究.

1.2 搭载平台及挡风障模型

搭载平台桥梁为某实际双幅式桥梁缩尺模型，如图1所示. 该桥梁模型长3.075 m，外壳采用3 mm的ABS板，芯梁及中隔板使用钢材，以保证模型刚度.

为研究圆孔组合方式等参数对挡风障阻风性能的影响，设计并制作了高度为15 cm拼接与渐变圆孔挡风障模型，障板采用与工程应用相近的PC耐力板制作. 各方案参数如表1所示, 模型如图2所示.

表1 挡风障方案参数表

图2 挡风障模型Fig.2 Wind barrier models

将挡风障安装于该桥梁缩尺模型上，探究安装片数对双幅式桥梁挡风障阻风性能影响程度，模型几何缩尺比的选择考虑了阻塞比的影响，阻塞比ζ[16]的计算式为：

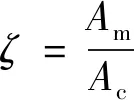
(1)

式中：Ac为风洞试验段的横截面积(m2)；Am为试验模型在试验段横截面的最大投影面积(m2).

最终选择搭载平台桥梁和挡风障模型缩尺比为1∶20，阻塞率为4.5%，满足试验要求.

1.3 桥位区域风场及试验工况

为了研究来流风速(uo)、 风偏角对挡风障阻风性能产生的影响，风速取值考虑了桥址实桥设计基准风速60.59 m·s-1(百年一遇). 统计并分析了某实际双幅式梁桥桥面实测风数据，绘制风玫瑰图如图3所示，桥面风速主风向与桥梁中轴线夹角为112°； 受“莫兰蒂”台风影响，桥面极值风速为42.1 m·s-1，鉴于台风风向随机性，该风速下风偏角取为较不利的90°.

图3 某双幅式桥梁桥位区风玫瑰图Fig.3 Wind rose of a twin parallel deck bridges location

综合试验模型及区域风场工况分析的结果，汇总试验影响因素及水平如表2所示.

表2 试验影响因素与水平汇总表

2 风洞试验条件及测点布置

试验主要设备为眼镜蛇三维脉动风速测量仪，采集频率为0～2 kHz，采集风速范围为2～100 m·s-1. 在实际使用中发现当眼镜蛇采样频率过大，其存在一定误差，故本次试验中，设置眼镜蛇测风仪采样频率为600 Hz，各测点采样时长为60 s.

考虑到公路桥梁通常对桥面车辆限制通行高度为5 m，故本次试验主要测量裸桥和安装不同桥梁挡风障方案之后，箱梁跨中中间行车道中心处0～250 mm高度范围内的风速分布情况. 测点从2.5 cm高度开始设置，每隔2.5 cm设置一个，每个车道共10个风速测量点，测点布置如图4所示.

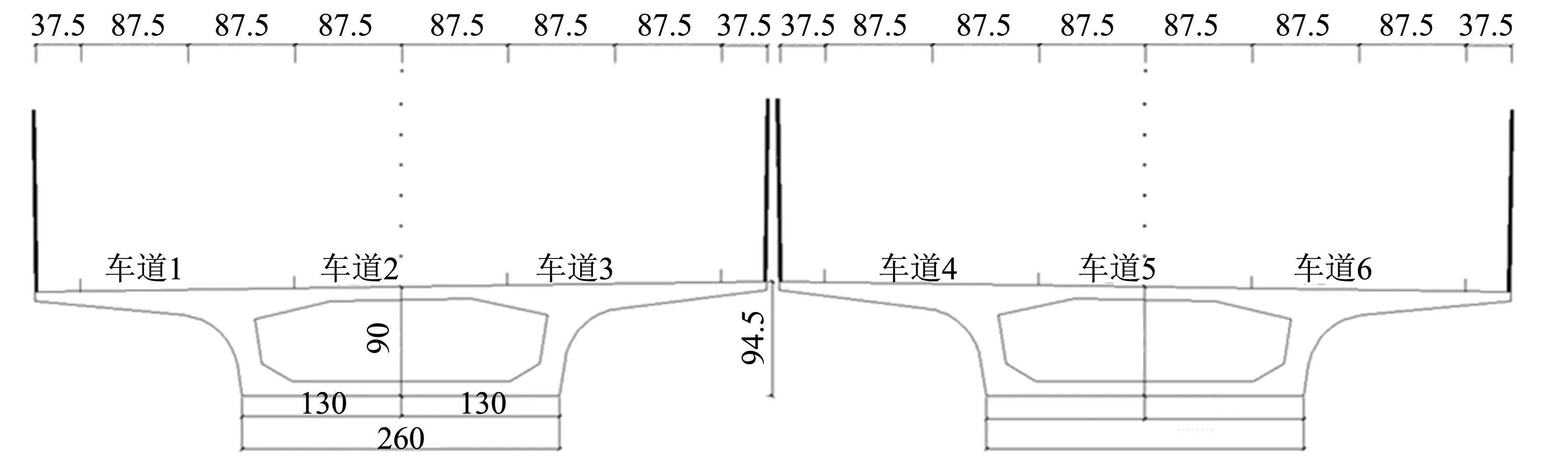
图4 风速测点分布图(单位：mm)Fig.4 Distribution of wind speed measurement points (unit: mm)

试验中，同时架设3台眼镜蛇三维脉动测风仪，其中1台用来监测来流风速，其余2台眼镜蛇三维脉动测风仪作为测量设备安装于定制的支架上并与移侧架连接，用来测量桥面各车道中心线一定高度范围内的平均风速剖面图，眼镜蛇布置场景如图5所示. 在正式试验开始前，宜对测风仪进行位置校准. 通过风洞移侧架，将测量测点风速的测风仪移至桥梁模型前迎风端，以减少或避免桥梁模型对测得来流风向的干扰，并在5 m·s-1均匀来流风速条件下，对3台测风仪的俯仰角、 偏航角进行校准，使两个角度尽可能接近0°，以确保测风仪安装位置准确.

图5 试验模型及测风仪布置示意图Fig.5 Test models and layout of anemometers

3 风洞试验结果分析

3.1 平均风速折减系数剖面图

试验结束时，将各测点风速除以来流风速，得到各测点平均风速折减系数(r). 将各测点的风速折减系数沿高度方向连成线，可得到的各车道中心线上方0～250 mm高度范围内的平均风速折减系数剖面图. 其中，2片、 4片工况平均风速折减系数剖面对比图如图6, 图7所示.

由图6、 图7可知：

1) 桥梁挡风障对其结构高度范围附近测点的遮挡效果较好，而对迎风侧车道200 mm高度以上测点的遮挡效果较差，甚至出现了风速折减系数大于1的现象. 这是由于设置挡风障，让裸桥工况下从桥面通过的气流更多以绕流形式从挡风障结构顶部通过结构物并与来流风速叠加，使得挡风障顶部风压大于裸桥工况，因而风速较大. 同时，随着车道距迎风侧挡风障距离的增加，绕流与来流的叠加效应逐渐减弱，因此，靠近背风侧车道在相同位置处测点风速小于靠近迎风侧车道.

2) 2片工况在靠近迎风侧车道测点平均风速折减系数与4片工况接近，而在靠近背风侧车道上，4片工况各测点平均风速折减系数明显小于2片工况. 这是由于箱梁迎风面对来流的阻挡作用使得箱梁底部及附近区域风压较大，而双幅式桥梁中间孔隙处风压较低，故有气流从箱梁底部从流向背风一侧桥面，并对中间无遮挡作用的2片工况产生较大影响，平均风速折减系数较大，而4片影响较小，故其靠近背风侧车道平均风速折减系数较小.

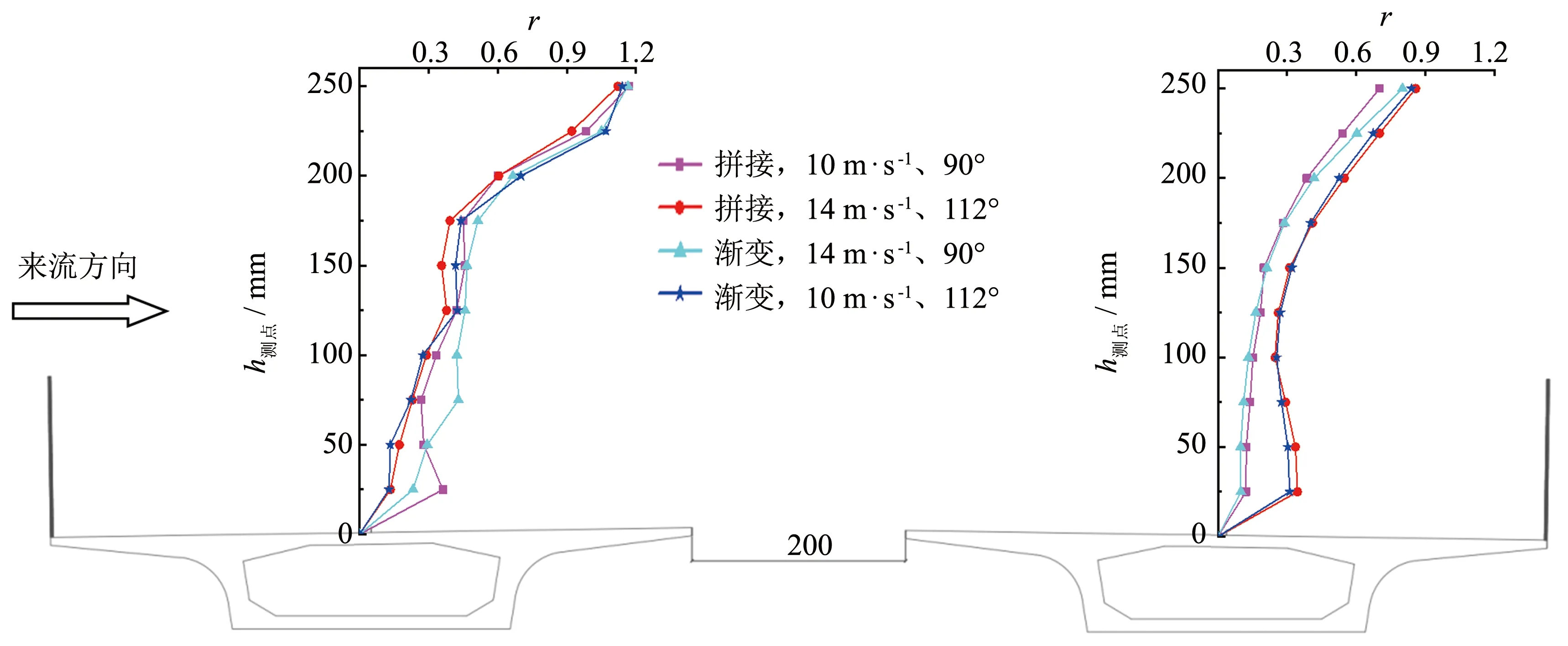
图6 两片工况平均风速折减系数剖面对比图Fig.6 Comparison of the average wind speed reduction coefficient profile under 2 pieces barriers conditions

图7 四片工况平均风速折减系数剖面对比图Fig.7 Comparison of the average wind speed reduction coefficient profile under 4 pieces barriers conditions

3.2 不同车道阻风效果

图8 车道风速折减系数汇总图Fig.8 Wind speed reduction coefficients for each lane

为了更直观分析各参数对双幅式桥梁挡风障阻风性能的影响，以基于风剖面压力等效原则计算得到的桥面等效风速折减系数[17]为指标进行结果分析，各车道的风速折减系数的计算式为：

(2)

式中：Zr为桥梁风剖面高度，取25 cm；u(z)为车道在Z高度处的横向风速值.

为分析各工况下，挡风障在不同车道上的阻风效果，将各车道风速折减系数绘制于图8.

由图8可知，8个试验工况得到车道2、 车道5风速折减系数图形规律一致，在10 m·s-1、 112°来流条件下，4片渐变挡风障在车道2、 车道5上测得的风速折减系数最低，分别为0.54、 0.17，这说明该方案挡风效果最好. 其次，迎风侧车道风速折减系数大于靠近背风侧车道，这趋势随着方案挡风性能增加而凸显，6号试验两车道风速折减系数差值最大，达到0.37. 这说明，挡风障需要距离车辆有一定距离，才能实现高效遮挡. 因此，设置挡风障时，需要使其距离迎风侧车道一定距离，以保障迎风侧车道上行驶车辆的安全性. 实验工况及结果汇总于表3.

表3 试验结果分析

3.3 正交试验结果分析

3.3.1正交试验结果直观分析

试验结果直观分析表如表4所示. 其中，Kij表示因素j所在列中所有水平的数据之和，i=1, 2；j=A, A*C, B, C, A*D, D；Rj为因素j两水平的极差.

表4 试验结果直观分析

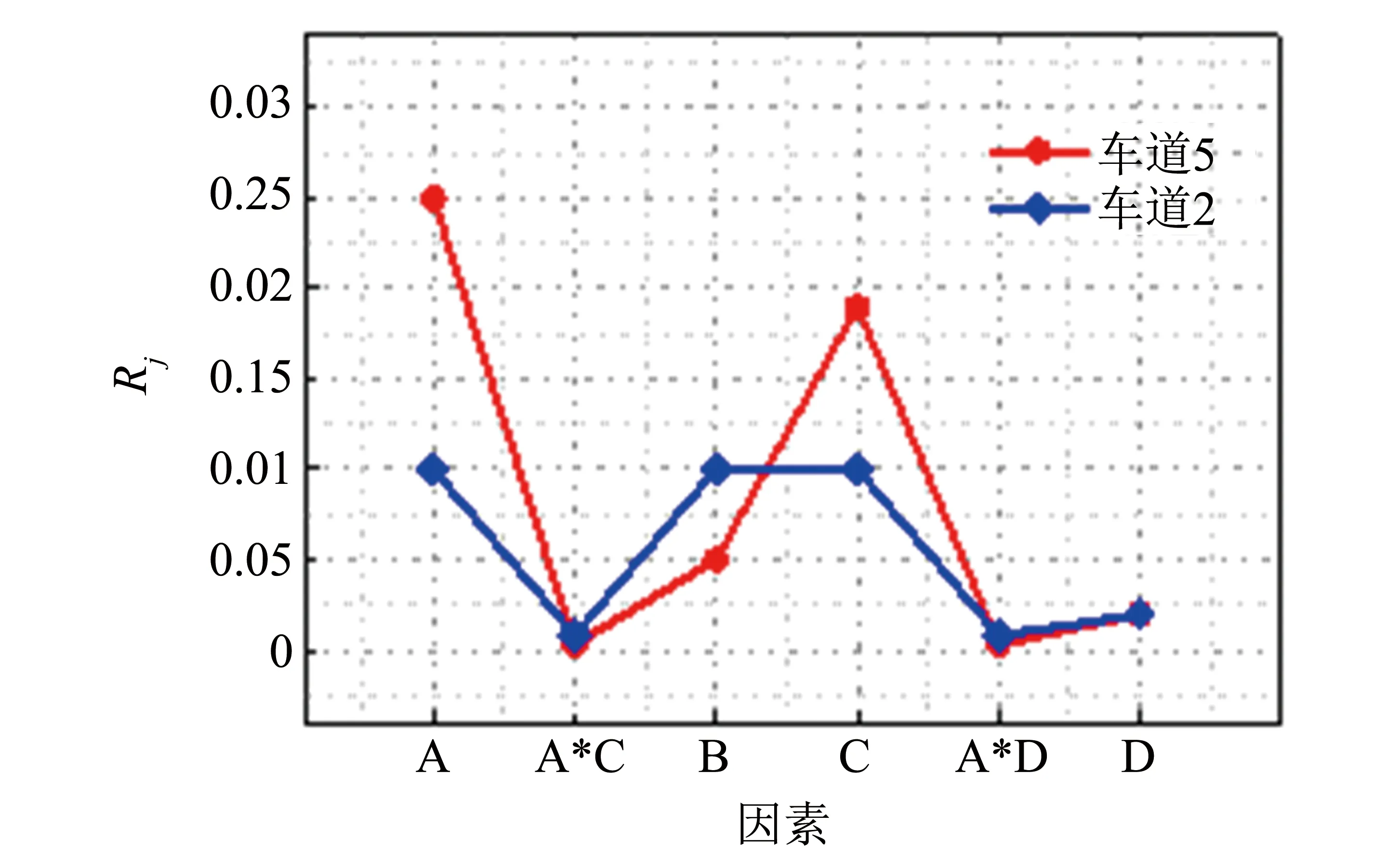
图9 不同因素车道风速折减系数极差对比Fig.9 Comparison of wind speed reduction coefficients for each lane under different parameters

由表4可见，车道风速折减系数极差Rj越大，说明该因素对车道风速折减系数影响越大，是挡风障阻风性能的重要影响因素.

为了直观对比不同因素车道风速折减系数极差，将不同车道风速折减系数Rj绘制于图9. 由图9可知，双幅式桥梁挡风障桥面等效风速折减系数各影响因素重要性在不同车道上除了风速均为重要性最低以外，其他因素具有一定差异性. 综合考虑，各因素影响程度由高到低依次为：安装片数、 来流风偏角、 圆孔组合方式和来流风速. 安装片数与风偏角及来流风速交互作用不明显.

3.3.2正交试验的方差分析

直观分析主要对不同因素进行重要性排序，为了估计试验误差，判断各因素对试验指标影响的显著程度，采用方差分析法进一步分析. 由试验结果计算得到不同因素影响下，各车道方差如表5所示. 其中，Sj表示因素j偏差平方和，j=A, A*C, B, C, A*D, D；Se为空白列随机误差引起的偏差平方和. 由于交互作用列误差小于随机误差，故将两列方差及自由度并入随机误差中，即最终随机误差引起的偏差平方和之和Se*=SA*C+SA*D+Se，故车道2与车道5的Se*分别为2.49×10-5、 4.65×10-5.

表5 车道2、 车道5不同因素偏差平方和汇总表

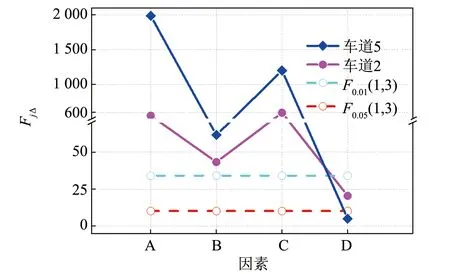
图10 不同因素下车道F检验折线图Fig.10 F-test values of each lane under different parameters

为分析各因素对挡风障阻风性能的影响程度，计算各因素下的F值，并绘制于图10. 其中，FjΔ表示因素j的F值；F0.05、F0.01表示显著性水平分别为0.05、 0.01的F检验临界值. 当某因素FjΔ>F0.01时，表明该因素水平的改变对双幅式桥梁这一车道风速折减系数有显著影响的可信度为99%，即该因素对这一车道风速折减系数影响是高度显著的； 当某因素FjΔ>F0.05时，表明该因素水平的改变对双幅式桥梁这一车道风速折减系数有显著影响的可信度为95%，即该因素对这车道风速折减系数影响是显著的； 否则，该因素对这车道风速折减系数无显著影响.

由图10可知：

1) 因素A、 B、 C对车道2、 车道5等效风速折减系数影响是高度显著的，即上述三种因素对挡风障阻风性能影响是非常显著的. 因素D对车道2等效风速折减系数影响是显著的，但对车道5等效风速折减系数无显著影响.

2) 不同因素对双幅式梁桥挡风障不同车道阻风性能影响程度具有差异性，车道2上各因素影响程度由高到低依次为：C、 A、 B、 D； 车道5上各因素影响程度由高到低依次为：A、 C、 B、 D.

4 结语

以某跨海双幅式梁式桥为工程背景，开展风洞测速试验，分析了各方案后方车道的平均风速折减系数剖面图; 以车道风速折减系数为阻风性能评价指标，采用正交试验方法，研究了挡风障安装片数、 来流风偏角、 来流风速、 圆孔组合方式等参数对双幅式桥梁挡风障阻风性能的影响, 得到以下主要结论：

1) 迎风侧车道风速折减系数大于靠近背风侧车道，这趋势随着方案阻风性能增加而凸显，6号试验挡风效果最好，两车道风速折减系数差值最大，达到0.37.

2) 挡风障安装片数、 来流风偏角、 圆孔组合方式对挡风障阻风性能影响是非常显著的，来流风速对车道2等效风速折减系数影响是显著的，对车道5等效风速折减系数无显著影响.

3) 不同因素对挡风障在不同车道的阻风性能影响程度具有差异性，车道2上各因素影响程度由高到低依次为：圆孔组合方式、 安装片数、 来流风偏角、 来流风速； 车道5上各因素影响程度由高到低依次为：挡风障安装片数、 圆孔组合方式、 来流风偏角、 来流风速.

4) 安装片数对双幅式桥梁靠近迎风侧车道桥面风场影响较小，而对靠近背风侧车道影响较大，且其与来流风偏角及风速的交互作用不明显.

综上所述，对于双幅式桥梁挡风障选型时，需要着重考虑挡风障安装片数、 圆孔组合方式及距离迎风面车道位置，此外，在开展双幅式桥梁挡风障阻风性能试验时，可不设置多种风速工况，但应结合当地或者实桥桥面测得风速数据，开展多种风偏角来流工况下挡风障阻风性能测试.