基于贝叶斯网络的大学生共享单车出行行为研究

刘诗序，唐颖诺，王智煜，贺朝阳

(1. 福州大学土木工程学院，福建 福州 350108; 2. 国家知识产权局专利局专利审查协作北京中心福建分中心，福建 福州 350100)

0 引言

近年来，共享单车发展迅速，与其他出行方式相比，共享单车出行利用手机应用扫码解锁，且可以随停随放，使用灵活，具有明显的独特性，已经成为人们日常出行的重要方式，因此，对共享单车出行行为进行研究具有实际意义.

国内外有关出行行为的研究大多采用非集计模型. 例如，文献[1]基于分层Logit模型，研究居民日常出行方式选择行为； 文献[2]利用分层Logit模型对居民短途出行行为进行研究. 基于Logit模型的出行行为研究着重于分析不同因素对出行行为的影响，并且认为各影响因素相互独立，但实际上出行选择往往是多个因素相互作用的结果，因此，有必要对不同因素相互作用下的居民出行行为进行分析和预测. 而贝叶斯网络在分析各因素对出行方式选择的影响的同时，也考虑了各因素之间的相互影响，且近年来在交通领域逐渐受到关注. 如：文献[3]使用贝叶斯估计方法来估计网络的参数，并建立贝叶斯网络模型来反映公共自行车出行选择行为与其他主要因素的交互作用； 文献[4]基于贝叶斯网络模型对出行链进行研究，利用软件编程对模型进行求解，得到出行链的预测模型.

共享单车出现时间短，相关研究相对较少. 文献[5]利用多项Logit模型对北京的共享单车选择影响因素进行分析； 文献[6]运用混合嵌套大型邻域搜索和可变邻域下降算法，对自行车再平衡问题进行研究. 综上可知，对共享单车出行行为研究仍主要采用传统的Logit模型，考虑到共享单车影响因素之间的相互作用，本文采用贝叶斯网络方法研究共享单车出行行为，以大学生群体为研究对象，建立大学生共享单车出行行为分析的贝叶斯网络模型，对影响大学生共享单车出行行为的因素进行分析.

1 贝叶斯网络模型构建

贝叶斯网络是一个概率-图模型，用于描述变量之间的相互关系. 网络中每个节点表示相应变量，任意节点之间若有边连接，则表示该节点之间存在依赖关系，通常由父节点指向子节点[7]. 贝叶斯网络可以通过贝叶斯网络学习得到，贝叶斯网络学习的目的是构建一个与样本集最一致的网络结构，包括结构学习和参数学习两个部分.

1.1 建模数据

将大学生共享单车出行分为校内出行与校外出行，通过总结共享单车出行行为相关研究成果，筛选得到模型节点变量12个，以此作为问卷设计依据. 以福州市大学城各高校学生为调查对象，采用随机抽样调查的方法，共发放600份问卷，回收有效问卷577份. 其中，男生占52%，女生占48%； 拥有私人交通工具的学生占37.6%，没有私人交通工具的学生占62.4%. 各节点变量定义及取值如表1所示.

表1 贝叶斯网络节点变量定义及取值

1.2 贝叶斯网络结构学习

贝叶斯网络结构学习的主要目的是结合先验信息，通过分析样本数据集得到各节点之间的相互关系，并建立相应的网络结构，使其与样本数据集相吻合. 本研究采用基于搜索评分的方法[8]，以贝叶斯评分函数作为评分准则，并基于K2算法[7]进行结构搜索，从而完成贝叶斯网络结构学习. 具体步骤如下：

1)互信息值计算. 对于节点Xi和Xj，其互信息[9]MI(Xi,Xj)计算公式如下：

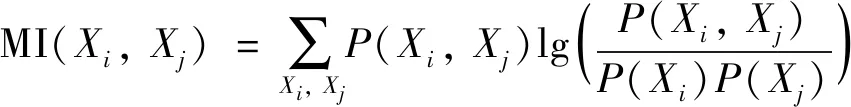
(1)

根据该计算公式，基于所得出行数据利用MATLAB软件运算得到各节点的互信息值, 如表2所示.

表2 出行方式选择与变量间的互信息值

2)确定节点初始排序. 基于互信息值确定各影响因素与决策变量(出行方式)之间的关联性大小，从而给定初始变量次序为GE、 GR、 IN、 CO、AP、 DI、 HA、 PE.

3)网络构建. 从一个空白网络开始，基于给定的评分函数，按照节点次序依次历遍每个节点，选择后验概率值最大的作为该节点的父节点，并用有向边连接，逐步完成网络的构建. 评分函数如下[7]：

(2)

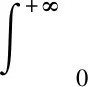
基于MATLAB中的BNT工具箱完成上述步骤，贝叶斯网络学习结果如图1～2所示.

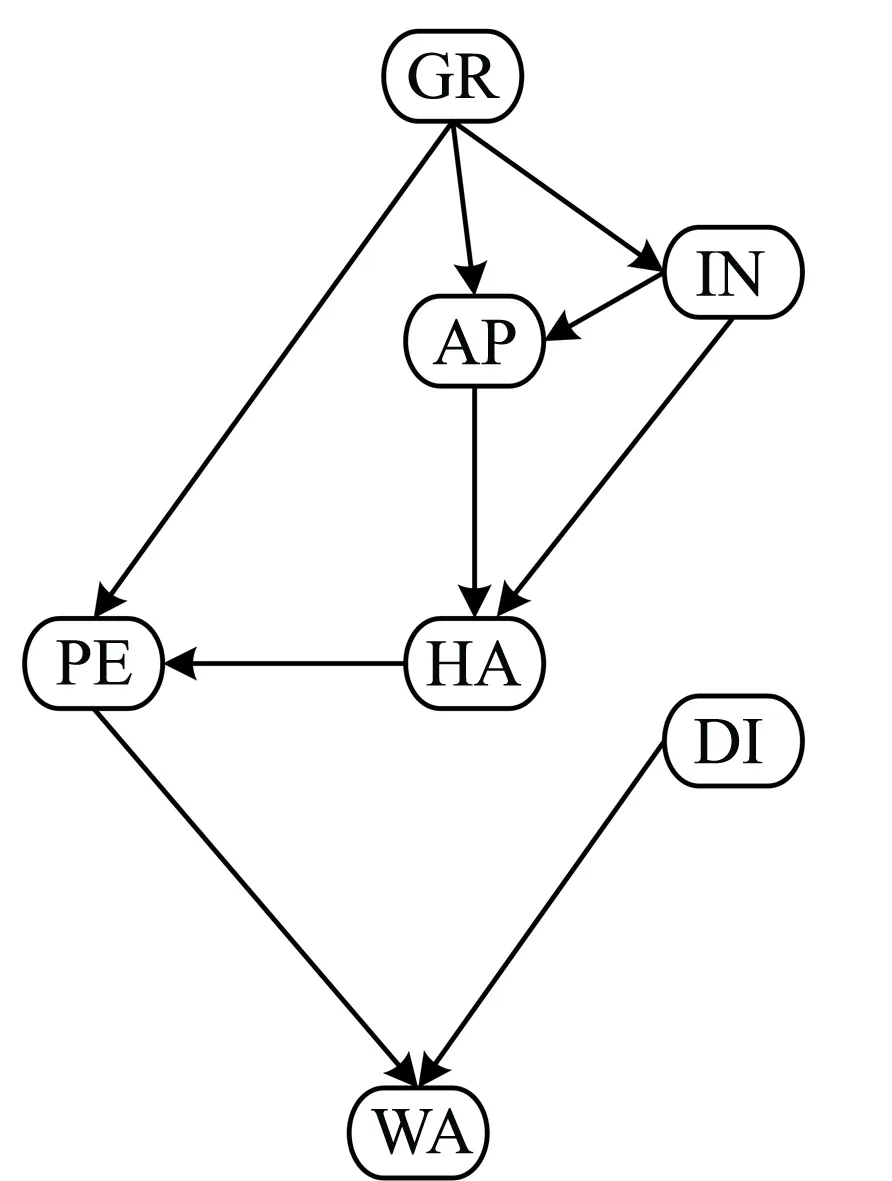
图1 校内出行贝叶斯网络结构Fig.1 Bayesian network structure for campus travel

图2 校外出行贝叶斯网络结构Fig.2 Bayesian network structure for off-campus travel

通过所获得的贝叶斯网络结构可以对变量间的相互关系进行直观的描述，若节点之间存在有向弧，则节点之间存在依赖关系，如图1中节点GR与节点AP存在有向弧连接，表示节点AP的取值均会受到节点GR状态值的影响. 因此，由图1可知，DI和PE对WA(校内)产生直接影响，而GR、 IN、 HA、 AP等则对WA(校内)产生间接影响； 由图2可知，DI和PE对WA(校外)产生直接影响，而GR、 IN、 HA、 CO、 AP等则对WA(校外)产生间接影响.

1.3 贝叶斯网络参数学习

贝叶斯网络的参数学习是指基于给定的网络结构，对样本数据集进行学习，获得各节点的概率分布的过程. 为了充分考虑先验信息对估计结果的影响，本研究采用贝叶斯估计方法确定贝叶斯网络参数. 假设贝叶斯网络参数θ的先验分布P(θ)服从Dirichlet分布，即：

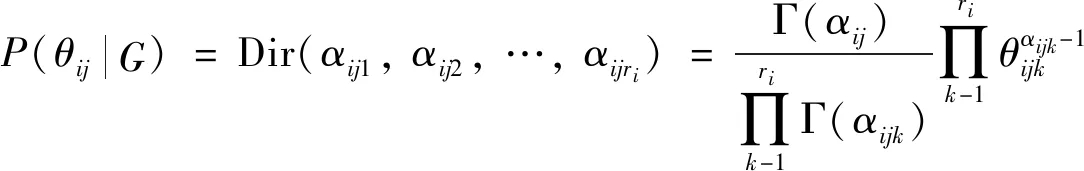
(3)

由于Dirichlet分布为共轭分布，故参数θ的后验分布也为Dirichlet分布，即：

=Dir(αij1+nij1,αij2+nij2, …,αijri+nijri)

(4)

则参数θ的后验估计为：

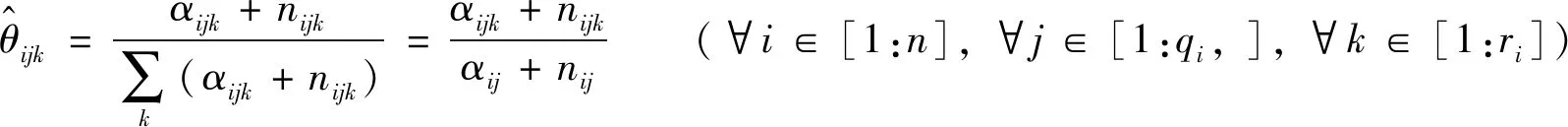
(5)

利用MATLAB得到参数学习结果，以表3为例，表中数据表示该节点的后验概率.

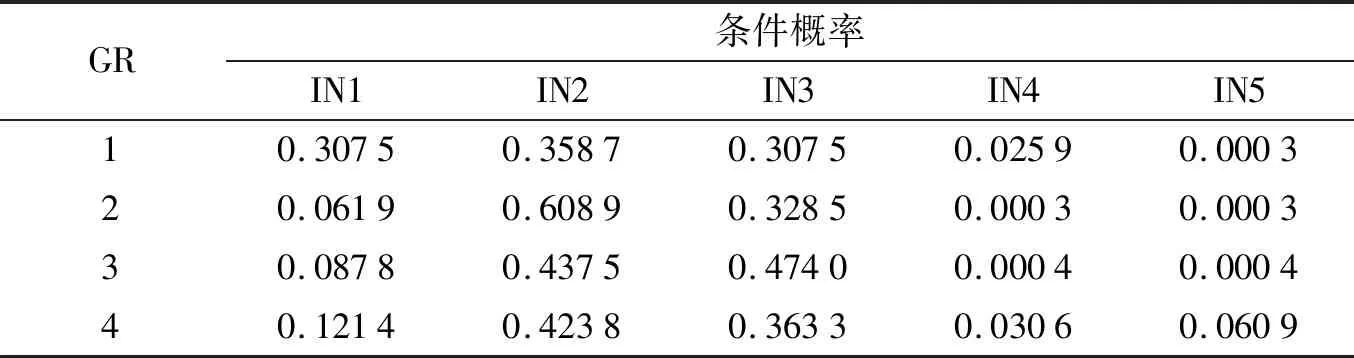
表3 节点GR参数估计表

1.4 模型有效性验证

以校外出行为例验证模型有效性，将贝叶斯网络学习结果与样本数据进行对比，结果如表4所示. 从表4可以看出，选择共享单车出行的概率的实际值与学习值的最大绝对误差值为0.017，平均绝对误差值为0.000 7，最大相对误差为0.378，平均相对误差为0.009 8. 其中最大相对误差较大是因为所得到的样本数据中该类样本量过少，但总体来看，学习精度较高，说明该模型适用性较好. 此外，使用Logit模型进行预测时，最大绝对误差为0.157 0，平均绝对误差为0.040 5，最大相对误差为0.886 7，平均相对误差为0.186 2. 由此可见，与Logit模型预测结果相比，贝叶斯网络模型学习结果的误差更小，在分析共享单车出行行为影响因素时更有效.

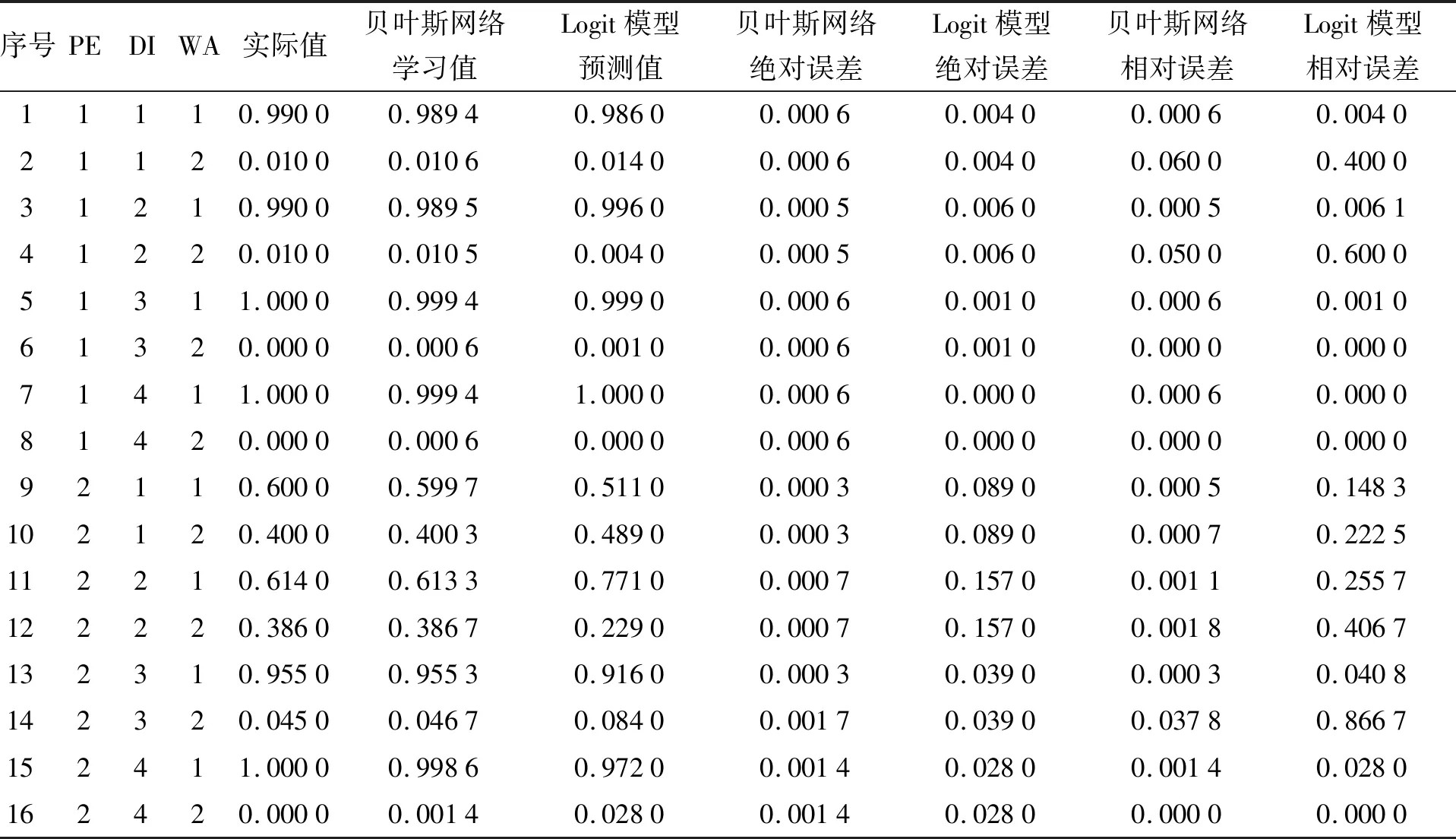
表4 条件概率对比结果

2 共享单车出行影响因素分析

推理分析是贝叶斯网络模型的一项主要功能，本研究基于这一功能，分析各因素对使用共享单车出行的影响.

2.1 贝叶斯网络推理基本理论

利用联合树算法进行推理[7]，以共享单车校内出行为例，其主要步骤如下：

步骤1贝叶斯网络转化为道义图. 将所构建的贝叶斯网络中的有向边改为无向边，从而将有向图(图1)转化为无向图，然后将拥有相同子节点的各父节点连接起来，所得到的新的结构图称之为道义图，如图3(a)所示.

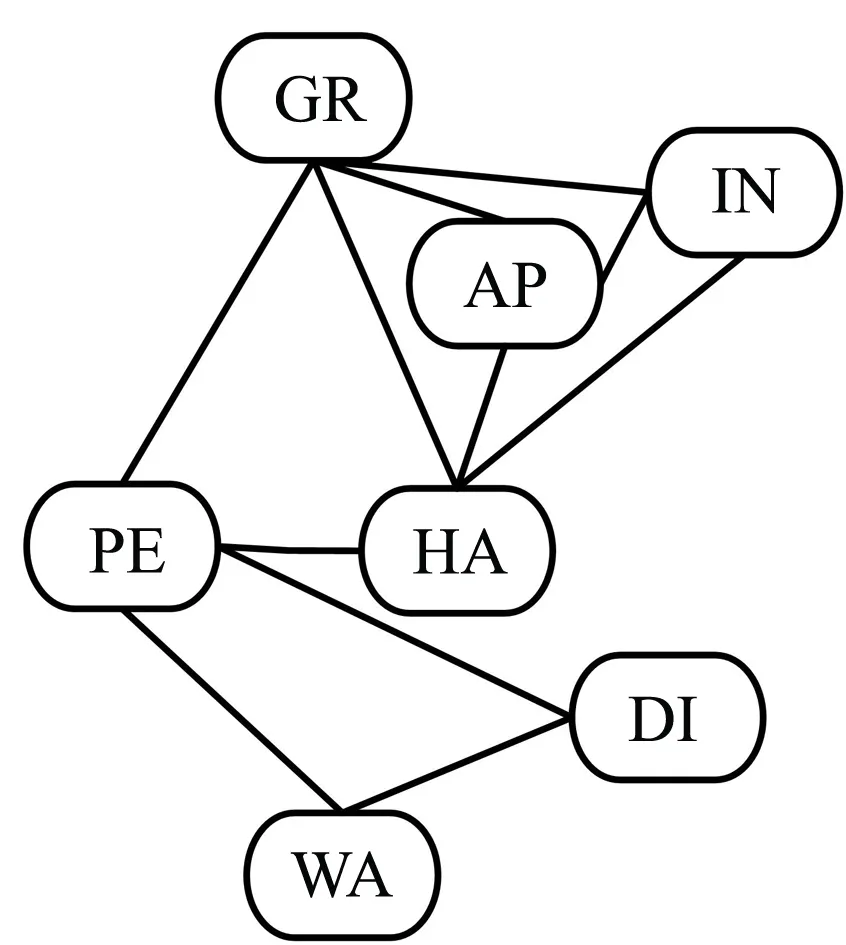
步骤2道义图三角化. 三角化是指在道义图的基础上通过增加边的方式破除超过三个节点的环，得到三角化图，如图3(b)所示.

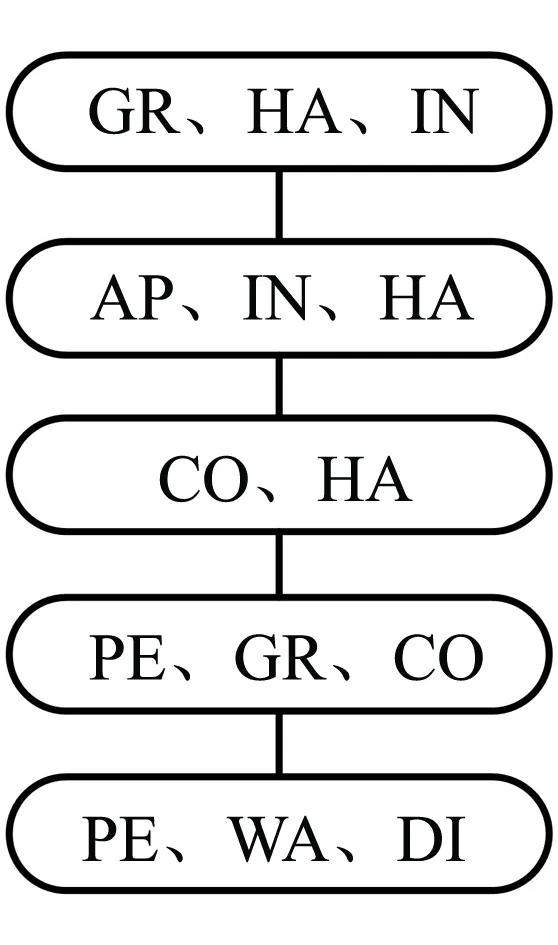
步骤3联合树生成. 三角化图中若某完全子图不被其他子图包括在内，则被称为极大完全子图，该极大完全子图又称为团节点，将团节点组织起来，即形成联合树T，如图3(c)所示，同理可得校外出行贝叶斯网络的联合树，如图3(d)所示.

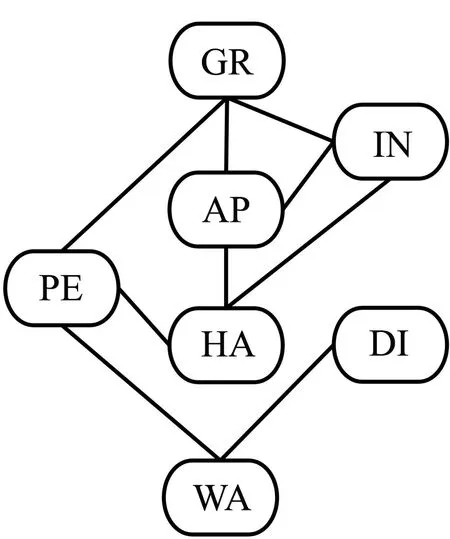
(a) 道义图(校内)

(b) 三角化图(校内)

(c) 联合树(校内)

(d)联合树(校外)

步骤4联合树的消息传播. 已知贝叶斯网络结构中各节点的条件概率，可根据已知某些节点的取值E=e，将包含所需查询的变量的团节点作为传递信息的枢纽，从而根据下式计算得到该变量的后验概率P(Q|E=e).

(6)

2.2 影响因素推理分析

本研究基于MATLAB的BNT工具箱中的联合树推理模型，分析各因素对共享单车出行的影响.

Ⅰ) 不同年级(GR)对出行方式的影响. 由表5可知，不同年级对校内出行与校外出行均有影响，但影响大小不同，且从总体上来看，校外出行中各年级选择共享单车的概率比校内出行小.

表5 年级对共享单车出行的影响

Ⅱ) 是否拥有私人交通工具(PE)对出行方式的影响. 由表6可知，是否拥有私人交通工具对校内出行与校外出行均有影响，拥有私人交通工具时，选择共享单车出行的概率更小，且校内出行与校外出行选择共享单车出行的概率差别不大，但是，若没有私人交通工具，校外出行选择共享单车出行的概率小于校内出行.

表6 私人交通工具对共享单车出行的影响

Ⅲ) 每月生活费(IN)对出行方式的影响. 由表7可知，每月生活费对校内出行与校外出行均有影响，但影响大小不同，总体来看，不同取值状态下校外出行选择共享单车出行的概率比校内出行更小.

表7 每月生活费对共享单车出行的影响

表8 使用意愿对共享单车出行的影响

Ⅳ) 使用意愿(AP)对出行方式的影响. 由表8可知，使用共享单车的意愿越高，实际选择共享单车出行的概率就越高，但概率相差不大，因为使用意愿对是否选择共享单车出行不产生直接影响，而是通过影响出行习惯产生间接影响. 此外，与校内出行相比，校外出行中选择共享单车出行的意愿更低.

Ⅴ) 交通费用(CO)对出行方式的影响. 由表9可知，当出行费用在1～2元时，选择共享单车的出行概率明显低于其他费用水平下的概率，这是因为1～2元是乘坐普通公交的费用，在该费用水平学生一般会选择公交出行.

表9 交通费用对共享单车出行的影响(校外)

Ⅵ) 出行习惯(HA)对出行方式的影响. 由表10～11可知，出行习惯对校外出行与校内出行均有一定影响，与校内出行相比，校外出行中，选择共享单车出行和步行的概率有所下降.

表10 出行习惯对共享单车出行的影响(校内)

表11 出行习惯对共享单车出行的影响(校外)

Ⅶ) 出行距离(DI)对出行方式的影响. 由表12可知，对于校内出行，随着出行距离的变化，选择共享单车出行的概率也相应发生变化，由此可见出行距离对于是否选择共享单车出行有一定影响； 对于校外出行，当出行距离在1 km以内及1～3 km时，选择使用共享单车的概率均在21%左右，随着出行距离的增加，选择共享单车出行的概率大幅下降. 这是因为，当距离较远时，出于出行时间和体力消耗的考虑，选择共享单车出行的概率会降低，由此可见，出行距离对于是否选择共享单车出行具有较为显著的影响. 出行距离对校内出行与校外出行均有影响，但由于校内出行大多在2 km以内，与校外出行相比，校内出行对于出行距离的敏感程度有所不同.

表12 出行距离对共享单车出行的影响

3 结论

1) 对于校内出行，共有6个因素对大学生出行方式产生影响，其中直接影响因素有：出行距离和是否拥有私人交通工具； 间接影响因素有：年级、 每月生活费、 共享单车使用意愿和出行偏好. 与校内出行相比，校外出行增加了一个交通费用间接影响因素(其他影响因素相同).

2) 贝叶斯网络学习结果的误差值较小，学习精度较高； 与Logit模型预测结果相比，贝叶斯网络模型的学习结果误差值更小，说明本研究模型更为有效.

3) 基于贝叶斯网络的推理功能，将校内与校外出行进行对比，结果显示, 年级、 出行距离以及是否拥有私人交通工具等对校内出行和校外出行的影响程度有所不同.