截面形式对R-UHPC梁抗弯承载力的影响

马熙伦，杨 简，陈宝春，林上顺

(1. 宁夏大学土木与水利工程学院，宁夏 银川 750021； 2. 福州大学土木工程学院，福建 福州 350108;3. 福建工程学院土木工程学院，福建 福州 350118)

0 引言

超高性能混凝土(ultra high performance concrete, UHPC)的抗拉能力虽然较之普通混凝土高，但在抗弯结构中仍然需要钢筋或预应力筋来承受拉应力[1-2]. 在钢筋超高性能混凝土(R-UHPC)梁抗弯承载力计算时，现有相关标准有的考虑UHPC的抗拉贡献[3-4]，有的则没有[5]，认为它的贡献很小[6].

文献[7]开展了具有不同钢纤维掺量的R-UHPC矩形梁抗弯性能试验与计算分析，认为当梁中的UHPC无假性应变硬化时，可以不考虑UHPC抗拉强度对梁抗弯承载力的贡献，而当有硬化段时, 特别是当UHPC的抗拉极限应变超过钢筋屈服应变时，UHPC抗拉贡献率大于20%，应予考虑. 换言之，在R-UHPC梁抗弯承载力计算时，是否考虑UHPC的抗拉贡献，要根据UHPC本身的抗拉性能来定.

在实际工程应用中，混凝土梁常用的截面形式有矩形、 箱形和T形. 文献[7]研究的对象是矩形梁，文献[5-6]的结论则是基于文献[8]的T形梁试验结果. 本文作者认为梁截面形式对UHPC抗拉强度在R-UHPC梁抗弯承载力的贡献也有影响，而目前未见相关的研究.

为此，本研究在文献[7]的基础上，以截面形式与UHPC中的纤维掺量为参数，通过实测获得7种不同纤维掺量UHPC的抗拉和抗压等材性，对矩形、 箱形和T形R-UHPC梁的承载力进行计算分析，以明确截面形式对UHPC抗拉强度在R-UHPC梁抗弯承载力贡献的影响，并依此给出相应的设计计算建议.

1 R-UHPC梁材性与截面形式

1.1 UHPC材性

UHPC拉伸性能主要受基体与纤维增强效应的影响. 采用同一基体，设计钢纤维掺量分别为0、 0.5%、 1.0%、 1.5%、 2.0%、 2.5%和3.0%的7种UHPC. 钢纤维均采用长13 mm、 直径0.2 mm的微细圆直形钢纤维(简称纤维). 基体配比(水胶质量比采用0.18)、 制备方法和养护制度与文献[9]相同.

单轴拉伸试验采用文献[10]的试验方法，抗压强度试验采用《活性粉末混凝土(GB/T 31387—2015)》[11]规定的试验方法，试验结果见表1. 表中，fp表示极限抗拉强度；εp表示极限拉应变；fcu表示立方体抗压强度；fck表示棱柱体抗压强度；Vf表示纤维体积率.

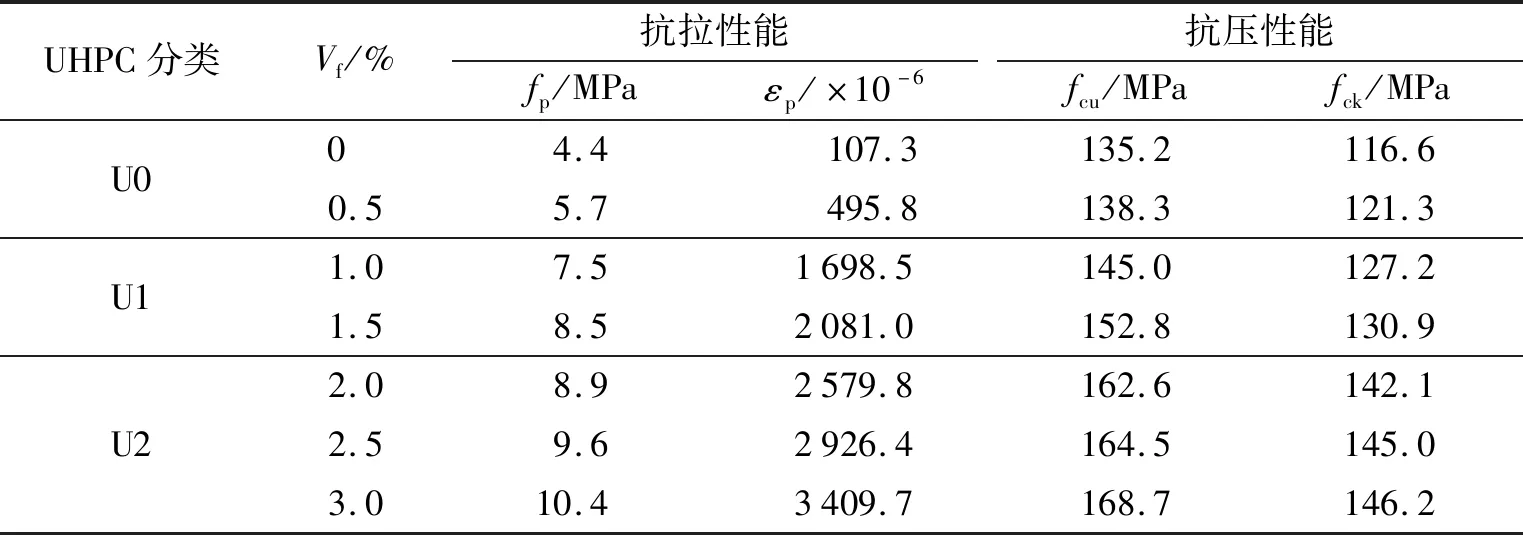
表1 材性试验结果

大量研究表明，纤维不仅影响UHPC的抗拉强度，还影响其开裂强度和极限应变[12]. 由文献[7]可知，UHPC材料根据受拉性能可分为3类. U0类：不掺纤维或纤维掺量很少，受拉开裂后，截面开裂混凝土退出工作，裂缝不断扩大，受拉试件破坏，抗拉强度等于或略大于开裂强度，受拉性能与普通混凝土相似； U1类：掺有一定量的钢纤维，受拉开裂后，由于钢纤维的桥连作用，开裂截面并未退出工作，钢纤维被逐渐拔出，其抗拉强度大于开裂强度，受拉应力-应变曲线有明显的应变硬化现象，与钢筋受拉性能相似，极限拉应变小于钢筋的屈服拉应变(取一般钢筋的屈服拉应变εy为2 100×10-6)； U2类：掺较多量的钢纤维，受拉应力-应变曲线与U1类材料相似，抗拉强度亦大于开裂强度，也具有明显的应变硬化现象，但其极限拉应变大于钢筋的屈服应变.

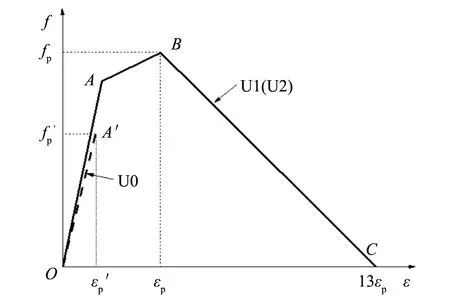
图1 UHPC抗拉应力-应变关系简化曲线Fig.1 Simplified curve of UHPC tensile stress-strain relationship

UHPC的受拉应力-应变曲线可简化成图1的形式，U1或U2类可简化成图1中的粗实线，经历了弹性段(OA段)、 应变硬化段(AB段)和软化段(BC段)，其在B点达到受拉极限； U0类可简化成图1中的粗虚线，只经历了弹性段(OA′段)，其在A′点达到受拉极限，图中f′p和ε′p分别表示弹性段A′点处的应力和应变； 图1中A(A′)点即为开裂点.

1.2 不同截面形式的R-UHPC梁

为考察截面形式对UHPC抗拉强度在R-UHPC梁抗弯承载力中贡献率的影响，取截面分别为矩形、 箱形、 T形的文献[7]、 [13]和[8]的试验梁为分析的原始对象，各梁的截面尺寸如图2所示.

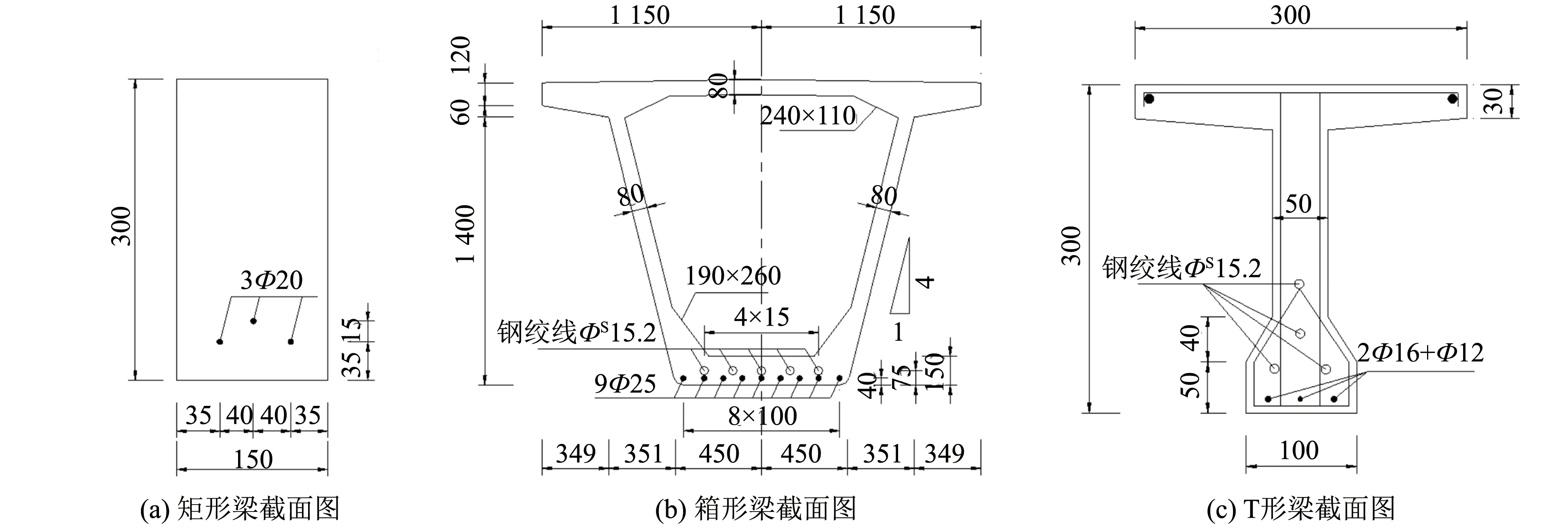
图2 不同截面形式图(单位：mm)Fig.2 Figure of different cross-section type(unit：mm)

在上述的试验梁中，箱梁为足尺试件，其他两个为模型试件，截面尺寸相差较大，跨径、 配筋率、 加载方式也不同，不利于比较. 为此，以图2中文献[7]的B2矩形试验梁为基准，对箱梁和T梁重新设计成与B2梁截面积(45 000 mm2)、 纵筋配筋率(2.4%)、 跨径(3 300 mm)、 加载方式(对称两点加载)相同或相近的梁，截面尺寸见图3. 图2(a)和图3(a)、 (b)这样截面积和配筋率相同的3种梁，具有相同的UHPC材料用量和配筋量，就是本研究的对象.

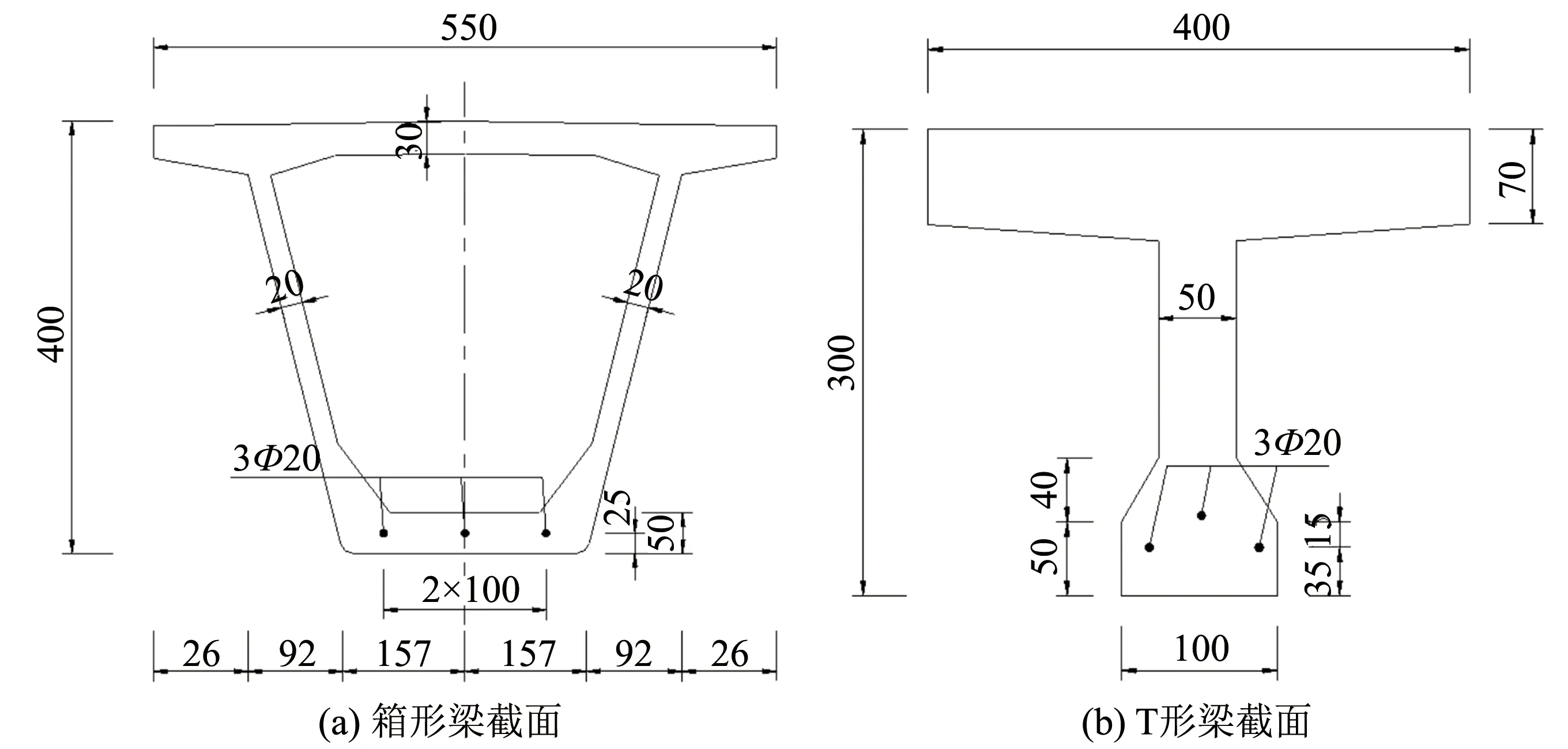
图3 等效梁截面示意图(单位：mm)Fig.3 Figure of equivalent beam cross-section(unit：mm)

2 计算分析

2.1 R-UHPC梁抗弯承载力计算方法

由节1.1可知，采用U0、 U1和U2三类UHPC材料的R-UHPC梁，在破坏时截面的应变分布各不相同. U0类材料与普通混凝土材料相似，不考虑抗拉强度对截面抗弯承载力的贡献，可按普通混凝土梁的计算方法.

对U1与U2类，受拉钢筋屈服、 截面破坏时，U1类材料的受拉区边缘进入到应力-应变曲线软化段，而U2类材料的受拉区边缘达到其抗拉强度. 抗弯承载力计算仍服从平截面假定，由图1简化的UHPC应力-应变关系曲线，不难得到U1与U2类的R-UHPC梁达到极限承载力时的正截面抗弯应变、 应力分布图和相应的抗弯承载力计算公式，详见文献[7].

文献[7]已验证了上述方法对矩形梁的适用性. 分别对文献[13]和[8]的箱梁、 T形梁按上述的方法进行计算，文献[13]足尺试验箱梁，最大承载能力加载值为1.815 MN，用本文方法计算值为1.821 MN，误差0.33%，计算方法适用于箱梁； 文献[8]中B2试验梁为T形梁，承载力矩为249.5 kN·m，计算值为241.5 kN·m，误差为3.2%，计算方法也适用于T形梁.

2.2 承载力计算

对节1.2的21根R-UHPC梁进行抗弯承载力计算. 计算时，钢筋屈服强度fy为462 MPa，极限强度fs为570 MPa； UHPC的材性取节1.1表1的实测值. 按文献[7]的计算方法，考虑UHPC抗拉贡献时的抗弯承载力计算值记为Mu，不考虑抗拉强度贡献时抗弯承载力计算值记为M′u，分别计算不同纤维体积率是否考虑UHPC抗拉性能时矩形、 箱形和T形3类截面梁的抗弯承载力，见表2.

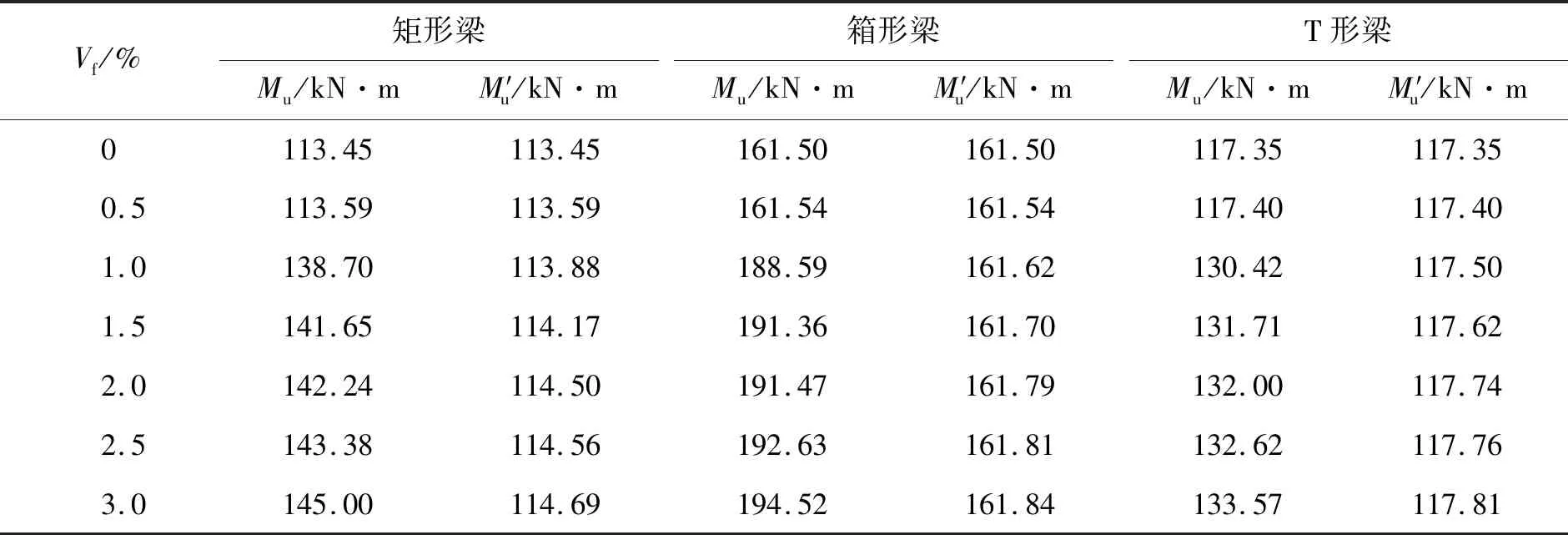
表2 是否考虑UHPC抗拉性能计算的不同R-UHPC梁抗弯承载力

由表2可知，UHPC材料用量和配筋量相同的情况下，等截面高度的矩形梁和T形梁，在考虑UHPC抗拉强度对抗弯承载力贡献时，矩形梁由于受拉区截面积较大，其抗弯承载力大于T形梁； 不考虑UHPC抗拉强度的贡献时，T形梁由于受压区截面积较大，其抗弯承载力大于矩形梁； 等截面积的箱形梁由于截面高度较矩形和T形梁高，宽度也较宽，其梁截面抗弯承载力最大.

由表3可知，UHPC抗拉强度的贡献率、 受拉区面积比均为：矩形梁>箱形梁>T形梁. 因此，截面形式对R-UHPC梁中UHPC抗拉强度贡献率的影响，不容忽视.

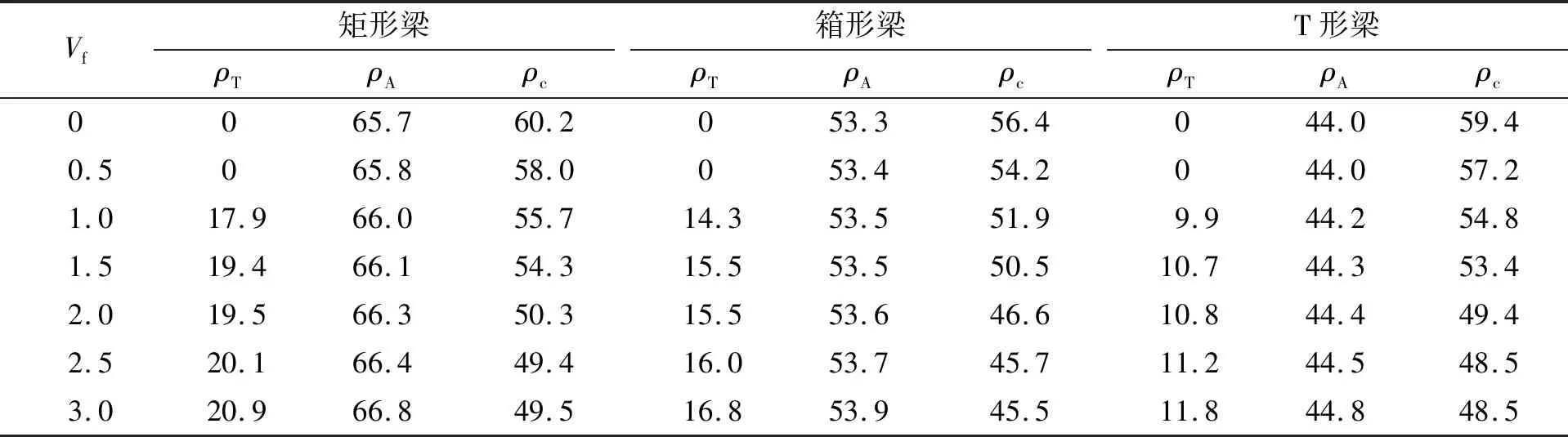
表3 UHPC抗拉性能对R-UHPC梁抗弯承载力影响

3 计算结果分析

将表3中UHPC抗拉强度和抗压强度对R-UHPC梁的抗弯承载力贡献率与UHPC的纤维掺量关系曲线，分别绘于图4、 5.

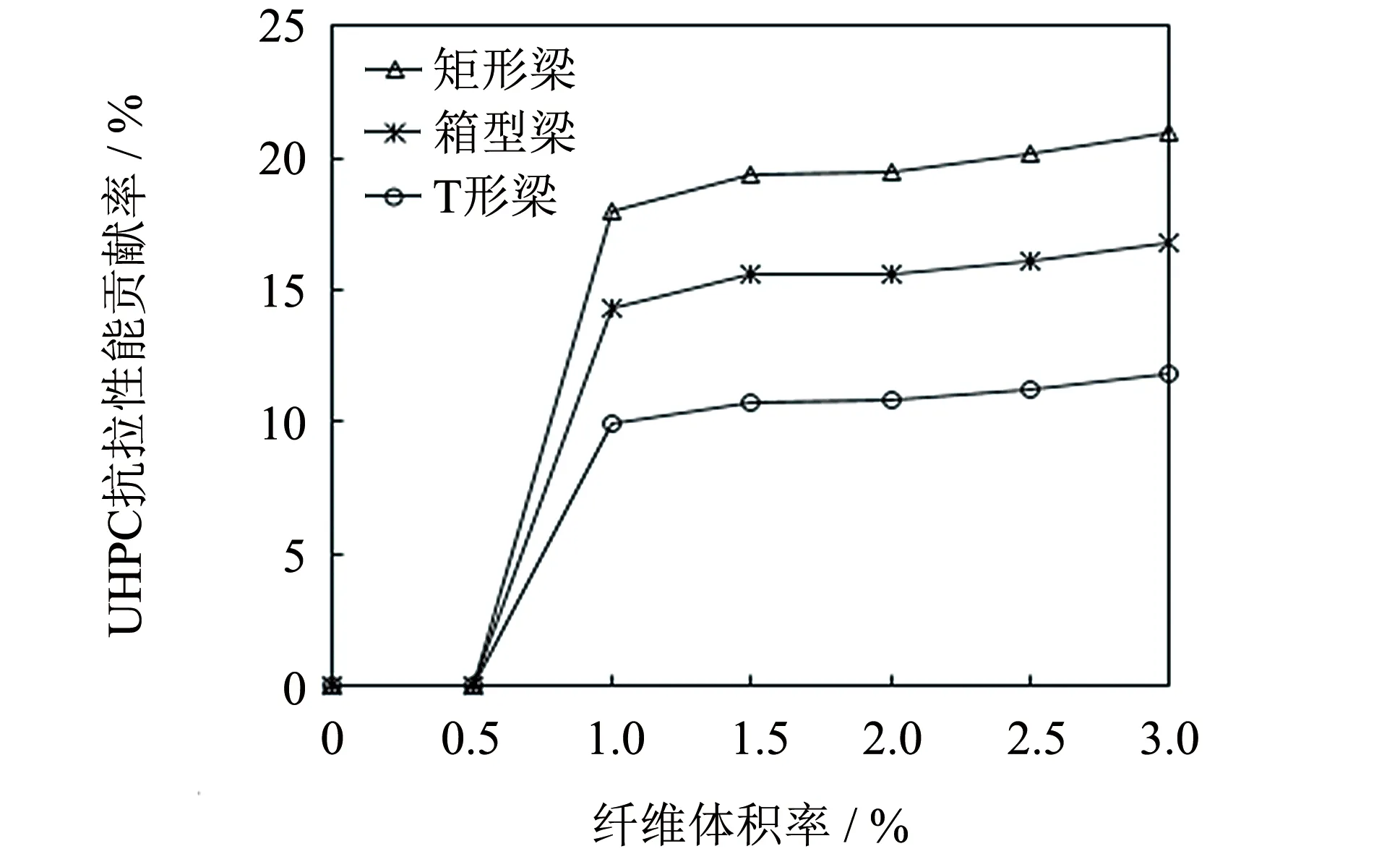
图4 抗拉强度贡献率Fig.4 Tensile strength contribution rate

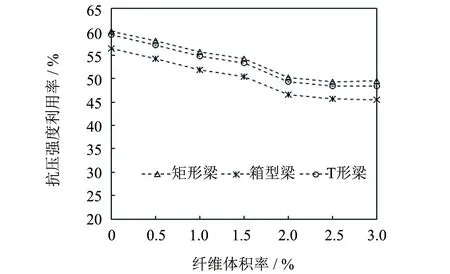
图5 抗压强度利用率Fig.5 Compressive strength utilization rate

3.1 抗拉强度贡献率

从图4可知，3种截面的关系曲线的发展规律相似. 当钢纤维掺量为0和0.5%时，为U0类，按普通混凝土抗弯承载力的计算方法，计算时未考虑其抗拉强度的贡献，故图4中计算的抗拉强度贡献率为零. 当钢纤维掺量从0.5%增加到1.0%时，UHPC材料的抗拉强度大幅上升，因此其贡献率也高速增加. 当钢纤维掺量为1.0%和1.5%时，为U1类，这一阶段UHPC极限拉应变小于钢筋屈服应变，钢筋屈服时，梁底UHPC的拉应力部分已过峰值，进入软化段，抗拉强度增长放缓，因此其贡献率增幅变缓. 此后，当纤维掺量增大到2.0%及以上时，为U2类，UHPC的极限拉应变大于钢筋屈服应变，钢筋屈服时，受拉区UHPC拉应力达到其抗拉强度，随着钢纤维掺量的增加，抗拉强度贡献率还有增长，但增幅很缓.

UHPC的抗拉强度主要来自于钢纤维掺量的贡献，随着钢纤维掺量的增多，其抗拉强度随之提高，具体到本研究的UHPC材料，由表1可知，钢纤维应该有一定的掺量，掺量应不小于1.0%，否则不能发挥其抗拉强度的作用. 纤维掺量最好大于2.0%，即采用U2类UHPC材料. 瑞士和法国规范[3-4]都规定UHPC中钢纤维掺量要大于2.0%，称之为UHPFRC(超高性能纤维增强混凝土).

从图4还可以看出，UHPC抗拉强度的贡献率，也与截面形式有关. 总体而言，贡献率：矩形梁>箱形梁>T形梁. 所有曲线在钢纤维掺量为1.0%时有明显拐点，此时，UHPC抗拉强度的贡献率，矩形梁为17.9%，箱形梁为14.3%，T形梁为9.9%，抗拉强度的贡献率较钢纤维掺量为0.5%增大明显. 当纤维掺量不小于2.0%时，也即U2类UHPC时，3种截面的贡献率，矩形梁大于19.5%，箱形梁大于15.5%，T形梁大于10.8%.

因此，对纤维掺量1.0%以上U1和U2类UHPC的矩形梁和箱形梁，其抗拉强度贡献率均超过10%，宜考虑其抗拉强度对R-UHPC梁抗弯承载力的贡献，最好是U2类. 采用U1、 U2类UHPC材料计算梁截面抗弯承载力时，UHPC抗拉强度的贡献，矩形梁应考虑，箱形梁可考虑，T形梁可不考虑.

相同材料用量和配筋量情况下，矩形梁需要增加桥面系才能获得与T形梁或箱形梁相同的使用功能，普通混凝土梁实际工程中多采用T形梁或箱形梁. 在UHPC梁截面设计时，与普通混凝土梁不同，若考虑抗拉强度的贡献，宜采用箱形梁，当然也宜采用下缘面积较大的I形或工形梁.

3.2 抗压强度利用率

UHPC具有极高的抗压强度，早期其抗压强度的最低值均定得较高，如法国(AFGC)指南[4]、 日本(JSCE)指南[14]均定为150 MPa，韩国(KSCE)指南[15]则高达180 MPa； 近年来有降低趋势，如法国标准NF P 18-470[15]定为130 MPa，瑞士SIA 2052[3]定为120 MPa. 我国的《活性粉末混凝土(GB/T 31387—2015)》[11]规定的仅为100 MPa. 文献[16]建议UHPC抗压强度最低要求定在120～130 MPa之间较为合适. 节1.1试验的7组UHPC的抗压强度也都在130 MPa以上，从实践来看，制备出抗压强度在130 MPa以上的UHPC已无技术门槛. 以按各自UHPC的实际强度在R-UHPC梁中的利用率，将21根梁的计算结果绘于图5.

由图5可知，抗压强度利用率在45.5%～60.2%，最大仅60.2%，均属于少筋梁，抗压强度利用率偏低. 由节1.1可知，抗压强度随纤维掺量增大而提高，所以抗压强度利用率随纤维掺量的增大而下降. 从抗压强度利用率来说，UHPC最低抗压强度标准的降低，是合理的.

因此，受压区采用较低强度的普通混凝土，组成UHPC-NC(UHPC-普通混凝土)叠合梁，也是目前研究热点之一[17-18]. 同时，为了改善R-UHPC梁呈少筋梁的现象，可采用提高截面拉区受力的措施，如加大受拉区钢筋用量、 使用高强度的预应力钢绞线等，实际工程应用中多采用的是预应力UHPC梁[19-20].

由图5还可知，抗压强度利用率从高到低的顺序为：矩形梁>T形梁>箱形梁. 序列与抗拉强度略有不同，这是由于箱形梁梁高较高，截面惯性矩较大，导致截面抵抗矩较大，从而梁顶压应力较低，抗压强度利用率最小. 矩形梁和T形梁等高，但T形梁截面抵抗矩大于矩形，所以矩形梁抗压强度利用率大于T形梁.

4 结语

1) 进行了7组不同钢纤维掺量的UHPC材性试验，无纤维和仅掺0.5%的纤维，受拉破坏呈单裂缝脆性破坏，无硬化段或硬化段极短，可归为U0类UHPC； 掺量为1.0%时，有相当长的硬化段，但极限应变小于钢筋屈服应变，可归为U1类UHPC； 掺量为2.0%、 2.5%和3.0%的，有硬化段，且极限应变大于钢筋屈服应变，可归为U2类UHPC.

2) UHPC抗拉强度的贡献率，与截面形式有关. 3种截面的贡献率：矩形梁>箱形梁>T形梁. 对纤维掺量1.0%以上U1和U2类UHPC的矩形梁或箱形梁，其抗拉强度贡献率均超过10%，宜考虑其抗拉强度对R-UHPC梁抗弯承载力的贡献.

3) 材料设计时，若考虑UHPC抗拉强度的作用，UHPC材料应具有相应的抗拉性能，宜采用U2类材料. 对于本文的UHPC，掺量应不小于2.0%.

4) 截面设计时，UHPC抗拉强度的贡献，矩形梁应考虑，箱形梁可考虑，T形梁可不考虑. 截面设计时，宜采用箱形、 I形或工形梁.

5) 工程应用时，抗压强度利用率随纤维掺量的增大而下降，利用率在45.5%～60.2%范围，抗压强度利用率偏低. 因此，建议实际工程中可应用UHPC-NC叠合梁或预应力UHPC梁.