改进bang-bang控制的微网VSG自适应虚拟惯量控制策略
钱 凯,高飞翎,周勋甜,邵雪峰,李 劲,温步瀛
(1. 宁波市电力设计院有限公司,浙江 宁波 315000; 2. 福州大学电气工程与自动化学院,福建 福州 350108)
0 引言
随着传统石化能源的枯竭,能源结构的变革已经成为我国能源改革的重点. 逆变器是大部分新能源与电网之间的电能交换接口,基于逆变器连接的新能源无法像传统的同步发电机一样为系统提供惯性支撑,导致系统发生扰动时各电能参数响应过快. 因此,新能源还需具备相应的频率支撑能力,以维持电网的安全稳定运行[1-4].
为使新能源具备调频的功能,有学者提出下垂控制方法[5-6],模拟同步发电机实现一次调频功能. 但是,采用下垂控制的新能源仍然没有为电网提供惯性支撑的能力,因此当系统中有功负载突变时,电网频率会由于惯性的缺失而出现频率快速抖动的现象.
为使新能源具备惯性支撑的能力,文献[7-10]提出了虚拟同步机(virtual synchronous generator, VSG)的概念,从外特性上模拟同步发电机,在实现一次调频与调压功能的基础上,还实现了惯性支撑功能. 文献[11]对比了风电机组中各种惯量控制方法的效果,证明VSG策略能提高系统在弱电网工况下的稳定性. 文献[12]结合同步发电机的功角曲线,使虚拟惯量的大小根据VSG频率的变化率自适应线性变化. 文献[13]提出一种基于bang-bang控制的VSG控制算法,虚拟惯量随着频率的变化而改变为设定的最大值或最小值,提高系统频率的稳定性,但是没有给出虚拟惯量最值的整定方法. 文献[14-15]都以储能容量为约束整定参数自适应控制策略中虚拟惯量的取值范围,从而为VSG在工程中的应用提供一定参考.
本研究提出一种基于改进bang-bang控制的VSG自适应虚拟惯量控制策略. 为减少稳态时虚拟惯量抖动,设定一个频率稳态区间,并对于该稳态区间设定一个相应的稳态惯量. 当频率超出稳态区间时,虚拟惯量随频率的变化率以及偏差量自适应地改变为设定的最大值或最小值. 最后,利用仿真验证了所提方法的有效性.
1 VSG基本原理
VSG的基本原理框图如图1所示. 图中:L1为逆变器侧电感,C为滤波电容,L2为网侧电感,Rg和Lg为线路等效阻抗. 通过VSG控制环节后得到的虚拟电动势Er与虚拟功角θ,经过虚拟阻抗[16]控制环节,使有功环与无功环解耦,得到参考电流Iref,最后经脉宽调制(PWM)控制三相逆变桥中各开关的开断,实现整个VSG系统的控制. 加入虚拟阻抗后Iref和Er以及θ之间的关系式如下:
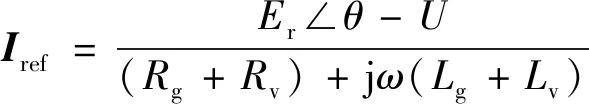
(1)
式中:Rv为虚拟电阻;Lv为虚拟电感;U为公共耦合点电压.
VSG中有功环控制环节模拟极对数为1的同步发电机的转子运动方程为:

(2)
式中:J为转动惯量;ω为转子角速度;Pm与Pe分别为机械功率与电磁功率;ωN为转子额定角速度;Dp为阻尼系数;θ为功角.
为实现微网模式下频率的无差调节,在阻尼环节并联一个积分器,实现有功环二次调频的功能[17]. 控制框图如图2所示. 其中,ki为积分增益;Qe为输出的无功功率;Qref为无功功率的给定值.
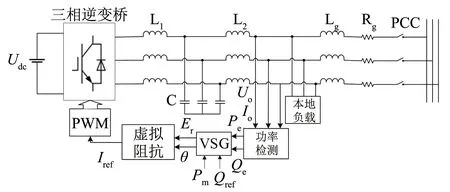
图1 VSG的基本原理框图Fig.1 Principle block diagram of VSG
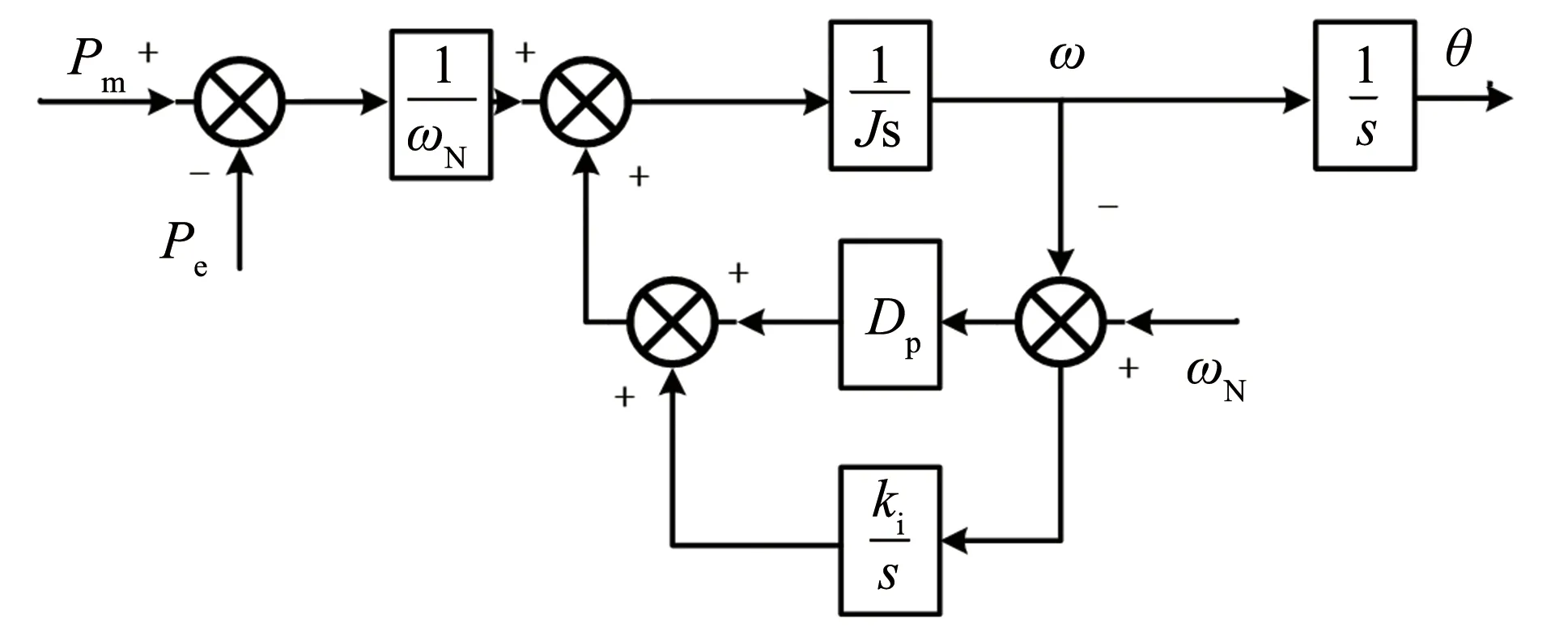
图2 具有二次调频功能的VSG有功环Fig.2 Active-power loop of the VSG with the function of secondary frequency regulation
2 自适应虚拟惯量控制策略
式(2)可化为以下形式:
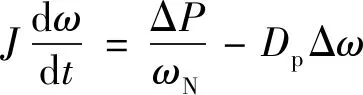
(3)
其中:ΔP为有功功率偏差; Δω为转子角速度偏差量.
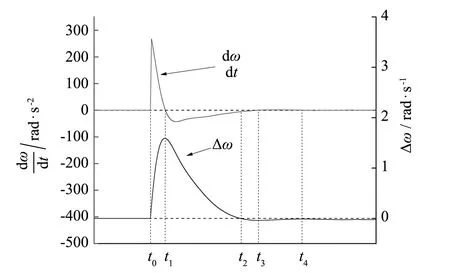
图3 负载突然减小时dω/dt和Δω的变化曲线图Fig.3 Relationship between dω/dt and Δω of load shedding
当负载突然减小时,转子角速度变化率dω/dt与转子角速度偏差Δω的变化如图3所示. 结合式(3),分析虚拟惯量变化情况与转子角速度的关系.
分析t0~t1区间,t0时刻负载突然减小,即ΔP突然增大,根据式(3)与图3可知,Δω在t0时刻不变,这导致J(dω/dt)急剧增大,因为J为固定值,所以dω/dt突增. 因为Δω在t0时刻后开始上升,所以dω/dt在突增至最大值后开始下降,直至t1时刻降为0,而此时Δω上升至最大值. 结合式(3)可知,若在t0~t1区间,适当增大虚拟惯量J可减小dω/dt突变量,进而减小转子角速度偏差量Δω.
分析t1~t2区间,Δω开始回落,直至t2时刻降为0,此时dω/dt缓慢减小至最小值后回复至0,且在t1~t2区间内都小于0. 结合式(3)可知,若在t1~t2区间适当减小虚拟惯量J可减小dω/dt,即增大|dω/dt|使得Δω更快地回复至0.
t2~t3区间和t3~t4区间的情况与t0~t1区间和t1~t2区间的情况类似,都需要适当改变虚拟惯量的大小以获得更好的频率响应特性.
对于传统的基于bang-bang控制的自适应虚拟惯量策略[13],其虚拟惯量随频率的变化率及偏差量乘积的正负自适应地变为给定的最大值或最小值. 在此基础上,提出基于改进bang-bang控制的自适应虚拟惯量策略. 设定一个频率稳态区间,减少频率因检测精度等原因使得稳态时虚拟惯量抖动,间接造成频率抖动的问题. 当频率超出稳态区间时,虚拟惯量随频率的变化率以及偏差量乘积的正负自适应地改变为设定的最大值或最小值. 同时为频率稳态区间设定一个稳态惯量,该值介于虚拟惯量的最大值与最小值之间. 当频率在稳态区间时,虚拟惯量自适应地改变为稳态惯量,避免因惯量过大而导致频率响应过慢或因惯量过小导致频率受到扰动时造成频率的偏差量过大. 具体策略如下式所示:
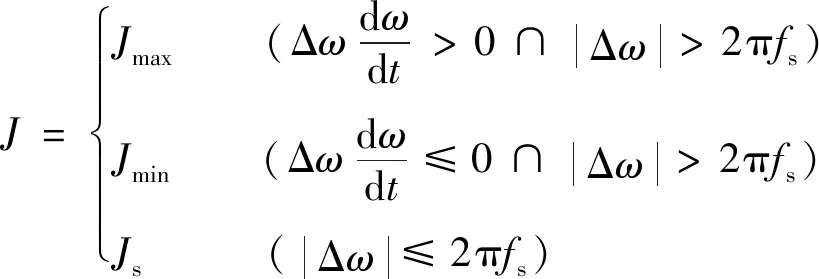
(4)
式中:Jmax、Jmin、Js分别为虚拟惯量的可取的最大值、 最小值以及稳态时的固定值;fs为稳态区间的频率偏差量. 虚拟惯量的取值范围、 稳态惯量的选取在后续章节中由小信号分析模型获得.
3 小信号模型
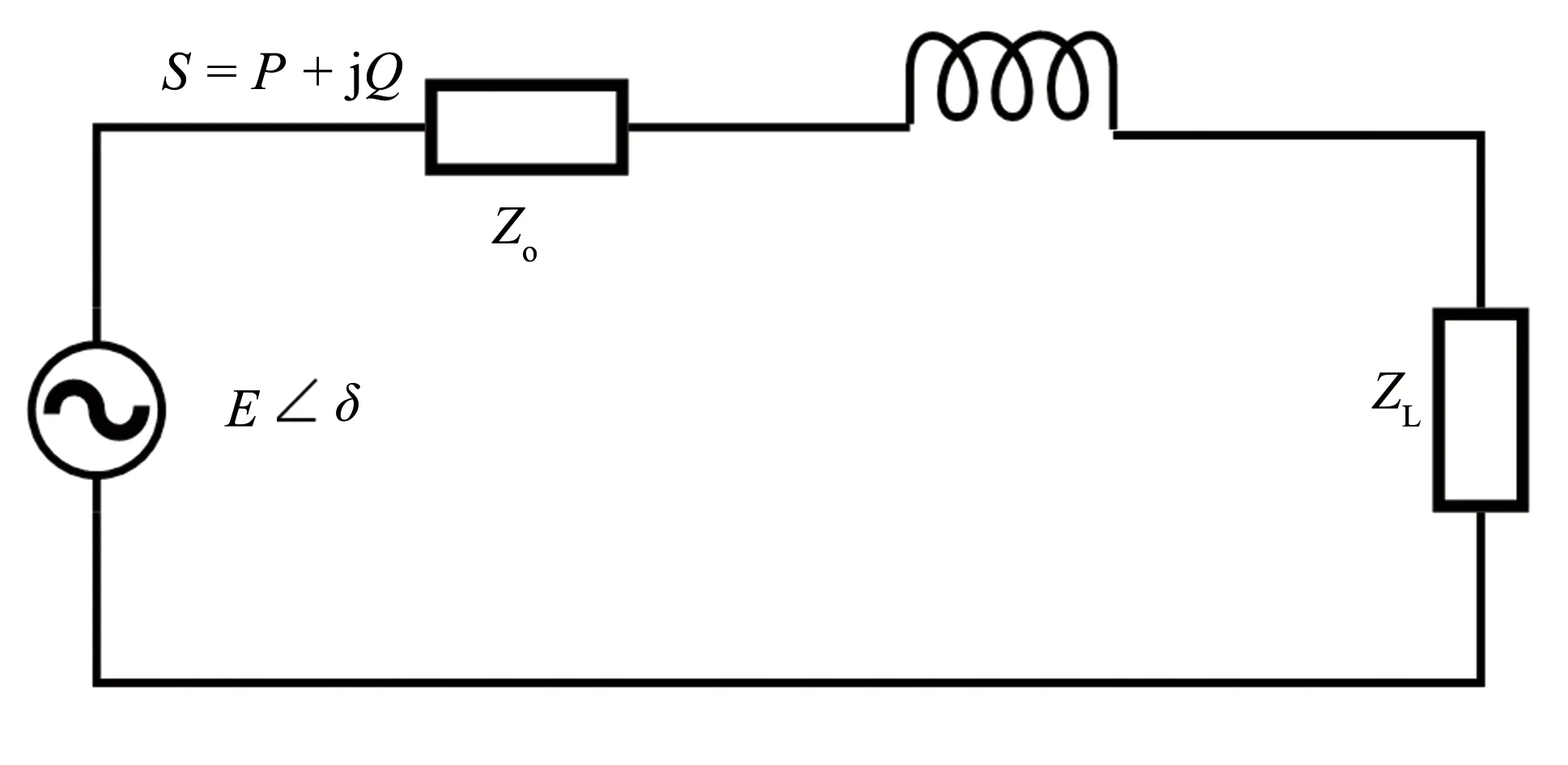
图4 微网模式下逆变器等效电路Fig.4 Equivalent circuit of inverter under island mode
微网模式下VSG的等效电路如图4所示. 其中,逆变器输出电压为E∠δ;Zo为逆变器输出阻抗;ZL为负载阻抗; 逆变器输出的功率为S=P+jQ,设输出阻抗与负载阻抗之和为R+jX[17-18],则:

(5)
设静态工作点为(ES,δS),对式(5)两端进行求导,可得功角扰动Δδ以及电压扰动ΔE与输出有功功率偏差ΔP以及无功功率偏差ΔQ之间的关系:
(6)
为简化分析,在虚拟阻抗控制下,将有功环和无功环看作近似解耦,结合图2以及式(2)、 (5)、 (6),可得微网模式下功率环的小信号等效模型,如图5所示. 根据图5求得有功环的闭环传递传递函数:
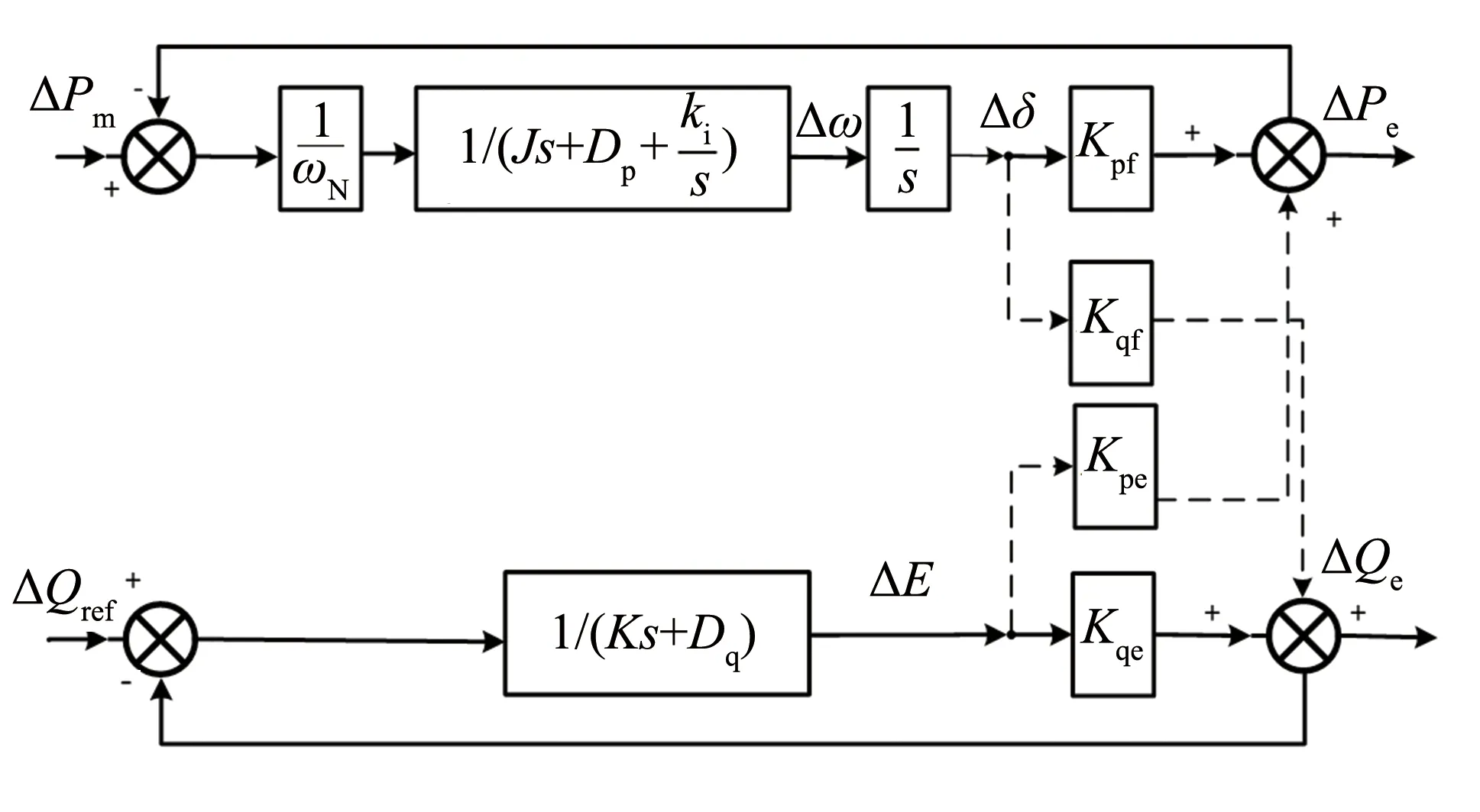
图5 VSG的小信号等效模型Fig.5 Small-signal equivalent model of VSG
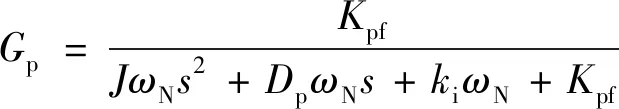
(7)
由式(7)可知,VSG有功环闭环传递函数为典型的二阶系统,其中自然振荡角频率ωNp、 阻尼比ξ和放大系数Kp为:
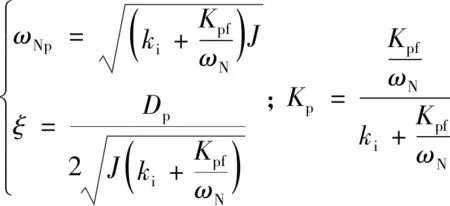
(8)
其中:Kpf的大小可由表1及式(6)计算得到,当有功环与无功环近似解耦时,Kpf约为1.0 × 105.
二阶系统稳定的条件是阻尼比ξ> 0. 为使VSG具有较快的频率响应速度,令有功环为欠阻尼环节,0 <ξ< 1. 由ξ> 0易得J> 0; 由ξ< 1可得J> 0.005 7.
根据GB/T31464-2015《电网运行准则》[19]的规定,机组一次调频需在3 s内开始响应频率故障. 假设VSG参与电网调频的响应时间ts,其约等于VSG有功环响应时间tp. 考虑一定的裕度,令tp<1 s. 典型欠阻尼二阶环节响应时间计算公式为:

(9)
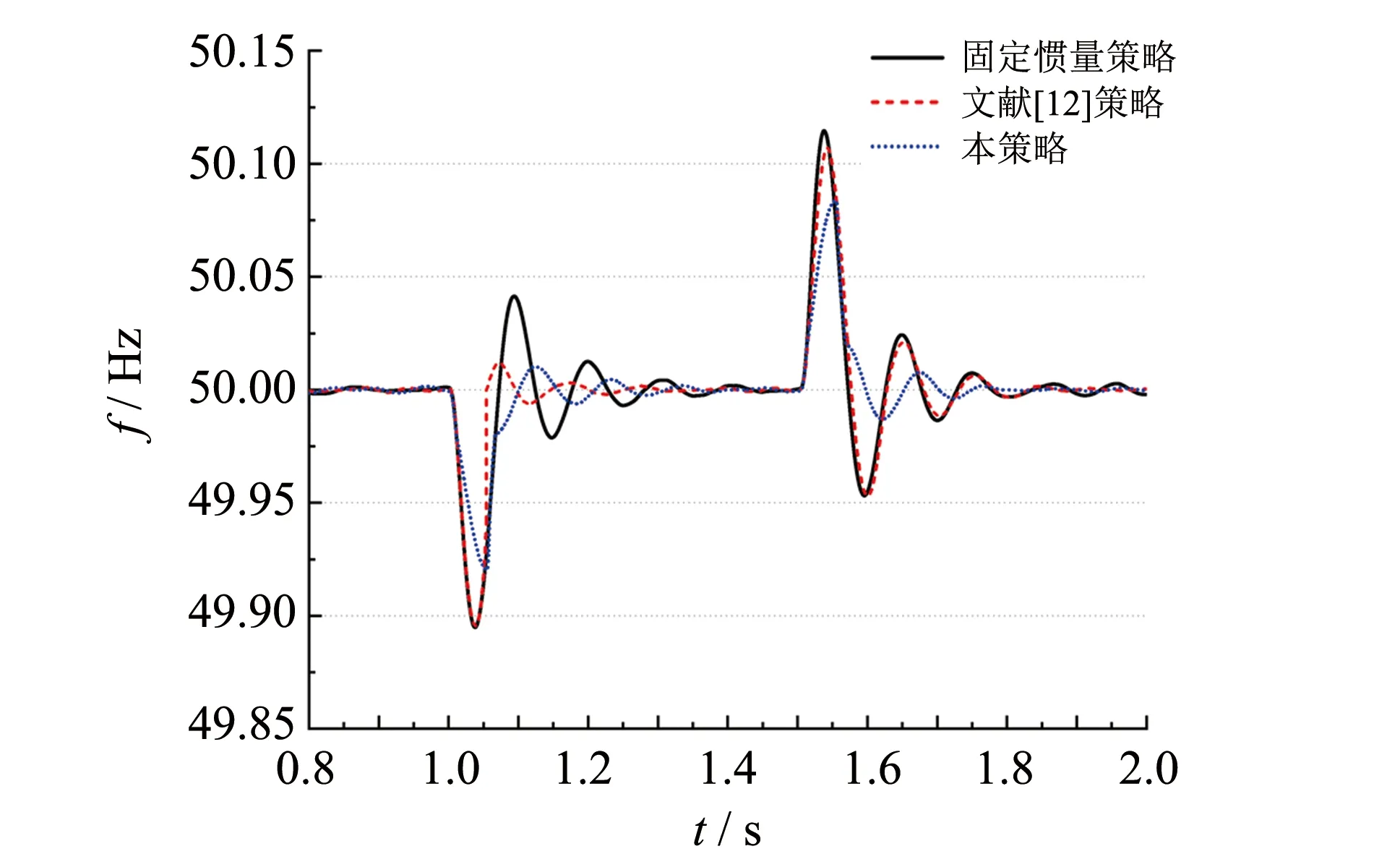
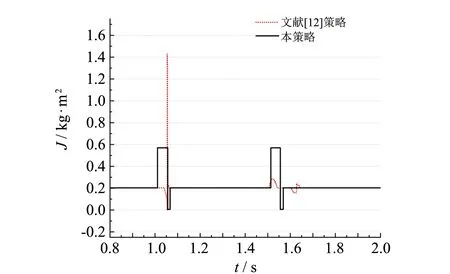
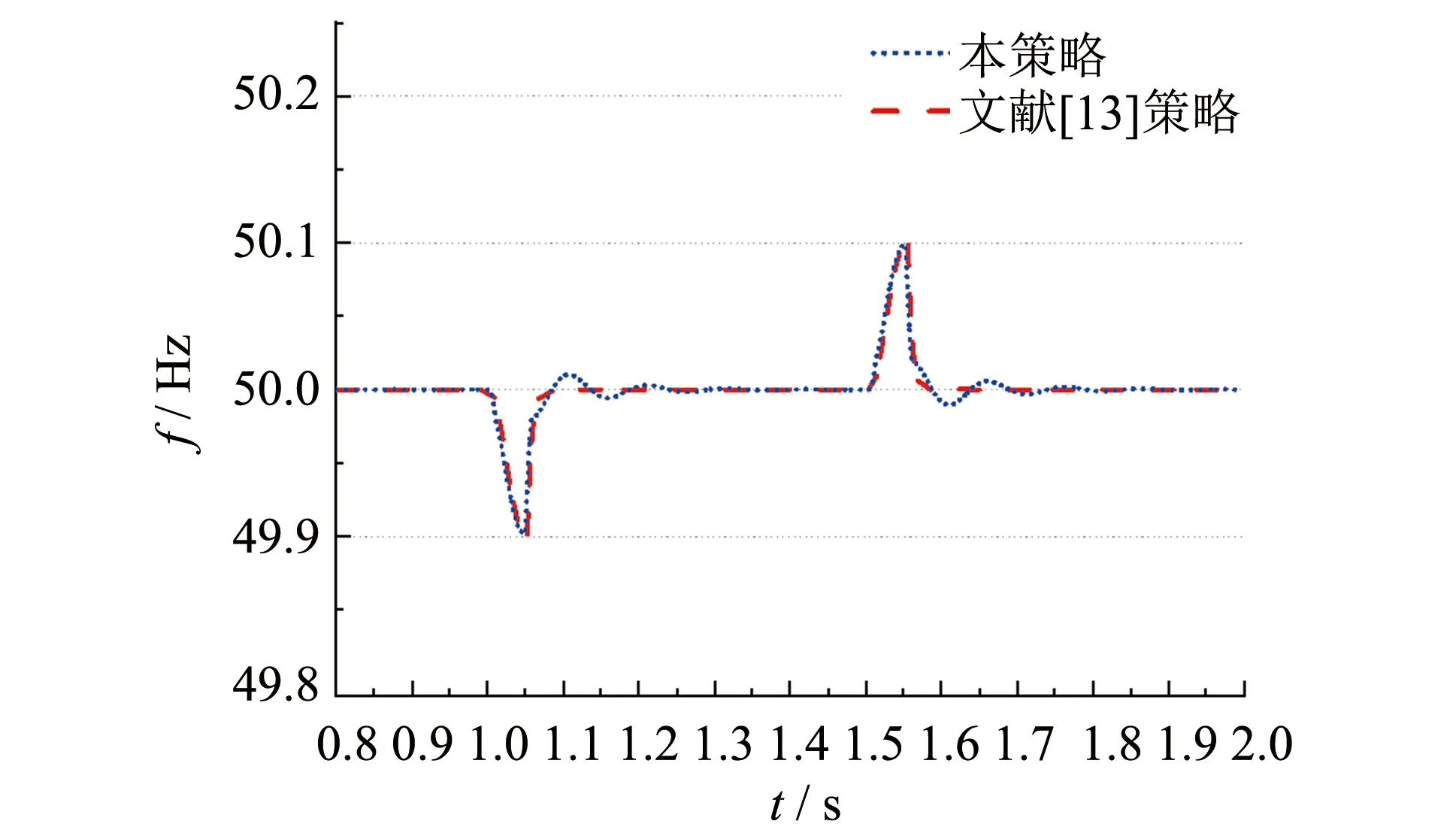
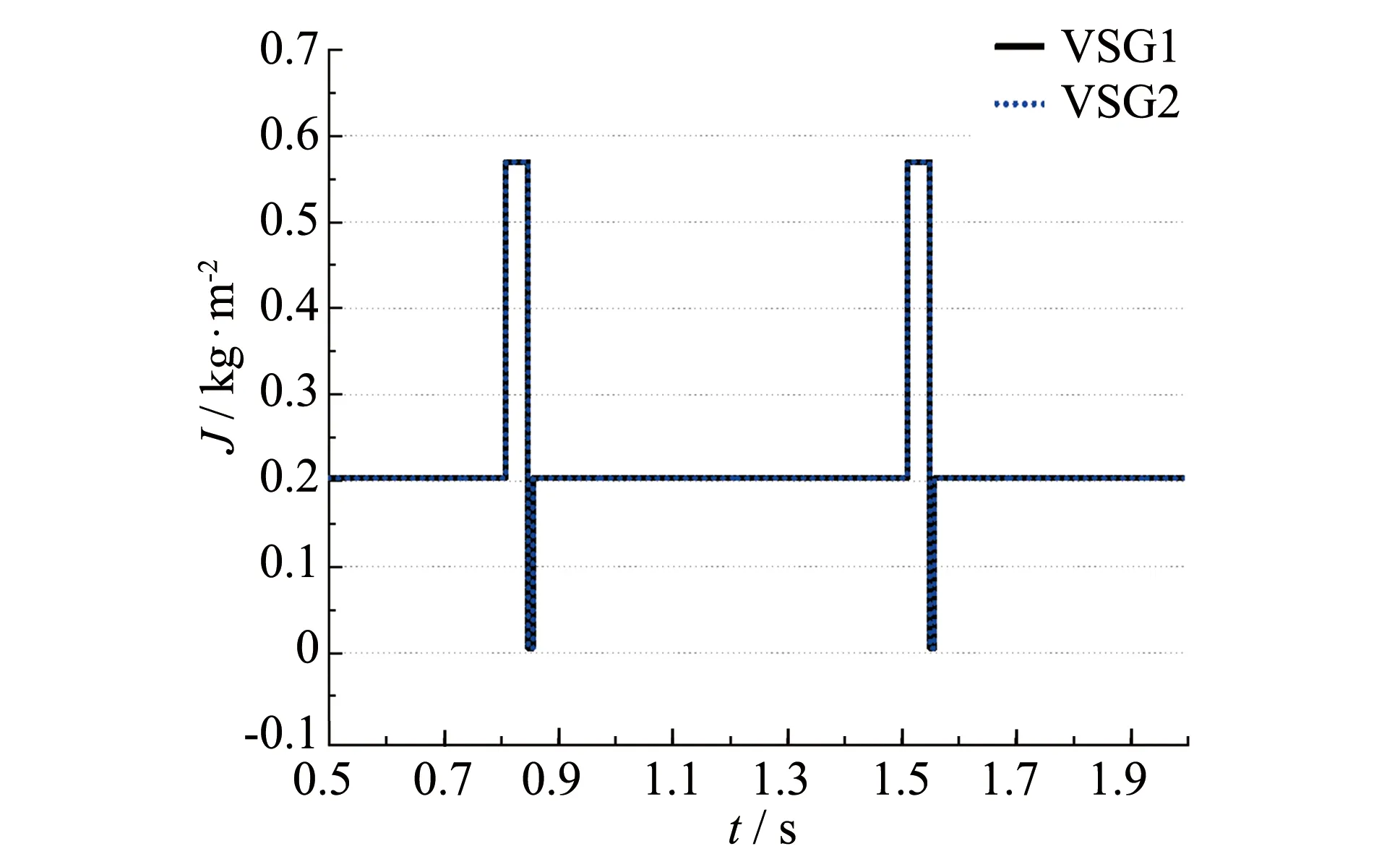
由tp< 1 s可得J< 0.57. 综上所述,J的取值范围为0.005 7 同步发电机的转子惯量J的大小与其惯性时间常数H成正比关系,其中惯性时间常数H的表达式为: (10) 其中:SN为同步发电机额定功率. 对一般的同步发电机,惯性时间常数H的数值范围在2~9 s. 考虑到VSG的响应时间不宜过慢,取惯性时间常数为2 s时对应的转子惯量为VSG系统的稳态虚拟惯量,并结合上述求得的转子惯量大小的取值范围,可求得Js=0.202 8 kg·m2. 为验证所提综合控制方案的正确性和优越性,利用Matlab/Simulink仿真软件搭建了单台VSG接阻感性负载的仿真算例. VSG系统的主要参数[17, 20]和自适应虚拟惯量参数如表1所示. 仿真系统运行在微网模式下,初始运行时接入有功负荷5 kW与无功负荷2 kvar,1 s时有功负载提升至10 kW,1.5 s时负载恢复正常,模拟系统负荷变动所带来的频率稳定性问题. 在相同的仿真条件下,对固定惯量策略、 文献[12]策略以及本策略进行对比验证,结果如图6所示. 表1 VSG综合控制方案系统部分参数设置 固定惯量策略的虚拟惯量大小设定为Js=0.202 8 kg·m2; 文献[12]策略中虚拟转子角速度变化率阈值C设为5,常数k设定为0.003,惯性时间常数的稳定值为J0=0.202 8kg·m2; 本策略参数设定如表1所示. 由图6可见,当1 s有功负载突然增加时,由于有功功率的缺失,频率开始下降. 此时,固定惯量算法与文献[12]策略的频率偏差量基本一致,为0.105 Hz,本策略为0.076 Hz(较前两者的频率偏差量降低27.6%). 当频率下降至最低值后,文献[12]策略与本策略的频率恢复稳态区间(± 0.02 Hz)的时间基本一致,而固定惯量策略在频率进入稳态区间后需经过一个振荡周期才稳定在区间内. 当1.5 s负载恢复正常时,机械功率剩余,频率上升. 固定惯量策略的频率偏差量为0.113 Hz,文献[12]策略为0.105 Hz,本策略为0.082 Hz(较固定惯量策略降低27.4%,较文献[12]策略降低21.9%). 在频率回复过程中,固定惯量策略与文献[12]策略回复速度一致,在频率进入稳态区间后,需经过一个震荡周期后才稳定在区间内; 而本策略频率回复至稳态区间后,就稳定在稳态区间内,较前两者有更短的调整时间. 虚拟惯量的变化曲线如图7所示. 由图7知,文献[12]策略的虚拟惯量只在频率变化率大的时候变动,且在1.05 s左右突增至1.42 s,超过了所求得的虚拟惯量的范围. 由于虚拟惯量大于0的限制,对文献[12]策略,其常数k的选取受到了限制,以至于出现频率变化率小而偏差量大的情况时,虚拟惯量的变化并不明显,不能有效改善系统频率响应特性,如图6与图7中1.5 s负载恢复时所展示出的情况. 而对本策略而言,当频率超出稳态区间且远离稳态区间时,虚拟惯量变大,减少频率偏差量; 靠近稳态区间时,减小虚拟惯量,加快恢复速度. 图6 三种策略的控制效果对比Fig.6 Comparison of control effects of three strategies 图7 虚拟惯量控制效果对比 Fig.7 Comparison of virtual inertia control effects 图8 本策略和文献[13]策略的控制效果对比 Fig.8 Comparison of control effects of two strategies 在相同的仿真条件下,对本策略和传统bang-bang虚拟惯量策略的控制效果进行对比(如图8所示),验证本策略可有效避免虚拟惯量在稳态时频繁产生抖动. 惯量的变化情况如图9所示. 由图8和图9可见,两者对频率的控制效果基本一致,但是在虚拟惯量的控制上相差较多. 本策略下的虚拟惯量只在频率超出稳态区间时动作. 而文献[13]所提策略,由于没有设置频率稳态区间,即使频率稳定在频率区间内,其虚拟惯量也以较高的频率在上下限之间来回阶跃. 虚拟惯量高频率的反复跳动,也使有功环阻尼在稳态运行时反复变化,增加了系统的不稳定性. 同时,对于储能电池的频繁控制也会影响其使用寿命. 图9 虚拟惯量变化情况Fig.9 Virtual inertia variation of two strategies 为验证所提控制策略的适用性,利用仿真软件搭建了两台VSG并联运行系统的仿真算例,如图10所示. 其中,VSG1与VSG2的额定容量都为10 kW. 仿真系统运行在微网模式下,初始运行时接入有功负荷10 kW,0.8 s时有功负载突升至20 kW,1.5 s时负载恢复正常,模拟系统负荷变动所带来的频率稳定性问题,观察本策略对VSG并联造成的影响,如图11~12所示. 由图中可见,本策略对并联运行的VSG同样具有较好的频率控制效果. 图10 VSG并联运行系统示意图Fig.10 Schematic diagram of VSG parallel operation system 图11 VSG1的频率控制效果对比Fig.11 Comparison of frequency control effect of VSG1 图12 VSG1与VSG2的虚拟惯量变化情况Fig.12 Virtual inertia variation of VSG1 and VSG2 提出基于改进bang-bang控制的微网VSG自适应虚拟惯量策略,在bang-bang控制的基础上设定频率稳态区间,避免由于检测精度等原因造成虚拟惯量抖动而出现频率抖动的情况. 其次,稳态惯量的设定综合考虑了频率响应时间与频率偏差量的影响. 并通过建立功率环的小信号等效模型,对虚拟惯量进行稳定性分析,确定了虚拟惯量的取值范围. 最后,通过Matlab/Simulink仿真环节对比了三种惯量算法与并联运行情况下的控制效果,验证本方法的有效性.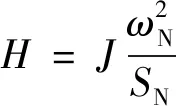
4 仿真分析




5 结语

