利用粒子群优化的极限学习机入侵检测算法
耿永利,李永忠,陈兴亮
(1. 镇江高等职业技术学校计算机教研室,江苏 镇江 212016; 2. 江苏科技大学计算机学院,江苏 镇江 212003)
0 引言
计算机网络安全一直是一个亟待解决的棘手问题,如何识别网络攻击是一个关键问题. 网络入侵[1]指未经过用户授权而对系统资源进行非法的操作行为,如何预防入侵行为成为网络安全领域的研究热点. 粒子群优化算法[2](particle swarm optimization, PSO)是一种基于群体智能的,通过粒子的最优积累和跟随粒子群的最优来实现寻优目的的方法,在人工智能和入侵检测领域的应用都较为广泛. 文献[3]提出了极限学习机(extreme learning machine,ELM)的概念,其比传统的误差反向传播算法[4]具有更快的训练速度以及更强的泛化能力. 之后,文献[5]在极限学习机的实践基础上又对核极限学习机(kernel extreme learning machine, KELM)进行了研究. 核极限学习机将核学习和标准化的优化方法结合起来求出最优解,同时减少了确定最优隐节点的过程,比ELM具有更好的泛化能力[6-7],减少了大量的先验工作. 本研究提出一种利用粒子群优化的极限学习机入侵检测算法,并通过检测模型进行检测,达到检测的预期效果. 首先针对网络数据数量庞大,特征分布离散等问题,该模型采用改进的粒子群优化k均值算法处理数据,增加入侵数据集中相似数据的聚集度; 然后将数据进行10-CV分割,利用粒子群算法全局搜索能力的优点优化多核极限学习机的参数,最后将10-CV的数据通过优化的多核极限学习机进行训练检测. 本文的入侵检测模型是利用改进的粒子群优化算法对核极限学习机的核参数进行优化,并以入侵检测率作为适应函数,不断对核参数进行优化,直到满足条件为止.
1 粒子群优化算法与核极限学习机
1.1 粒子群优化算法
粒子群算法能够实现参数的最优查询[8],然而,当粒子群算法进入后期时,粒子群容易陷入局部最优状态[9-12]. 本研究采用改进的优化算法,利用粒子群的多样性度量diversity和适应度方差θ2来判断粒子群是否陷入局部最优,当粒子群的多样性或适应度方差小于设定值时,采用高斯扰动优化此时的全局最优粒子:
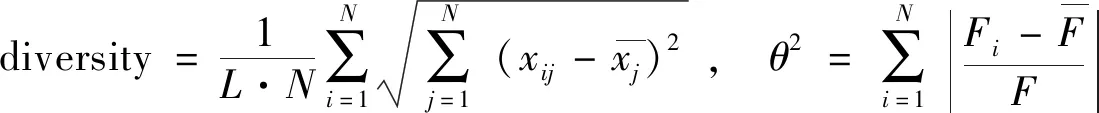
(1)
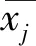
改进的粒子群算法步骤如下.
Step1初始化粒子群,包括粒子数N,最大迭代数tmax,加速因子c1,c2,惯性权重最大值和最小值wmax,wmin,以及粒子的速度范围[Vmin,Vmax],diversity∈(0,H1],θ2∈(0,H2].
Step2计算每个粒子的适应度值,粒子初始最优值设置为当前适应度值,并比较初始最优值计算出全体最优值.
Step3计算粒子的个体最优位置和全局最优位置.
Step4用下列公式更新粒子的速度和位置:

(2)

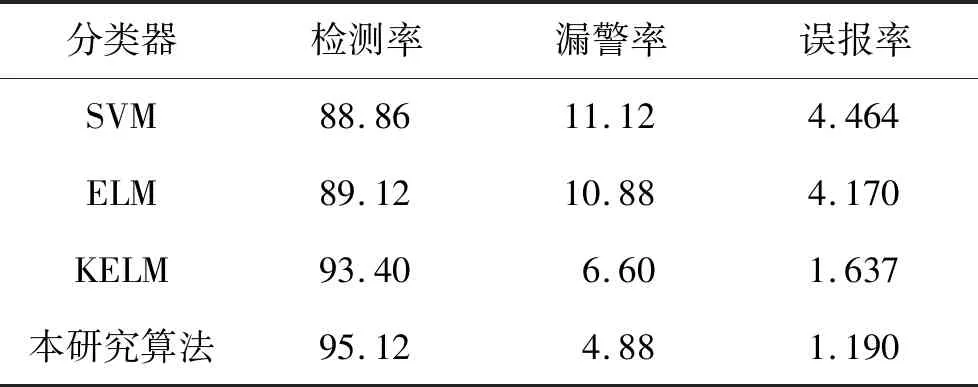
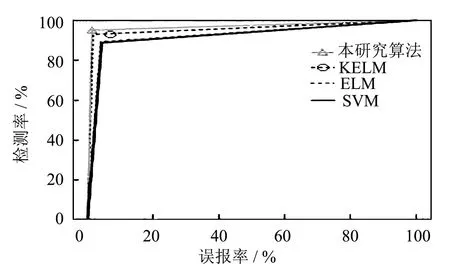
Step5利用公式(1)计算出粒子的平均距离、 适应度方差,如果di Step6利用以下公式对当前的全局最优值采用高斯扰动,并将原来的值替换成计算后的值: (3) 式中:Xmax,Xmin分别表示当前粒子中所有粒子每一维的最大值和最小值;σmax,σmin分别代表σ的上限和下限;t表示正在进行的迭代次数;tmax表示粒子最大的迭代次数. Step7对新粒子的适应度值进行计算,并对新粒子的个体最优值和全局最优值进行比较; 对新粒子的先前个体最优值和全局最优值比较,如果比较结果有更好的,就进行更新,如果没有就不更新. Step8假如迭代次数t ELM是针对单隐层前馈神经网络缺陷提出的新算法,具有较快的学习速度和较好的泛化性能[7, 13]. 假设有N个任意样本{(xi,ti),xi∈Rn,ti∈Rm},对于一个有L个隐藏神经元的ELM输出函数可表示为: (4) 多核极限学习机是将核函数代替ELM中特征矩阵运算HTH,解决了ELM算法随机初始化问题,多核极限学习机的输出函数表示为: (5) 式中:kmix(xi,xj)是多核极限学习机. 从式(5)中可看出,多核极限学习机保留了原ELM的学习速度、 泛化性能等优点,同时不需要给出原ELM的激活函数,不需要设置隐层神经元个数,只需要设定核函数的参数就能获得较高的识别率. 其中,多核极限学习机中核函数是通过线性组合多个核函数得到的新核: (6) 这里,μj是核函数的加权系数. 基于粒子群优化和核极限学习入侵检测算法(PSO-KELM)如图1所示,本研究提出的入侵检测模型的核心思想是利用改进的粒子群优化算法对核极限学习机的核参数进行优化,并以入侵检测率作为适应函数. 若测试集的检测率即粒子群的适应度值未达到指定的精度,或者迭代次数小于最大迭代次数,则继续对核参数进行优化,直到满足条件为止. 在该模型中,选取核极限学习机为入侵检测模型的分类器. 相对极限学习机而言,核极限学习机不需要激活函数和给定隐藏节点,只需要给定核函数即可,具有更快的学习效率. 由于每个核函数的自身的局限性及应用的场合有所不同,在面对数据结构不规则、 样本规模巨大及样本分布不均的应用需求时,单核函数构成的核机器会出现鲁棒性能差、 检测率低等缺陷[14]. 本研究通过核函数的分析与对比实验,得出多核极限学习机的准确度比较稳定,误报率也相对较低. 图1 粒子群优化和核极限学习入侵检测模型Fig.1 The intrusion detection model of PSO and kernel extreme learning 同时,为了结合局部函数和全局函数的优点,本实验选取的核函数为高斯核与多项式核: (7) 由公式(5)~(7)可知,在该入侵检测模型中,需要对加权系数μ、 惩罚系数γ、 指数系数s及正规化系数c进行选优. 本研究算法的多核极限学习机为: 第一步:创建应用程序并获取相应平台的商家ID标识码,也就是注册分配标识码。以支付宝为例,要想应用程序能使用支付宝移动支付,首先需要开发者到支付宝的蚂蚁金服开放平台的开发者中心中实名认证,创建登记应用,并提交审核,审核通过后会生成应用APPID,这时就可以申请开通开放产品使用权限,通过APPID应用能调用开放接口。一般来说,只需填写应用的基础信息,如应用名称、应用图标,这一部分可以在以后的开发中再更改。在开发应用中需要先选择使用场景,也就是使用类型。 (8) 算法的具体步骤如下. 在测试集中随机选取N份数据,对数据进行特征值提取和归一化处理. 设定最大适应值ε=0.95,最大迭代次数tmax=100,粒子群个数m=30,粒子群初始位置(μ,γ,s,c). Step1用核极限学习机对测试集进行学习,核极限学习机的核系数为粒子的位置(μ,γ,s,c),输出识别率即函数适应度值. Step2根据输出的适应度值确定粒子的个体最优值pbest和全体最优值gbest. Step3若gbest>0.95或者迭代次数t>100,跳转到Step6,否则,进入Step4. Step4利用改进的粒子群优化算法优化核参数. Step5重复Step1到Step3. Step6输出粒子的全局最优位置,保存全局最优位置对应的适应值. 算法中,通过核函数的Mercer性质合成多核函数,以解决单核机器中出现鲁棒性能差、 检测率低等缺陷; 然后通过高斯扰动等方式提高粒子群算法的局部搜索能力,用来优化多核极限学习机中的核参数以及正则化因子,以提高多核极限学习机的收敛速度和泛化能力. 为了验证本研究所提算法的有效性,在Matlab2012b上进行实验仿真,测试数据集选用的是目前大家公认的实用网络安全审计数据集KDD CUP 99[15]. 该数据集中有四大类攻击,分别为DOS攻击、 Probe攻击、 U2R攻击及R2L攻击, 每条记录的数据有41个特征属性. 本次实验选用了KDD CUP 99中的10%部分测试训练集作为实验数据,具体如表1所示. 表1 实验数据集 为了测试算法的性能,将测试数据集通过入侵检测模型进行检测,获得实验数据如图2所示. 由图2可知,利用改进的粒子群优化算法优化核参数时,经过17次迭代即可达到最优,此时的最优适应度即入侵检测率高达0.951 2,全局最优位置即加权系数μ=0.64,惩罚系数γ=4.12,指数系数s=2.0,正规化系数c=6.07. 同时,当迭代次数t=14时,粒子群算法陷入了局部最优,通过本研究改进的粒子群优化算法利用高斯扰动使算法跳出了局部最优. 为了进一步对所提算法的有效性进行验证,表2给出其他3种分类器与本研究提出的改进的粒子群优化核PSO-KELM分类器的性能对比结果. 图2 PSO-KELM算法的适应值曲线 Fig.2 The fitness curve of PSO-KELM algorithm 表2 分类器的性能对比 图3 分类器ROC对比曲线Fig.3 The ROC comparison curves of different classifier 由表2可知,利用改进粒子群优化核极限学习机算法的入侵检测率有明显的优势,同时,漏警率同其他分类器相比得到了降低 (表2中,检测率为检测出的入侵数据占总入侵数据百分比,漏警率为误认为正常数据的入侵数据占总入侵数据的百分比,误报率为误认为入侵数据的正常数据占总正常数据百分比). 图3中以误报率为横坐标,检测率为纵坐标分别画出SVM分类器、 ELM分类器、 KELM分类器以及本研究所提分类器的ROC对比曲线,从中可直观地看出各个分类器的性能比. 由图3可看出,改进的粒子群优化多核极限学习机的入侵检测模型明显优于其他分类器模型. 本研究提出一种基于PSO算法优化核极限学习机的入侵检测算法. 通过判断粒子的平均距离和适应度方差,决定是否采用高斯扰动对PSO进行优化, 利用优化的PSO对核极限学习机进行参数选优, 结合KDD99数据集,并通过实验证明,该算法能有效提升入侵检测算法的性能.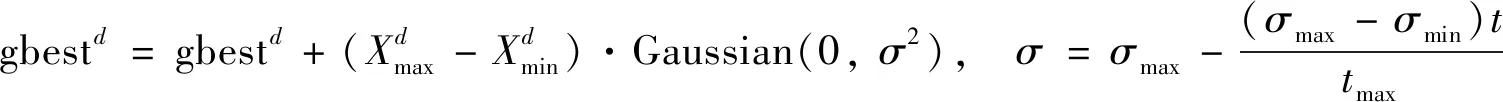
1.2 核极限学习机理论




2 基于粒子群优化和核极限学习入侵检测算法(PSO-KELM)设计与实现
2.1 入侵检测模型
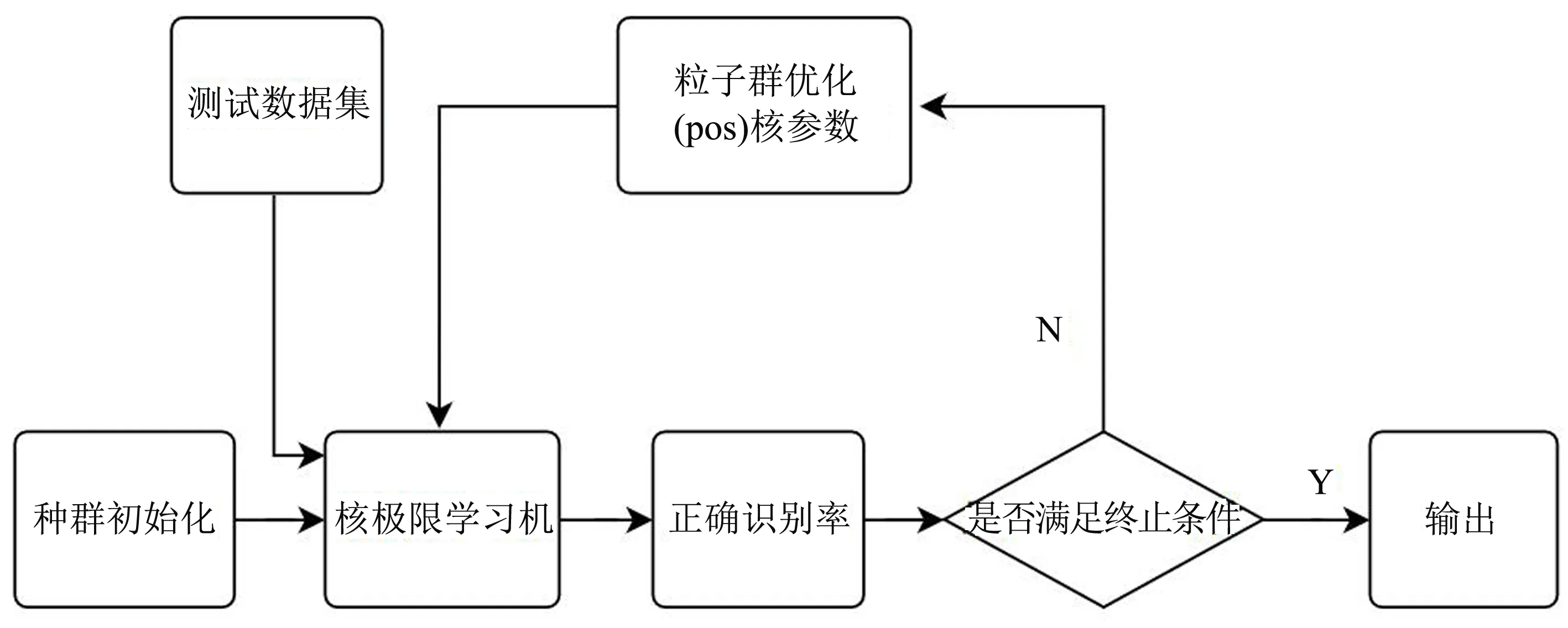
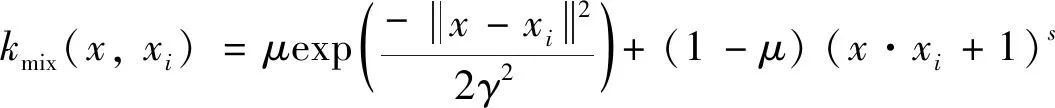
2.2 PSO-KELM算法的实现


3 仿真实验与分析
3.1 实验环境

3.2 实验结果分析

4 结语

