并联型接触器触头的电流分布特性

张槟鑫，许志红

(福建省新能源发电与电能变换重点实验室，福州大学电气工程与自动化学院，福建 福州 350108)

0 引言

工业以及居民用电负荷的增长驱动着电网规模的不断扩大，电力系统通过自身扩容和网际互联，系统负荷越来越大，正常情况下通过的电流随之增大[1-2]. 由于接触器触头材料和结构方面的瓶颈问题难以突破，单断口接触器难以满足日益增大的电网容量以及新能源领域发展的需求[3-4]，在不改变材料和机构的前提下提高接触器容量，将多台接触器并联连接运行是较为常见的方案.

风电及光伏等新能源领域的电气传动系统主电路电流等级为1.26～2.10 kA，接触器容量的提升将有利于拓宽应用场合，如大型加工设备、 光伏、 风电等新能源领域[5-6]. 据了解，控制320 t行车电机的接触器需要由8台1.00 kA接触器联锁并联构成[7]. 目前国内大容量接触器市场主要由ABB、 施耐德等公司的产品占据，且都有以并联形式扩容的相关产品. 其中ABB的AF1350～2650系列产品采用两极甚至三极动触头并联形式，施耐德LC1系列接触器则采用接线端子并联使用； 西门子公司曾将三相并联的真空断路器组成一相使用. 相比之下我国大容量接触器研究起步较晚[8]，文献[9]将2台三极1.25 kA交流接触器并联扩容成一台2.00 kA交流接触器，其扩容系数仅为1.6.

现有并联型大容量交流接触器产品均存在降容使用的现象，并联支路数为3时，其扩容系数为2.25，并联支路数为4时，其扩容系数仅为2.8左右. 可以看出, 并联方式对接触器的利用率较低，考虑到长期运行时的温升以及通断能力影响[10-11]，并联型接触器只能采取降容运行. 文献[12-13]通过数学关系表明, 具有并联结构的三相交流开关电器，触头间电磁邻近效应将会造成电流分配不均，但是仅从数学关系难以直观看出电流分布特性. 文献[14-15]将紧耦合电抗器串联在触头回路中，达到自动均流/限流的目的，然而这种电抗器设计过程复杂，成本较高，且将造成开关体积过大.

因此，要找出一种解决不均流现象的可行性方案，对大容量接触器并联运行时的触头电流分布特性研究必不可少. 本研究以课题组自行研制单极开关[16]为对象，通过对并联型接触器触头回路的磁场和电路分析，推导出各支路触头电流分布模型，并确定各支路电流大小关系； 利用Maxwell和Simplorer软件联合仿真获取各支路电流，结果与分布规律模型基本吻合. 进一步地, 研究并联型接触器在不同参数下的电流分布特性，推导扩容系数，为设计并联型大容量接触器奠定理论基础.

1 触头电流分布模型

1.1 单相并联型接触器触头电流分布模型分析

图1 单相并联型接触器触头回路等效电路 Fig.1 Equivalent circuit of single-phase parallel contactor contact circuit

单相并联型接触器触头回路等效电路如图1所示. 图中I0为干路电流，I1、I2分别为两个并联支路的触头电流，Z1和Z2为各支路接触器阻抗参数. 为简化分析，将触头电路认为是不计宽度的载流导线，当回路面积不变时，根据法拉第电磁感应定律, 有：

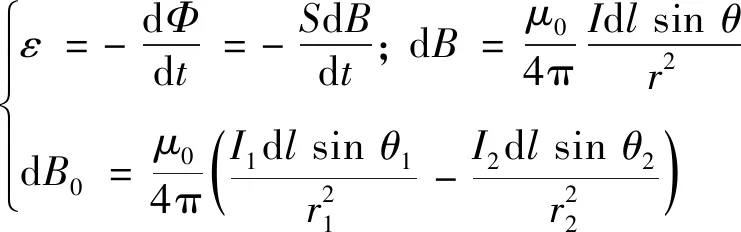
(1)

式中：ε为感应电势；S为回路面积；I为载流导线电流； dl为载流导线微元；r为电流元与空间某一点的距离；θ为两者的夹角，B0各支路电流元在闭合回路某一产生的磁感应强度之和.

假设各支路接触器阻抗参数相等，则I1=I2=I0/2. 由式(1)可知，当各支路接触器触头以并联连接运行时，结构对称，因此必定能找到在同一水平线上且r相同时的空间上两点，使得r1=r2，且满足θ1=θ2，又由于各支路电流大小相同，在单相并联回路中各支路电流元产生磁感应强度将互相抵消，整个回路包围空间不发生磁通变化，根据式(1)可以得到I1=I2=I0/2，与假设相符.

1.2 三相并联型接触器触头电流分布模型

分析A相时，假设另外两相电流均从中心线流过，且把另外两相电路看作无限长导线，其电路如图2所示.

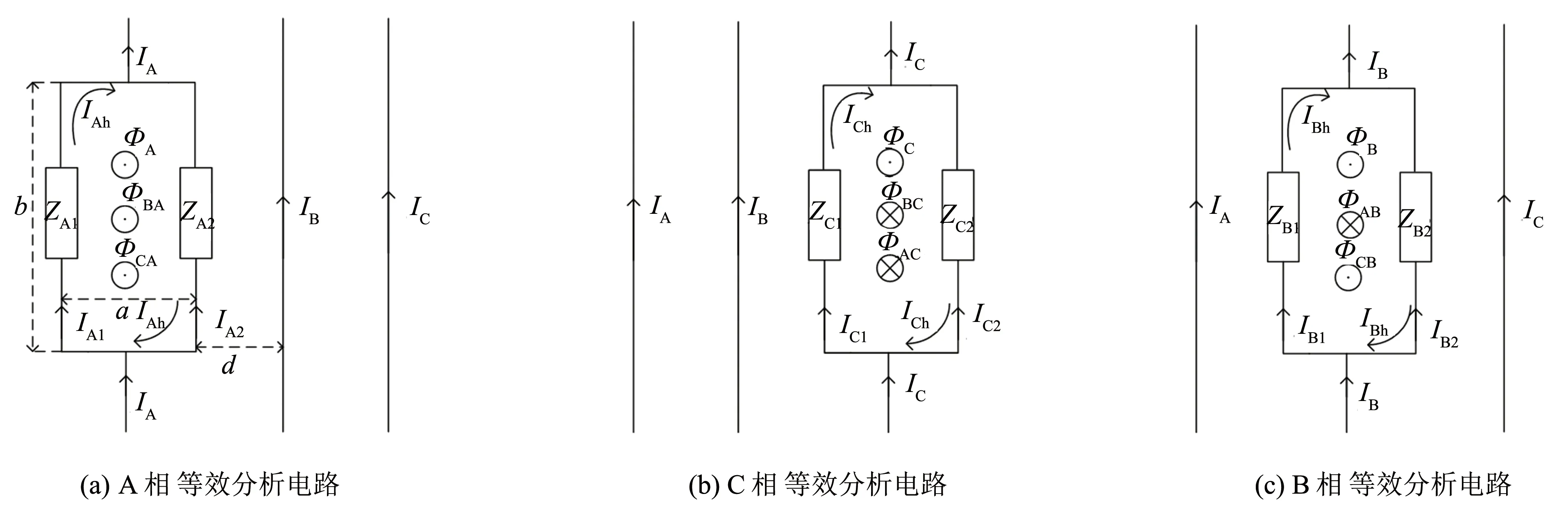
图2 三相并联型接触器触头回路分析等效电路Fig.2 Equivalent circuit of contact circuit of three-phase parallel contactor

图2(a)中，由于接触器触头通常等距离分布，在实际模型中长度d为长度a的1.5倍，C相中心线距离A2支路接触器距离为长度a的3.5倍.ΦBA、ΦCA分别为B、 C两相电流在A相闭合回路中产生的磁通，IAh为A相环流. 环流的方向如图2所示. A相回路中的合成磁通为：

Φa=ΦBA+ΦCA+ΦA

(2)

式中:ΦA是A相并联支路电流自身产生磁通之和;Φa为A相回路总磁通，则A相环流为：

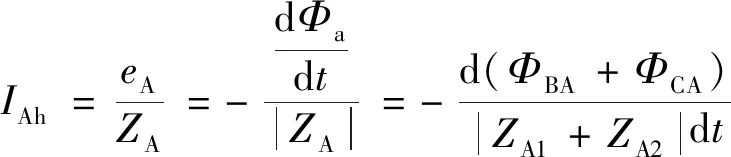
(3)

式中:eA为A相闭合回路中感应电动势. 进一步地，无限长导线在空间产生的磁场为：

(4)

为简化分析，假设一个参数k，结合式(2)～(4)，需满足以下条件：

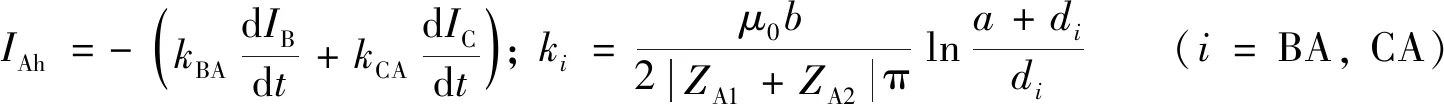
(5)

di表示各相中心线距离A2支路的距离. 则：

代入式(5)中计算得到：

式(6)中，Im为相电流幅值, 且k1>0,k2>0.

如图2所示，A相中各支路电流为：

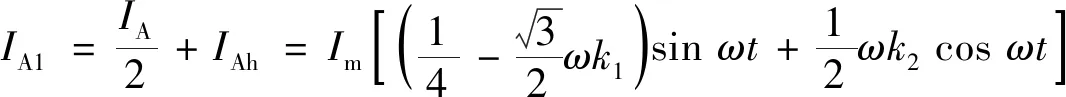
(7)

比较各支路电流幅值大小，可得：

(8)

显然, 由式(8)可知，IA2幅值大于IA1，A2支路接触器承受电流大于A1.

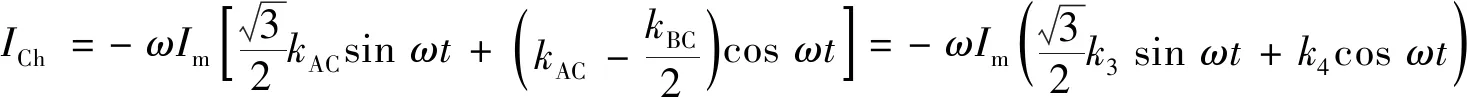
(9)

式中：k3> 0,k4< 0. 同式(7)结合环流方向可得, C相中各支路接触器电流为：

(10)

同理可得,IC1幅值大于IC2，即C相环流使C1支路接触器承受电流大于C2支路.

在对B相回路分析时，其等效电路如图2(c)所示. 其环流大小为：

(11)

同式(7)结合环流方向可得, B相中各支路电流为：

(12)

同理可得,IB1幅值大于IB2，即由于B相环流的存在，B1支路接触器承受电流大于B2.

综上分析可得, 当并联型接触器仅为单相运行时，在触头阻抗大小默认相同的情况下，其电流分配为均匀分配. 三相并联运行且相序为ABC时，各个支路其电流及环流关系为：

|IA2|>|IA1|, |IB1|>|IB2|, |IC1|>|IC2|; |IBh|>|IAh|>|ICh|

(13)

对各支路电流幅值进一步计算对比，可以得到B相各支路电流幅值相差最大，B相支路电流分配不均匀程度最为严重，而A相各支路接触器承受电流差异较小； 环流并未改变各支路电流频率，其频率与干路电流保持一致； 环流大小主要由电流等级和阻抗大小决定，与相位无关.

2 仿真验证及结果分析

2.1 仿真模型

在Maxwell中建立单相和三相并联型接触器触头3D模型，如图3所示. 将激励设置为外电路导入，利用Simplorer软件构建外电路，联合仿真电路模型如图4所示. 图中电阻值设置为与接触器触头的等效电阻相当. 电流源设置为50 Hz的正弦交流电源，其幅值可自定义设置.

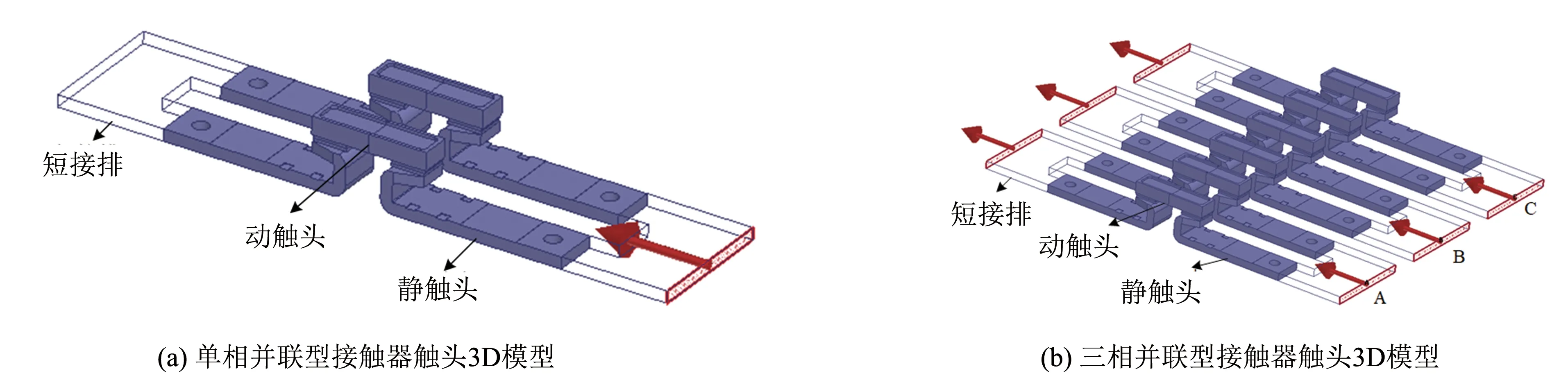
图3 并联型接触器触头3D模型Fig.3 3D model of parallel contactor contacts

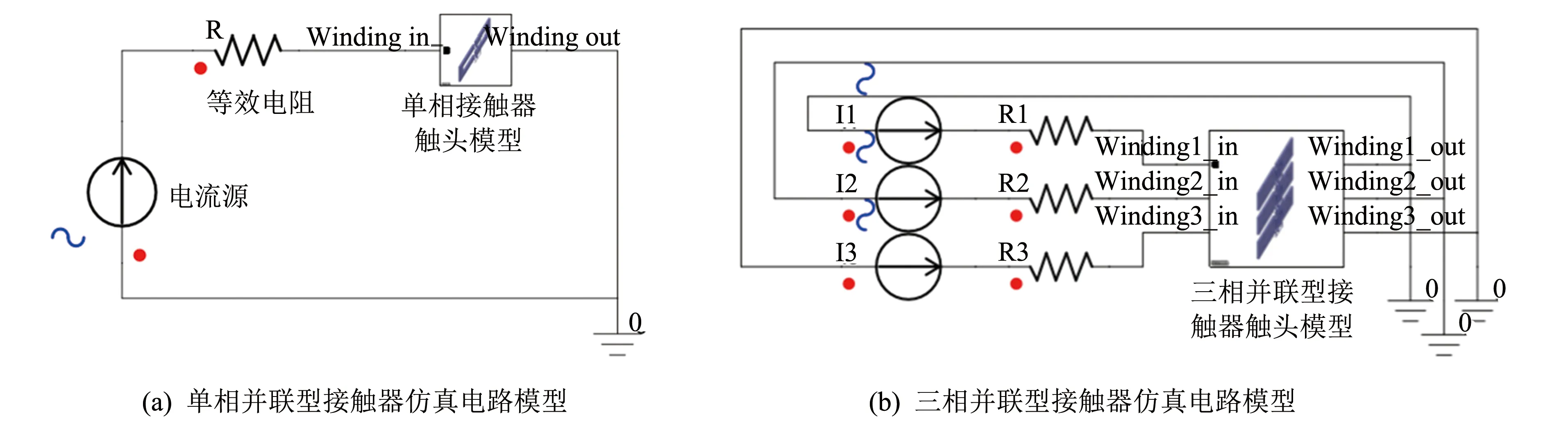
图4 并联型接触器仿真电路模型Fig.4 Simulation circuit model of parallel contactor

2.2 仿真结果分析

1.26 kA电流等级单相并联型接触器电流分布仿真结果如图5所示. 波形表明两个并联支路中电流波形完全重合，其幅值与相位均相同，电流分布为均匀分配，即各支路接触器承受电流相同且均为干路电流的一半，该结果与文中1.1小节分析结果保持一致.

1.26 kA电流等级三相并联型接触器仿真结果如图6所示. 其中各支路电流标号与图2保持一致. 从图中可见，电流幅值关系为：IA2>IA1,IB1>IB2,IC1>IC2，各相环流幅值大小仿真结果为：IBh>IAh>ICh. 电流频率并未改变，仿真结果均与式(13)完全吻合. 各支路电流大小统计如表1所示，结合图6可以看出, B相各支路电流相差最大，而A相最小，这与1.2小节分析结果保持一致.

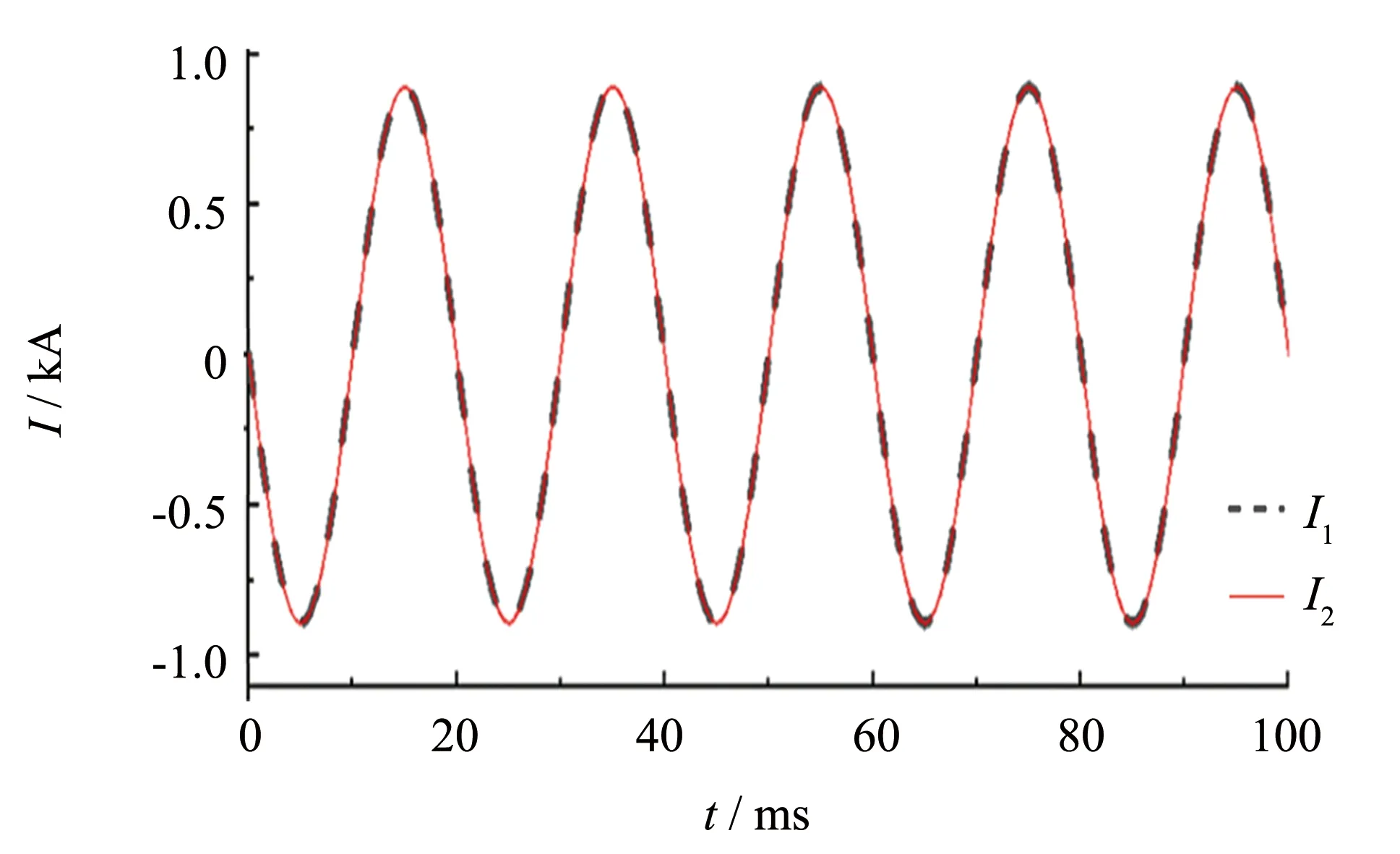
图5 单相并联型接触器触头电流分布Fig.5 Contact current distribution of single-phase parallel contactor

图6 三相并联型接触器触头电流分布Fig.6 Contact current distribution of three-phase parallel contactor

表1 并联型接触器电流分布及环流大小

3 并联型接触器电流分布影响因素分析

3.1 电流等级因素及扩容系数推导

将电流源设置不同电流等级，其他参数相同，电流等级为1.05 kA的仿真结果如图7所示. 与图6中1.26 kA电流分布波形对比，可以看出改变电流等级不影响各支路电流相位关系，幅值均按比例同步降低，取B相并联支路电流作为分析, 可以得到比例为：

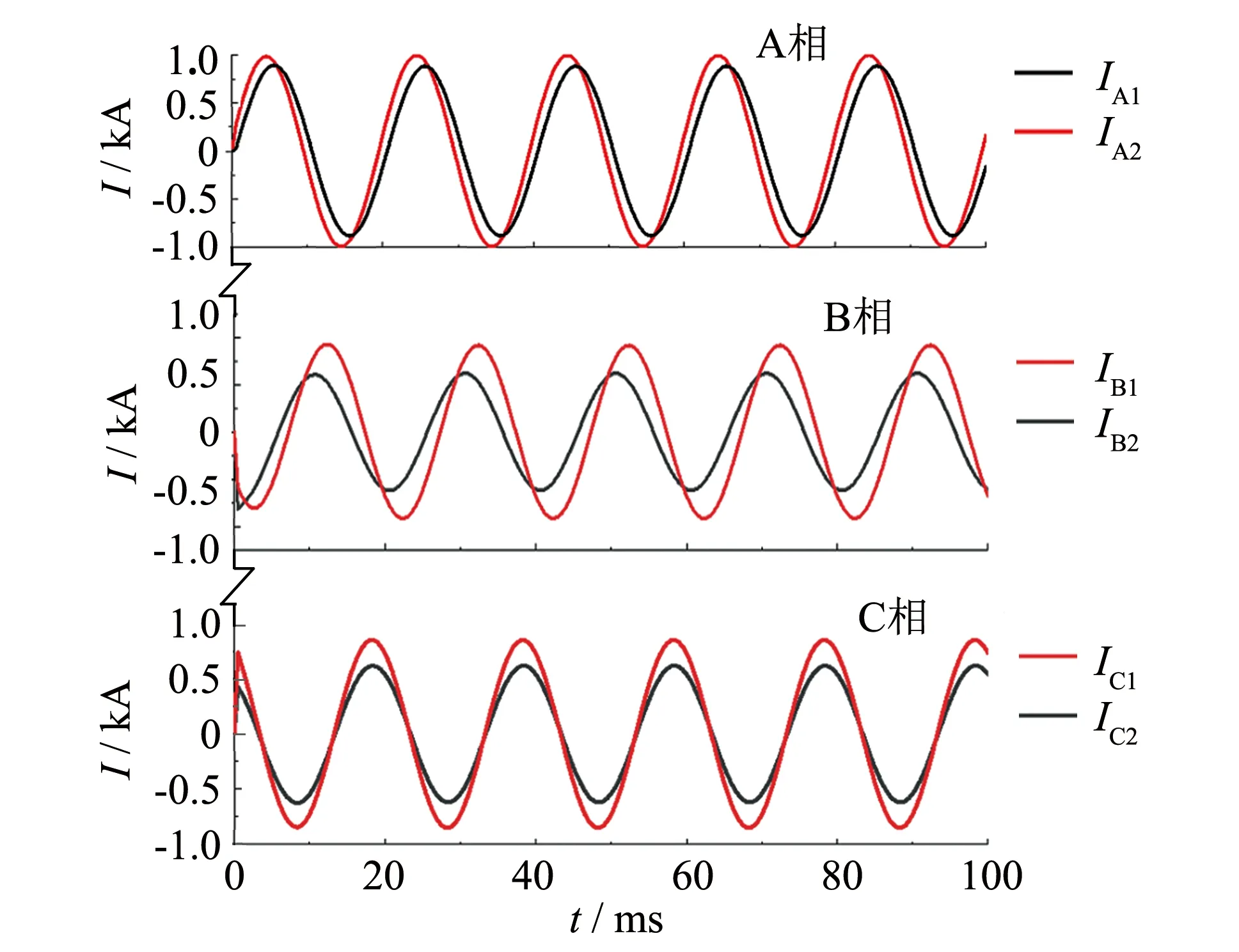
图7 1.05 kA电流等级触头电流分布Fig.7 Contact current distribution at 1.05 kA

选取多组电流等级进行仿真对比，其结果如表2所示. 仿真结果表明, 环流大小以及支路电流正比于电流等级，且比例为电流等级之比. 根据该规律进行扩容系数推导，按照承受电流最高的一支路接触器其通流容量不应超过额定值，可得：

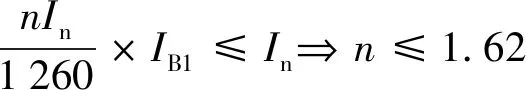
(14)

式中:n为扩容系数；In为接触器额定电流. 按照式(14)计算得到扩容系数最大值约为1.62，这与目前市场现有产品的扩容系数及论文研究结论基本符合.

表2 不同电流等级下IB1及IBh大小

3.2 频率因素

根据式(6)可得，环流与频率成正比，与阻抗成反比，而接触器阻抗同样受电源频率影响，因此可得不同频率下环流大小之比小于频率之比. 为验证该分析的正确性，将电流源频率改为60 Hz，其他参数不作变化，其仿真结果如图8所示.

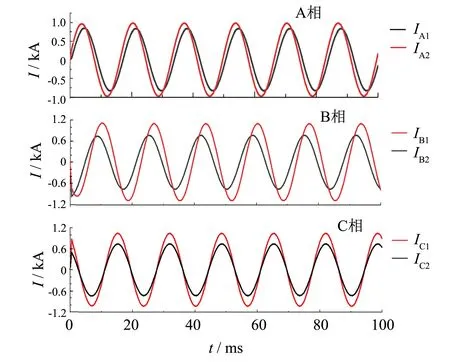
图8 频率为60 Hz下触头电流分布Fig.8 Contact current distribution at 60 Hz

从图中可知, 各支路电流大小关系仍为：IA2>IA1,IB1>IB2,IC1>IC2. 表3为电流源频率为50 Hz和60 Hz下的三相并联型接触器各相回路环流有效值统计结果. 电源频率为60 Hz时，各相环流有效值均大于50 Hz时的各相环流，并且可以得到：

即环流大小仍与频率成正比，但由于接触器阻抗同时会受频率影响，其比例将小于频率之比.

表3 不同频率下并联型接触器各相回路环流大小

3.3 相位因素

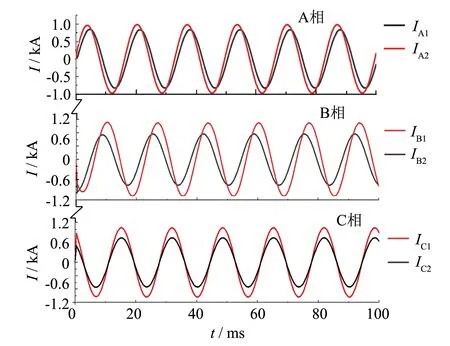
图9 初始相位90°下触头电流分布Fig.9 Contact current distribution at initial phase 90°

设定不同电流初始相位，以A相初始相位为90°的电流分布波形作说明. 如图9所示，在初始相位为90°情况下，三相并联型接触器各支路电流分布与图6结果相同. 表4为不同初始相位、 电流等级为1.26 kA且频率为50 Hz条件下的B相回路电流及环流大小. 从表中可以看出, 初始相位对三相并联型接触器的触头电流分布不会造成影响.

表4 不同初始相位下IB1及IBh值

4 结语

通过对并联型接触器的电路理论分析，得出其电流分布大小数学关系. 采用Maxwell与Simplorer软件构建并联型接触器触头联合仿真模型，所得仿真结果与理论分析结果保持一致. 最后, 研究了不同参数对并联型接触器分布特性的影响，可以得到以下结论.

1) 在阻抗参数相同的情况下，单相并联型接触器运行过程中电流均匀分配，各支路接触器承受电流相同. 而三相并联型接触器各支路电流则存在较大差异，可以判断造成三相并联型接触器降容使用是由交变磁场产生的回路环流引起的.

2) 由于环流的存在，使得在相序为ABC情况下, 三相并联接触器的电流分布大小关系为：IA2>IA1,IB1>IB2,IC1>IC2. 并且同相内各支路电流相位会发生改变.

3) 环流大小与电流等级、 频率成正比，与合闸初始相位无关. 不同电流等级的环流大小比例为电流等级之比，不同频率的环流大小例小于频率之比，初始相位不影响并联型接触器电流分布.

4) 根据仿真结果所得规律，进而推导得到三相并联型接触器的扩容系数约为1.62，与现有市场产品扩容系数及论文研究结论基本符合.