关联色噪声对具有免疫监视下肿瘤细胞生长系统稳定性和瞬态性质的影响

王国威,付 燕

(1.南昌工学院教育学院，南昌 330108;2.豫章师范学院数学与计算机学院，南昌 330108)

现代社会恶性肿瘤发病率逐年升高，且医治困难，导致大量病患及其家庭深受其害.肿瘤是由多种因素长期综合作用引起的一种复杂生物现象，它严重威胁人类健康[1-3].在医学及生物领域以外，物理、化学及数学等不同学科分支的科学家，都在各自专业领域研究肿瘤的生长规律和发病机理，以期探求建立合理有效的预防和治疗肿瘤的理论[4].近几十年来，各种描述肿瘤生长的数学物理模型不断出现，如Logistic模型、Gomperztion模型、自限制模型和Eden模型等[5-6]，并且有大量的研究者讨论噪声对肿瘤细胞生长过程的影响.王参军等[1]研究了受色高斯噪声驱动的肿瘤细胞增长系统的瞬态性质；别梦杰等[3]在免疫监视的肿瘤生长动力学模型中引入关联乘性白噪声，并考虑抗肿瘤体系的免疫系统激活阈值存在差异，对肿瘤细胞动力学生长方程进行数值仿真计算；邢菲等[4]研究了关联色噪声对肿瘤细胞生长的影响；钟伟荣等[5]在肿瘤生长模型中引入加性和乘性关联噪声，通过求解其对应的Fokker-Planck方程，揭示乘性噪声对肿瘤生长规律有分化作用；韩立波[6]将延时效应引入到肿瘤生长过程中，对色关联噪声驱动下具有线性延时的生长模型进行研究.

在实际情况下，肿瘤细胞的生长过程中总会受到一些随机因素(如温度、放射治疗、化疗、药物等)的影响，而且肿瘤的出现和生长是肿瘤与免疫系统二者之间非常复杂的相互作用结果，这种作用极可能是非线性和时变的[7-12].鉴于肿瘤细胞生长过程的复杂性，更多的研究者开始探讨从更全面、更高维度的二维捕食者—食饵模型或者具有催化Michaelis-Menten反应模型出发，力求找到一个更加接近肿瘤细胞生长过程且具备免疫监视的动力学模型.Ping Han等[7]讨论交叉相关噪声下免疫监测的肿瘤生长模型最可能的动力学特性；Alessandro Fiasconaro等[8]研究一种描述宿主机体免疫监视情况下肿瘤生长的数学模型；Kang-Kang Wang等[9]研究受相关乘法和加性噪声影响肿瘤生长系统的随机共振；R.Lefever等[10]发现噪声的影响可以有利于肿瘤的排斥反应，细胞毒性活性的波动和复制率的波动，且噪声效应可以提高免疫防御机制的效率；Alessandro Fiasconaro等[11]探究一个遵循通用的Michaelis-Menten动力学酶反应的随机系统的统计性质；Ochab-Marcinek等人和Fiasconaro等[12]人考察噪声对免疫监视下的肿瘤在两稳态势垒间的迁移率及噪声对肿瘤凋亡的影响；Koebel等[13]利用适应性免疫监视治疗让肿瘤细胞处于休眠状态而使得肿瘤有望变成可控的慢性病.这些研究从随机统计的角度定量地分析肿瘤细胞生长的动力学特性，相关结论不仅让肿瘤患者对肿瘤的恐惧观念和悲观认识发生变化，也为肿瘤临床诊断方式及治疗策略增添了新的方法和思路.

文章从具有催化作用的Michaelis-Menten反应[7-8]出发，得到一种更全面的具有免疫监视下肿瘤生长系统中肿瘤细胞数目随时间的随机一维演化朗之万方程[14]，考虑关联色噪声对模型的修正，利用线性化近似方法和最快下降法[15]，推导计算系统的稳态概率分布函数[16]和平均首次通过时间(平均首通时间)的解析表达式，并分析噪声对系统稳定性和瞬态性质的影响[17]，以期通过讨论从而促进对肿瘤的生长规律和发病机理进一步的研究，探求建立合理有效的预防和治疗肿瘤的理论，为肿瘤临床诊断及治疗提供新的理论基础.

1 模型构建

1.1 朗之万方程

机体的免疫系统不仅能够监视组织细胞的恶性演变，还能够杀死一定的肿瘤细胞.Lefever和Garay[10]运用酶促反应对免疫监控下的肿瘤细胞的增长过程进行研究，使用动力学方程的不同定态来暗示正常组织与癌组织以及它们之间彼此互相的转变，并且提出了肿瘤免疫监视模型[7，10-11，14-15].受免疫细胞侵入的肿瘤细胞增长模型可以用下面的具有催化作用的Michaelis-Menten反应来表示：

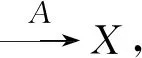
(1)

(2)

(3)

其中，X、Y、Z和P分别表示肿瘤细胞、免疫细胞、肿瘤细胞和免疫细胞的化合物、死亡或无复制能力的肿瘤细胞.符号A表示正常细胞的转化率，λ表示肿瘤细胞的复制率，κ1表示免疫细胞绑定癌细胞的绑定率，κ2表示化合物Z的分解率.

根据Michaelis-Menten理论[7-11]，可以将上述方程转化为单变量系统，则肿瘤细胞数目随时间的演化方程可以简化为下面的朗之万方程(LE)[12，18]:

(4)

式中，x表示肿瘤细胞的个数，α和β均是与肿瘤细胞出生率相关的的参量，β(≥0)被称为特异性免疫系数[19].

经过计算，系统的确定论势函数[20]的表达式如下：

(5)

方程(4)是一个确定性的LE，由于个体遗传、行为、能力的不同，或者治疗方法(如手术、化疗和放疗)而导致肿瘤细胞的生长出现随机性[21]，以乘性噪声的形式影响β，即β→β+ξ(t)；同时，考虑环境的波动对出生率的影响，例如温度、氧气和养分供应以及宿主的免疫状态等，属于系统外噪声[22]，以加性噪声的形式加入系统，即α→α+η(t).因此，可以得到描述肿瘤细胞生长的随机LE[23]：

(6)

式中，ξ(t)和η(t)均为零均值的高斯色噪声，且它们的统计性质[24]如下：

〈ξ(t)〉=〈η(t)〉=0,

(7)

(8)

(9)

〈ξ(t)η(t′)〉=〈η(t)ξ(t′)〉=

(10)

其中，D和Q表示噪声强度，λ表示噪声间的关联强度[25]，τ1、τ2和τ3分别表示加性噪声、乘性噪声的自关联时间和噪声间的互关联时间[26]，t为时间.

按照文献[25]的方法，将LE(6)式进行等价变换，可改写为如下形式[27]：

(11)

其中，

对式(11)进行系综平均后，计算出相应的福克-普朗克方程(FPE)[28]：

(12)

其中，P(x，t)代表系统的概率分布函数[29]，即在t时刻系统的肿瘤细胞数量出现在x时对应的概率，且有：

(13)

(14)

1.2 稳态概率分布函数

在稳态条件下，求得FPE的稳态解为[30]：

(15)

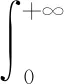
ln|A0x2+A1x+A0|+

(16)

其中，

且考虑自关联时间和互关联时间相同，即有τ1=τ2=τ3=τ.

1.3 平均首次通过时间

从非线性学科的角度看，平均首通时间[31]是度量随机系统瞬态性质的重要物理量:为系统从一个势阱的稳态穿越势函数的势垒到达另一个势阱的稳态所花费时间的平均值[32].根据最快下降法和平均首通时间的定义，计算得到从两个不同方向、分别由系统的稳定态转化到非稳定态的平均首通时间的精确表达式[33-34]：

(17)

(18)

上述两式中，B(x)由式(14)给出，x±表示系统的两个稳定态，xu表示系统的非稳定态；U(x)为系统的修正势函数[35]，由公式(16)给出；V(x)由公式(5)给出，被定义为系统的确定性势函数[36-37].

2 系统的稳态性质和瞬态性质

2.1 确定论系统的稳定性分析

按照式(5)和式(16)，系统的确定性势函数[38]和修正势函数[39-40]如图1所示.根据系统确定论势函数方程式(5)，系统的稳定点和不稳定点(也称为亚稳态点)分布[41]有以下几种情况：

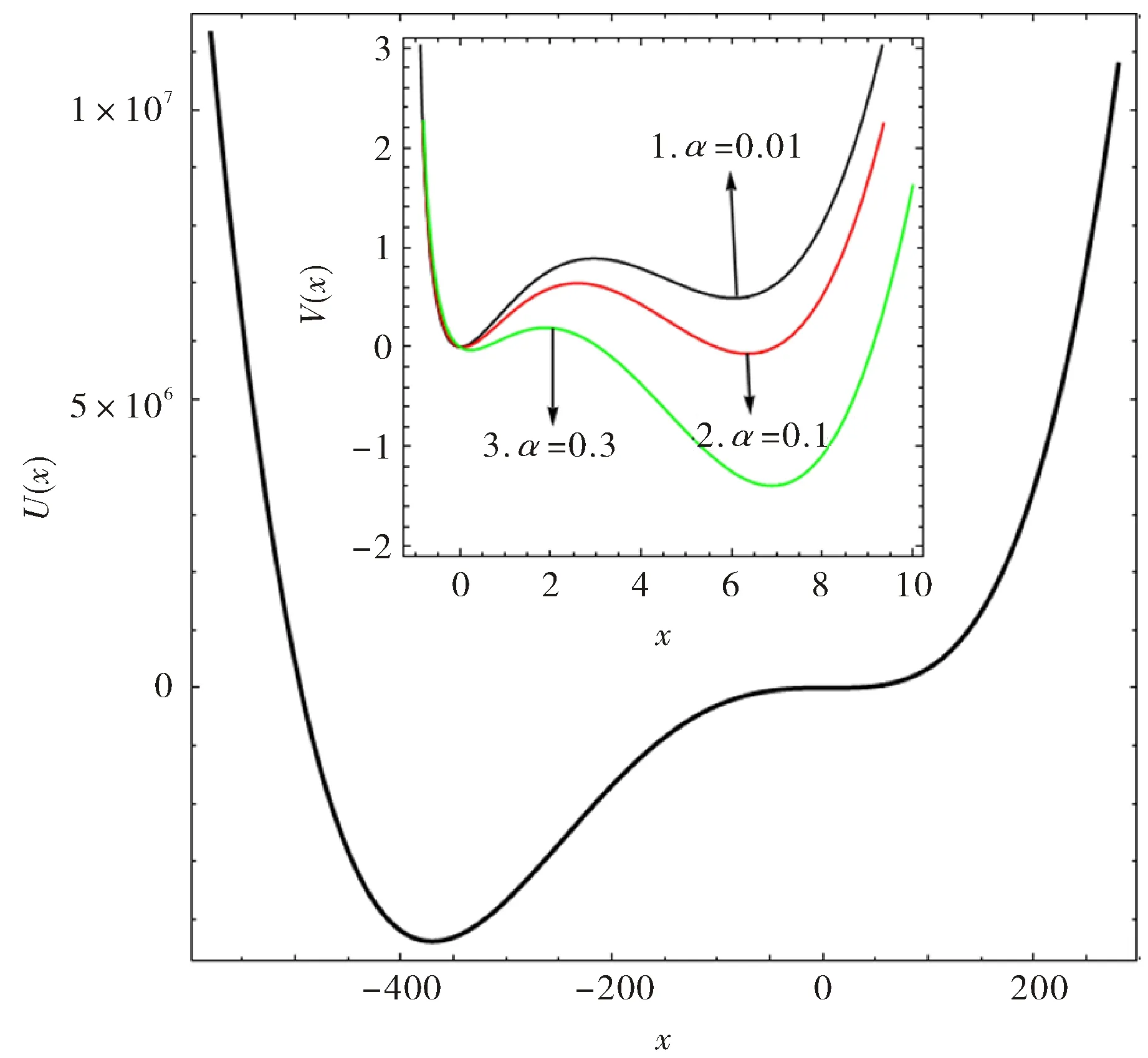
图1 确定论势函数V(x)和修正势函数U(x)Fig.1 Deterministic potential function V(x) and fixed potential function U(x) of the system

为满足研究的要求，参数选取范围需满足上述第2点要求[42-44].图1表明，α对系统的确定论势函数V(x)会产生一定影响：不仅影响系统其稳定点(亚稳点)的位置，还影响该稳定点(亚稳点)对应势函数的大小[45-46].对于一般分析力学中，在讨论理想、完整、有势系统时，其势函数与广义速度无关，被称为普通势.广义势函数则是一个推广了的概念，被用来讨论势函数与广义速度有关的情况.系统的修正势函数U(x)，也称为广义势函数，当修正势函数的取值为U(x)=0时，则可得到系统的2个稳态解和1个非稳态解，如图1.在已有的研究中[41，47-48]系统参数取值为α=0，β=2.8，θ=0.1，但是，α=0意味着忽略了对肿瘤细胞出生率存在的影响，因此导致系统模型和实际情况出现一定偏差.从图1可以看出，α对系统的性质会产生一定影响，因此不可忽略，故对参数进行优化[49]，选取α≠0，β=2.8，θ=0.1，确保系统模型与真实的肿瘤细胞生长过程更加接近.

2.2 噪声对稳态性质的影响

根据稳态概率分布函数的公式，绘制出其随乘性噪声强度D变化的曲线，如图2所示.图2表明，随着D的增加，Pst(x)可能呈现出2个或3个极值：当D=0.01和0.03时，曲线有1个极小值和一个极大值；但是当D继续增加至0.06和0.09时，在极小值的左边又产生1个极大值.而且，随着D的增加，左边的极大值愈发明显且其峰值所在位置逐渐向右移动.由此可见，乘性噪声强度D的改变，可以改变肿瘤细胞数概率分布函数Pst(x)的结构，导致系统产生由多极值向单极值的结构转换，或导致系统产生类相变，意味着由遗传、基因和个体差异导致的内噪声可以影响肿瘤细胞的生长.

θ=0.1，β=2.8，α=3，λ=0.5，Q=0.09，τ=0.1图2 乘性噪声强度D对稳态概率分布函数的影响Fig.2 Effect of multiplicative noise intensity on steady-state probability distribution function

当改变加性噪声强度Q的时候，Pst(x)曲线整体的走势大致和改变乘性噪声时的图像一致，图像同样出现3个极值和2个极值的转变.不同之处在于，当改变加性噪声强度Q的时候，Pst(x)在较小噪声作用时呈现出3个极值点，但是随着噪声增大，靠近x=0处的极值消失.另外一个比较明显的变化就是，噪声强度越大，稳态概率分布函数图像右边的峰值越高.综合图2和图3分析，从概率分布意义上可以看出，乘性噪声和加性噪声对肿瘤细胞生长的影响，具有不同的作用.

图4给出稳态概率分布函数随噪声间关联强度λ和关联时间τ变化的图像.图4表明，两图中Pst(x)图像的大致结构基本一致，且噪声间关联强度λ的变化对稳态概率分布函数的影响较小.值得注意的是，当噪声间关联时间τ变大时，图像在x更大的位置的峰值变大，意味着肿瘤细胞在数量更大的地方出现的概率变大，系统的稳定性得到加强.上述分析反映出在选定的参数范围内，较大的噪声间关联时间有利于使肿瘤细胞生长系统趋近于更稳定的状态.

2.3 噪声对瞬态性质的影响

为研究系统的瞬态性质，图5～8绘制系统的平均首次通过时间T(xu→x±)的图像.因为系统有1个非稳定点xu和2个稳定点x±，因此考虑的平均首次通过时间包含从亚稳定xu跃迁到稳定态x±2个方向，故在图像中分别考虑T+(xu→x+)和T-(xu→x-)作为对比.图5表明，T+(xu→x+)是乘性噪声强度D的单调增函数，意味着随着噪声强度D的增加，系统的平均首次通过时间逐渐增加.而且，当噪声强度固定时，随着噪声间关联强度λ的增加，平均首次通过时间有变小的趋势.上述结果表明，在给定参数范围内，适当增加乘性噪声强度D，有利于肿瘤细胞生长；且增加噪声间关联强度λ，有利于肿瘤细胞从衰减状态向生长状态转变.但是，T-(xu→x-)却是乘性噪声强度D的单调减函数，且噪声强度不宜过大.由此可以看出，当肿瘤细胞处于另外一个稳定态时，外界环境的波动会导致肿瘤细胞平均首次通过时间迅速减小为0，意味着系统出现相变，肿瘤细胞由稳定生长状态趋近于灭绝态，这对肿瘤治疗有一定指导意义.

θ=0.1，β=2.8，α=3，λ=0.5，D=0.09，τ=0.1图3 加性噪声强度Q对稳态概率分布函数的影响Fig.3 Effect of additive noise intensity on steady-state probability distribution function

(a)θ=0.1，β=2.8，α=3，D=0.01，Q=0.09，τ=0.1 (b)θ=0.1，β=2.8，α=3，D=0.01，Q=0.09，λ=0.5图4 噪声间关联强度λ和关联时间τ对稳态概率分布函数的影响Fig.4 The influence of noise correlation intensity and correlation time on steady-state probability distribution function

图6表明，当改变加性噪声强度Q时，平均首次通过时间T+(xu→x+)和T-(xu→x-)表现出不同的变化趋势：后者是噪声强度Q的单调减函数，而前者不是，前者的图像出现一个类似“共振峰”的极大值.另外，随着乘性噪声强度的增加，峰值所在位置逐渐向右移动，且噪声强度越大，峰值高度越大.峰值越低意味着系统的平均首次通过时间变小，反映出肿瘤细胞的平均灭绝时间变小，系统稳定性越低，肿瘤细胞较快走向衰落期，这对肿瘤治疗是具有积极意义的.当系统处于另一个稳定态x-时，随着加性噪声强度Q的增加，系统的平均首次通过时间以较快的速度单调减小.

(a)θ=0.1，β=2.8，α=3，Q=0.09，τ=0.01 (b)θ=0.1，β=2.8，α=3，Q=0.05，τ=0.01图5 平均首通时间作为噪声强度的函数随关联强度变化Fig.5 The mean first-passage time versus intensity of the noise under different intensity of correlation

(a)θ=0.1，β=2.8，α=3，λ=0.5，τ=0.01 (b)θ=0.1，β=2.8，α=3，λ=0.5，τ=0.01图6 平均首通时间作为噪声强度的函数Fig.6 The mean first-passage time versus intensity of the noise

图7表明，T+(xu→x+)随噪声间关联时间τ变化时，表现出单调递减和“共振峰”两种状态，由此可知，合适大小的噪声强度，诱导系统的平均首次通过时间出现“极大值”，系统稳定性最强，肿瘤细胞处于生长繁殖期，不利于临床上对肿瘤疾病的治疗.T-(xu→x-)图像随噪声关联时间τ的变化呈现出单峰值样态，意味着在给定的噪声间关联强度下，一定大小的关联时间会使系统的平均首通时间最大，肿瘤细胞不易走向衰减期.另外，噪声间关联强度的增加，会导致峰值高度的增加，表明适当降低噪声间关联强度，可以使肿瘤细胞较快地趋近于衰减期.

图8给出系统处于稳定态x-和非稳定态xu之间的平均首通时间随加性噪声强度Q和噪声间关联强度λ之间的图像.图8表明，T+(xu→x+)随λ的变化出现类似于“共振峰”的极大值，且随着噪声强度Q的减小，其峰值所在位置逐渐向右移动，但是在移动的过程中，其峰值的大小基本不变.另外，在小噪声情况下，T-(xu→x-)是λ的单调减函数.当噪声间关联强度λ增加时，平均首通时间也是快速趋近于0.

(a)θ=0.1，β=2.8，α=3，λ=0.5，Q=0.09 (b)θ=0.1，β=2.8，α=3，Q=0.05，D=0.09图7 平均首通时间作为关联时间的函数Fig.7 The mean first-passage time versus the correlation time of noise

(a)θ=0.1，β=2.8，α=3，D=0.09，τ=0.01 (b)θ=0.1，β=2.8，α=3，D=0.09，τ=0.01图8 平均首通时间作为噪声强度和关联强度的函数Fig.8 The mean first-passage time versus the intensity and intensity of correlation

3 结论与总结

研究结果表明：1) 当改变噪声强度D和Q时，可以改变肿瘤细胞数概率分布函数Pst(x)的结构，导致系统产生多极值和单极值之间的结构转换，系统产生类相变；2)T+(xu→x+)是乘性噪声强度D的单调增函数，T-(xu→x-)却是乘性噪声强度D的单调减函数；3)T+(xu→x+)随加性噪声强度Q变化的图像出现一个类似“共振峰”的极大值，而T-(xu→x-)是关于Q的减函数；4)T+(xu→x+)随噪声间关联时间τ变化时，表现出单调递减和“共振峰”两种状态的转换，而T-(xu→x-)的图像随噪声关联时间τ的变化呈现出单峰值样态；5)T+(xu→x+)随λ的变化出现类似于“共振峰”的极大值，T-(xu→x-)是λ的单调减函数.通过理论分析和数值模拟，文章研究一种改进的具有免疫监视的肿瘤细胞生长系统的定态和瞬态性质等特性.掌握肿瘤细胞的生长动力学特性，不仅能够为临床上肿瘤细胞生长和抑制提供一定理论基础，而且还能为临床医学上肿瘤检测和治疗提供理论指导，对控制和治疗肿瘤疾病有一定的指导意义.