中国期货市场的流动性溢价研究——来自异常波动条件下的证据

刘庆柏 时 琛 王川杰

(复旦大学 大数据学院，上海 200433；复旦大学 经济学院，上海 200433)

一、 引 言

2020年10月9日，经国务院批准，中国证监会决定成立广州期货交易所筹备组，启动广州期货交易所的筹建工作。这是证监会在新形势下加快推进金融市场开放、加大商品期货市场开放力度和多元发展的重大举措。

期货市场具有价格发现和套期保值两大基本功能。就套期保值而言，通过购买期货合约转移价格波动风险，如玉米、大豆等农产品价格受气候因素影响很大，通过期货合同提前锁定价格可以规避价格频繁波动的风险。就价格发现而言，通过期货市场提前发现价格，掌握大宗商品的定价权。我国是全球第一贸易大国，但很多大宗商品的定价权并不掌握在自己手上，距离贸易强国还有不小的差距，而通过大宗商品等期货交易，可以一定程度上争夺国际贸易的定价权。

自1990年郑州商品交易所成立以来，中国期货市场经历近30年的发展，已有了长足进步，其价格发现和套期保值等功能相对完善。然而随着资本市场深化改革和对外开放的力度加强，以及疫情等极端风险的存在，期货市场仍然存在暴涨暴跌的现象。例如，2016年11月15日，商品期货市场再现集体跳水，螺纹钢、铁矿石、玻璃跌停，PTA跌逾5%，豆油跌超4%，菜油跌超3%，领头羊焦煤焦炭也分别有6%、8%的跌幅(news.hexun.com, 2016)；2017年8月7日，螺纹钢主力合约1710强势涨停，盘中触及4101元/吨，创近四年半以来新高，而在螺纹钢涨停不久后，PTA一度闪崩近200点(news.hexun.com, 2017)；2018年11月14日，上期所原油期货夜盘跌停，日内跌逾5%，原油1902、1812、1901合约全部跌停(finance.ifeng.com，2018)；2020年3月16日至18日，上期所白银主力合约连续大跌，三个交易日共跌去20%，盘中跌破3000元(finance.eastmoney.com，2020)。我们常称以上所列的期货市场剧烈变化为异常波动，其具有发生率低、无法预期、影响力大、难以量化和转移等特点。

不同于正常波动(1)本文所提及的正常波动是与异常波动相对的概念。对整个资本市场而言，除异常波动情况以外，其他波动均称为正常波动。，异常波动具有更丰富的信息内涵(Yoon and Byun, 2009(2)S-J Yoon, S J. Byun, “Is Volatility Risk Priced in the KOSPI 200 Index Options Market?” Journal of Futures Markets 29.9 (2009): 797-825.；Albuquerque, 2012(3)R. Albuquerque, “Skewness in Stock Returns: Reconciling the Evidence on Firm Versus Aggregate Returns,” Review of Financial Studies 25. 5 (2012): 1630-1673.; Diavatopoulos et al. 2012(4)D. Diavatopoulos, J. S. Doran, A. Fodor, D. R. Peterson, “The Information Content of Implied Skewness and Kurtosis Changes Prior to Earnings Announcements for Stock and Option Returns,” Journal of Banking and Finance 36 (2012): 786-802.; Neuberger, 2012(5)A. Neuberger, “Realized Skewness,” Review of Financial Studies 25.11 (2012): 3423-3455.; Conrad et al., 2013(6)J. Conrad, R. F. Dittmar, E. Ghysels, “Ex Ante Skewness and Expected Stock Returns,” Journal of Finance 68.1 (2013): 85-124.)。流动性作为微观结构的核心要素，异常波动会导致市场在交易规模、市场主体等方面具有不同特征，这会综合反映在市场流动性上(丁重和邓可斌，2012(7)丁重、邓可斌：《流动性因素与中国股市的技术创新信息反馈——基于股价特质波动的实证》，《产业经济研究》2012年第4期。；Liu et al., 2016(8)Q. Liu, R. Hua, Y. An Y, “Determinants and Information Content of Intraday Bid-ask Spreads: Evidence from Chinese Commodity Futures Markets,” Pacific-Basin Finance Journal 38 (2016): 135-148.)。同时，许多学者研究发现，处于异常波动状态的资本市场会呈现出较大差异的市场特征(Jiang et al.，2011(9)G. J. Jiang, I. Lo, A. Verdelan, “Information Shocks, Liquidity Shocks, Jumps, and Price Discovery: Evidence from The U.S. Treasury Market,” Journal of Financial and Quantitative Analysis 46. 2 (2011): 527-551.；Dungey and Hvozdyk，2012(10)M. Dungey, L. Hvozdyk, “Cojumping: Evidence from the US Treasury Bond and Futures Markets,” Journal of Banking & Finance 36 (2012): 1563-1575.; Fernando et al.，2012(11)C. S. Fernando, A. D. May, W. L. Megginson, “The Value of Investment Banking Relationships: Evidence from the Collapse of Lehman Brothers,” Journal of Finance 33.1 (2012): 235-270.)。并且，异常波动条件下的资本市场在流动性和溢价等方面也表现出极大的差异性(朱垚，2013(12)朱垚：《极端波动条件下的中国商品期货市场流动性信息含量研究》，复旦大学硕士论文，2013年。；Acharya and Pedersen, 2005(13)V. Acharya, L. H. Pedersen, “Asset Pricing with Liquidity Risk,” Journal of Financial Economics 77 (2005): 375-410.；Todorov，2010(14)V. Todorov, “Variance Risk Premium Dynamics: The Role of Jumps,” Review of Financial Studies 23 (2010): 345-383.)。尽管差异被学者和市场所捕捉，但仍缺乏对市场在异常波动状态下流动性的研究。

目前，关于流动性溢价的研究也不少，研究对象主要是异常波动状态下的风险溢价。Wright and Zhou (2009)(15)J. H. Wright, H. Zhou, “Bond Risk Premia and Realized Jump Risk,” Journal of Banking and Finance 33 (2009): 2333-2345.研究发现，增加跳跃均值比增加期权隐含波动率和高频数据实际波动率使得债券市场收益率更易预测。Todorov and Bollerslev(2010)(16)V. Todorov, T. Bollerslev, “Jumps and Betas a New Framework for Disentangling and Estimating Systematic Risks,” Journal of Econometrics 157 (2010): 220-235.利用非连续的二次幂变差模型研究了风险溢价变量在解释隐含和现实波动性方面的动态特征，从理论上探索了跳跃的贝特值及其与连续贝特值之间的关系。此外，Wu(2019)(17)Y. Wu, “Asset Pricing with Extreme Liquidity Risk,” Journal of Empirical Finance 54 (2019): 143-165.将异常流动性风险嵌入经流动性调整的资本资产定价模型(CAPM)，并利用1973～2011年的股票面板数据给出了异常流动性风险的测度方法，给出了收益溢价证据，这一研究与朱垚(2013)的研究结果相一致。该研究成果进一步证明了经流动性调整后的资本资产定价模型中，证券的预期收益率不仅取决于预期流动性，还取决于证券收益率或流动性与市场收益率或流动性之间的协方差，在市场波动超过一定阈值时，市场会产生异常波动，进而引发剧烈下降。此外，Ruenzi et al.(2012)(18)S. Ruenzi, M. Ungeheuer, F. Weigert, “Extreme Downside Liquidity Risk,” Working paper, University of Mannheim, 2012.利用Copula函数捕捉到股票市场收益的较低尾部特征，发现市场预期收益能够反映异常波动条件下的流动性风险溢价。

以上研究多基于价格的考量，而实际上仍有很多文献针对于交易变量的分析。Gervais et al.(2011)(19)S. Gervais, R. Kaniel, D. Mingelgrin, “The High-Volume Return Premium,” Journal of Finance 57.3 (2011): 877-919.发现极端交易活动隐含了市场对股价未来的预期，在短期内具有较高成交量的股票在较长时间窗口内更易达到更高价格，即高成交量的收益率溢价。而在对衍生品市场的研究中，Broadie et al.(2007)(20)M. Broadie, M. Chernov, M. Johannes, “Model Specification and Risk Premia: Evidence from Futures Options,” Journal of Finance 62 (2007): 1453-1490.使用1987年至2003年间的标准普尔期货期权价格来估计扩散性和跳跃风险溢价。Chan and Feng(2012)(21)W. H. Chan, L. Feng, “Time-Varying Jump Risk Premia in Stock Index Futures Returns,” Journal of Futures Markets 32.7 (2012): 639-659.研究测试了与极端新闻事件或股指期货收益跳升相关的时变风险溢价的存在，并发现股指期货具有显著的跳跃风险溢价。Wang et al.(2013)(22)K. Wang, J. Liu, and Z. Liu, “Disentangling the Effect of Jumps on Systematic Risk Using a New Estimator of Integrated Co-Volatility,” Journal of Banking and Finance 13 (2013): 1777-1786提出了一种新的协波动估计量来分析价格跳跃对于系统性风险的影响，发现在控制对Beta估计有显著影响的跳跃变量以后，跳跃的影响在很大程度上取决于共同跳跃变量，但也存在证据表明异质性的跳跃会导致显著性的偏差。不同于如前所述的价格信息研究，Huang and Heian(2010)(23)Z. Huang, J. B. Heian, “Trading-volume Shocks and Stock Returns: an Empirical Analysis,” Journal of Financial Research 33.2 (2010): 153-177.从交易量角度研究了异常高交易量溢价现象，实证结果显示，以1962年至2005年为时间窗口，每周高交易量的风险溢价平均达到0.50%。以上研究为本文奠定了基础。虽然沈虹(2013)(24)沈虹：《基于综合流动性度量指标的中国期货市场流动性溢价研究》，《数理统计与管理》2013年第2期。等对中国期货市场的流动性溢价进行了初步研究，但对异常波动条件下的期货市场的流动性溢价研究尚相对缺乏。

针对现有研究中存在的问题，本文的主要内容和创新在于：从理论层面上，对异常波动条件下期货市场流动性溢价的研究将是基于流动性溢价的资产定价、投资组合和套利模型研究的重要内容，利用MRS-SGED模型进行分析也将丰富期货市场的金融计量学内容，并为研究在异常波动下期货市场的套利机制提供新视角；从实际层面上，尽管我国新冠肺炎疫情已处于可防可控状态，但国外疫情风险向国内金融市场的传导仍不可避免，同时我国加强资本市场对外开放，这都将显著增加我国期货市场异常波动的概率，本文研究成果将为投资者在现实情况下的套期保值等策略提供新思路。

二、 基于MRS-SGED的流动性溢价模型的建立

(一) 模型建立及异常波动状态概率计算

关于价格或收益率序列异常波动识别的模型有很多，本文采用的是Hamilton在1987年提出的马尔科夫体制转换(Markov Regime Switching，MRS)的识别方法。基于MRS-SGED的机制转化模型可以构建为：

rt=ust+εt

(1)

εt～SGED(0,σst，λst,kst)

(2)

st～Markov_process(2)

(3)

其中，rt表示资产的收益率序列，ust表示收益率均值，εt服从带偏度的广义误差分布(SGED)，σst、λst、kst分别表示带有状态变量st的波动率、偏度和峰度参数，状态变量服从马尔科夫过程。我们假设一共存在两种状态，对应状态1：st=1情况下的参数组合为(μ1,σ1,λ1,k1)，对应状态2：st=2下的参数组合为(μ2,σ2,λ2,k2)。我们假设在异常波动和正常波动两种情形下收益率均值、偏度和方差会同时发生显著变化。根据Panayiotis Theodossiou(2015)(25)P. Theodossiou, “Skewed Generalized Error Distribution of Financial Assets and Option Pricing,” Multinational Finance Journal 19.4(2015): 223-266.对于SGED的定义，我们可以得到rt在st=j下的概率密度函数。

进一步地，根据Hamilton(1987，1996)的研究，对模型的参数而言，用MSR模型最终计算出来的是时间序列在某一时期处于某一状态的概率，依据马尔科夫链的性质我们记t时刻st=j的概率为πj，即

P(St=j;Θ)=πj,j=1,2

(4)

那么根据全概率公式可以计算出rt在t时刻的无条件概率：

(5)

最后根据Bayes公式可以得到t时刻在已知观测值rt下的st=j的条件概率：

(6)

由于研究只包含异常和正常波动两种状态，延续Hamilton(1987)对美国经济周期的实证研究中以0.5作为分界点对两种状态的划分，当P(st=j|rt;Θ)大于0.5时我们认为当前所处的状态为第一种情形，反之认为处在第二种情形。

(二) 流动性变量的测度

相对买卖价差将采用与Cai et al. (2004)(26)C. X. Cai, R. Hudson, K. Kease, “Intra Day Bid-Ask Spreads, Trading Volume and Volatility: Recent Empirical Evidence from the London Stock Exchange,” Journal of Business Finance & Accounting 31. 5/6 (2004): 647-676.相一致的指标。具体而言，相对买卖价差公式为：

(7)

其中，Askt表示在t时刻卖方卖出所需要收到的对价，Bidt表示在t时刻买方买入愿意支付的对价。为计算买卖价差，本文以每半小时计算其平均值。该指标存在着未充分考虑交易规模的缺陷，所以我们将它用于直接刻画交易成本。

在对期货市场流动性产生决定性影响的变量中，收益率是其中之一，因此本文根据Brockman and Chung(2002)(27)P. Brockman, D. Y. Chung, “Commonality in Liquidity: Evidence from an Order-Driven Market Structure,” Journal of Financial Research 25.4 (2002): 521-539.的方法计算收益率：

Returnt=ln(pt/pt-1)

(8)

其中，pt为t时刻期货交易的收盘价格。

(三) 流动性溢价的建模

根据上文提到的异常波动的识别方法，如果MRS-SGED识别出的处于状态2下的条件概率大于0.5，记为P(st=2)≥0.5，我们认为此时期货市场处在异常波动(Abnormal Volatility, AV))状态；反之，我们认为处于正常波动(Normal Volatility, NV)状态，记为P(st=2)<0.5。据此，本文将建立两个模型：一个是不区分好坏消息下基于价格信息的流动性溢价模型；另一个是区分好坏消息下基于价格信息的流动性溢价模型。

首先，不区分好坏消息下基于价格信息的流动性溢价模型为：

(9)

其中，Returnt为t时刻的收益，Spreadt为t时刻的买卖价差。

其次，区分好坏消息下基于价格信息的流动性溢价模型为：

(10)

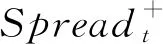
三、 异常波动下期货市场流动性的统计特征

(一) 数据选择

本文所研究的期货合约主要是三大商品期货交易所中交易最活跃的前五个品种，具体包括上海期货交易所(SFE)的铜(cu)、铝(al)、黄金(au)、锌(zn)和橡胶(ru)期货，郑州商品交易所(ZCE)的棉花(CF)、PTA(TA)、菜籽油(OI)、白糖(SR)和甲醇(MA)期货，以及大连商品交易所(DCE)的豆粕(m)、豆油(y)、玉米(c)、焦炭(j)和铁矿石(i)。由于中国商品期货合约指令订单簿对于行情统计具有非连续的特征(28)在买卖价差与订单数量的选择中，不同于做市商制度下的数据生成方式，指令驱动市场是以指令簿报价为基础的。在指令簿报价中，只要没有成交，报价者就不承担任何责任，因而，越远的报价越不可信(如买五和卖五)。因此，为避免可能存在的虚假报价，本文选择最近的买卖报价与订单数量，即选择买一和卖一的最优报价及其订单数量。，故本文整体上选择主力合约的半小时数据，并在每半小时内以一分钟为频率计算平均收益、流动性指标和高阶矩变量，其时间跨度为2013年1月1日～2017年12月31日(29)各个期货合约的具体交易时间是：8:55～9:00 为集合竞价时间；9:00～11:30 为上午交易时间；13:00～15:00 为下午交易时间，在本文中暂不考虑夜盘交易。。

这样选取的理由是：(1)虽然目前从交易所可得的期货高频交易数据最短间隔为半秒，以半秒为间隔提取出来的30分钟内收益率数据有3600个样本，在此基础上计算出来的高阶矩变量可以避免受到异常值的影响；但在本文中，我们不建议用如此高频率的数据。因为虽然样本量增加了，但是由于间隔时间过短，市场价格无法充分反映投资者的交易行为，因此收益率数据过于集中在0值附近。这样导致的结果是峰度指标过大，偏度指标无法得到充分体现，并且MRS模型的识别效果也会大幅度下降。(2)国内期货市场起步较晚，大部分文章中所选取的期货品种上市时间较短，而新型的金融产品在刚推出后往往需要一段时间的适应期(Gounaris and Akamavi，2005(30)S. Gounaris, & R. K. Akamavi, “Re-engineering Service Quality Process Mapping: E-Banking Process,” International Journal of Bank Marketing, 2005.；曾薇和陈收，2009(31)曾薇、陈收：《金融监管对金融产品创新影响研究新进展》，《经济学动态》2009年第10期。)，因此本文选取的时间为2013～2017年。这样选取有一个好处：国内股票市场在2015年经历过一次急剧波动，该年份被包含在我们的样本时间跨度之内。我们希望研究在股票市场异常波动情况下期货市场的反应，并且2015年正好处于我们样本时间跨度的中间，可以较为完整地研究股票市场牛熊前后期货市场的价格走势。

(二) 基于MRS-SGED模型的识别结果

根据识别异常波动的MRS-SGED模型，利用极大似然参数估计方法，我们对中国各个商品期货市场以及金融期货市场30分钟时间序列进行了异常波动的识别。在模型拟合阶段，每个品种大概有7000～10000个样本，因为有些品种的上市日期较晚，比如铁矿石的上市日期为2013年10月18日，晚于我们选取样本时间跨度的起始日期。本文所用软件为Matlab2015b版本，并且借助于Marcelo Perlin(2015)(32)M. Perlin, “MS_Regress-the Matlab Package for Markov Regime Switching Models，” available at SSRN 1714016, 2015.发布的MRS程序包来估计模型参数。为了节省篇幅，每个期货交易所之代表性期货品种的收益率数据和通过模型识别出来的处于异常波动情形下的概率具体结果不在文中展示。(33)需要者请与本文作者联系。收益率的异常波动情形被MRS-SGED模型很好地识别了，并且异常波动呈现出稀疏性、非对称性和异常波动时期下的集聚效应。

(三) 平稳性检验和描述性统计

1. 平稳性检验

本文首先对上海期交所、郑州期交所和大连期交所交易最活跃的前五个期货品种流动性和收益率指标进行了平稳性检验，发现所有变量的ADF统计量在1%的置信水平上均是显著的(如表1所示)，因此都是平稳序列。

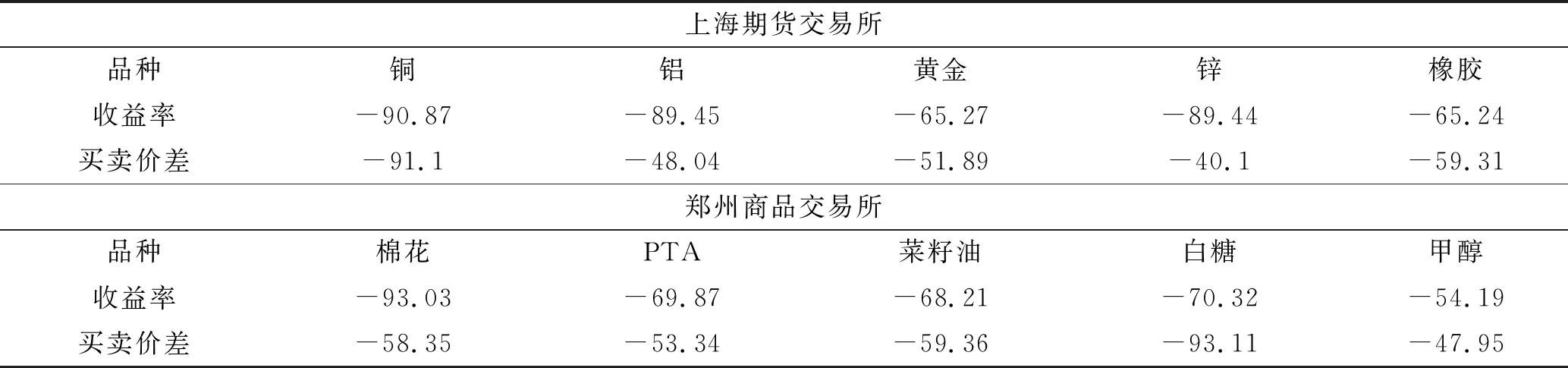
表1 流动性和收益率指标的ADF统计量

(续表)

2. 描述性统计

首先，表2给出了以30分钟为窗口期各期货收益率的均值和方差。可以看出，各个期货市场的平均收益水平均比较低；除了橡胶、甲醇、铁矿石和焦炭的波动性比较大之外，其他品种的波动性均相对较小。

表2还给出了作为流动性衡量指标的三大期货交易所主力期货品种买卖价差的基本统计量。数据显示，中位数均显著小于均值，这说明买卖价差受极值的影响非常严重，这可能和中国期货市场存在涨跌停板有关。当价格由于受到限制不能充分反映信息的时候，过多的挂单量就会单边集中于某一价格水平上，导致计算出来的买卖价差或市场深度也过大。此外，以PTA、橡胶等为代表的化工类期货买卖价差均值都普遍较高，这与其高交易成本直接相关。

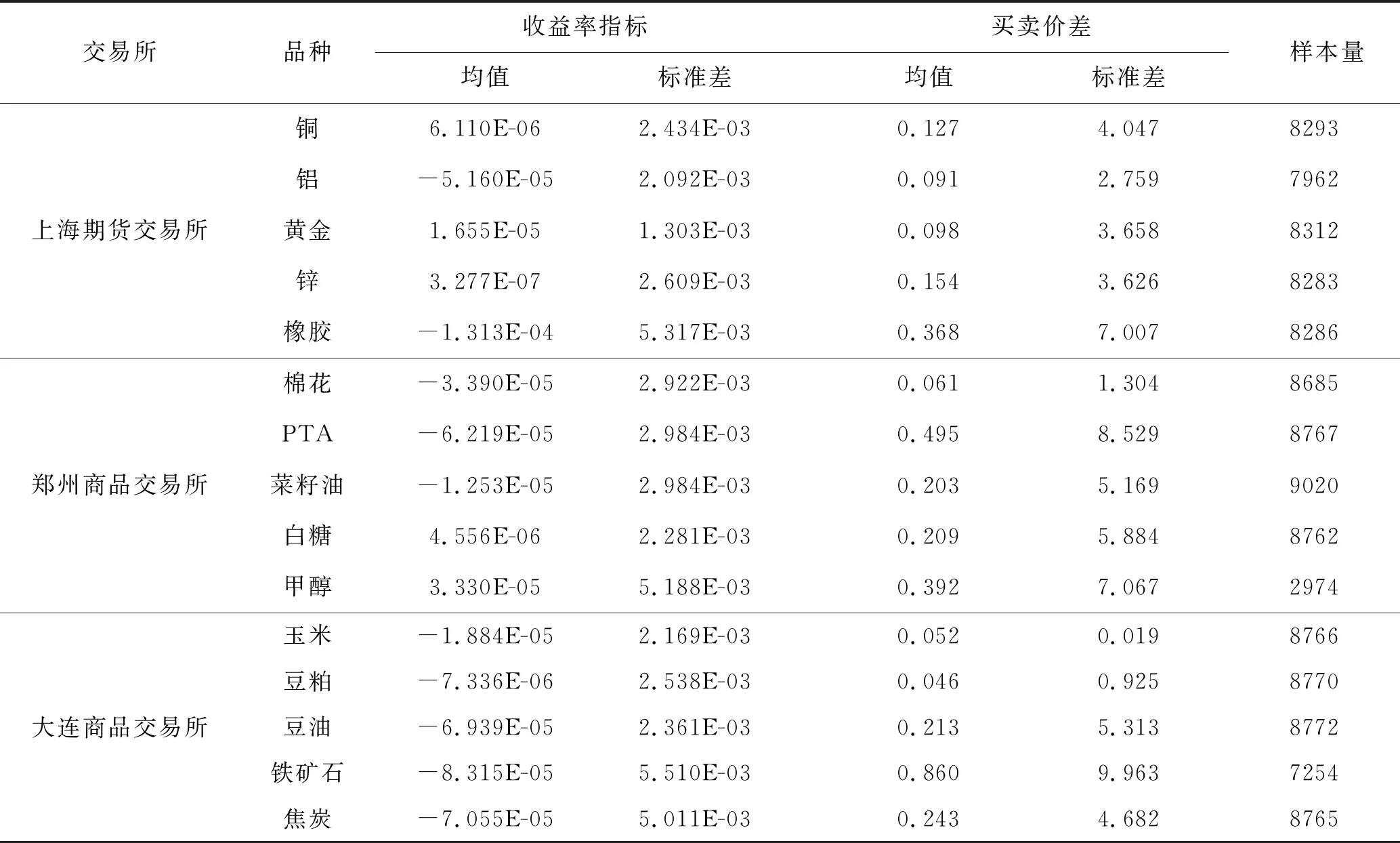
表2 收益率指标和期货品种买卖价差的基本统计量

表3分别给出了三大期货交易所各主力期货品种通过MRS-SGED模型识别出来的在不同波动状态下(正常或异常)市场深度的基本统计量。学者发现波动性与买卖价差呈现正相关性(Chung and Charoenwong, 1998)(34)K. H. Chung, & C. Charoenwong, “Insider Trading and the Bid-Ask Spread,” Financial Review 33.3 (1998): 1-20.，这表明流动性本身与波动性呈现负相关性。从标准差来看，除了白糖期货的买卖价差以外，其他期货品种买卖价差的标准差在异常波动时期均显著增大。总而言之，绝大部分期货品种的流动性指标在异常波动时期会减小，即流动性变差，但流动性指标的波动率上升，符合我们的预期。

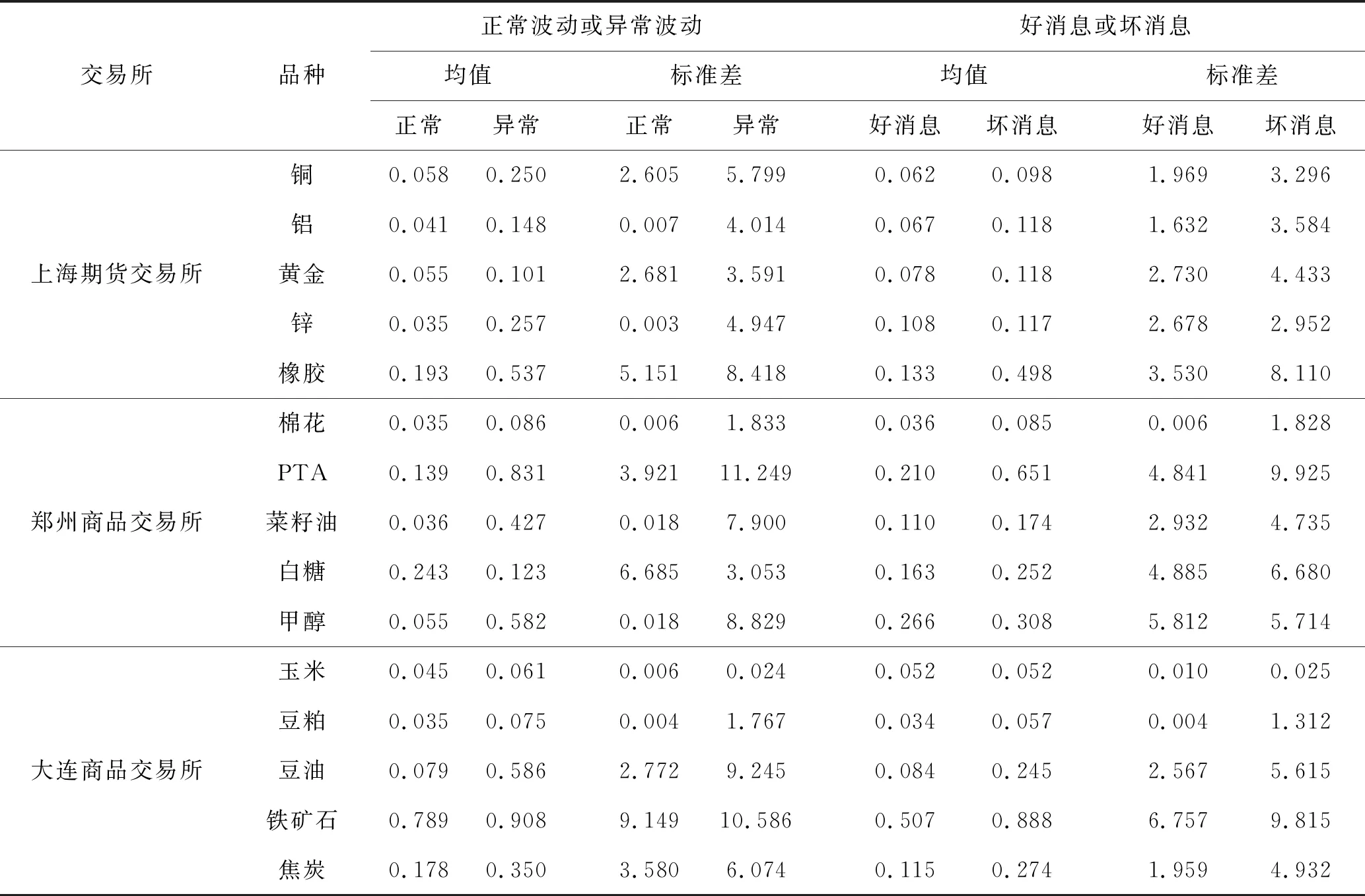
表3 期货品种买卖价差的基本统计量

表3还给出了三大期货交易所各主力期货品种在不同消息状态下(好消息或坏消息)买卖价差的基本统计量。从中位数指标来看，发现所有的期货品种的买卖价差在好消息和坏消息情况下差别不大，在数值上几乎一致；然而从均值指标来看，所有期货品种的买卖差价在坏消息时期都大于好消息时期，这体现了极值(尤其是坏消息时期)的存在。这说明消息的性质也许并不会对市场流动性的整体水平造成影响，但坏消息更容易引发市场的异常波动。从标准差指标来看，买卖价差的标准差在好坏消息变化下，绝大部分期货品种(仅除甲醇以外)在坏消息时期买卖价差的波动率是显著增大的，这与佟孟华等(2009)(35)佟孟华、刘丽巍、蔡玲玲：《流动性对股票价格波动影响的实证分析》，《当代经济研究》2009年第12期。、Cao and Wei(2010)(36)M. Cao, & J. Wei, “Option Market Liquidity: Commonality and Other Characteristics,” Journal of Financial Markets 13.1 (2010): 20-48.的观点相一致。他们都认为当市场处于下降行情时，投资者对未来预期的不确定性增加，因此市场流动性的波动性也会增加。从基本统计量分析可以发现，在不同消息状态下中国期货市场的流动性运作方式具有差异性，并且买卖价差在好消息和坏消息下的统计特征存在一定程度的非对称特征，不如区分异常波动和正常波动时的对称性强。

四、 异常波动下期货市场流动性溢价实证分析

根据前文流动性指标的选择，我们以买卖价差作为流动性溢价研究对象。被解释变量为以30分钟为间隔的收益率，解释变量为30分钟内的平均买卖价差。

(一) 不区分好坏消息的流动性溢价研究

根据公式(9)，本文进一步对三大期货交易所的主力期货品种合约进行分析，结果如表4所示。我们可以发现在两种波动状态下(正常或异常)仅有少部分主力期货品种的溢价参数在5%的显著性水平下显著，具体为豆油、菜籽油期货(异常波动)和PTA期货(正常波动)。结果表明，在两种不同的市场波动状态下，商品期货市场基于交易量信息的流动性溢价的存在性非常弱。总体来看，在能源期货、农产品期货与金属期货间并不呈现显著的流动性溢价差异。

表4 基于正常和异常波动的期货市场流动性溢价的实证结果

(二) 区分好坏消息的流动性溢价研究

根据公式(10)，本文对三大期货交易所的主力期货品种合约进行研究，结果如表5至表7所示。

(1) 在区分消息类型(好消息或坏消息)后，市场深度变得更为显著，大部分期货品种呈现出溢价关系，同时拟合度也大幅提高。尤其是上海期货交易所的期货品种，无论是在好消息还是坏消息期间，市场深度的参数在10%的置信水平下皆为显著的。这表明市场上存在着因不同消息类型而产生的流动性。

(2) 在异常波动条件下，所有期货品种的市场深度参数在1%的置信水平下都是显著的，同时基于不同消息类型的的流动性溢价具有显著的非对称性特征。除了玉米与甲醇外，其他期货品种的流动性溢价都具有正杠杆效应。在期货交易所中，上海期货交易所的期货品种流动性溢价全部具有正杠杆效应，即在好消息条件下，流动性溢价更为明显。在正常波动条件下，黄金、锌、菜籽油、玉米、豆粕和焦炭的流动性溢价具有反杠杆效应，铜、铝、橡胶、甲醇和铁矿石期货的流动性溢价都表现出正杠杆效应。所以异常波动下流动性溢价更能表现出一致的杠杆效应。

(3) 在异常波动状态下，没有区分消息类型前，仅有少部分的溢价关系显著；在区分消息类型后，大部分期货品种的溢价关系在任何一种消息条件下都变得显著。同时，系数在好消息或坏消息时分别为正、负，即市场流动性变大后，收益率绝对值将变大，这在双向收益的期货市场特征下是合理的。

(4) 对农产品、能源、金属三个期货种类进行分析。在正常波动情况下，金属产品中的铜和铝流动性溢价正杠杆效应最为显著，农副产品中的菜籽油和豆粕流动性溢价负杠杆效应最大。除了农产品中的白糖期货，其余种类期货在异常波动下均略大于1，各种金属产品期货一致符合正杠杆效应。尽管能源期货中的甲醇与农产品期货中的玉米在异常波动下略有背离，但这不影响本文的基本结论。

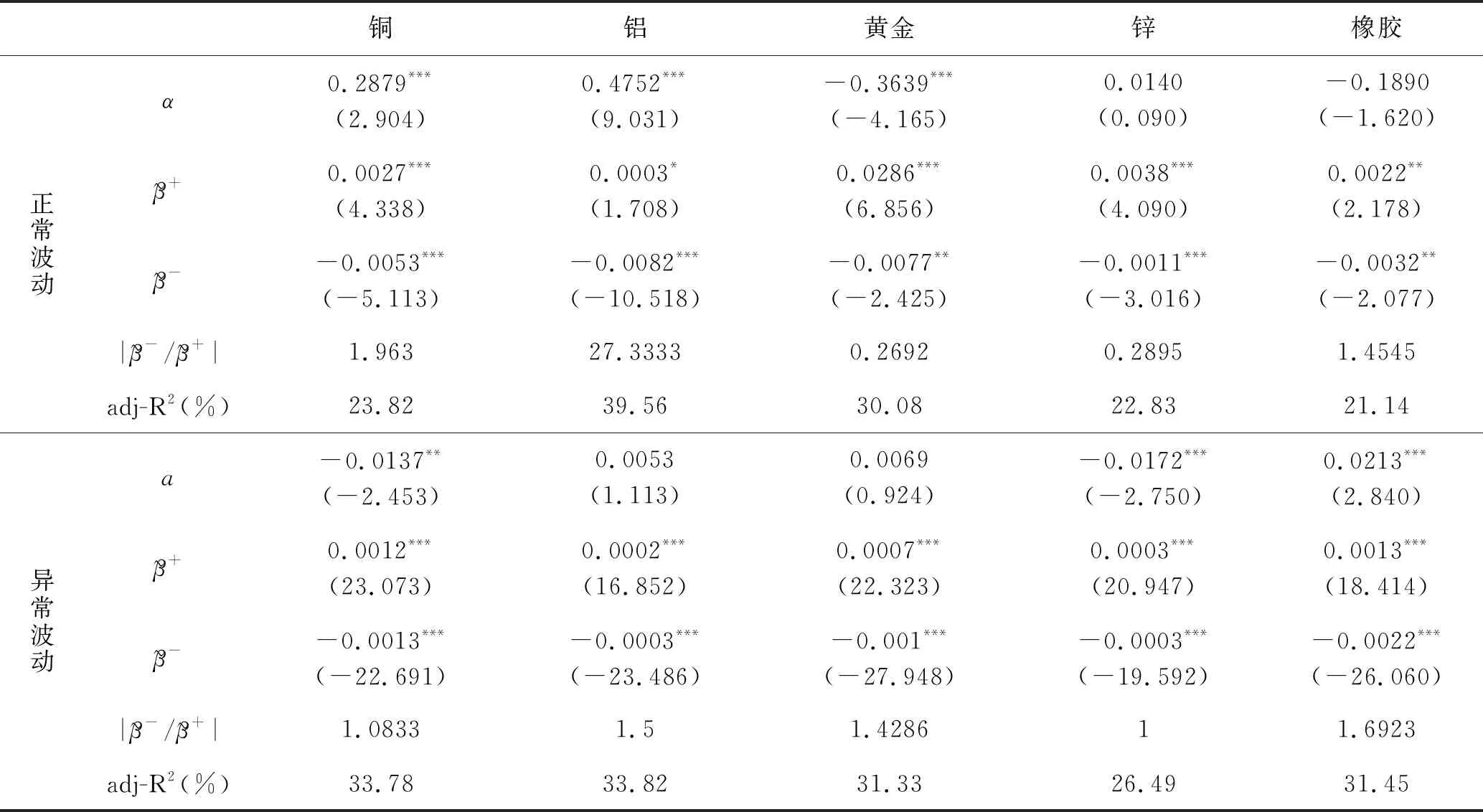
表5 上海期货交易所区分好坏消息下流动性溢价的实证结果

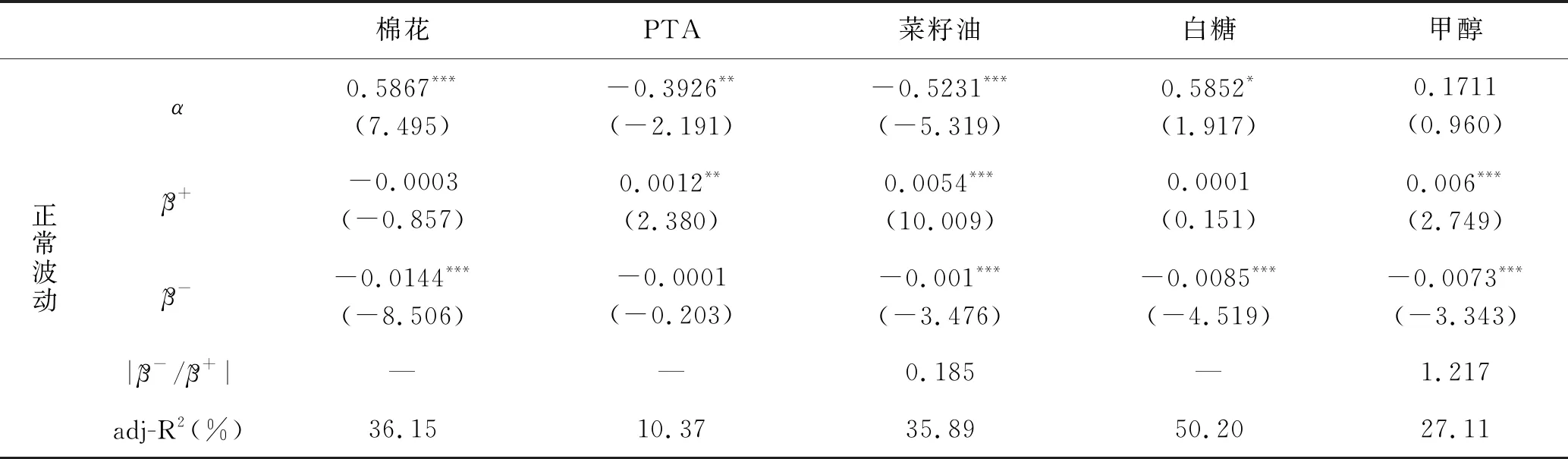
表6 郑州商品交易所区分好坏消息下流动性溢价的实证结果

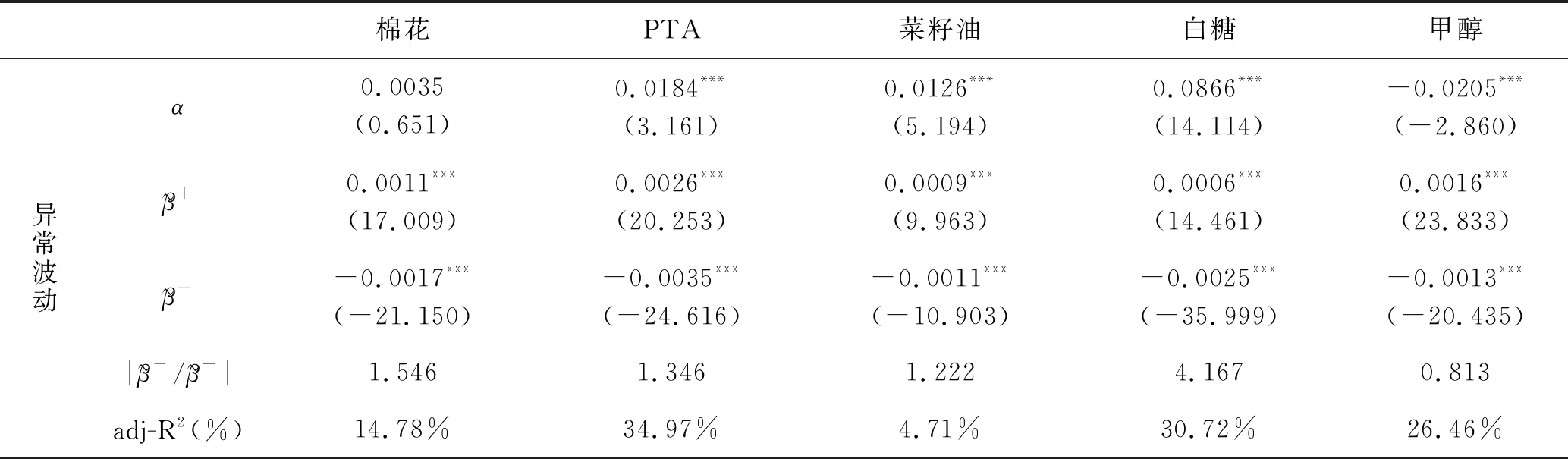
(续表)

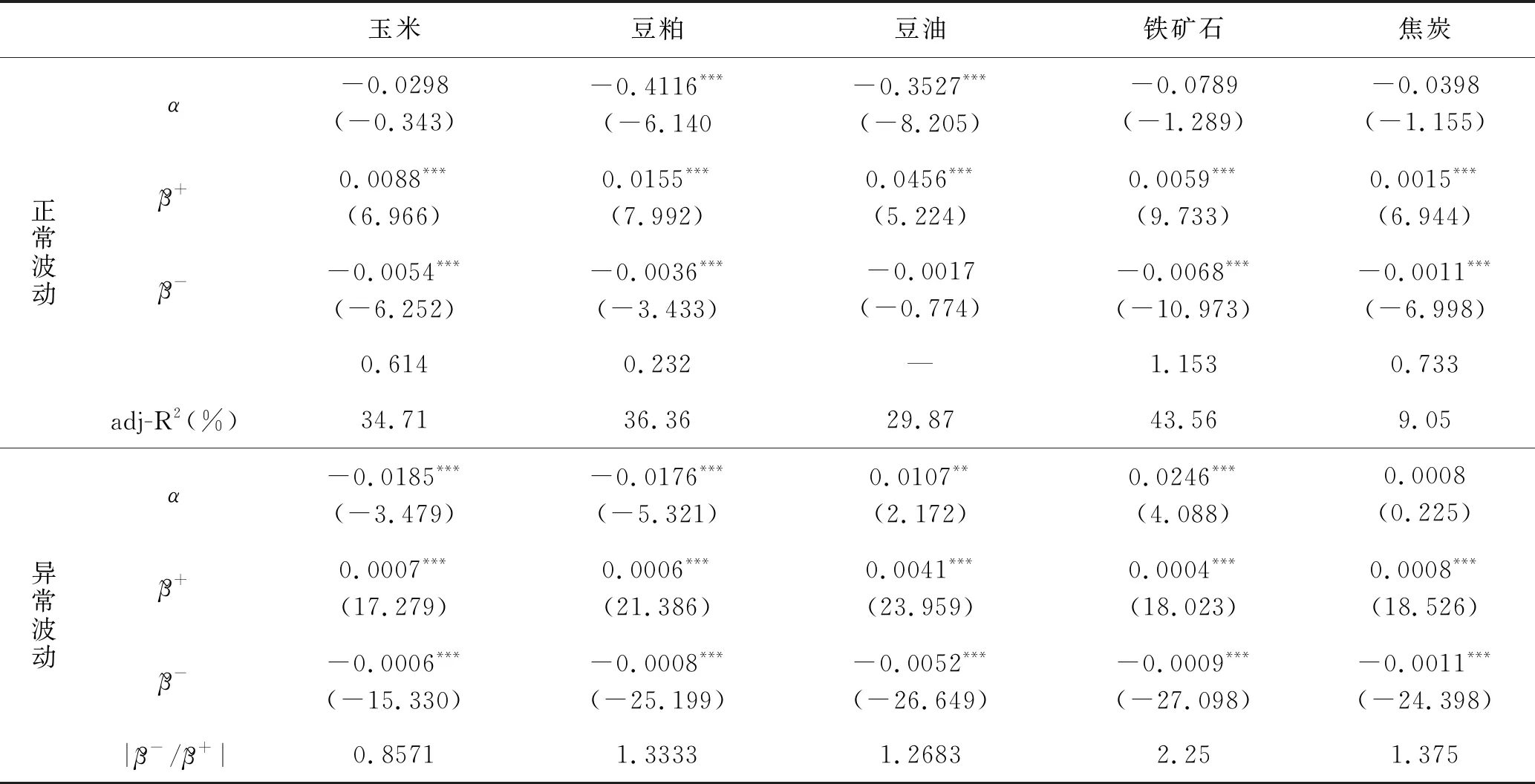
表7 大连商品交易所区分好坏消息下流动性溢价的实证结果

五、 结论与建议

异常波动状态下的期货市场流动性相较于正常状态具有丰富的信息内涵。为探索这一状态下中国期货市场的流动性溢价，本文首先利用MRS-SGED模型识别出了各时期期货市场所处的状态，在此基础上比较正常波动和异常波动下，以及好消息和坏消息下，流动性的基本统计特征。可以发现，异常波动呈现出稀疏性、非对称性和异常波动时期下的集聚效应。相对而言，绝大部分期货品种的流动性指标在异常波动时期会减小，即流动性变差。同时，商品期货市场的流动性在不同信息条件下的运作机制是不同的，买卖价差在好消息和坏消息下的统计特征存在一定程度的非对称特征。

在异常波动条件下，几乎所有品种均不存在流动性溢价；而在正常波动条件下，中国商品期货市场的流动性溢价的存在性也很弱。然而，与不区分好坏消息的异常波动情形相比，区分消息种类(好消息和坏消息)后买卖价差的显著性明显增强了；同时，大部分主力期货品种呈现出显著的流动性溢价关系，尤其是对于上海期货交易所的期货品种而言。由此说明，在中国期货市场存在基于好消息和坏消息的流动性溢价。此外，在异常波动条件下，基于好消息和坏消息的流动性溢价具有显著的非对称性特征。相对而言，在正常波动下，铜、铝、橡胶、甲醇和铁矿石期货的流动性溢价都表现出正杠杆效应，而黄金、锌、菜籽油、玉米、豆粕和焦炭期货的流动性溢价具有反杠杆效应。在异常波动下，流动性溢价能表现出一致的杠杆效应，其中金属产品期货完全符合该特征。

另外，我们对异常波动下流动性管理的策略进行了研究。这主要基于这样一个实证结果：异常波动下期货市场的流动性变差且波动率上升，而这种现象又会进一步导致市场波动性的增大乃至引发金融危机。鉴于此，对于投资者(主要是职业基金经理人)而言，在异常波动时期，应及早调整投资组合，配置较多的流动性好的资产，且更加注重高阶矩风险，将对于金融资产高阶矩的计算纳入投资组合的构建当中。

从我国监管机构及顶层设计的角度，本文的研究结果支持引入做市商制度的机制设计，应逐步放开涨跌停板限制以促进期货市场的流动性。同时，近年来，我国政府为引导资本市场高质量发展，不断加大我国金融市场的对外开放力度，资本账户适度开放。尤其在当下复杂的国际经济形势下，监管者应高度关注外国资本对我国期货市场流动性的冲击，加强事前监管，做好风险管控，避免金融市场的系统性风险，确保市场的正常运行。