Edge Coloring of Graphs with Applications in Coding Theory

Ghaffar Raeisi,Mohammad Gholami

Department of Mathematical Sciences,Shahrekord University,Shahrekord,P.O.Box 115,Iran

Abstract:In this paper,a new type of edge coloring of graphs together with an algorithm for such an edge coloring is presented to construct some columnweight three low-density parity-check (LDPC) codes whose Tanner graphs are free of 4-cycles.This kind of edge coloring is applied on some well-known classes of graphs such as complete graphs and complete bipartite graphs to generate some column-weight 3 LDPC codes having flexibility in terms of code length and rate.Interestingly,the constructed(3,k)-regular codes with regularities k=4,5,...,22 have lengths n=12,20,26,35,48,57,70,88,104,117,140,155,176,204,228,247,280,301,330,having minimum block length compared to the best known similar codes in the literature.In addition to linear complexity of generating such parity-check matrices,they can be considered as the base matrices of some quasi-cyclic(QC)LDPC codes with maximum achievable girth 18,which inherit the low-complexity encoder implementations of QC-LDPC codes.Simulation results show that the QC-LDPC codes with large girth lifted from the constructed base matrices have good performances and outperform random codes,progressive edge growth LDPC codes,some finite fields and group rings based QC-LDPC codes and also have a close competition to the standard IEEE 802.16e(WiMAX)code.

Keywords:low-density parity-check code;edge coloring;Quasi-cyclic LDPC code;girth;AWGN channel

I.INTRODUCTION

Low-density parity-check (LDPC) codes [1]are the most promising class of linear codes due to their ease of implementation and excellent performance over noisy channels when decoded with message-passing algorithms [2].LDPC codes are being considered in numerous applications including digital communication systems[3],MIMO-OFDM systems[4]and magnetic recording channels [5],because of the easy operation and simple decoding which improve the performance.Much research is devoted to characterizing the performance of LDPC codes and designing codes that have good performances.Based on the methods of construction,LDPC codes can be divided into two categories:random codes[6]and structured codes[7-22].Although randomly constructed LDPC codes of large length give excellent bit-error rate(BER)performance[6],the memory required to specify the nonzero elements of such a random matrix can be a major challenge for hardware implementation,while structured LDPC codes can lead to much simpler implementations,particularly for encoding.

To each parity-check matrixHof an LDPC code,theTanner graphTG(H) [23]is assigned which collects variable nodes and bit nodes associated to the rows and the columns ofH,respectively,and each edge connects a variable node to a bit node if the intersection of the corresponding row and column ofHhas a nonzero entry.We adopt the common notation of referring to a code with the parity-check matrix having column and row weightsjandk,respectively,as an(j,k)-regular LDPC code.The design rate of a(j,k)-regular LDPC code is given byR=1-j/k.

Thegirthof a code with the given parity-check matrixH,denoted byg(H),is defined as the length of the shortest cycle in TG(H)and is commonly considered to be one of the most important code parameter which determines the number of independent iterations [1].Cycles,especially short cycles,in TG(H) degrade the performance of LDPC decoders,because they affect the independence of the extrinsic information exchanged in the iterative decoding[6].It is known[23]that if the Tanner graph of the code is free of short cycles,then the iterative sum-product decoding algorithm converges to the optimal solution.In addition,a lower bound on the minimum distance of a code is given by Tanner [23]such that the lower bound increases with the girth of the code.Accordingly,the design of LDPC codes with large girth is of great interest and LDPC codes with large girth are preferred.

Different approaches have been studied to construct LDPC codes with large girth.Among the random-like approach constructions,the progressive edge growth(PEG) [24]is one of the most successful approaches for the construction of LDPC codes with large girth.PEG algorithm builds a Tanner graph by connecting the graphs nodes edge-by-edge provided that the added edge has minimal impact on the girth of the graph.Besides the PEG algorithm and its evolved construction algorithms,quasi-cyclic (QC) LDPC codes are the promising algebraic structured LDPC codes having applications in the storage systems[25],deepspace communications[26],broadband networks[27]and network coding [28].This is due to their lowcomplex encoding and efficient parallel iterative decoding,while the existence of short cycles,especially 4-cycles,is prohibited in their Tanner graph.Some algebraic structured constructions of QC-LDPC codes have been investigated in [7-22,29].Among the well known structured LDPC codes,finite geometry LDPC codes and LDPC codes constructed from combinatorial designs [13-21]are adequate for high-rate LDPC codes.The error correcting performance of these LDPC codes is verified under proper decoding algorithms but they have severe restrictions on flexibly choosing the code rate and length.Also,since finite geometry LDPC codes usually have much redundancy and large weights in their parity-check matrices,they are not suitable for a strictly power-constrained system with iterative message-passing decoding.

In this paper,the concept of the edge coloring of graphs is used to construct some well-structured block designs whose incidence matrices can be considered as the parity-check matrices of some regular and nonregular column-weight three LDPC codes.The family of parity-check matrices so obtained have Tanner graphs which are free of 4-cycles and the class of LDPC codes derived from our construction possesses flexibility in terms of code length and rate,which may have some possible applications to other typical wireless communications such as relaying[25]and MIMO systems[4].Interestingly,the constructed(3,k)-regular codes with regularitiesk=4,5,...,22

have lengthsn=12,20,26,35,48,57,70,88,104,117,140,155,176,204,228,247,280,301,330,having minimum block length compared to the best known similar codes in the literature.The constructed parity-check matrices can be considered as the base matrices of some QC-LDPC codes with girth at most 18.Simulation results show that the constructed QC-LDPC codes have good performances on AWGN channel and outperform than the random codes [6],PEG LDPC codes [24],codes constructed based on finite fields [8],[11],the group ring based QC-LDPC code constructed in[12],the(2300,1610)LDPC code constructed in[29].In addition,the constructed(2064,1290)QC-LDPC code with girth 8 has a close competition with the shortened (2064,1296)standard IEEE 802.16e(WiMAX)LDPC code[30].

The outline the paper is as follows.First,some graph theory preliminaries and definitions are given in Section II which will be used in the rest of the paper.In Section III,we give a new edge-coloring of graphs with an algorithm which will be used in Section IV to construct some column weight three LDPC codes with flexible rates and lengths.Then,in Section V,the proposed method is applied on several well-known classes of graphs such as complete,complete bipartite and disjoint union of complete graphs and the results will be summarized in Table1.In Section VI,some column-weight 3 QC-LDPC codes with girths at most 18 are constructed by lifting the base matrices proposed in Section V.Finally,in Section VII,some bit error rate(BER)performances of the constructed QCLDPC codes are provided and compared with some well-known LDPC codes.

II.PRELIMINARIES

To go through the details of the construction,we need some definitions from graph theory.LetG=(V,E)be a graph with vertex and edge setsVandE,respectively.Thedegreeof a vertexv ∈Vis the number of edges incident withvand a graph calledk-regularif all vertices have degreek.The maximum degree of vertices of a graphGis denoted by Δ(G),or simply by Δ.Two verticesuandvare adjacent if there is an edge betweenuandvand we write{u,v} ∈E(G).For a vertexv ∈V(G),we useN(v)to denote the set of all vertices ofGwhich are adjacent tov.Anindependent setin a graph is a set of pairwise nonadjacent vertices.We say that vertexvand edgeeareincidentifvis an endpoint ofe.Also,two edges ofGare incident if they have a vertex in common.A graph onnvertices in which any two vertices are adjacent is calledcomplete graphand denoted byKn.A graphGisbipartiteif the set of its vertices can be partitioned into two disjoint setsV1andV2such that no two vertices within eitherV1orV2are connected by an edge.A bipartite graphGwith partite setsV1andV2is denoted byG=(V1,V2).A bipartite graphG=(V1,V2)is calledcomplete bipartite graphif there is an edge between each vertex ofV1and each vertex ofV2.A complete bipartite graphG=(V1,V2)with|V1|=nand|V2|=mis denoted byKn,m.

Apathis a graph whose vertices can be ordered so that two vertices are adjacent if and only if they are consecutive in the list.Acycleis a graph with an equal number of vertices and edges whose vertices can be placed around a circle so that two vertices are adjacent if and only if they appear consecutively along the circle.Path and cycle onnvertices are denoted byPnandCn,respectively.The cycleCnis called even(odd)ifnis even(odd).

In graph theory,aproper k-edge coloringof ann-vertex graphGwith vertex setV(G)={1,2,...,n}is a labelingf:E(G)→C,where|C|=k(often we useC={n+1,n+2,...,n+k}

and we call it as thecolor set)and incident edges have different colors.The labels are called colors.By the Vizing's theorem [31],the minimum number of colors needed to color the edges of a simple graph is either its maximum degree Δ or Δ+1 and for bipartite graphs the number of colors is always Δ.However,distinguishing between graphs that require Δ colors and those that require Δ + 1 turns out be NP-hard,as was shown by Holyer [32].In [33]the author presents an algorithm for edge-coloring simple graphs using Δ+1 colors running intime,wheremis the number of edges andnis the number of vertices of graph.In [34],Greedy-Euler-Color algorithm is presented that uses Δ+1 colors and runs intime,imp√roving the result of[33]and removing a factor of afrom the runtime.Besides the edge-coloring algorithms,there are some explicit methods for edge-coloring of some spacial classes of graphs,given as follows.

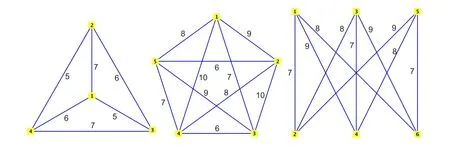
Figure1.An edge-coloring of K4,K5 and K3,3.

Complete graphs:Consider the complete graphKlwith vertex and edge setsV(Kl)={1,2,...,l}andE(Kl)={{i,j}:1≤i ＜j ≤l},respectively.Now,for oddl,color edge{i,j}byl+((i+j)(l+1)/2-1 (modl))+1,and for evenl,color edge{i,j},1≤i ＜j ＜lbyl+(i+j-1(modl-1))+1 and edge{i,l},1≤i ＜l,by colorl+(2i-1 (modl-1))+1.It is easy to see that this coloring yields a proper edge coloring ofKlwithlcolorsC={l+1,l+2,...,2l}whenlis odd,andl-1 colorsC={l+1,l+2,...,2l-1},whenlis even.Forl=4,5,proper edge colorings ofK4andK5are shown in Figure1.

Complete bipartite graphs:Consider the complete bipartite graphKl,lwith partite setsV1={1,3,...,2l-1}andV2={2,4,...,2l}.Coloring each edge{2i-1,2j},1≤i,j ≤l,by 2l+(2(j-i) (modl))+1 yields a proper edge coloring ofKl,lwithlcolorsC={2l+1,2l+2,...,3l}.For example,forl=3 such an edge coloring is given in Figure1.

Paths and Even Cycles:Consider the pathPl(resp.even cycleCl)with vertex setV={1,2,...,l}.Coloring edges ofPl(resp.Cl) alternatively by colorsl+1 andl+2 yields a proper edge coloring of pathPl(resp.Cl)with two colors.

III.NEW EDGE COLORING AND ALGORITHM

In this section,a new edge coloring of graphs with an algorithm is presented which will be used in the construction of some column weight three LDPC codes with flexible rates and lengths.LetGbe a given graph,V(G)={1,2,...,n},with a proper edge coloringf.Hereafter,for a vertexvofGwe useSvto denote the set of all colors appeared on the edges incident tov,i.e.Sv={f({v,w}):w ∈N(v)}.Note that inthe edge coloring of graphs presented in Section II,the set of colors is disjoint from the set of vertices of the graph.But in general,for an edge-colored graphGwith color setC,we may haveV(G)∩C /=∅,i.e.the set of colors can be selected from the labels of the vertices ofG.In this case,we consider an additional propertyPon the edge coloring.We say that the proper edge coloringfof a graphGsatisfiesproperty Pif for everyu,v ∈V(G),

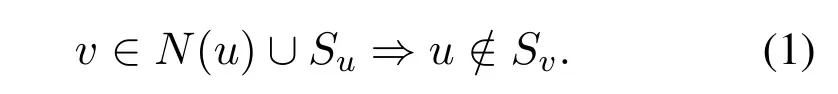
In fact,property(1)says that ifvis a neighbor ofuor a color appeared on the edges incident withu,thenucan not be considered as a color on edges incident with vertexv.For instance,in Figure2,two edgecolored graphs are presented so that some of colors are selected from the set of vertices and these colorings satisfying propertyP.In Figure2,part (a),the set of vertices ofGisV(G)={1,...,8}and the set of colors isC={1,3,5,7,9,10}.In this figure,N(1)∪S1={2,4,7,8,9,10},and so the color 1 can not be appeared on the edges incident with vertices 2,4,7,8.

Hereafter,we suppose that all edge colorings are proper and satisfying propertyP.Note that ifV(G)∩C=∅,then any proper edge coloring ofGwith color setCsatisfies propertyP.Thus,we consider propertyPfor all edge colorings in which the color set intersect the vertices ofG.In the sequel,an algorithm is presented which greedily provides a proper edge coloring of a simple graph satisfying propertyP.In fact,for a given specific permutationσon the edges of the graph,Algorithm 1 assigns to each edge the smallest available color satisfying propertyPand using a new color(a color disjoint from the vertex set) if needed.Note that,to find the smallest possible number of colors,we need to consider all possible permutations on the edges of a graph.But considering all possible permutations on the edges of a graph requires a high complexity,we can apply a randomized method to select some permutations such that the number of colors used by the algorithm is small as possible.This algorithm returns the setBconsisting triples{a,b,c}such that{a,b}is an edge of the graph andcis the color assigned to this edge.Since the complexity of finding the smallest element of a set isO(1),then the complexity of Algorithm 1 isO(m+n)in whichnandmare the number of vertices and edges of the graph,respectively.As in a simple graph we haven ≤2m,then the complexity of the algorithm isO(m),which is linear in terms of the number of the edges of graph.

?

In the sequel,we give an example of a graph whose edges are colored by Algorithm 1.

Example III.1.Let G be the 20-vertex Flower Snark graph,depicted in Figure2 part(b),with the edge set E={{1,2},{1,5},{1,6},{2,3},{2,9},{3,4},{3,12},{4,5},{4,15},{5,18},{6,7},{6,20},{7,8},{7,17},{8,9},{8,13},{9,10},{10,11},{10,20},{11,12},{11,16},{12,13},{13,14},{14,15},{14,19},{15,16},{16,17},{17,18},{18,19},{19,20}}.Applying Algorithm 1 on G,we obtain the following set of triples containing edgeswith their colors.

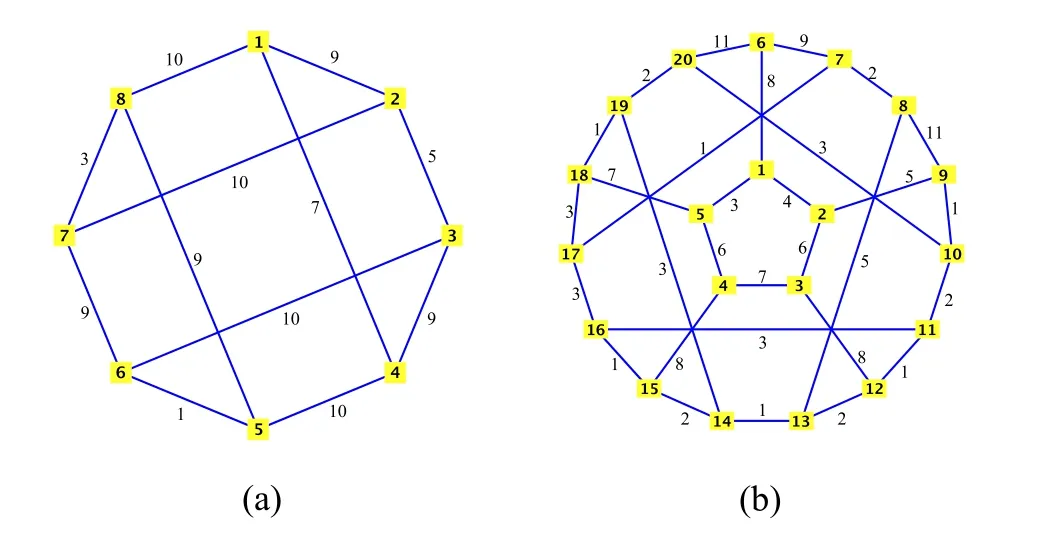
Figure2.An edge-coloring of the (a) cube graph and (b)Flower-Snark graph,satisfying property P.

Note that,the color set in an edge coloring of a graph derived from Algorithm 1 may have some intersections with the vertex set of the graph.In the following,a necessary and sufficient condition is given such that the output of Algorithm 1 is disjoint from the vertex set of the graph.

Theorem III.2.Let G be an arbitrary graph whose edges are colored by Algorithm 1 with color set C.Then V(G)∩C=∅if and only if for every edge e=uv,N(u)∪N(v)=V(G).

Proof.First,letV(G)∩C=∅and on the contrary,lete=uvbe an edge such thatN(u)∪N(v)/=V(G).Consider a vertexw ∈V(G)N(u)∪N(v).Clearly Algorithm 1 can choosewas the color of the edgee,contradicts the fact thatV(G)∩C=∅.

Now,let for every edgee=uv,N(u)∪N(v)=V(G)and letCbe the set of colors used by Algorithm 1.LetV(G)∩C /=∅and on the contrary,letw ∈V(G)∩Cis used as the color of an edgee=uv.AsN(u)∪N(v)=V(G),without loss of generality,we may assume thatw ∈N(u).Thusu ∈N(w)andw ∈Su,contradicting the propertyPin Eq.1,completing the proof.

IV.CODE CONSTRUCTION

In this section,the method of the code construction is presented which is based on the edge coloring presented in Section III.To go through the details of the construction,we need some concepts from the combinatorial mathematics.For positive integersvandb,a (v,b)-designis a set ofpoints V={1,2,...,v}together with a family of sizebof subsets ofVcalledblocks,whose members are chosen to satisfy in some set of properties that are deemed useful for a particular application.Theincidence matrixof a (v,b)-design is av×bbinary matrix(hi,j),in which the rows and the columns are corresponding to the points and the blocks,respectively,such thathi,j=1 if thei-th point belongs to thej-th block andhi,j=0,otherwise.In this paper we are interested in the construction of designs whose incidence matrices are free of 4-cycles i.e.any two points are contained in at most one block.

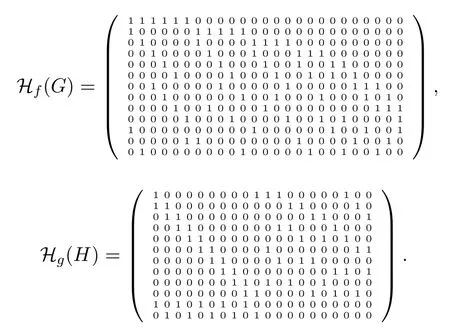
LetGbe ann-vertex graph withmedges and letfbe a proper edge coloring ofGon the set of colorsCsatisfying propertyPand|C V(G)|=t.LetBf(G) denote the set of all triples{a,b,f({a,b})},wheree={a,b}is an edge ofGwith colorf({a,b}).Iffis known,we simply writeB(G) instead ofBf(G).ClearlyBf(G) is a (n+t,m)-design.IfHf(G) denotes the (n+t)× mincident matrix ofBf(G),thenHf(G) is the parity-check matrix of a column-weight 3 LDPC code with lengthmand rateFor example,iff,gare the edge colorings ofK4andK3,3,respectively,shown in Figure1,thenBf(K4)={{1,2,7},{3,4,7},{1,3,5},{2,4,5},{1,4,6},{2,3,6}}andBg(K3,3)={{1,2,7},{3,4,7},{5,6,7},{2,3,8},{4,5,8},{1,6,8},{1,4,9},{3,6,9},{2,5,9}},with the following incidence matrices:

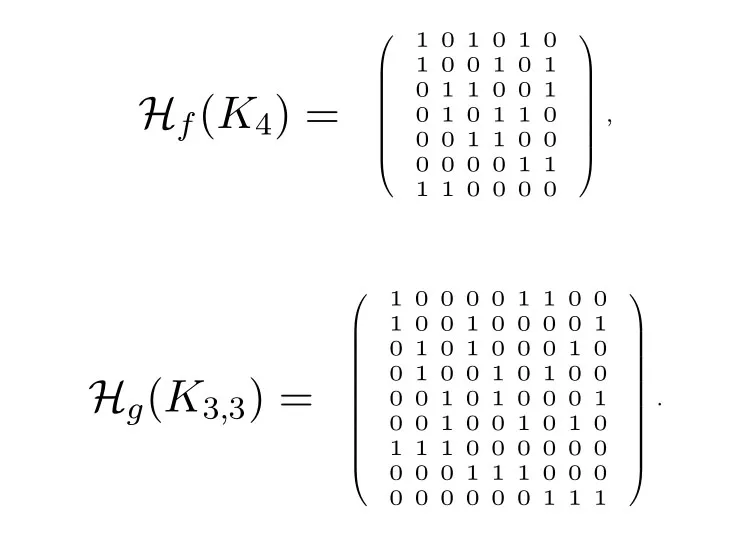
Example IV.1.Consider graphs G and H shown inFigure3,parts(a)and(b)with the presented edge colorings f and g,respectively.Clearly,

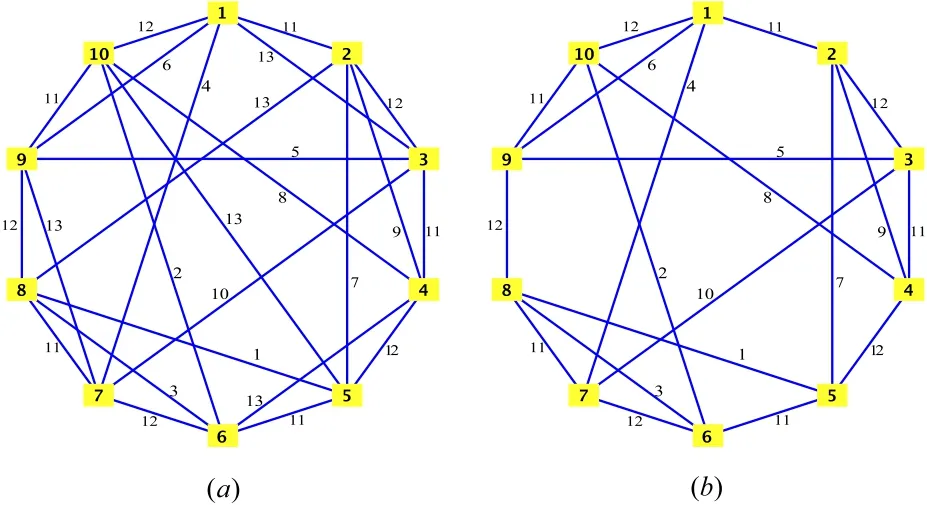
and

with the following13×25and12×20incidence matrices,respectively.Note that Hg(H)corresponds to the parity-check matrix of a(3,5)-regular code of length 20.

Now,Consider graphsG1,G2,...,Glwith edge coloringsf1,f2,...,fl,receptively,such that for each,V(Gi)∩V(Gj)=∅.IfG=(G1,G2,...,Gl)and Γ=(f1,f2,...,fl),then we defineBΓ(G)=If Γ is known,we simply denoteBΓ(G)byB(G).IfHΓ(G) denotes the incident matrix ofBΓ(G),thenHΓ(G) is the parity-check matrix of a column-weight 3 LDPC code,denoted byCΓ(G).In the following,we prove thatCΓ(G)is free of 4-cycles.

Lemma IV.2.Let G=(G1,G2,...,Gl)be a class of disjoint graphs with the proper edge coloringsΓ=(f1,f2,...,fl),respectively.Then CΓ(G)is free of 4-cycles.

Proof.Since all graphsG1,G2,...,Glare disjoint,i.e.V(Gi)∩V(Gj)=∅,CΓ(G) is free of 4-cycles if and only if everyHfi(Gi),1≤i ≤l,is free of 4-cycles.Therefore,it is sufficient to prove that for each graphGwith the edge coloringf,Hf(G),is free of 4-cycles.The existence of a 4-cycle inHf(G) is equivalent to the existence of two distinct blocksBi={ai,bi,f({ai,bi})}andBj={aj,bj,f({aj,bj})}such that|Bi ∩Bj|=2,where{ai,bi},{aj,bj} ∈E(G)andf({ai,bi})is the color of the edge{ai,bi}.SinceGis a simple graph andfis a proper edge coloring ofG,we may consider the following cases:

Case 1.ai=ajandf({ai,bi})=f({aj,bj}).

In this case,we have incident edges{ai,bi}and{ai,bj}having the same color inG.This contradicts the fact thatfis a proper edge coloring ofG.

Case 2.ai=ajandf({ai,bi})=bj.

In this case,{ai,bi}is colored bybjand sobj ∈Sai.In addition,ai=ajand{ai,bi} ∈E(G)implies thatai ∈N(bj).Therefore,we obtain thatbj ∈Saiandai ∈N(bj),which contradicts propertyPin Eq.1.This contradiction shows thatCΓ(G)is free of 4-cycles.

The following proposition shows that an arbitrary set can be considered as the points of a design of the formBf(G),for some graphGand edge coloringfofG.

Proposition IV.3.If V is an arbitrary set,then there exist some graph G and edge coloring f of G so that Bf(G)is a design on V.

Proof.Let|V|=nand considerG=Pn−2with the proper 2-edge coloringf,described in Section II.Label the vertices and colors inGby elements ofV.ClearlyBf(G)define a design onVcontaining some 3-sets ofV.

Note that for a given positive integern,the design used in the proof of Proposition IV.3 just containsn-2 blocks.But,in general we are looking for some graphsGwith an edge coloringfsuch thatBf(G) contains the maximum possible number of blocks onnpoints.

Now,letGbe ann-vertex graph and letfbe an edge coloring ofGwith color setC′.SetC=C′ V(G).Also,let vertices ofGbe partitioned into disjoint independent setsV1,V2,...,Vlsuch that|Vi| ≥3.By Proposition IV.3,we may considerl+1 graphsG1,G2,...,Gl,Gcwith edge coloringsf1,f2,...,fl,fc,respectively,such thatBfi(Gi),1≤i ≤l,is a design on the setViandBfc(Gc) is a design on the setC.SetG=(G1,G2,...,Gl,Gc)and Γ=(f1,f2,...,fl,fc) and letB(Gf,GΓ)=Bf(G)∪BΓ(G).ClearlyB(Gf,GΓ)is a design on the setV(G)∪Cand ifG=∅,thenB(Gf,GΓ)=Bf(G).Hereafter,inB(Gf,GΓ) we callGas the base graph and (G,Γ) as the generator set.If edge coloringsfand Γ are known,then we simply denoteB(Gf,GΓ)byB(G,G).It is easy to see that the incidence matrixH(Gf,GΓ)ofB(Gf,GΓ)can be considered as the parity-check matrix of a column-weight three LDPC code with girth 6 having the following matrix form.

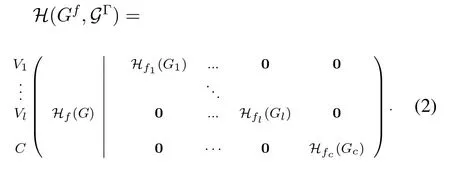
Note:It is worth noticing that in the complete graphG=Kl,we just consider the incidence matrix of the design on the set of colors i.e.Hfc(Gc).Thus,ifG=Gcthen

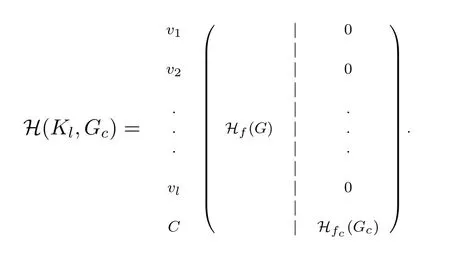
For edge colored bipartite graphG=(V1,V2),|V1|,|V2| ≥3,with color setC,we just consider the designs on the partite setsV1,V2and the sets of colorsC.Thus,ifG=(G1,G2,Gc)then

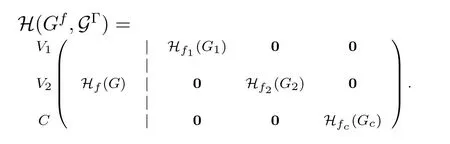
Example IV.4.1.Let G=K4be the complete graph with V(K4)={1,2,3,4}and consider the edge coloring of K4with color set C={5,6,7},shown in Figure1.Let Gc=K2with vertex set{5,6} colored by 7.If G=(∅,∅,∅,∅,K2),then B(Gc)={5,6,7} and so B(K4,G)={{1,2,7},{1,3,5},{1,4,6},{2,3,6},{2,4,5},{3,4,7},{5,6,7}}with the following incidence matrix H(K4,G).

2.Consider G=K3,3with partite sets V1={1,3,5},V2={2,4,6}and edge-color set C={7,8,9}.Consider G1=K2with vertex set{1,3} colored by 5,G2=K2with vertex set{2,4} colored by 6 and G3=K2with vertex set{7,8}colored by 9.Thus B(G1)={1,3,5},B(G2)={2,4,6} and B(Gc)={7,8,9}.If G=(K2,K2,K2),then B(K3,3,G)={{1,2,7},{3,4,7},{5,6,7},{2,3,8},{4,5,8},{1,6,8},{1,4,9},{3,6,9},{2,5,9},{1,3,5},{2,4,6},{7,8,9}}with the following incidence matrix H(K3,3,G).

3.Consider G=C6with vertex set {1,2,...,6}ordered in clockwise order.Consider partite sets V1={1,3,5},V2={2,4,6} and let f be a proper edge coloring of G with color set C={7,8}.Set G1=K2with vertex set {1,3} colored by 5,G2=K2with vertex set {2,4} colored by 6 and Gc=∅.If G=(K2,K2,∅),then B(C6,G)={{1,2,7},{2,3,8},{3,4,7},{4,5,8},{5,6,7},{6,1,8},{1,3,5},{2,4,6}}with the following incidence matrix H(C6,G).

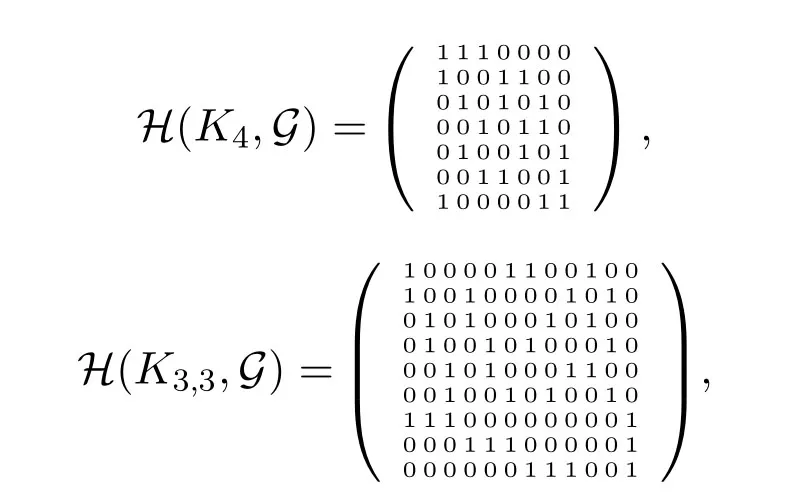
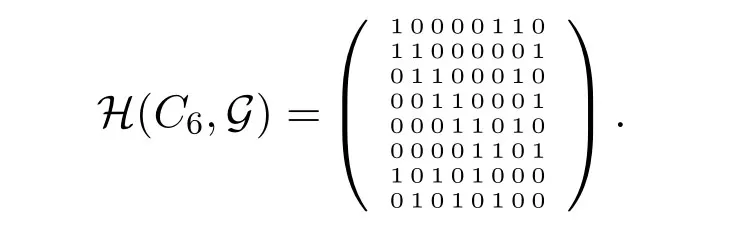
Example IV.5.Let G be the10-vertex graph on vertices {1,2,...,10},shown in Figure3,with the presented edge coloring f having color set C′={1,2,...,13}.Set C=C′ V(G)={11,12,13}and let Gc=K2with vertex set {11,12} colored by 13.If G=(∅,...,∅,K2),then B(Gc)={11,12,13}and so B(G,G)={{1,2,11},{2,3,12},{3,4,11},{4,5,12},{5,6,11},{6,7,12},{7,8,11},{8,9,12},{9,10,11},{1,10,12},{1,3,13},{1,9,6},{1,7,4},{2,4,9},{2,5,7},{2,8,13},{3,7,10},{3,9,5},{4,6,13},{4,10,8},{5,8,1},{5,10,13},{6,10,2},{7,9,13},{6,8,3},{11,12,13}}.The incidence matrix of this design can be considered as the parity-check matrix of a(3,6)-regular code with length 26.

To generate LDPC codes with higher rates,the construction of the parity-check matrix presented in Eq.2 can be extended as follows.LetGbe ann-vertex graph with edge coloringfhaving color setC′.SetC=C′ V(G).Also,let vertices ofGbe partitioned into disjoint independent setsV1,V2,...,Vlsuch that|Vi|=ni ≥3.For disjoint graphsG1,G2,...,Gl,Gcwith edge coloringsf1,f2,...,fl,fc,receptively,and generator sets(G1,Γ1),...,(Gl,Γl),(Gc,Γc),let{1,2,...,l,c}be constructed such that1≤i ≤l,is a design onViandis a design onC.Let Hibe the incidence matrix ofBi=1≤i ≤l,and Hcbe the incidence matrix ofSet B=(B1,...,Bl,Bc)and define:

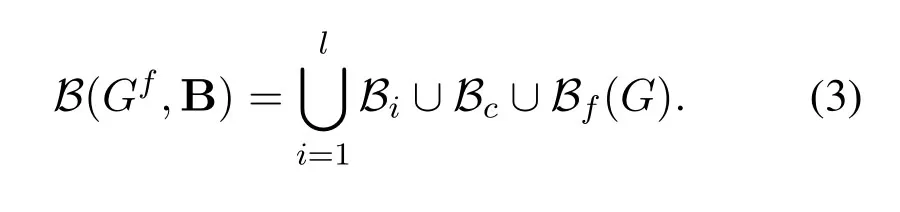
The incidence matrix of the constructed design in(3),can be considered as the following form.Since this matrix is based onGand H=(H1,...,Hl,Hc),thus we denote this matrix byH(Gf,H).

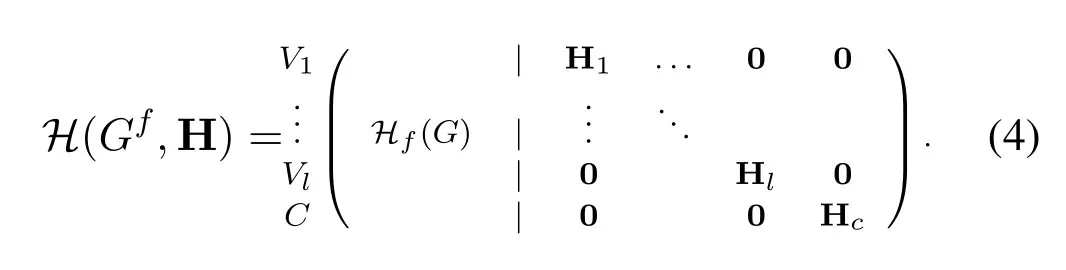
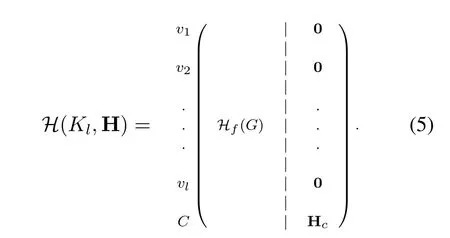
Note:It is worth noticing that for edge colored complete graphG=Kl,we just consider H=Hcand so

For edge colored bipartite graphG=(V1,V2),we consider H=(H1,H2,Hc)and so

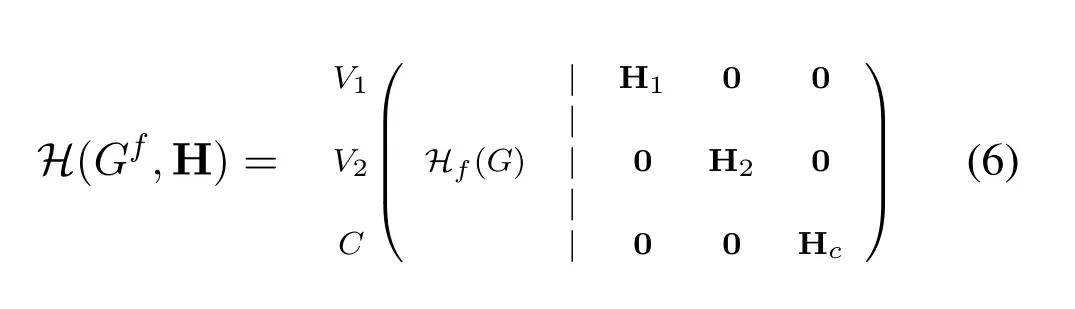
In the following theorem,we show thatH(Gf,H)is free of 4-cycles and soH(Gf,H) can be considered as the parity-check matrix of a column-weight three LDPC code with girth at least six,denoted byC(Gf,H).

Theorem IV.6.For every graph G with the given edge coloring f,C(Gf,H)is free of 4-cycles.

Proof.Consider the parity check matrix ofC(Gf,H),presented in(4).Sincefis a proper edge coloring ofG,we conclude thatHf(G)is free of 4-cycles and by Lemma IV.2,each Hiis free of 4-cycles.Also,by the definition ofC(Gf,H),the existence of a 4-cycle containing a column of Hiand a column ofHf(G)is avoidable becauseViis an independent set inG.This means thatC(Gf,H) is free of 4-cycles,completing the proof.

V.CODES BASED ON THE EDGE COLORING OF SOME SPACIAL GRAPHS

In this section,we apply the proposed method on several well-known classes of graphs such as complete,complete bipartite and disjoint union of complete graphs and the parameters of the corresponding codes will be summarized in Table1.

5.1 Complete Graphs

Consider the complete graphKlwith the proper edge coloringfdescribed in Section II with color setC.As the construction ofHf(Kl) is clear,then by Eq.5,it is sufficient to determine Hc.Note that,the existence of Hcis guaranteed by Proposition IV.3,for eachl ≥2,but to construct codes with higher rates,different graphs can be used to construct Hc.For example,forl ∈{7,8,9,10,13,15,19},in the following some matrices Hcare constructed such that the corresponding codes are regular,having the minimum block length and the best rates compared to the known similar codes in the literature.In the sequel,we suppose thatV(Kl)={1,2,...,l}and we consider the edge coloring ofKlintroduced in Section II with color setC.

1.Forl=7,8,let Hc=H(K4,G)be the incidence matrix of the design constructed in Example IV.4,part 1 on the pointsC={l+1,l+2,...,l+7}.Note that the constructed matrices can be considered as the parity-check matrices of a (3,6) and a (3,7)-regular LDPC code with girth 6 having lengths 28 and 35,respectively.

2.Forl=9,10,let Hc=H(K3,3,G) be the incidence matrix of the design constructed in Example IV.4 part 2,on the pointsC={l+1,l+ 2,...,l+ 9}.The constructed matrices can be considered as the parity-check matrices of a (3,8)-regular and a (3,9)-regular LDPC code with girth 6 having lengths 48 and 57,respectively.

3.Forl=13,let Hcbe the incidence matrix of the design constructed in Example IV.5 on the pointsC={14,...,26}.ClearlyH(K13,Hc) can be considered as the parity-check matrix of a(3,12)-regular LDPC code with girth 6 and length 104.

4.Forl=15,16,let Hcbe the incidence matrix of the design constructed in part 1 based onK8on the pointsC={16,17,...,30}.Therefore,H(K15,Hc)andH(K16,Hc)are the paritycheck matrices of a girth-6 regular column-weight three LDPC code with regularities 14,15,respectively.

5.Forl=19,let Hcbe the incidence matrix of the design constructed in part 2 based onK10with color setC={20,...,28}.Therefore,H(K19,Hc) can be considered as the paritycheck of a regular column-weight three LDPC code with regularity 18 and girth 6.

5.2 Complete Bipartite Graphs

In this section,we examine the constructed codes based on the edge coloring of complete bipartite graphKl,land by Eq.6,it is sufficient to consider H1,H2,Hc,whereCis the set of colors in an edge coloring ofKl,l.Here,we suppose thatKl,l=(V1,V2),whereV1={1,3,...2l -1},V2={2,4,...,2l}and we consider the edge coloring ofKl,lintroduced in Section II with color setC={2l+1,2l+2,...,3l}.

1.Forl=6,let H1=H2=Hcbe the incidence matrix of the designBf(K2,2),wherefis the edge coloring introduced in Section II.Thus if H=(H1,H2,Hc),thenH(K6,6,H) can be considered as the parity-check matrix of a(3,8)-regular LDPC code with girth 6 and length 48.

2.Forl=7,let H1=H2=Hcbe the incidence matrix of the design constructed in Example IV.4,part 1.Thus if H=(H1,H2,Hc),thenH(K7,7,H)can be considered as the paritycheck matrix of a(3,10)-regular LDPC code with girth 6 and length 70.Moreover,using the constructed matrixH(K7,7,H) as the matrix HcinH(K21,Hc) andH(K22,Hc) presented in (5),one can construct a(3,20)-regular and a(3,21)-regular LDPC code with girth 6 having lengths 280 and 301,respectively.

3.Forl=8,let H1=H2=Hcbe the incidence matrix of the design constructed in Example IV.4,part 3,and set H=(H1,H2,Hc).Therefore,H(K8,8,H) is the incidence matrix of a regular column-weight three LDPC code with regularity 10,girth 6 and length 88.

4.Forl=9,let H1=H2=Hcbe the incidence matrix of the design constructed in Example IV.4,part 2,and H=(H1,H2,Hc).Therefore,H(K9,9,H) is the parity-check matrix of a 4-cycle free regular column-weight three LDPC code with regularity 13 and length 117.

5.Forl=12,let H1=H2=Hcbe the incidence matrix ofBg(H) constructed in Example IV.1 and set H=(H1,H2,Hc).Therefore,H(K12,12,H) is the parity-check matrix of a girth-6 regular column-weight three LDPC code with regularity 17 and length 204.

5.3 Disjoint Complete Graphs

For oddl,letNlbe the graph with vertex setV(Nl)={1,2,...,3l}containing three disjoint copies of complete graphswith vertex sets{l+1,l+2,...,2l}and2,...,3l}.Using the edge coloring ofKlpresented in Section II,any edge coloring of a copyas the color setas the color setK(2)land finally useas the color setFor this purpose,it is sufficient to color each edge{i,j}inby coloreach edge{i,j}inby color 2l(modl))+1 and finally each edge{i,j}inby colorAlso,one can easily see that the set of verticesVi={i,l+i,2l+i},1≤i ≤l,form an independent set inNland so the vertices ofNlcan be partitioned into independent sets of size 3.Now,for eachi,1≤i ≤l,considerGi=K2with vertex set{i,l+i}which is colored by 2l+i.IfG=(G1,G2,...,Gl),thenH(Gl,G)is the parity-check matrix of a 4-cycle free regular LDPC code with regularity (3l -1)/2,as shown in Theorem V.2.If the rows ofH(Nl,G)are indexed by the vertices in the setsV1,V2,...,Vl,thenH(Nl,G)has the following matrix form in which,1 and 0 are 3×1 full one and full zero matrices,respectively.SinceG=(G1,G2,...,Gl) is known,soH(Nl,G)just depends onNland thus,we use(Nl)instead ofH(Nl,G).

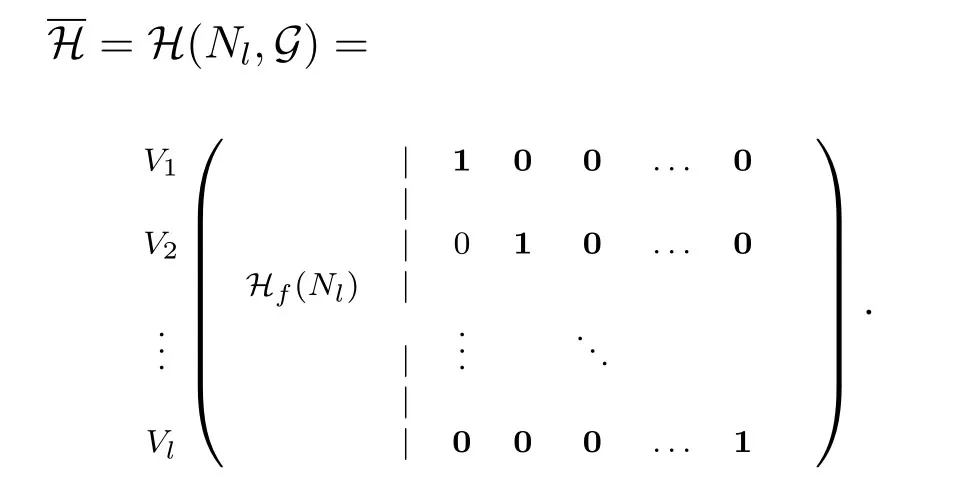
Example V.1.If l=3,then V(N3)={1,2,...,9}and sets V1={1,4,7},V2={3,6,9} and V3={2,5,8}are independent sets in N3.The corresponding design based on N3is {{1,2,6},{1,3,5},{2,3,4},{4,5,9},{4,6,8},{5,6,7},{3,7,8},{2,7,9},{1,8,9},{1,4,7},{2,5,8},{3,6,9}}with thefollowing parity-check matrix

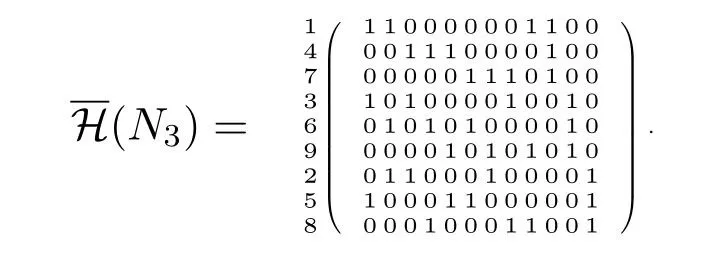
The following theorem confirms that the codes constructed based on disjoint union of complete graphs are 4-cycle free regular codes.

Theorem V.2.For any odd l,the incidence matrix can be considered as the parity-check matrixof a 4-cycle free regular LDPC code with regularity(3l-1)/2.

Proof.By Lemma IV.2,Hf(Nl) is free of 4-cycles.Thus it is sufficient to prove that for eachi,1≤i ≤l,the submatrix of(Nl) induced by the rows labeled withViis free of 4-cycles.To see this,we prove that for eachk,k=0,1,2,the set of colors appeared on the edges incident with vertex labeled byi+kl(Si+kl)does not include the colori+k′l,wherek′=k+ 1(mod3).Without loss of generality,we prove the assertion fork=0.Indeed,leti+l ∈Si.This means that for some vertexj,1≤j ≤l,we haveor equivalently,(i+j)(l+1)=2i(modl),which resultsi=jand this is imposable.This observation shows thatis free of 4-cycles.Now,each vertex in a copy ofKlhas degreel-1 and this vertex is used(l-1)/2 times as a color of an edge in the second copy ofKlinNl.Therefore,by the structure of(Nl),the constructed code is regular with regularity(3l-1)/2.

To see the flexibility in regularity,Table1 summarize the parameters of the constructed (3,k)-regular LDPC codes for differentk,4≤k ≤22,as described in this section.The constructed(3,k)-regular codes with regularitiesk=4,5,...,22 have lengthsn=12,20,26,35,48,57,70,88,104,117,140,155,176,204,228,247,280,301,330,having minimum block length compared to the best known similar codes in the literature.1,2,3,needslcolors for oddl.Use

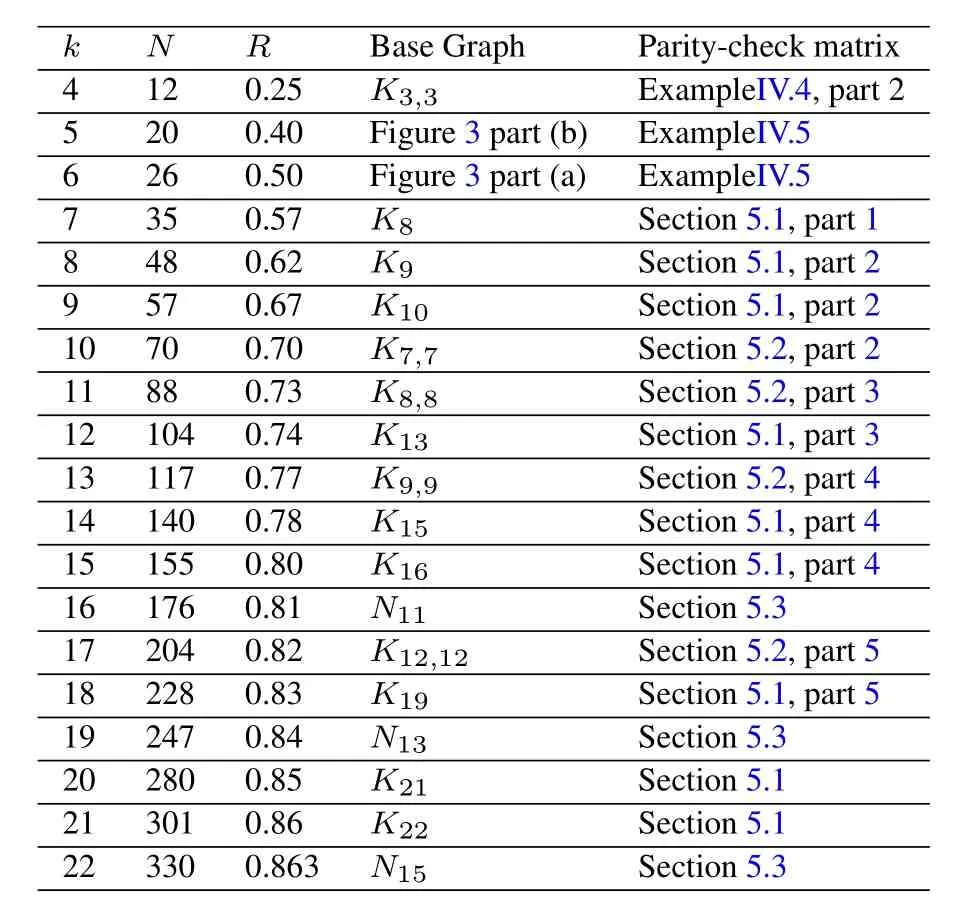
Table1.(3,k)-regular codes with regularity k,length N an rate R

VI.QC-LDPC CODES WITH GIRTHS AT MOST 18

Although LDPC codes have good error performances over AWGN channel,their encoding complexity was a drawback for their implementation until the recent two decades and the invention of the quasi-cyclic LDPC(QC-LDPC) codes.QC-LDPC codes have advantages over other types of LDPC codes in hardware implementation of encoding [18]and decoding [9,15].These features have made the design of QC-LDPC codes an attractive research area and lots of methods,including algebraic methods,are proposed for constructing QC-LDPC codes.The parity-check matrix of the constructed column-weight 3 LDPC codes in this paper are free of 4-cycles and so they can be considered as the mother matrix of some column-weight three QC-LDPC code with maximum achievable girth 18[7].In the sequel,we give an algorithm to generate such QC-LDPC codes with girths at most 18.

LetNandsbe nonnegative integers with 0≤s ≤N -1.By anN ×N circulant permutation matrix(CPM)shifted by s,IsN,we mean the matrix obtained fromN ×Nidentity matrixINby shifting each rowspositions to the bottom,that isI0N=INand for 1≤s ≤N -1,For simplicity,IsNwill be denoted byIs,whenNis known.

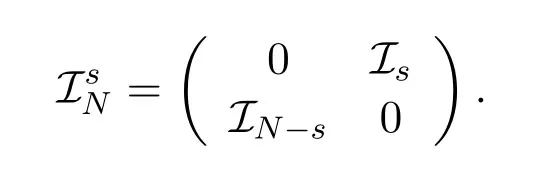
For a given integerNand the base matrixHwithcnonzero elements,we define a (c,N)-slope vectoras a vectorSof lengthcsuch that each component ofSbelongs to ZN={0,1,···,N -1}.Now,letNbe a positive integer andH=(hi,j)p×qbe the binary base matrix withcnonzero elementshi1,j1=hi2,j2=...=hic,jc=1.For a given(c,N)-slope vectorS=(s1,s2,...,sc),letHN,H,Sbe thepN × qNmatrix obtained from the base matrixHby replacing the zero elements with the zeroN×Nmatrix and the non-zero elementhik,jkbyIsk.

LetHbe ap×qbinary base matrix withcnonzero elements andG=TG(H) be the corresponding Tanner graph with the edge setE={e1,...,ec}.For sufficiently large positive integersNandg,3≤g ≤9,we give a deterministic algorithm generating a (c,N)-slope vectorS=(s1,...,sc) inductively (eachsicorresponds to the edgeei) such that the girth of TG(HN,H,S) is at least 2g.SetA1={0,1,...,N -1}and chooses1∈ A1arbitrarily.Now,letA1,...,Ak−1be chosen and(s1,...,sk−1)∈A1×···× Ak−1.At stepk,we chooseAkcontaining all elementssk ∈{0,...,N -1}such thatg(s1,...,sk)≥2g,whereg(s1,...,sk)is the minimum of 2l,such that for some 2l-length closed walkW=ei1ei2...ei2l,ei2l+1=ei1,k ∈{i1,i2,...,i2l} ⊆{1,...,k},ij /=ij+1,1≤j ≤2l,we have(modN).

?

The process to generate slope vectors is summarized in Algorithm 2.In fact,for a column-weight three LDPC code with base matrixH=(hi,j)v×b,a(c,N)-slope vectorS=(s1,...,sc),c=3b,can be generated from Algorithm 2 column-by-column starting from the first column traversing each column from top to bottom.For this purpose,let in thej-th column ofH,hi1,j=hi2,j=hi3,j=1,i1＜i2＜i3,be the non-zero elements of this column with the corresponding slopessji1,sji2andsji3,respectively.Without loss of generality,we may suppose thatsji1=0,otherwise we can subtractsji1fromsji2andsji2to obtain new slopes 0,sji2- sji1,andsji3- sji1.Therefore,hereaf ter,we may suppose thatsi=0,fori ≡1 (mod 3) and so a (c,N)-slope vectorS=(s1,. ..,sc),c=3b,can be denoted by a length 2b-vectorS=(s2,s3, s5,s6,...,sc−1,sc).

Applying Algorithm 2 on the constructed base matrices generated in Example III.1,Example IV.4 part 2,Example IV.5 and Section 5.1 part 1,Table2 provides some slope vectorsScorresponding to some QC-LDPC codes with girth at most 18.

VII.SIMULATION RESULTS

Using software available online [35],we have obtained simulation results on additive white Gaussian noise (AWGN) channel with BPSK modulation and the decoding algorithm is the sum-product algorithm.This section provides some BER comparisons between the error performance of the constructed QCLDPC codes on the one hand and random-like counterparts[6],PEG LDPC codes[24],codes constructed based on finite fields[8],[11],a group ring based QCLDPC code constructed in [12],the code constructed in[29]and a shortened IEEE 802.16e(WiMAX)code[30],on the other hand.

In the figures,byRand(p×q)we mean the 4-cycle free Mackay random code of lengthqand dimensionpand byPEG(q,tgb) we mean the lengthqcode generated by the progressive edge growth(PEG)algorithm having target girthb.In addition,C(N,G,gb)is used to denote the constructed girth-bQC-LDPC code based on graphGhaving CPM-sizeN.

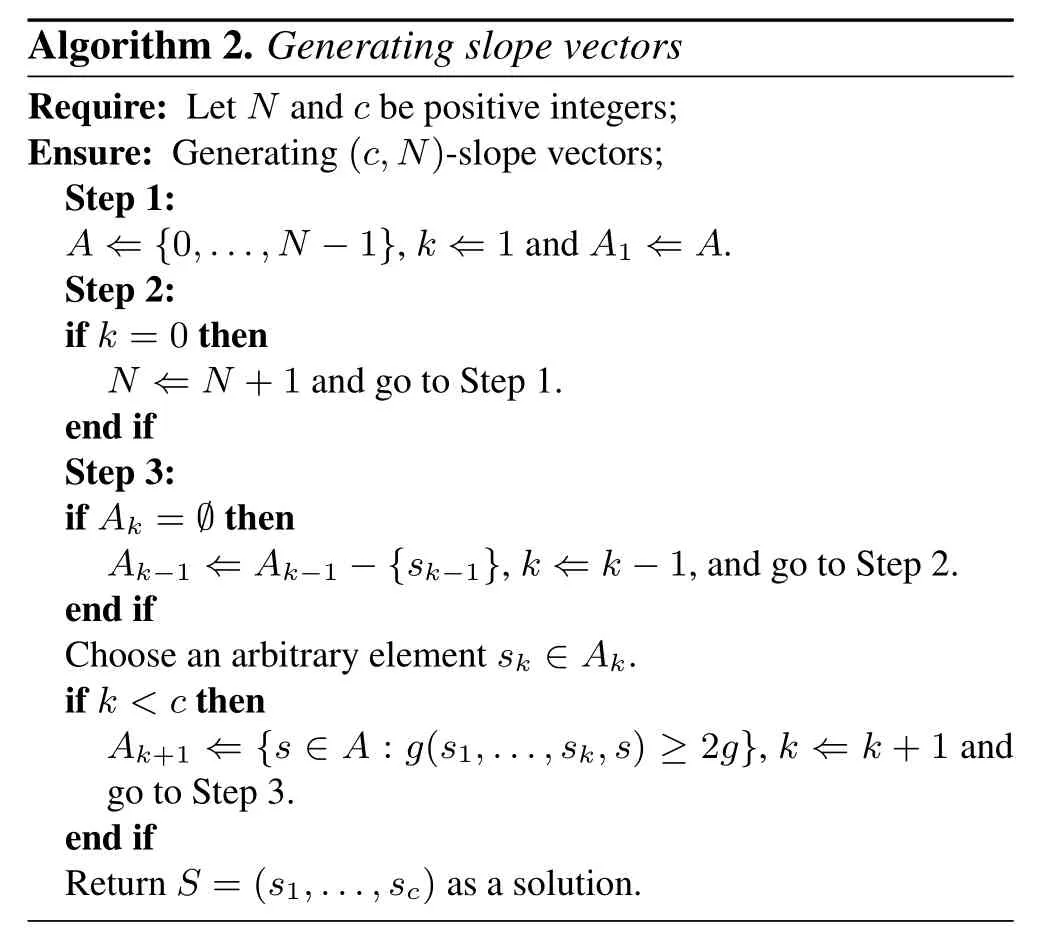
Applying Algorithm 2 on the base matrices constructed in Example IV.4 part 2,and Section 5.1 part 1,some QC-LDPC codes with same lengths and rates but different girths are constructed and the BER performance comparisons of these codes(with 20 iterations)are presented in Figure4.The figure confirms the superiority of the constructed codes with large girth and also confirms that the girth has a direct impact on the codes performance.As shown in Figure4,the constructed codes with large girths have good performances over AWGN channel.

In Figure5,the parity-check matrix of the code in Section 5.1 part 2 (based onK9) is used as the base matrix of a girth-8 QC-LDPC code generated by Algorithm 2.The performance of this code (with 30 iterations) is shown in Figure5.At the BER of 10−6,the code performs 1.8 dB from the Shannon limit and it outperforms the random codeRand(774×2064),the PEG codePEG(2064;tg8)and the(2040,1279)-LDPC code constructed in[12]based onZ8(a group of order 8).Moreover,the constructed code has a close competition to the(2064,1296)-LDPC code obtained by shortening of the standard(2304,1536)IEEE 802.16e(WiMAX)code[30].

Consider the girth-8(3,10)-regular QC-LDPC code of length 2030 lifted from the base matrix constructed in Section 5.2 part 2.The BER performance of this code is presented in Figure6 with 30 iterations.Included in this figure,the 4-cycle free(2032,1439)-LDPC code constructed in[8](Example 1) based on finite fields and the (2300,1610)-LDPC code constructed in [29].As the figure shows,there is a close competition between the constructed code and the random codeRand(609×2030),the PEG codePEG(2030;tg8)and outperform the codes constructed in[8]and[29].

Figure7 provides a comparison between the girth-8 QC-LDPC code with the base matrix constructed in Section 5.3 based on the graphN11,on the one hand and the random codeRand(726×3872),the PEG codePEG(3872;tg8) and the 4-cycle free(3969,3243)-LDPC code with minimum distance at least 63 constructed in [11](Example 3) based on finite fields,on the other hand.The performance of this code(with 50 iterations)is shown in Figure7.In this figure,all compared codes have length 3872 and rate 0.817 and at the BER of 10−6,our code performs 1.3 dB from the Shannon limit,while the (3969,3243)-LDPC code constructed in [11]has 1.6 dB far away the Shannon limit.Moreover,we see that the constructed code slightly outperforms its corresponding random code.

Table2.Slope vectors S associated to some QC-LDPC codes with rate R and CPM-size N.

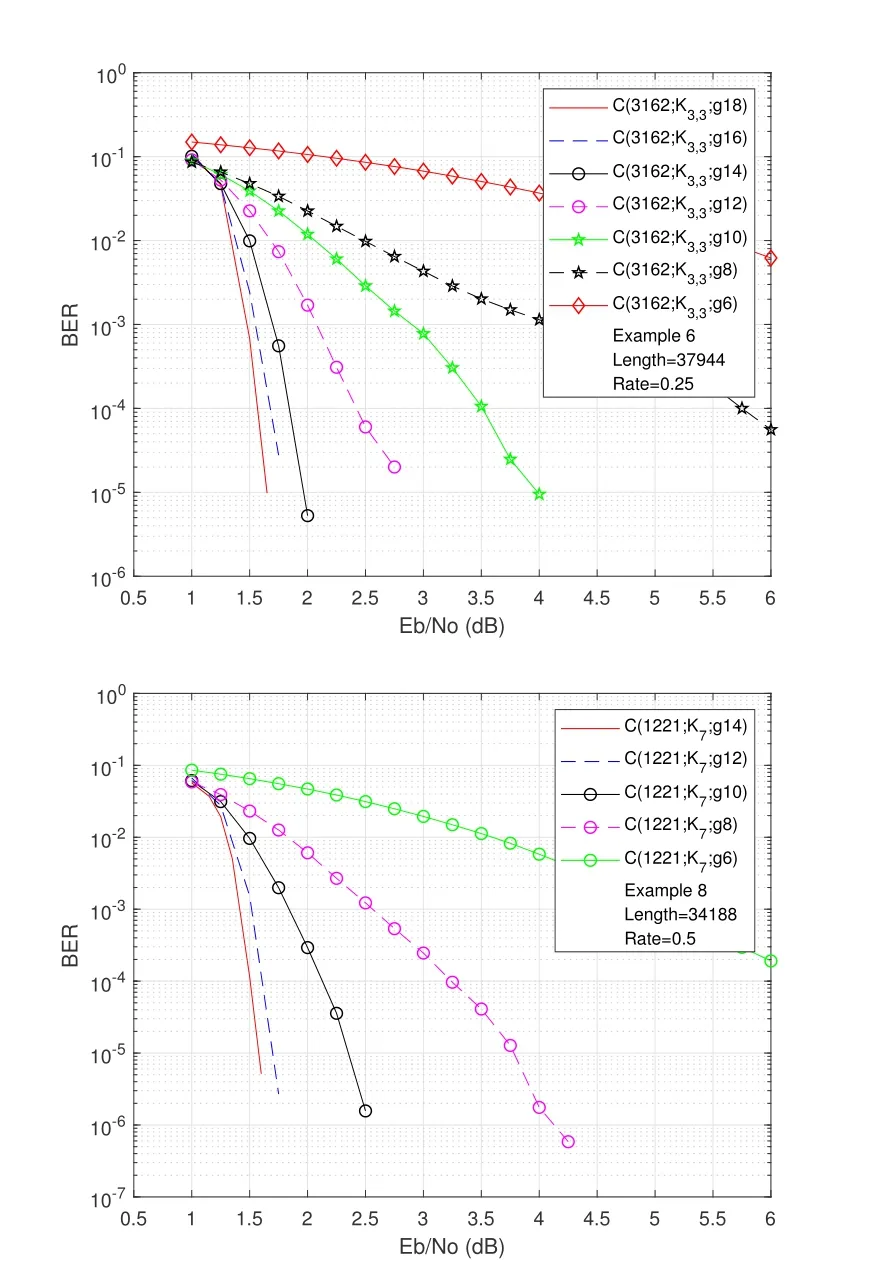
Figure4.The BER performance comparisons between the QC-LDPC codes with different girths having base matrices constructed in Example IV.4,part 2,and Section 5.1,part 1.

CONCLUSION

In this paper,a new class of column-weight three LDPC codes are presented whose Tanner graphs are free of 4-cycles.This construction is based on a new kind of edge coloring of graphs and the codes raised have flexibility in terms of code length and rate.Interestingly,the constructed (3,k)-regular codes with regularities 4≤k ≤22 have minimum block length compared to the known similar codes in the literature.The QC-LDPC codes lifted from the constructed base matrices have maximum achievable girth 18 and as simulation results show,they have good performances and perform better than the random codes,PEG LDPC codes,some algebraic and group ring based QC-LDPC codes and also have a close competition to the standard IEEE 802.16e(WiMAX)code.

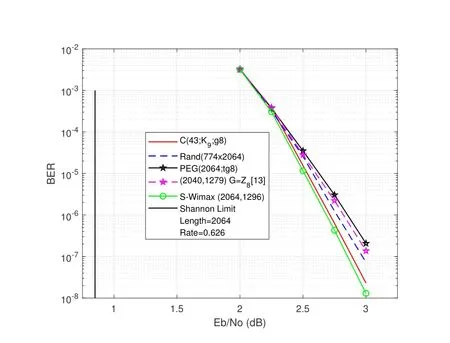
Figure5.A QC-LDPC code lifted from the base matrix in Section 5.1,pare 2,against random,PEG,the(2040,1279)-LDPC code in [12]and the shortened IEEE 802.16e(WiMAX)(2064,1296)-LDPC code.

Figure6.A QC-LDPC lifted from the base matrix in Section 5.2,part 2,against random,PEG,the 4-cycle free(2032,1439)-LDPC code in[8]and the(2300,1610)-LDPC code constructed in[29].

ACKNOWLEDGMENT

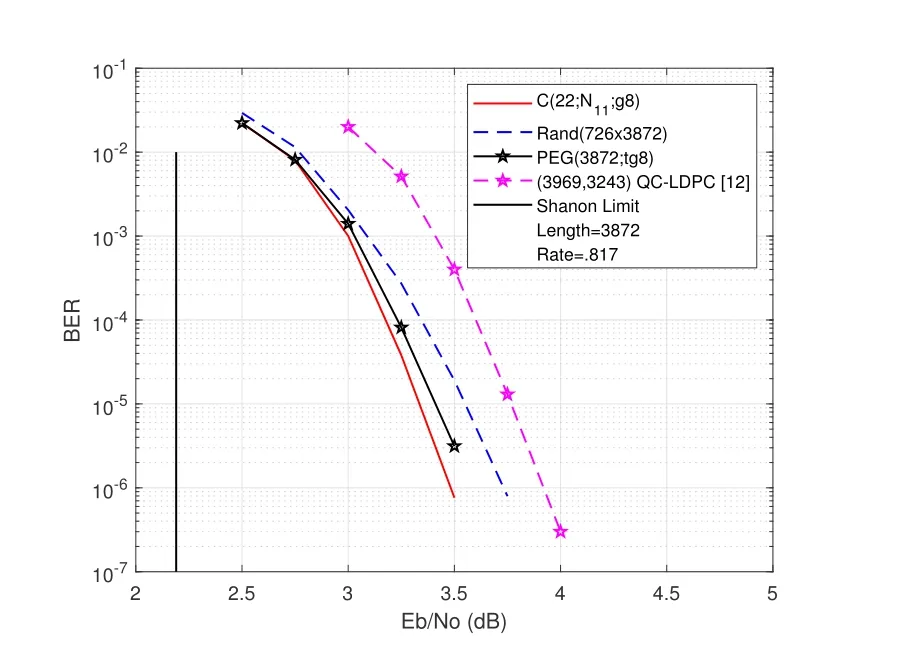
Figure7.A QC-LDPC code lifted from the base matrix(N11)against random,PEG and the(3969,3243)-LDPC code in[11].

The authors would like to thank anonymous referees for their valuable comments enabled us to greatly improve the quality of the paper.The research of the first author is partially supported by Shahrekord University grant No.97GRN1M1465.