Power Allocation for NOMA in D2D Relay Communications

Yan Cai,Chunhua Ke,Yiyang Ni,Jun Zhang,Hongbo Zhu

1 Jiangsu Key Laboratory of Wireless Communications,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

2 Jiangsu Second Normal University,Nanjing 210013,China

Abstract:Non-orthogonal multiple access(NOMA)is considered as one of the key technologies for the fifth generation (5G) wireless communications.The integration of NOMA and device-to-device (D2D)communications has recently attracted wide attention.In this paper,a relaying D2D communications assisted with cooperative relaying systems using NOMA(DRC-NOMA) is considered.We analyze the ergodic sum-rate for the proposed system and then derive the closed-form expressions.In addition,an optimal power allocation strategy maximizing the ergodic sum-rate is proposed based on these analysis results.Numerical results show the good agreement between the results of analysis and Monte Carlo method.The proposed DRC-NOMA has a great improvement of the ergodic sum-rate in the small regime of average channel gain of D2D pair.

Keywords:device-to-device communication;nonorthogonal multiple access;decode-and-forward relaying;power allocation;rate analysis.

I.INTRODUCTION

With the tremendous growing number of smart sensors and mobile devices,the demand for the mobile traffic will increase exponentially [1].In order to accommodate the emerging data demands,D2D communications underlaying cellular networks has attracted much attention due to the potential of offloading traffic load of base stations(BSs),saving power consumption of user equipment,increasing network spectrum efficiency and extending cellular coverage [2,3].Apart from D2D communications,NOMA is considered as a novel technique to improve the spectral efficiency and provide massive connectivity which has received a great interest[4].Comparing with the conventional orthogonal multiple access (OMA) technique,multiple users are allowed to reuse resource with different power level and successive interference cancellation(SIC)is adopted in decoding in NOMA[5,6].

Recently,the combination of NOMA technology and D2D communications was investigated to enhance the spectral efficiency,as well as,the number of connections of NOMA systems[7-11].The authors in[7]and[8]proposed a novel NOMA-based D2D communications framework,where the concept of D2D group was presented for the scenario that one D2D transmitter communicate with multiple D2D receivers simultaneously using the NOMA technique.The authors in[9]proposed a full-duplex D2D assisted cooperative NOMA scheme to improve the outage performance in downlink NOMA systems.The NOMA-strong users are considered to help weak ones with full-duplex D2D communications in this scheme.In [10],the problems of channel assignment and power control for D2D communications underlaying a NOMA-based cellular network was investigated,where the sum-rate of D2D links was maximized and the minimum rate requirements for cellular users using NOMA was guaranteed.The D2D aided cooperative relaying system(CRS) using NOMA (DC-NOMA) proposed in [11]can obtain higher achievable rate than that of CRS using NOMA or CRS using orthogonal multiple access.

The above researches about NOMA-based D2D communications all towards conventional D2D communications where two D2D users communicate directly.However,conventional D2D communications might not always be feasible in practice,as the direct link could be in deep fading due to poor transmission condition (e.g.shadowing,energy attenuation and poor access permission).To expand D2D coverage and enhance the applicability of D2D communications,relay-assisted D2D communication (also referred to as multi-hop D2D)has been envisaged as an increasing spectral-efficient technology[12,13].The work in [14]studies the maximum achievable transmission capacity in one-way relay-assisted D2D communications to guarantee the outage probability of both cellular and D2D links.The power allocation schemes maximizing the energy efficient of the relayaided D2D communications is provided to ensure the minimum data rate of the cellular link in [15].The performance in terms of throughput and end-to-end packet loss probability of dual-hop,two-way,and asymmetric D2D communications are investigated in[16].The work in[17]investigates the performance of a relay-based and network-coding-assisted multi-hop D2D communication system with various channel fading models and traffic models.

Although the integration NOMA with D2D communications is one of the active areas of research,only a very few work in the literature consider relay-assisted D2D communications.In this paper,we present a relaying D2D communications assisted cooperative relaying systems using NOMA (DRC-NOMA) which can increase spectrum efficiency using the combination of NOMA-based cooperative relaying systems and relaying D2D communications.Different from the model of connected D2D-enabled cellular systems in [11],in this new framework,the D2D users reuse the downlink spectral resources with the cellular users and a relay is used to forward the information of D2D user and cellular user.The DRC-NOMA presented in this paper can be regarded as including a CRS using NOMA and multi-hop D2D communications using the same relay,while the DC-NOMA in [11]is combine CRS using NOMA with conventional D2D communications.Compared to DC-NOMA,the DRC-NOMA can improve the achievable sum-rate in the conditions of long distances or poor channel between D2D users.In addition,an optimal power allocation strategy to achieve the maximum sum-rate is proposed.The main contributions of this paper can be summarized as follows:1)We put forward a new way that relay assisted D2D communications reuse the downlink spectral resources with the cellular users using NOMA.2) We study the ergodic sum-rate and derive the analytical expression for the proposed DRC-NOMA.3)We propose a simple but important power allocation strategy maximizing the sum-rate of DRC-NOMA.Analytical results are validated through simulation results.

The remainder of this paper is organized as follows.The system model of downlink DRC-NOMA is presented in Section II.The theoretical derivation of ergodic sum-rate of DRC-NOMA and an optimal power allocation strategy maximizing sum-rate are investigated in Section III.Numerical results based on theoretical derivation and system simulation are discussed in Section IV.Finally,the conclusion is presented in Section V.

II.SYSTEM MODEL

The system model of downlink DRC-NOMA in a single cell is shown in figure 1,where a base station(BS),a cellular user(CUE),a relay(RELAY)and a pair of D2D users (D1,D2) are considered and all nodes are equipped with a single antenna.In particular,there is no direct link between the D2D users due to channel condition limitations and the relay is introduced to serve both the cellular and D2D users.The system model can be considered as combining a cooperative relaying system with relay-assisted D2D communications using the same relay.In the scenario,CUE is far away from the BS,while other users are relatively close to the BS.NOMA downlink transmission is to be used since users have very different channel state information.

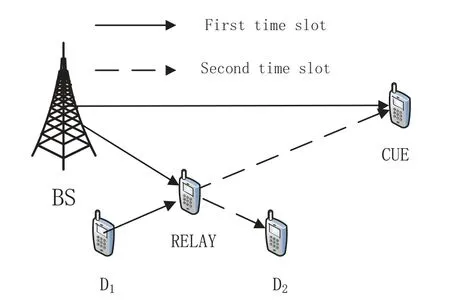
Figure1.System model of NOMA-based D2D relay communications.

For all the links,we assume independent Rayleigh fading channels and perfect SIC receivers.The BS transmits signaldirectly androm the relay node to the cellular user,andtransmit signaltorom the relay at the same time.The relay node uses DF mode and works in half-duplex mode.The transmission process is divided into two consecutive equal length time slots.The BS transmits a signalto the CUE and relay during the first time slot,wherePBdenotes the transmit power of the BS,aidenotes the power allocation coefficient of the symbolxi,andi=C1,C2.From the viewpoint of the BS,CUE is assumed as a NOMA far user,that is,CUE has the weaker channel condition.Thus we should allocate more power to the symbolxC1,and therefore,a1＞a2,wherea1+a2=1.At the same time,D1transmits a signalto the relay,wherePD1indicates the transmit power of the D1.During the second time slot,the relay broadcasts another signalto the CUE and the D2D receiver D2,wherePRdenotes the transmit power of the relay,andbiindicates the power allocation coefficient of the symbolxi,wherei=C2,D.From the relays point of view,CUE is assumed as the NOMA far user,andb1＞b2,whereb1+b2=1.

In this paper,the subscriptsB,C,R,D1,D2denote BS,CUE,relay,D1,and D2,respectively.We assume that frequency flat block fading channels ishXY,andhXY ∼CN(0,βXY) represent the channel coefficients betweenX ∈{B,R,D1}andY ∈{R,C,D2},whereβXYmeans the average channel gain.Without loss of generality,it is assumed thatβBR ＞βBCandβRD2＞βRC.The received signals at the relay and CUE in the first time slot can be respectively expressed as

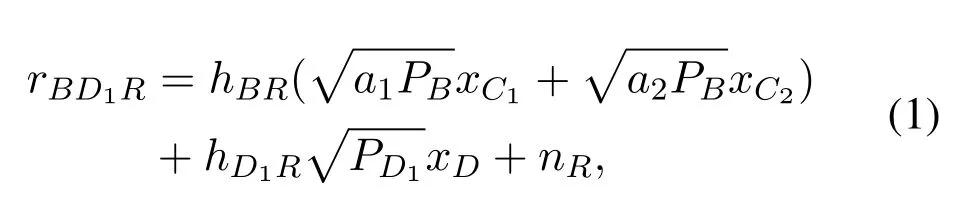
and

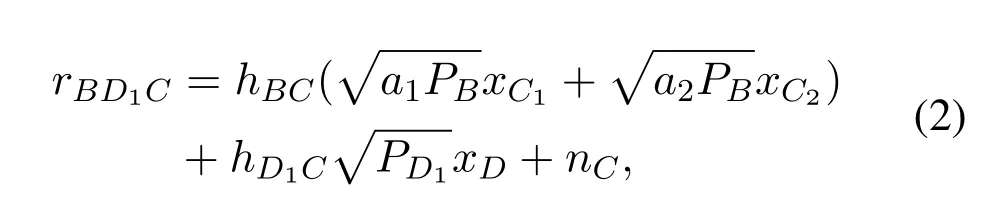
wheren(.)∼CN(0,σ2) is a complex additive white Gaussian noise (AWGN) at each receiver.As is well-known under normal circumstances,the transmit power of the BS is greater than the transmit power of the D1.So the relay firstly decodes symbolxC1by treating symbolxC2andxDas noise,and then acquire symbolxC2andxDfrom (11) by using SIC.Thus,the received signal-to-interference plus noise ratios(SINRs)for symbolsxC1,xC2,andxDat the relay can be respectively given as

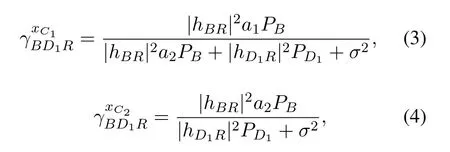
and

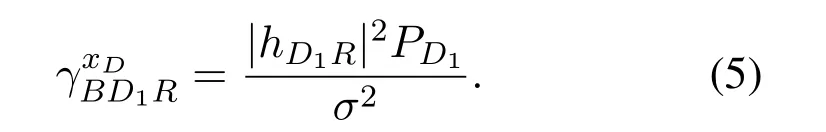
On the other hand,CUE acquire symbolxC1by treating symbolxC2andxDas noise from(2).The received SINR for symbolxC1at CUE can be given by

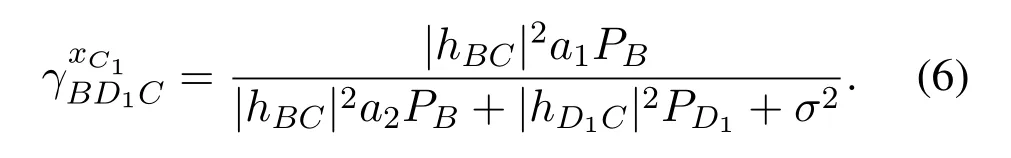
During the second time slot,the received signals at the D2and CUE can be respectively expressed as

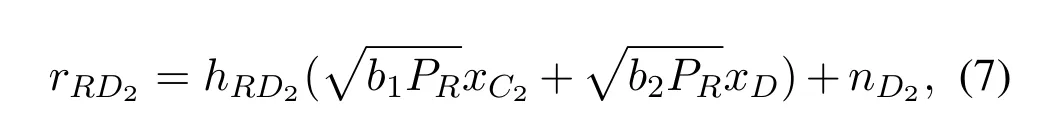
and

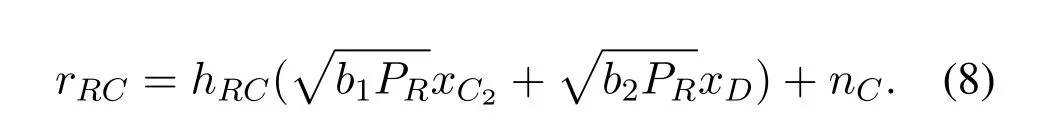
By treating symbolxDas noise,D2decodes symbolxC2and then cancels it using SIC to achievexDfrom (7).The received SINRs at D2forxC2andxDare respectively acquired as

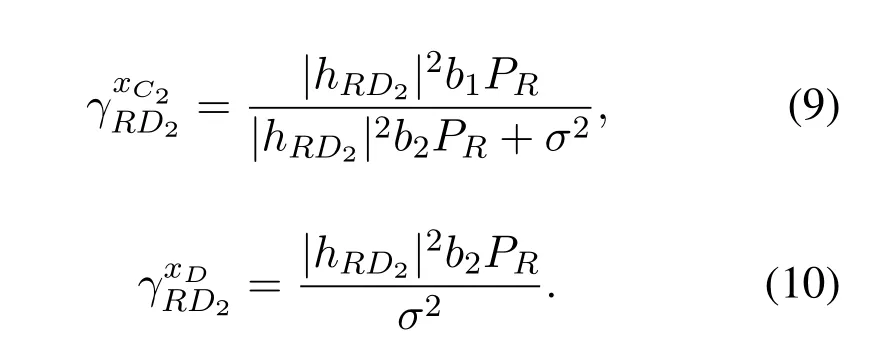
When decodingxC2from (8),CUE treats symbolxDas noise.The received SINR for symbolxC2at CUE is given by

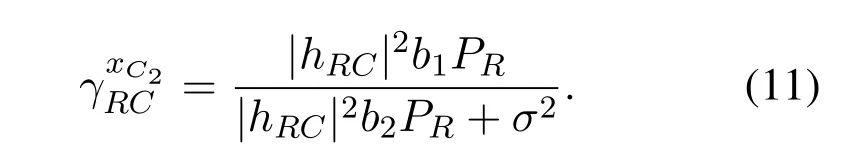
When the expressions of received signals and SINRs are obtained,the achievable rate of each symbol can be obtained.Since the relay should decodexC1for SIC,the achievable rate associate withxC1can be acquired from(3)and(6)as

Considering that the rate of the weakest link dominate the achievable rate of DF relaying,D2should decodexC2for SIC,the achievable rate associate withxC2is obtained from(4),(9)and(11)as

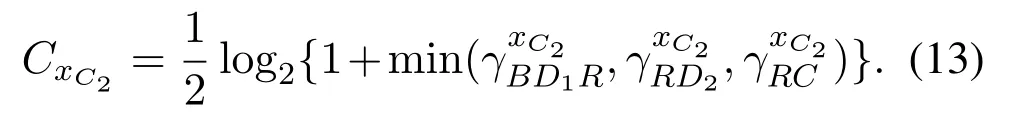
Because the transmission of D2D also uses the DF relay,the achievable rate associate withxDis obtained from(5)and(10)as

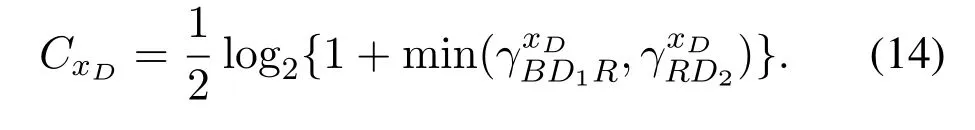
III.PERFORMANCE ANALYSIS

The ergodic sum-rate of this system is given bywhere the first two terms denote the achievable rate of the CUE from BS directly and relayaided respectively,the last term denotes that of D2D user.LetandρD1=be the transmit SNRs for the BS,relay and D1respectively.

3.1 The Rate of Symbol XD

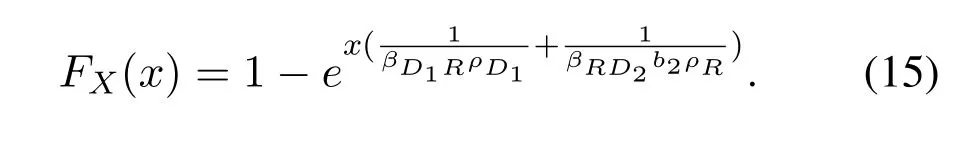
We can find thatXobey exponential distribution with the parameter 1/(1/(βD1RρD1) + 1/(βRD2b2ρR)).

From[18],is obtained as

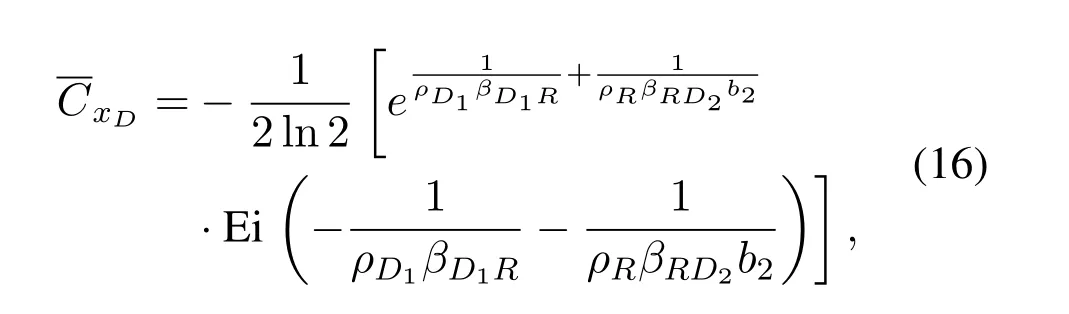
3.2 The Rate of Symbol XC2

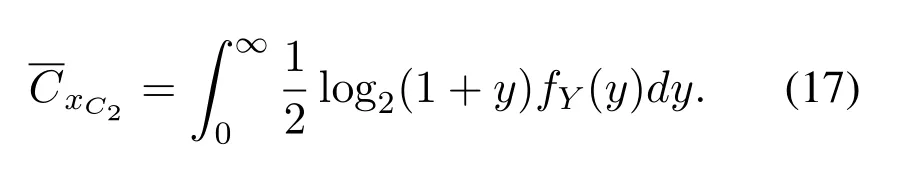
For a sufficiently largeρR,

Then the PDF ofYis obtained as

wherea=ρD1βD1R,andb=ρBa2βBR.

Thenis approximated as

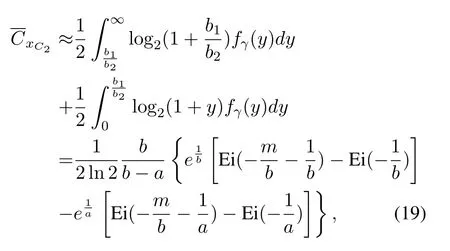
wherem=b1/b2,a=ρD1βD1R,andb=ρBa2βBR.

3.3 The Rate of Symbol XC1

First,the CDF ofY1is obtained as

Taking the derivative ofFY1(y),the CDF ofis obtained as

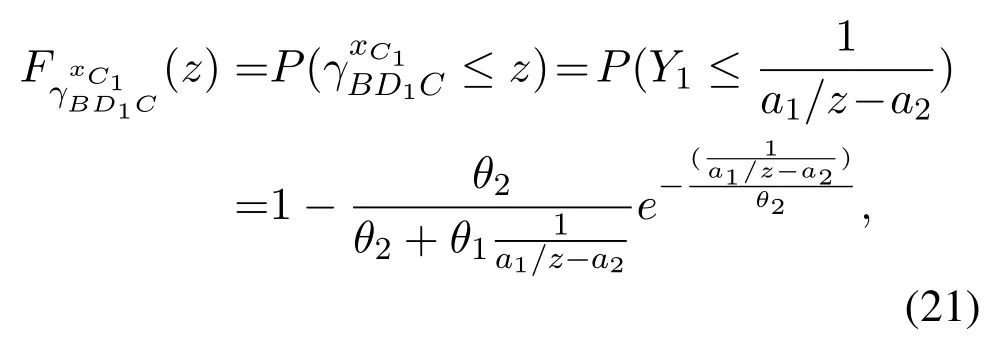
where 0＜z ＜a1/a2.

Similarly,we can obtain the CDF ofLettingbecause of the independence ofthe CDF ofTis obtained as

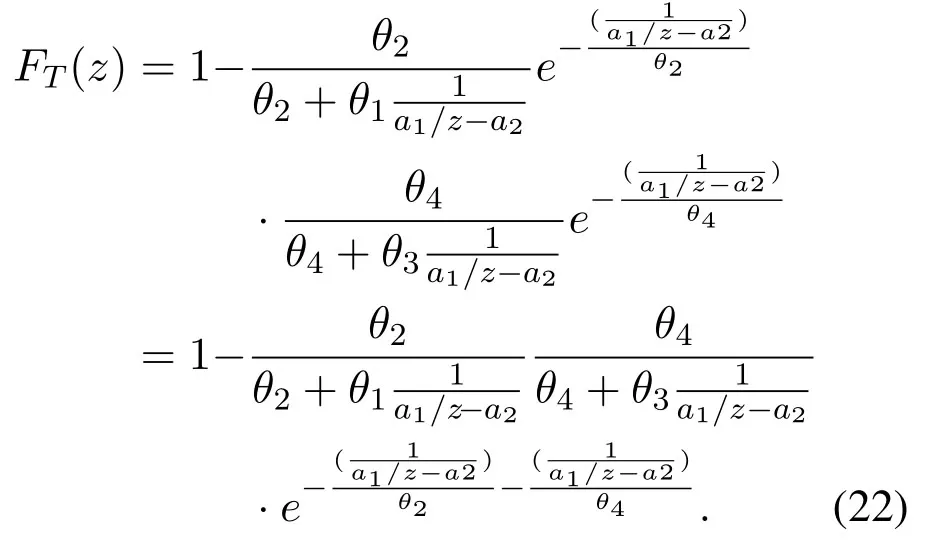
Using(16),is obtained as

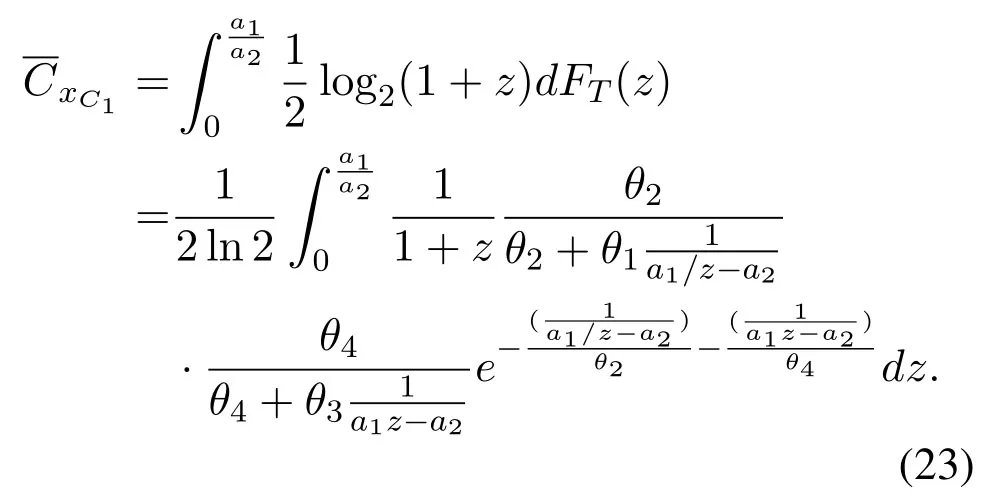
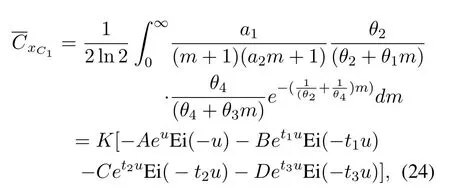
From (16),(19) and (24),the ergodic sum-rateof the DRC-NOMA is then obtained.By numerical calculation,the analytical results of the ergodic sum-rate can be achieved,and the simulation results will verify the accuracy of the closed-form expression in the next section.

3.4 Power Allocation

In this subsection,we focus on the optimal power allocation of the DRC-NOMA.The ergodic sum-rate achieved in the above section can be used to determine the power allocation coefficientsa2andb2.We investigate this particular optimization maximizing the ergodic sum-rate as follows

The closed-form solutions of asymptotically optimal solutionsa2andb2are difficult to obtain.However,the numerical solution of the asymptotically optimal solution can be calculated efficiently by the following iterative method.First,given thatb2is fixed to an initial value,the optimala2(b2)=arg max0＜a2＜0.5Csumcan be obtained via one-dimensional search.Then,given thata2is fixed toa2(b2),the optimalb2(a2)=arg max0＜b2＜0.5Csumalso can be obtained via onedimensional search.Repeating the above steps until the difference in the value of two successive rates less than a given small value.At this time,thea2andb2obtained by the iterative method are sub-optimal power allocation coefficients.By using the theoretical expression of the ergodic sum-rate,the computational complexity can be reduced greatly.

IV.NUMERICAL RESULTS

In this section,the analytic results obtained in the previous Section are compared with those of Monte Carlo simulation to verify the accuracy.Specifically,the simulation results are given by Monte-Carlo averaging over 105independent channel realizations.For comparison purpose,simulation parameters refer to the parameters in[11],whichβBC=0.1,βBR=1.5,βRC=0.5,βD1R=2,βRD2=2,βD1C=0.1,w1=0.2,w2=0.2,andw3=0.6.For the sake of simplicity in simulation,we assume the relay node is located halfway between D1and D2.

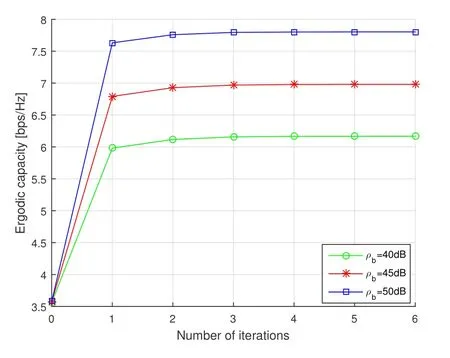
Figure2.The ergodic sum-rate of the proposed DRCNOMA with respect to number of iterations.

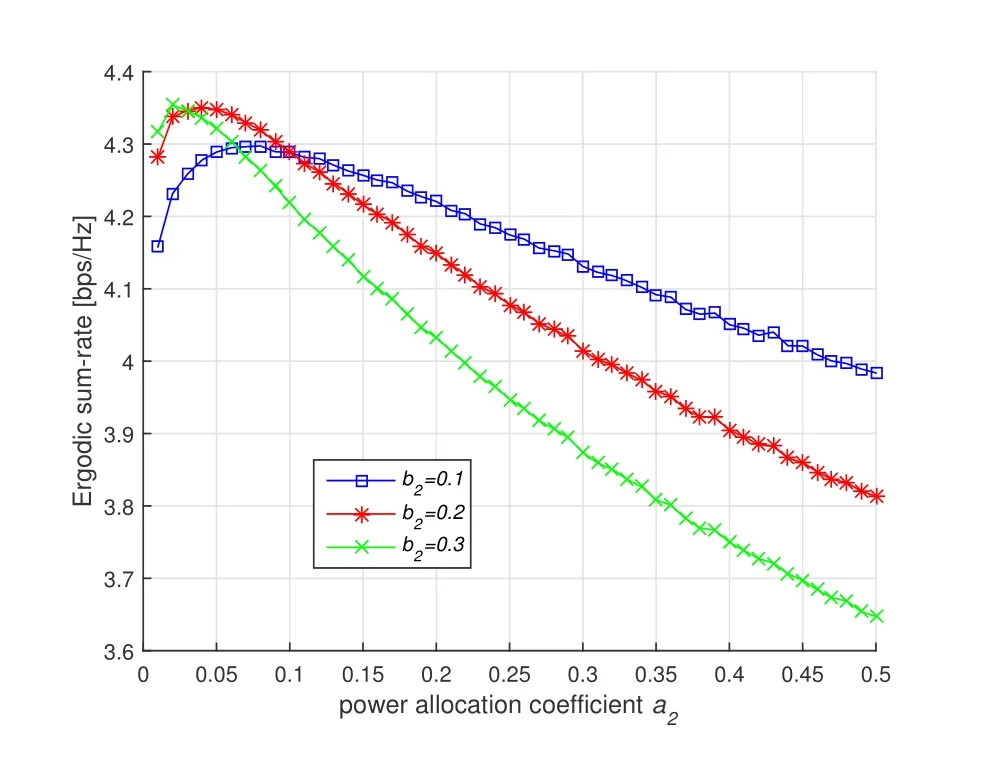
Figure3.The ergodic sum-rate of the proposed DRCNOMA with respect to power allocation coefficients a2.

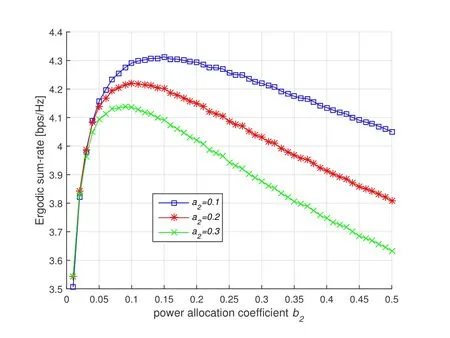
Figure4.The ergodic sum-rate of the proposed DRCNOMA with respect to power allocation coefficients b2.

The optimization problem of the ergodic sum-rate in above section can be solved effectively by iterative method.The convergence of the iterative power allocation is simulated as shown in figure 2.The figure shows the ergodic sum-rate of the proposed DRC-NOMA with respect to number of iterations.As shown in figure 2,the ergodic sum-rate is monotonically increased after each iteration and stabilized after four iterations,which indicates that the iterative algorithm is convergent and the convergence rate is very fast.The optimal power allocation strategy maximizing ergodic sum-rate based on the proposed analysis results has low complexity.

Figure3 and figure 4 show the ergodic sum-rate of the proposed DRC-NOMA with respect to power allocation coefficientsa2andb2respectively.In the figure 3,whenb2takes different values,with the increase ofa2,the change of sum-rate is the same,all of which increase first and then decrease.The increase ina2means that less power is allocated to CUE and more power to relay.The first term of ergodic sumrate is decrease and the second term is increase with the increase ofa2.In the former stage of thea2increase,the first term decrease slowly and the second term increases quickly inducing the increase of the ergodic sum-rate.In the latter phase of the increase ina2,the corresponding changes are opposite and the ergodic sum-rate decreases.Therefore,whenb2is fixed,there is an optimala2to maximize the sum-rate.Similarly,in the figure 4,whenb2increases,the sum-rate increases at first and after reaching a peak,then it decreases withb2further increases.Hence,there also is an optimalb2to maximize sum-rate.Figure3 and figure 4 indicate that a pair of optimal value ofa2andb2exist that maximize the ergodic sum-rate.

Figure5 compares the ergodic sum-rate for different power allocation strategy with the transmit SNR of BS.The figure verifies that the analytic curve is exactly matched with the simulated one.The ergodic sumrate using the proposed optimal power allocation strategy increases greatly with the increases of the transmit SNR of BS.The sum-rate using equal power allocation strategy approach to a constant value when the transmit SNR of BS increase.It is clearly observed that the proposed optimal power allocation strategy attains remarkable performance gain over the equal power allocation strategy for DRC-NOMA.Figure6 shows the ergodic sum-rate with transmit SNR in the relay.The figure also verifies that the analytic curve match with the simulated one exactly in the high SNR situation.It is also well matched in low and moderate SNR situation.The ergodic sum-rate increases with the increases of the SNR of the relay transmission.Similar to figure 5,the proposed optimal power allocation strategy has better performance.From the two figures,we can find that when the transmission power is large enough,increasing the transmission power in BS is better than it in the relay.

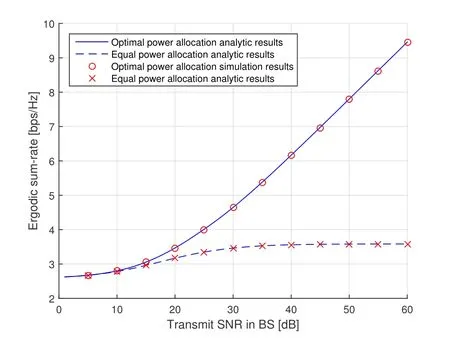
Figure5.The ergodic sum-rate of optimal power allocation and equal power allocation with respect to the transmit SNR of BS.

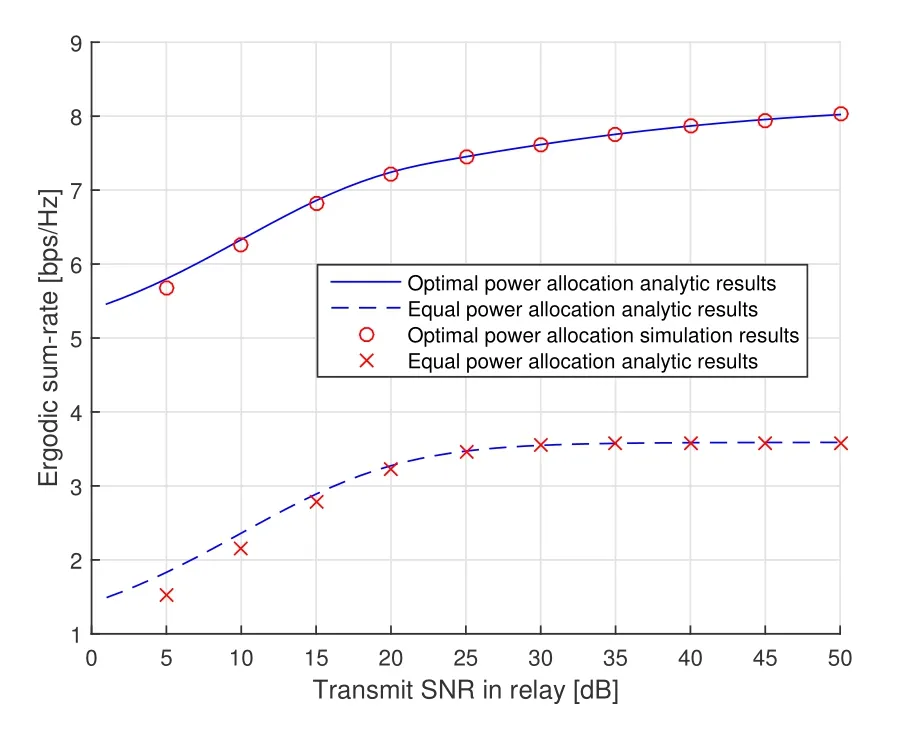
Figure6.The ergodic sum-rate of optimal power allocation and equal power allocation with respect to the transmit SNR of relay.

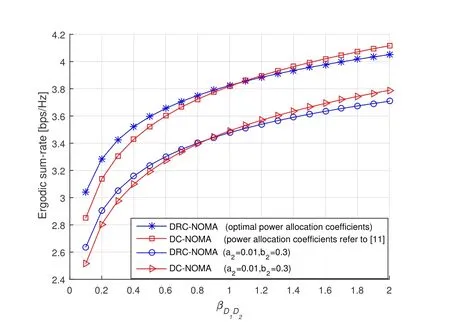
Figure7.The ergodic sum-rate of DRC-NOMA and DCNOMA with respect to average channel gain between D1 and D2,βD1D2.

Figure7 illustrates the ergodic sum-rate of proposed DRC-NOMA and DC-NOMA in [11]versus average channel gain betweenD1andD2,that isβD1D2.As shown in figure 7,both ergodic sum-rate of DRCNOMA and that of DC-NOMA increase monotonically asβD1D2increases.From the figure,we also see that the proposed optimal power allocation strategy for DRC-NOMA have better performance than that with the constant coefficients of power allocation.Whatever the power allocation coefficients are,the ergodic sum-rate of proposed DRC-NOMA is better than that of DC-NOMA in the case ofβD1D2＜1,whereas whenβD1D2increases,DC-NOMA has better performance.The smallβD1D2indicates that the distance between D2D pair is large or the D2D link experiences severe interference.Hence,the proposed DRCNOMA can improve the ergodic sum-rate compared to DC-NOMA when the channel condition is poor.

V.CONCLUSION

In this paper,we have analyzed the performance of DRC-NOMA by deriving the closed-form expression of the ergodic sum-rate.Moreover,an optimal power allocation strategy maximizing ergodic sum-rate was also proposed,which attains the remarkable performance gain over the equal power allocation strategy.The simulation results show that the analysis results derived in this paper are in perfect agreement with the Monte Carlo simulation results,and the DRC-NOMA is able to get better sum-rate than DC-NOMA when the average channel gain betweenD1andD2is small.

ACKNOWLEDGMENT

This work was supported in part by the National Natural Science Foundation of China under Grant 61701201,U1805262,61871446 and 62071247,the Natural Science Foundation of Jiangsu Province(No.BK20170758),Six talent peaks project in Jiangsu Province.