Fully Connected Feedforward Neural Networks Based CSI Feedback Algorithm

Ming Gao,Tanming Liao,Yubin Lu

School of Telecommunication Engineering,Xidian University,Xi'an 710071,China

Abstract:In modern wireless communication systems,the accurate acquisition of channel state information (CSI) is critical to the performance of beamforming,non-orthogonal multiple access (NOMA),etc.However,with the application of massive MIMO in 5G,the number of antennas increases by hundreds or even thousands times,which leads to excessive feedback overhead and poses a huge challenge to the conventional channel state information feedback scheme.In this paper,by using deep learning technology,we develop a system framework for CSI feedback based on fully connected feedforward neural networks(FCFNN),named CF-FCFNN.Through learning the training set composed of CSI,CF-FCFNN is able to recover the original CSI from the compressed CSI more accurately compared with the existing method based on deep learning without increasing the algorithm complexity.

Keywords:massive MIMO;CSI feedback;deep learning;fully connected feedforward neural network

I.INTRODUCTION

AS one of the critical candidate technologies of 5G wireless communication[1],massive MIMO can further improve the transmission efficiency and capacity of wireless communication systems and effectively reduce the interference between users and the energy consumption of the receiver or transmitter by deploying a large number of antennas at the base station(BS)side[2].However,to fully utilize the potential gains of massive MIMO,knowledge of channel state information (CSI) at the BS is essential.For example,many works about NOMA have assumed perfect CSI or the order of the instantaneous channel gain which can obtained from CSI feedback [3-5].However,imperfect CSI will seriously affect the performance of NOMA system [6-8].Due to the rapid increase of feedback overhead in massive MIMO systems,the conventional CSI feedback methods are difficult to apply to massive MIMO systems.As a result,many researches have been motivated to reduce the CSI feedback overhead in massive MIMO systems [9-13].In these efforts,[9-12]mainly uses the spatial or temporal correlation of the massive MIMO system to reduce the feedback overhead.Specifically,these methods design the algorithm based on the idea of compressed sensing (CS),which converts the channel matrix into a sparse vector that can be sparsely represented on some orthogonal basis.Then,the sparse vector is compressed and reconstructed so as to reduce the feedback overhead.However,in practice,the sparse vector of the channel matrix is only approximately sparse on certain orthogonal basis,such as two-dimensional discrete Fourier transform(2D-DFT)and two-dimensional discrete cosine transform (2D-DCT).This insufficient sparsity makes it difficult for the recovery algorithm in CS to recover the channel matrix accurately from the sparse vector.

In [13],a novel CSI feedback scheme based on deep learning is proposed.The compression and reconstruction process of channel matrix is fulfilled by a neural network called CsiNet,which is similar to the autoencoder [14].By learning the characteristics of the channel matrix from the training set,this scheme can recover CSI with greatly improved reconstruction quality compared with existing CS-based methods.

In this paper,in order to further improve the reconstruction accuracy of the channel matrix,we consider using the fully connected-feedforward neural networks(FC-FNN)to build a CSI feedback network,named CF-FCFNN.Different from the CsiNet built by a convolution neural network (CNN) which is more suitable for image processing,CF-FCFNN built by FC-FNN can extract spatial features sufficiently,so as to further improve the reconstruction performance.The simulation results show that the reconstruction quality of CF-FCFNN is better than CsiNet.In addition,our proposed network architecture is comparable to CsiNet in terms of the algorithm runtime.

The rest of the paper is organized as follows.Section II provides the system model for CSI feedback we considered in this paper.Section III explains the architecture of CF-FCFNN and the deep learning algorithms we used in detail.Simulation results that verify the effectiveness of CF-FCFNN are presented in Section IV.Finally,Section V provides the conclusions.

II.SYSTEM MODEL

Consider a flat slow-fading downlink massive MIMO system withNttransmit antennas at a BS and a single receive antenna at a UE operating in the FDD mode.It is assumed that the UE can obtain a perfect downlink channel matrix by pilot-based training[15].The channel feedback model of single-user MIMO system is shown in Figure1.The system is operated in orthogonal frequency division multiplexing(OFDM)overNcsubcarriers.The received signal at the kth subcarrier can be expressed as follows:wherehk ∈CNt×1,xk ∈Candnk ∈ Cdenote the channel vector,transmit data symbol and additive noise of thekth subcarrier,respectively,wk ∈CNt×1denotes the beamforming or precoding vector designed by the BS based on the downlink CSI.By sequentially stackingNcchannel vectors,the channel matrix in the spatial-frequency domain is represented asH=[h1,h2,···,hNc]∈CNt×Nc.

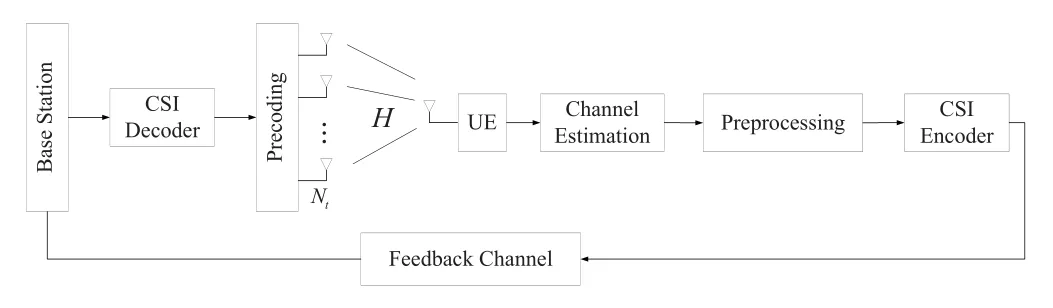
Figure1.The channel feedback model of single-user MIMO system.

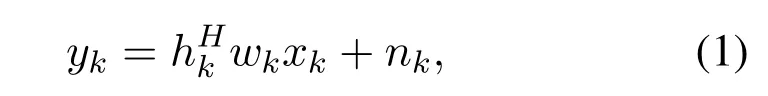
To reduce the feedback overhead and the complexity of the training set,we transform the spatial-frequency domain channel matrixHinto the angle-delay domain channel matrixH′through 2D-DFT as follows:

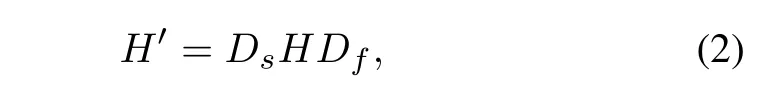
whereDs ∈CNt×NtandDf ∈CNc×Ncare both 2DDFT matrices.Due to limited multipath time delay,only the firstNc′(Nc′ ＜Nc)columns ofH′contain values.Therefore,within allowable range of accuracy,we can truncateH′intoH′′ ∈CNt×Nc′by retaining the firstNc′columns ofH′and removing remaining columns.The conversion fromHtoH′′is called preprocessing.In the research,we focused on designing the CSI encoder and the CSI decoder with excellent performance.The CSI encoder is used to transform the preprocessed complex channel matrixH′′into an Mdimensional(M ≪N,N=Ntotal=2×Nt×N′c)compressed vectorv,that is,

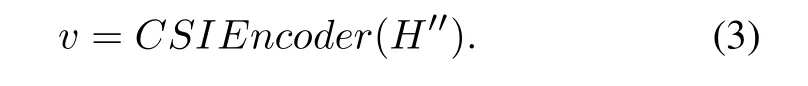
The data compression ratio is defined as follows:

Then the compressed vector v is sent to the BS through the feedback link by the UE.The CSI decoder is used to reconstructH′′from the compressed vectorvat BS,and the reconstructed channel matrix is represented bythat is,

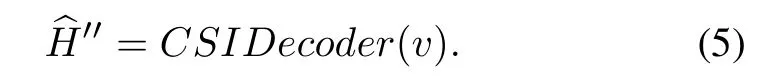
Finally,the original spatial-frequency domain channel matrixHis obtained by sequentially performing zero-padding and two-dimensional inverse discrete Fourier transform(2D-IDFT)onH′′.The encoding process and decoding process can be understood as the operation of compressing and reconstructing the complex channel matrixHrespectively.

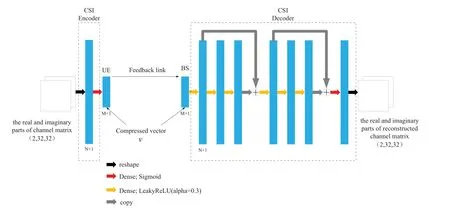
Figure2.The CSI feedback network based on the fully connected feedforward neural network

III.CF-FCFNN

We develop a CSI feedback network based on fully connected feedforward neural networks for CSI compression and reconstruction,named CF-FCFNN.The CSI feedback network based on the fully connected feedforward neural network is shown in Figure2.

CF-FCFNN consists of a CSI encoder and a CSI decoder,which are both built from neural networks.We exploit the CSI encoder to compress the complex channel matrix.The CSI encoder consists of an input layer and an output layer,which are fully connected by weighting values.We reshape the real and imaginary parts of the preprocessed complex channel matrixH′′into a vector with dimension ofN(N=2×Nt×Nc′),which serve as the input of the CSI encoder.The output of the CSI encoder is the compressed vectorv,which is obtained by reducing the dimensionMof the output layer.

Once the BS acquires the compressed vectorvfrom the UE through the feedback link,it uses the CSI decoder to reconstruct the original complex channel matrixH′′from the compressed vector.To fully extract the feature of the channel matrix,the CSI decoder is composed of an input layer,several hidden layers and an output layer.In this paper,we set the number of hidden layers to six.The input layer of the CSI decoder is composed ofMneurons that considers the compressed vector as input and outputs a vector of sizeN,which serves as an input of subsequent hidden layers.For the number of neural network layers in CF-FCFNN is directly related to performance of CF-FCFNN,we introduce the residual block of the deep residual network [16,17]into the CSI decoder to avoid the degradation of the performance caused by the depth of CF-FCFNN.Consider splitting the six hidden layers into two residual blocks,each of which consists of three hidden layers.In each residual block,there is a shortcut connection between the first layer and the third layer,so as to pass data flow to later layers directly.Besides,the activation function between the neural network layers of the two residuals blocks is set as the leaky version of a rectified linear unit(LeakyReLU),that is,

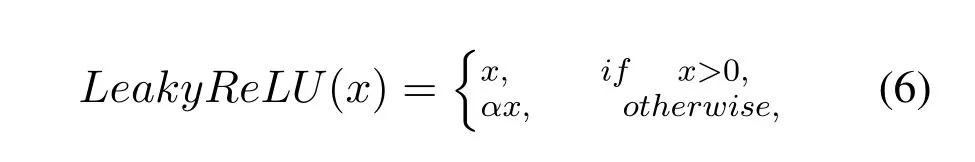
whereα ∈(0,1).After two residual blocks,the CSI decoder outputs the reconstruction ofH′′,which is represented by ︿H′′.

We determine the number of hidden layers and residual blocks of the neural network in CF-FCFNN through experiments.The experimental results show that six hidden layers and two residual blocks can achieve good recovery performance.Further increasing the hidden layers of CF-FCFNN or the number of residual blocks will not significantly improve the quality of recovery,but will increase the computational complexity.

In addition,in order to accelerate the convergence speed of network,we introduce batch normalization[18]to all layers in CF-FCFNN,which maps each layer of input to[0,1].Therefore,the output layer will map the output value to[0,1]using the sigmoid function in the CSI decoder.

To obtain all the weight and bias values of the CSI encoder and CSI decoder,we train them with end-toend learning methods of deep learning.We usef()to represent a well-trained CF-FCFNN,with CSI encoderfenand CSI decoderfde.When the input of CFN-FCFNN isH′′,the reconstructed channel matrix can be represented as follows:

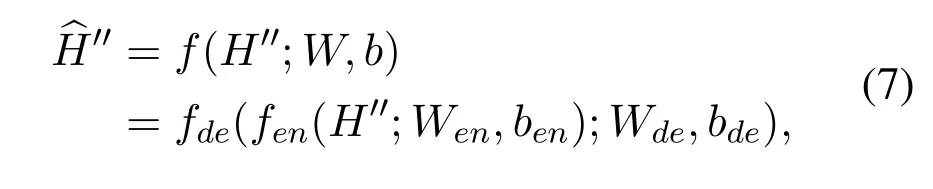
whereWenandbendenote the set of weights and biases for the CSI encoder respectively,Wenandbendenote the set of weights and biases for the CSI decoder respectively.We choose Adam [19]as the optimized algorithm for updating the set of parameters,and use the mean square error(MSE)as the loss function,which is defined as:

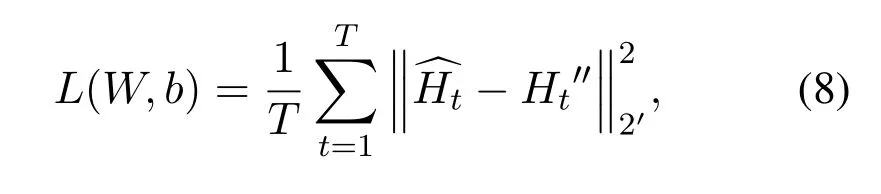
whereTis the number of samples in the training set,‖·‖2is the Euclidean norm.

IV.SIMULATION RESULTS AND ANALYSIS

In this section,we describe the detailed setup of our experiments and compare our approach with existing deep learning-based approaches.Referring to the default settings for all parameters in [20],we generate channel matrices under two scenarios through the COST 2100 channel model.We use uniform linear array(ULA)withNt=32 andNc=1024 subcarriers.In the preprocessing of the spatial-frequency channel matrix,we only retain the first 32 columns ofH′toobtainH′′with dimension of 32×32.The training,validation and testing sets contain 100000,30000,and 20000 samples for offline training or online testing respectively.The epochs,learning rate and batch size are set as 1000,0.001,and 200,respectively.The alpha of LeakyReLU function is set as 0.3.The performance of the network architecture is measured by the normalized mean square error(NMSE)and the cosine similarity[13].The difference between the reconstructed channel matrix ︿Hand original channel matrixHis quantified by NMSE,which is defined as follows:

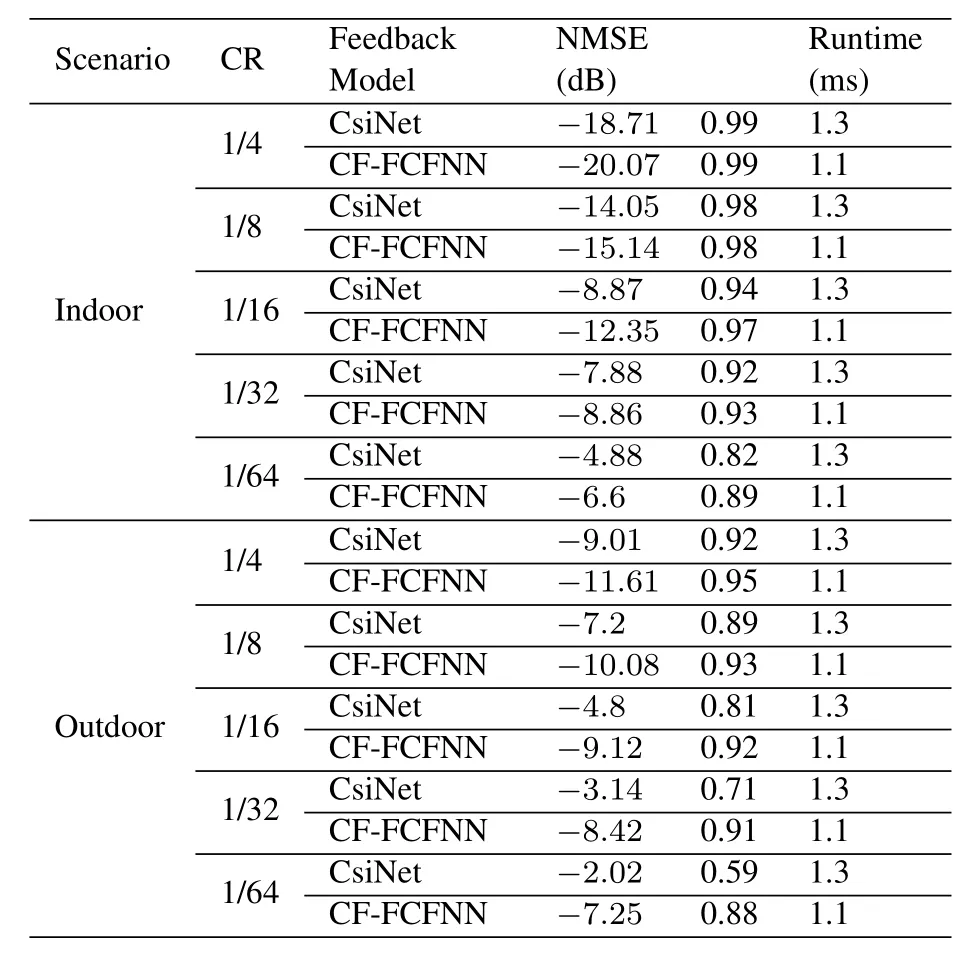
Table1.NMSE in dB,Cosine Similarity and Runtime in ms.

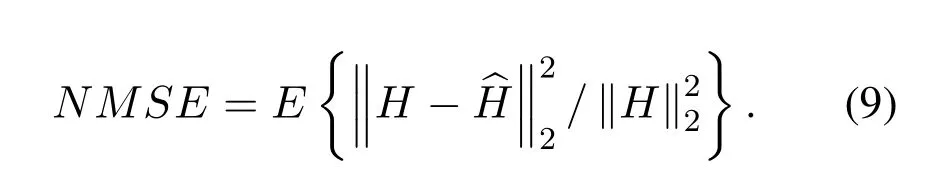
The cosine similarity is defined as follows:

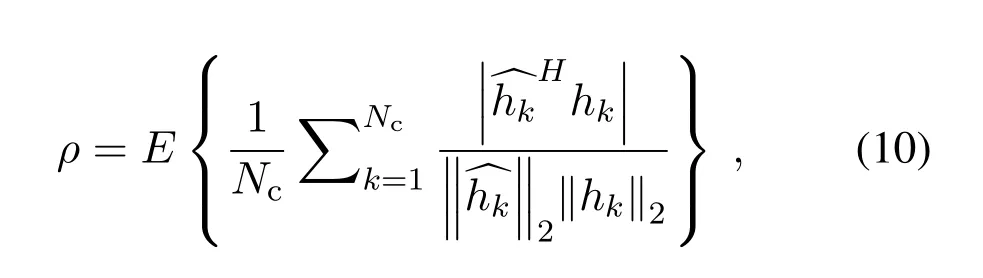
We performed the experiments withCRvalues of 1/4,1/8,1/16,1/32,and 1/64,respectively.In addition,CsiNet and CF-FCFNN are trained and tested on the Nvidia GeForce GTX 1050 Ti GPU.In all experiments,all parameters of CsiNet follow their default setting in[13].The corresponding NMSE,ρand runtime of CsiNet and CF-FCFNN for eachCRvalue are summarized in Table1.

It can be seen from the table that the performance of CF-FCFNN is significantly better than CsiNet with differentCRvalues,especially in outdoor scenarios.For example,the reduction of CR will cause distortion to increase,therefore,ρwill decrease.With the reduction ofCR,the performance ofρof CF-FCFNN scheme is obviously better than CsiNet scheme.Furthermore,the online runtimes of the two networks are almost the same.Therefore,we conclude that CFFCFNN based on fully connected feedforward neural networks can significantly improve the channel reconstruction quality without increasing the time complexity.

V.CONCLUSION

In this paper,we propose a novel CSI feedback framework CF-FCFNN by using the fully connected feedforward neural networks.The framework can significantly improves the channel reconstruction quality without increasing the time complexity.For accurate CSI can avoid error propagation effectively in SIC receivers in NOMA system,it is foreseeable that better system performance can be obtained using our CSI feedback scheme.Furthermore,based on the existing CSI feedback framework,we believe that if the time correlation of channels was taken into account,the performance of channel matrix reconstruction would be further improved[21].Therefore,we leave the exploitation of the time correlation across fast-varying channels as a topic for future researches.

ACKNOWLEDGEMENT

This work was supported by the Key Research and Development Project of Shaanxi Province under Grant no.2019ZDLGY07-07.