Erasure-Correction-Enhanced Iterative Decoding for LDPC-RS Product Codes

Weigang Chen,Ting Wang,Changcai Han,Jinsheng Yang

School of Microelectronics,Tianjin University,Tianjin 300072,China

Abstract:Low-density parity-check (LDPC) codes are widely used due to their significant errorcorrection capability and linear decoding complexity.However,it is not sufficient for LDPC codes to satisfy the ultra low bit error rate (BER) requirement of next-generation ultra-high-speed communications due to the error floor phenomenon.According to the residual error characteristics of LDPC codes,we consider using the high rate Reed-Solomon (RS) codes as the outer codes to construct LDPC-RS product codes to eliminate the error floor and propose the hybrid error-erasure-correction decoding algorithm for the outer code to exploit erasure-correction capability effectively.Furthermore,the overall performance of product codes is improved using iteration between outer and inner codes.Simulation results validate that BER of the product code with the proposed hybrid algorithm is lower than that of the product code with no erasure correction.Compared with other product codes using LDPC codes,the proposed LDPC-RS product code with the same code rate has much better performance and smaller rate loss attributed to the maximum distance separable(MDS)property and significant erasure-correction capability of RS codes.

Keywords:low-density parity-check codes;product codes;iterative decoding;Reed-Solomon codes

I.INTRODUCTION

Error correction code has been considered as one of the key technologies for next generation high-through put,high-reliability information systems such as highspeed fiber-optic communication,high-density magnetic storage [1,2].The low-density parity-check(LDPC) code is widely used in these fields,as it not only has superior performance,but also can be decoded using parallel iterative decoding algorithm to support high throughput[3,4].However,when LDPC codes operate in the high signal-to-noise ratio (SNR)region,the bit error rate (BER) curve often changes its slope,manifesting the so-called error floor phenomenon [5,6].Specifically,LDPC codes exhibit“waterfall”curves as the error rates drop very fast after a certain SNR threshold.It should be noted that,at the bottom of the“waterfall”region,the slope of the curve often decreases dramatically,which is referred to as the error floor (the bottom of the “waterfall”) mentioned above.Therefore,the effectiveness of LDPC code is reduced in communication systems requiring extremely high reliability.

The error-floor performance of LDPC codes is related to the sub-optimality of iterative decoding and the error-prone substructures (EPSs) such as nearcodewords,trapping sets (TSs),pseudo codewords,and absorbing sets(ASs)[7-10].For the LDPC code with a long code length,although the performance approaches the Shannon limit,the error floor still exists.The methods to improve the error floor can be mainly divided into two categories.The first is to optimize the structure of LDPC codes or to modify LDPC decoding algorithms[11].For example,a modified progressive edge-growth construction algorithm is proposed and verified via analyzing the constructed Tanner graphs in [12].The combination of LDPC codes over GF(q)withq-ary modulations for bandwidth efficient transmission over AWGN channel is studied and the design of the codes is considered in[13].However,the design complexity brought by these methods is high.The second is to construct compound codes,such as concatenated codes or product codes [14-16].For example,the LDPC-BCH concatenated code is used in the digital video broadcasting satellite-2nd generation(DVBS2)standard to eliminate the error floor[17].For polar codes have been shown to be a family of capacity achieving codes,the LDPC-polar concatenated code is presented to obtain superior performance and a complete hardware architecture of parallel encoding and decoding scheme is also proposed [18,19].Product codes have been introduced as an efficient mechanism for constructing long codes using two or more sets of shorter linear block codes [20-22].The References[23-26]give the application of product code in highspeed fiber-optic communication system and magnetic tape storage.By using algebraic code or other errorcorrecting codes as the outer code and LDPC codes as inner codes to form the product code,the error floor of LDPC codes can be effectively lowered[27-30].The following methods are used to further optimize the performance of product codes [31,32].By adopting post-processing technique,the impact of stall pattern on error floor can be effectively reduced [33].Additionally using an ensemble weight enumerator analysis to construct quasi-cyclic generalized LDPC code also leads to lower error floor [34].For LDPC-RS(Reed-Solomon) product codes,the “error estimation” and“soft value modification”techniques are combined to form a “turbo-like” hybrid iterative decoding to improve the error correction performance [35].In [36],the product code is devised using LDPC code as the inner code,and the high-rate BCH code as the outer code,which can achieve quite low BER with little rate loss.However,in all these schemes,erasurecorrection capability is not exploited.

In this paper,we construct product codes using RS codes with high code rate as the outer code and LDPC codes as the inner code,aiming at decreasing the rate loss and reducing the error floor.Considering the relatively large minimum distance of the LDPC code,RS codes can achieve the least code rate loss when using erasure-correction schemes based on the fact that most of the residual errors of the LDPC codes are detectable.According to the check results of LDPC codewords,the location information of erasures can be provided effectively to further take advantage of the erasure-correction capability of the outer code.For the outer code,we propose the hybrid error-erasurecorrection decoding algorithm to correct the residual error after LDPC decoding.The erasure-correctionenhanced scheme is expected to full exploit the errorerasure-correction capability of RS codes.Furthermore,iterative decoding is presented to enhance the overall performance of the product code.

Our contribution in this paper can be summarized in two points.On the one hand,the proposed iterative scheme and also the proposed product code construction are actually a tradeoff of the performance and complexity.The proposed product code scheme can effectively reduce the error floor of LDPC code.Compared with LDPC codes with the same overall code length and code rate,although the performance is not the optimal,the proposed product code has lower memory complexity and routing complexity in codec implementation.On the other hand,the erasurecorrection capability of the outer code is fully utilized to improve the performance in the proposed scheme with little additional complexity.Apart from this,the proposed iterative decoding which can further optimize the performance also has low extra complexity.In brief,the product code and compatible erasurecorrection-enhanced iterative decoding are proposed to obtain very low BER,very high throughput and flexible parallel levels,though the schemes do not achieve the capacity-approaching performance compared with long LDPC codes of the same length.We present a pragmatic long coding scheme avoiding the implementation bottleneck of very long LDPC codes.

The remainder of this paper is organized as follows.Section II presents the analysis of the residual error characteristics.Section III details the proposed erasure-correction-enhanced iterative decoding scheme for LDPC-RS product codes.In Section IV,simulation results and analysis are reported.Section V concludes the paper.

II.RESIDUAL ERROR CHARACTERISTICS ANALYSIS FOR PRODUCT CODE DESIGN

This section mainly analyzes the residual error characteristics of LDPC codes,including the distribution of errors and the corresponding error detection capability[37].A case study of LDPC code in IEEE 802.16e standard[38]is considered.On the basis of error characteristics analysis,the selection of outer code rate and decoding algorithm is investigated for the product codes which can achieve extremely low BER.

Structures of concatenated codes or product codes with LDPC codes plus high-rate RS codes are shown in Figure1.Different from concatenated codes,the product code can be represented using a matrix,and each row of the matrix represents an inner LDPC codeword,one or more columns constitute an outer codeword.RS codes are maximum distance separable (MDS) codes and satisfy Singleton bound.For RS code with the code length ofnsymbols and the code rate ofk/n,the minimum hamming distance isdmin=n-k+1.Hence,RS code can serve as the best candidate to optimize the code rate of product code by taking advantage of the MDS property.Meanwhile,different from BCH code,RS codes are defined over Galois field GF(q) (q /=2 ) and symbols rather than bits are used for code construction.Compared with BCH code,the performance of RS code with the same code length and code rate is more superior.Furthermore,for RS(n,k) code,the error-erasure-correction decoding algorithm can be used to correct (n - k)erasures or (n-k)/2 errors.The erasure correction scheme is fully exploited to obtain the optimal errorcorrection potential with the same parametersnandk.In this paper,RS code with code length ofn1symbols and code rate ofk1/n1is used as the outer code,and LDPC code having code length ofn2bits and code rate ofk2/n2is used as the inner code.We choose the RS codes over the Galois field GF(2m),and the code length isn1=2m -1 symbols,each symbol havingmbits.

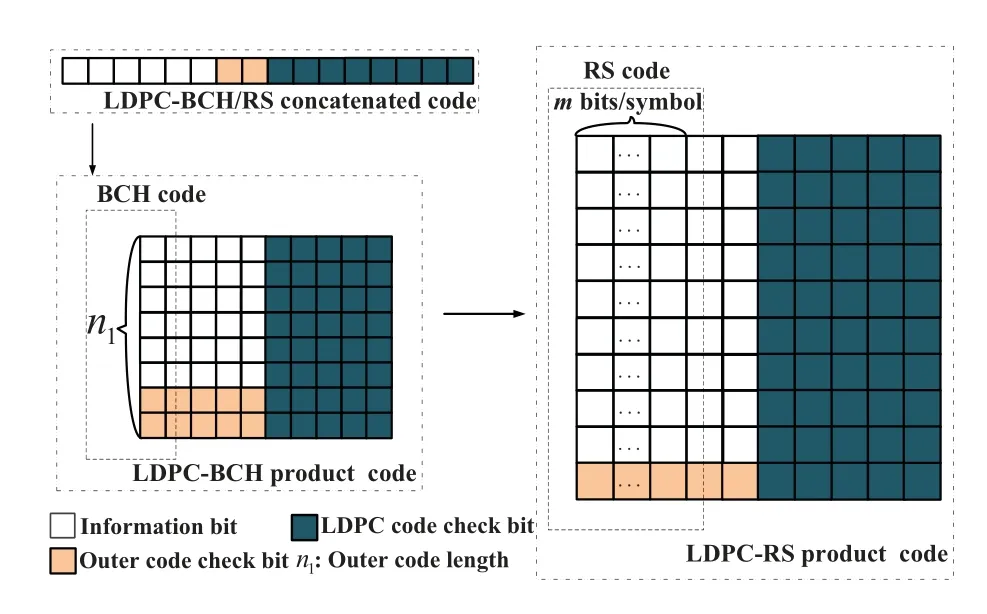
Figure1.Structures of product codes and concatenated codes with LDPC codes and high-rate block codes.

LDPC(576,288)code has been mentioned in IEEE 802.16e mobile WiMAX standard and was applied in many communication fields.Meanwhile,the related research about implementation has been presented and optimized.For optimized LDPC code with different code length and code rate,LDPC(576,288) code is representative and has similar characteristic.Therefore,LDPC code with the code rate of 0.5 and the code length of 576 bits is selected as an example for analysis.We use RS code with code length of 255 symbols as the outer code.The information part of each LDPC codeword can be decomposed into 288/8=36 symbols,each of which is included in a single RS codeword.Simulations are performed over additive white Gaussian noise (AWGN) channel with binary phase shift keying(BPSK)constellation.

Initially,the distribution of residual errors in the same position of successiven1LDPC codewords is analyzed.As mentioned above,the information bit of an LDPC codeword can be divided into 36 groups,and each group contains 8 bits.Considering the RS codeword over GF(28=256)is constructed by symbol and each symbol can be expressed as the 8-bit vector,the RS code over GF(256)is suitable to construct product code.It should be clear that for RS code over GF(2m),the commonly used code length is 2m -1.In addition,RS codes over GF(256) with the code length of 255 symbols has been widely used in space communications,optical fiber communication,data storage system and other communication systems.Thus,the corresponding RS code is very practical and is chosen to correct the residual errors.Here,we choosen1=255.At different SNRs,the relationship between the number of error symbols and its corresponding probability is shown in Figure2.It can be seen that as the number of error symbols increases,the occurrence probability decreases.Meanwhile,as the SNR increases,the probability decreases faster.This means that each outer codeword contains only few errors.Therefore,the outer code with a high code rate is enough to correct the residual errors of LDPC codeword.Secondly,the detectability of residual error symbols is analyzed.The decision method in this paper is simply to computeH·cT.If the result is not all zeros,a detectable error can be identified.The corresponding statistical results are shown in Figure3(a) and (b),respectively.With the increase of SNR,the probability of detectable errors and undetectable errors decreases.And the probability of undetectable errors is at least two orders of magnitude lower than that of detectable errors.Therefore,in the outer decoding process,according to the check results of LDPC codewords,the erasure location information of outer code can be obtained with exaggerated probability.

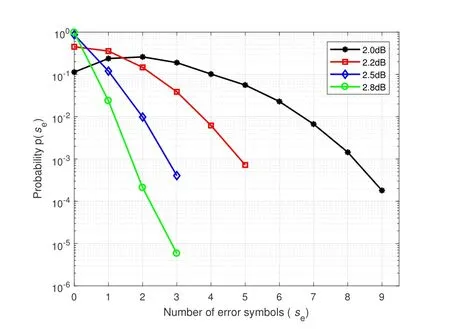
Figure2.Probability of the number of error symbols under different SNRs with 255 symbols in a group vertically.

III.ERASURE-CORRECTIONENHANCED ITERATIVE DECODING FOR LDPC-RS PRODUCT CODES

From the analysis above,it can be expected that the erasure-correction capability of RS code can be used to improve the overall performance.Therefore,we propose an erasure-correction-enhanced iterative decoding algorithm for LDPC-RS product codes.For RS codes,they can correct (n-k) erasures but only(n-k)/2 errors.Therefore,efficiently identify erasures and use the erasure-correction capability is quite important for the LDPC-RS construction.

3.1 The Iterative Decoding Procedures of Product Codes

The block diagram of proposed decoding algorithm is shown in Figure4.First,perform inner iterative decoding using the log-likelihood ratio (LLR) information expressed byL(0)and calculated as follows,

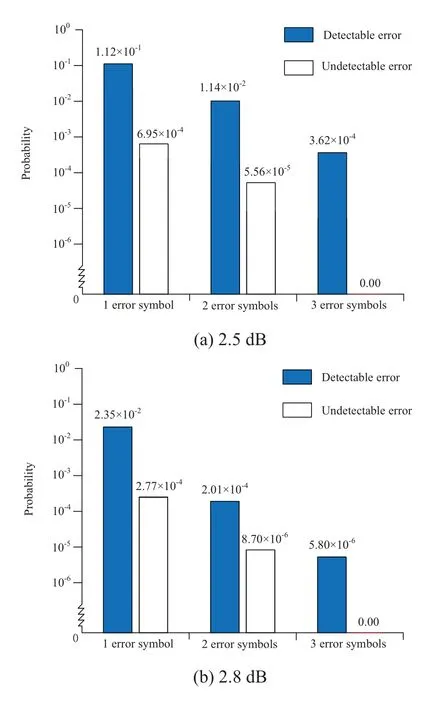
Figure3.Probability of occurrence of different error types when SNR is 2.5 and 2.8 dB.

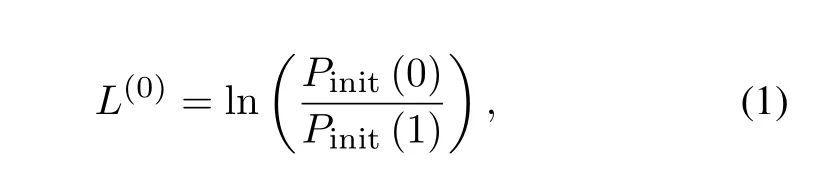
wherePinit(a) indicates the initial probability information that bit observed by the channel isa.The output of LDPC decoder is represented asyLDPC.

Next,in order to correct residual errors more effectively,mark the location ofH·yTLDPC/=0 as erasure.And the sequence of erasure location which is denoted aslocwill be formed as follows,

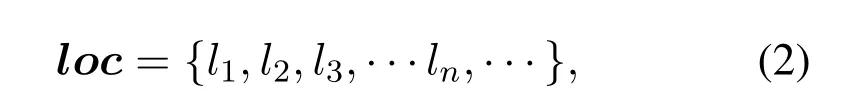
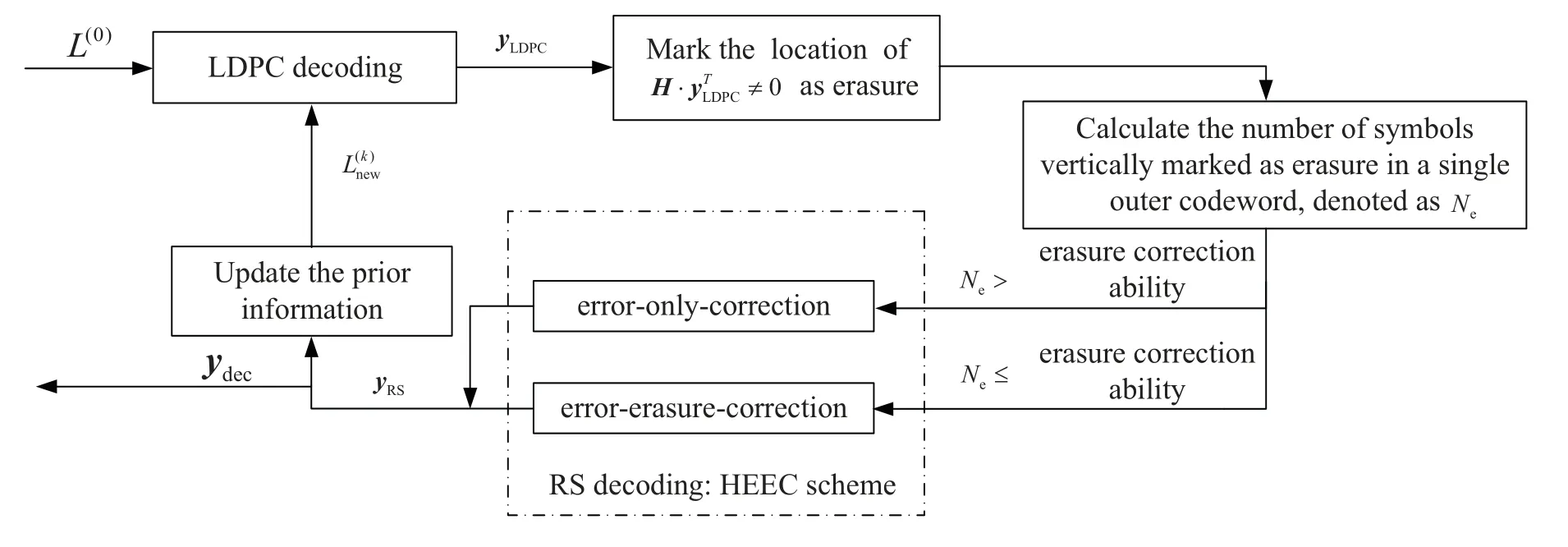
Figure4.Proposed erasure-correction-enhanced iterative decoding.

whereli(i=1,2,···,n,···) indicates the location information of thei-th erasure mark.During the procedure,if an LDPC codeword is marked as erasure,the location information of this LDPC codeword will be marked in all outer codewords in the product code,but real erasures may only exist in several outer codewords.It means that the outer codewords have false marked erasures for the symbols related to this LDPC codeword.

In order to take full advantages of the errorerasure-correction capability of RS code,we propose the hybrid error-erasure-correction (HEEC) decoding scheme for outer decoding.The number of symbols vertically marked as erasure in a single outer codeword,denoted asNe,should be calculated before performing outer decoding,and we have

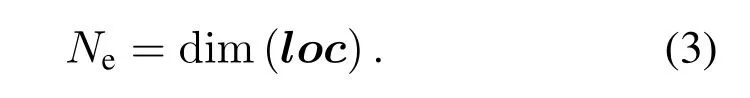
According to the evaluation ofNe,different decoding algorithms are used.IfNeis less than the erasurecorrection capability of the RS code,the error-erasurecorrection (EEC) decoding is performed.Otherwise,the sequence of erasure location is ignored and erroronly-correction (EOC) decoding is performed.Finally,the outer decoding resultyRSis obtained.

In order to further improve the performance,we propose a simple iterative decoding method.We update the prior information according to the posteriori probability obtained from inner decoding and the decoding result after outer decoding.The update rule can be expressed as follows

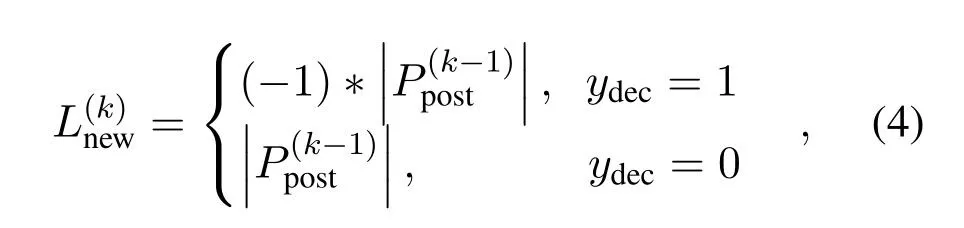
whererepresents the updated priori information,krepresents the iteration times,represents the posterior probability after LDPC decoding,andydecrepresents the RS decoding result.

In summary,we present a decoding scheme using enhanced erasure-correction for LDPC-RS product codes.The detailed iterative decoding procedures can be presented as Algorithm 1.

3.2 Complexity Analysis Of the Proposed Decoding Scheme

We present the complexity analysis in three aspects.First,we give the complexity analysis using hybrid error-erasure-correction decoding.Second,we show the complexity due to iteration.Finally,we compare the overall implementation complexity between the product code and a single LDPC code with the same code length.

3.2.1 The Complexity of the Hybrid Error-Erasure-Correction Decoding

The difference between the proposed hybrid decoding method and the error-only-correction decoding is mainly whether the erasure-correction capability of the RS code is utilized.

1) Complexity Increased Due to Erasure-Correcting Compared with error-only-correction decoding,there are four computations which need to be performed for error-erasure-correction decoding.The specifci calculation steps are shown in Table1,whereC[Pi(li)×Pj(lj)]indicates the complexity of polynomial multiplication over Galois feild between the polynomial with the maximum power ofliand the polynomial with the maximum power ofli,the power of the error location polynomial is denoted aste,andCerepresents the added complexity of calculating the erasure value.It can be observed in Table1 that the computational complexity has a direct relationship with the number of erasures.

Table1.The additional computation complexity for hybrid decoding.

The error-erasure-correction decoding is performed only whenNe＜ts,wheretsdenotes the erasurecorrection capability of RS code.Considering the high-rate RS code is used in the proposed product code,the value oftsorn1- k1is very small.Furthermore,it can be inferred thatNeis very small.It must be noted thattesatisfies the conditionte≤(n1-k1-Ne)/2.Considering the number of erasures is very small,the corresponding additional computation required for erasure-correction decoding is also very small.On the whole,the increased additional computation is very small for the proposed product code and can be ignored during the RS decoding

2)Complexity Decreased Due to Erasure-Correcting During the error-only-correction decoding,there is an important procedure which is used to obtain the error location.This procedure is achieved using(Berlekamp-Massey)algorithm and Chien search.BM algorithm is an iterative algorithm and its complexity is related to the number of iterations.Assuming that the complexity of each iteration is expressed asCBM,the total complexity of BM algorithm can be estimated as 2te× CBMand the polynomial multiplication is also existed in each iteration.Meanwhile,when 0＜ Ne＜ tsand the hybrid error-erasurecorrection decoding is performed,compared with the error-only-correction decoding,the value ofteis reduced by (n1-k1-Ne)/2 due to the existence of erasures and the corresponding computation of BM algorithm is also reduced.The reduced complexity can be written as(n1-k1-Ne)×CBM.

?

Apart from the above,whenNe=ts,the hybrid error-erasure-correction decoding only performs erasure-correction decoding.It doesn't need to perform the BM algorithm and the Chien search for obtaining the error location information.Therefore,the hybrid error-erasure-correction decoding reduces a lot of computations in this case.

In addition,forNethat satisfeis the conditionNe＞ts,the hybrid error-erasure-correction decoding has the same complexity as the error-only-correction decoding.

In summary,the hybrid error-erasure-correction decoding algorithm brings a little additional complexity and takes advantage of the erasure-correction capability.When only the erasure-correction decoding is performed,i.e.,there are only erasures in the received codewords,the hybrid decoding scheme even has smaller complexity than the traditional error-onlycorrection decoding.

3.2.2 The Computation Complexity of the Proposed Iterative Decoding

In this part,the complexity computation of the proposed iterative decoding is analyzed.

As can be seen from Eq.(4),there are only at mostn1×n2multiplications need to be performed for the information update of LDPC(n2,k2)-RS(n1,k1)product code in each iteration and the corresponding complexity is denoted asCupd.In addition,n2LDPC codewords andk2/mRS codewords are required to decode for a product codeword.Assuming that the decoding complexity of an LDPC codeword is represented byCLDPC,the decoding complexity of a RS codeword is represented asCRS,the complexity of product decoding can be expressed as

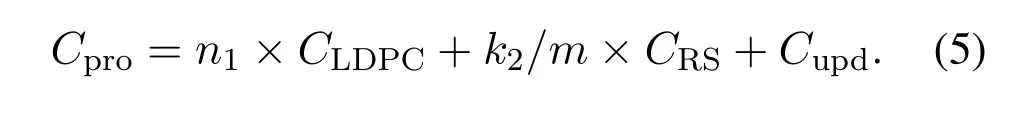
For decoding ofn1LDPC codeword,the computational complexity is shown in Table2,wherewrandwcdenote the row weight and column weight of parity check matrix of the LDPC code,NIterrepresents the number of iterations set by BP decoding.It can be clearly observed thatCupd＜＜n1×CLDPC,and the multiplication calculation of LDPC decoding is hundreds of times as much as that of the update procedure.Therefore,the complexity of product decoding can berewritten asn1×CLDPC+k2/m×CRS.

Table2.The complexity of LDPC decoding information update.

In summary,considering that the processing of the decoding priori information update is quite simple,the complexity can be neglected in the analysis.Most complexity increasing is due to the iterative decoding in the following iterations.In the new iteration round,only those codewords not satisfying the parity-check matrix need to perform the new round of decoding.The number of codewords which need to act is directly related to the code error rate.

When the iterative decoding of the product code works,the code error rate is quite low and the increased complexity is quite limited.It can be observed that in Figure5,for the product code is composed of LDPC(576,288)and RS(255,251)over GF(28),whenEb/N0is 2.0 dB,the error rate of LDPC code for frist iteration round is about 0.051 and thus at most only 5.1%LDPC codewords need to execute the LDPC decoding again.It is similar for the RS code.As SNR increases,the additional complexity added by iterations becomes much less.

In summary,due to the fact that LDPC codes show signifciant error correction performance and RS codes only need to eliminate the sparse residual errors,only a small number of codewords need to perform the new round of iterative decoding.Therefore,the proposed iterative decoding brings little additional computation complexity.

3.2.3 The Memory,Routing and the Computational Complexity Comparison

In this part,taking the regular LDPC code as an example,the complexity for LDPC(n2,k2)-RS(n1,k1)product code and LDPC (n2× n1,k2× k1) code is analyzed in three aspects.

Figure5.The number of average additional codewords required for decoding in the iteration rounds when Eb/N0 is 2.0 dB.

First,the computational complexity is compared.During the decoding process,the messages ofn2×n1variable nodes andk2× n1check nodes need to be updated for LDPC(n2,k2)-RS(n1,k1) product code.Different from the product code,the LDPC(n2×n1,k2×k1)code needs to update the messages ofn2×n1variable nodes andk2×(2n1-k1) check nodes.If the long LDPC codes and LDPC codes in product construction use the same degree distribution,the computation complexity is similar,though 2n1-k1＞n1.Meanwhile,the product codes need to perform RS decoding and bring additional complexity.

Second,the memory usage is analyzed.Assuming the quantization bit-width isqand the column weight of the check matrix for LDPC code isdv,the required storage bits for the extrinsic information of LDPC code is

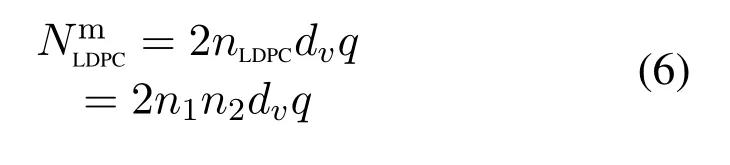
wherenLDPCis the code length of long LDPC code.For LDPC(n2,k2)-RS(n1,k1)product code,the storage bits can be expressed as

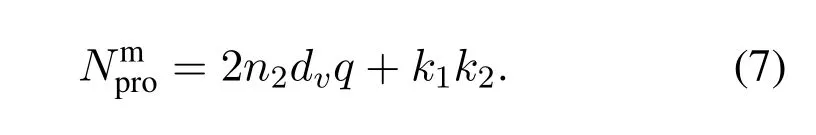
It can be observed that additional 2(n1-1)n2dvqk1k2bits need to be stored and processed.

Third,the routing complexity in implementation is analyzed.The total number of message wires required to connect the variable and check nodes is the same as the number of storage bits.It has been pointed out that the routing problem of LDPC codec using fully parallel architectures is quite a challenge[39].

Specifically,we take LDPC(576,288)-RS (255,251) product code and LDPC (576×255,288×251)code as an example for detailed comparison in the following.When the average column weight of LDPC code is about 3,the quantization bit-width is 6,and the RS code is defined over GF(256),the specific results are given below.The computational complexity of variable node for product code is same as LDPC code and the corresponding value is 146880×Cv,but the computational complexity of check node for product code is 73440×Ccwhile the computational complexity of check node for LDPC code is 74592×Cc,whereCvandCcare used to indicate the computation complexity of the variable node and check node update respectively.The memory or routing complexity of the product code is 93024 while the corresponding value for LDPC code is 5287680.

In summary,compared with the LDPC (n2× n1,k2× k1) code,the computational complexity of the LDPC(n2,k2)-RS(n1,k1) product code doesn't have obvious advantage.However,in terms of memory usage and the routing complexity,the product code has obvious advantages.Meanwhile,in terms of performance,the LDPC code exits the error floor even though very large code length is chosen and the product code doesn't have obvious error floor.Therefore,the proposed product codes are pragmatic schemes for high speed ultra-reliable communications.

IV.SIMULATION RESULTS AND ANALYSIS

In this section,we give simulation results to verify the proposed product code decoding algorithm.The simulations are performed under the AWGN channel with BPSK constellation.

4.1 Verification of Hybrid Error-Erasure-Correction Decoding

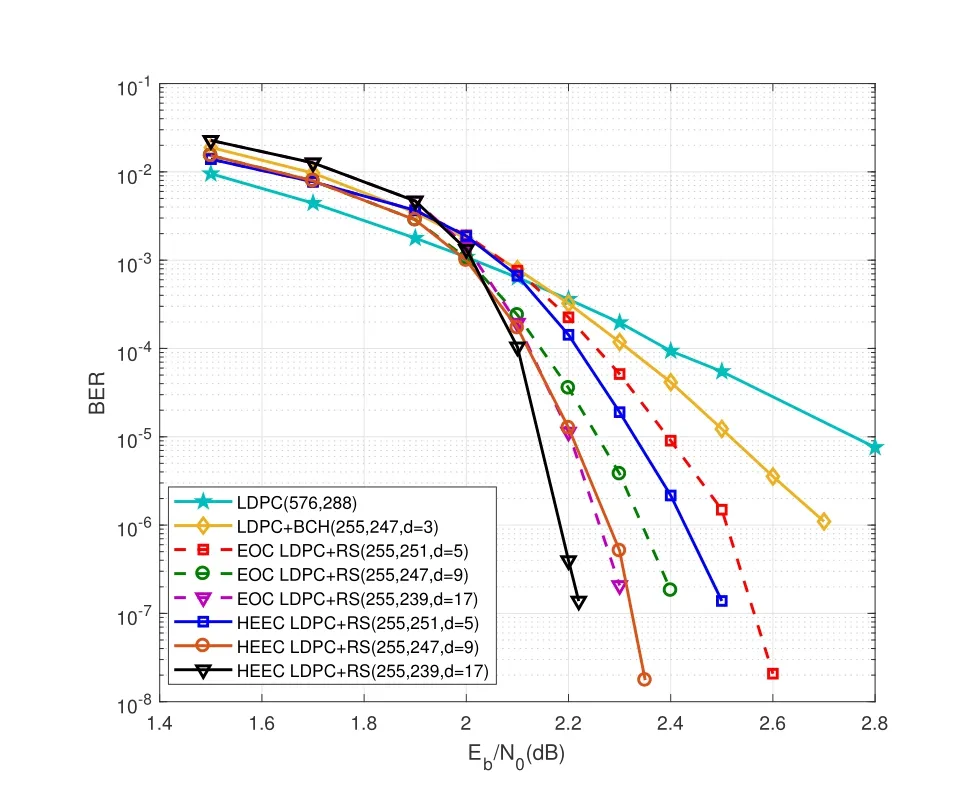
Figure6.Performance comparison of different decoding algorithms.

The performance comparison between the HEEC algorithm and the EOC algorithm is first presented.The results of different decoding algorithms combined with the product codes with different code rates,are shown in Figure6.The inner code is LDPC code with the code length of 576 bits and the code rate of 1/2,and the outer code is RS (255,251,5) over GF (28).The results show that when BER is 10−6,compared with the EOC algorithm,the performance of the proposed hybrid decoding scheme has the coding gain of 0.1 dB.Apart from this,it can be observed that LDPCRS product code with RS (255,247,9) has the coding gain of about 0.3 dB compared with LDPC-BCH(255,247,3)product code,when BER is 10−5.If the erasure-correction capability of outer codes increases,the performance gain is much more obvious.

Although the outer code with very high code rate is selected in this paper,the code rate loss still exists in the product code.WhenEb/N0is lower,the residual error after LDPC decoding is not within the error-erasure-correction capability of the RS/BCH code,thus the RS/BCH code cannot fully play its role.Therefore,the LDPC curve intersects with other curves at very low SNRs.

4.2 Verification of Performance Improvement with Iterative Decoding

In this part,performance of the proposed iterative decoding method for updating the priori information is examined.

First,the iterative performance comparison between the HEEC decoding algorithm proposed in this paper and the EOC decoding algorithm is shown in Figure7.It is clear that the performance of the proposed algorithm has a signifciant gain compared with the EOC decoding algorithm.Under the same number of iterations,the proposed method gains 0.1 dB compared with the EOC decoding,when BER is 10−7.Meanwhile,as the number of iterations increases,the performance of product code is gradually enhanced.When BER is 10−7,the performance with two iterations brings about 0.35 dB coding gain compared with the scheme without iteration.

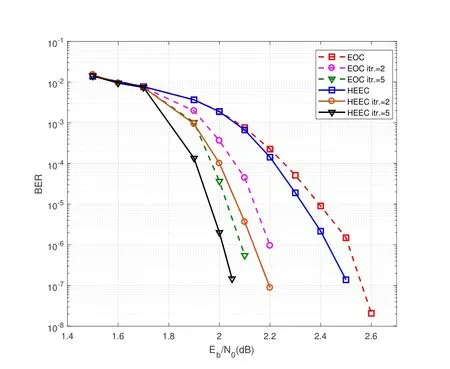
Figure7.Performance comparison of different decoding algorithms using LDPC-RS(255,251)product code.

4.3 Further Verification Using Other Code Parameters

Figure8.Iterative decoding performance of product code composed of LDPC (2304,1152) code and RS code with different code length and code rate.

In this subsection,the product codes using different LDPC codes are investigated.Simulation results of the product code using LDPC (2304,1152) and the series of RS codes are plotted in Figure8.When SNR is 1.7 dB,the BER of LDPC-RS product code with the hybrid error-erasure-correction decoding algorithm is reduced by three orders of magnitude compared with LDPC-BCH product code.In addition,when SNR is 1.5 dB,the BER is reduced by 3 to 4 orders of magnitude compared with the performance without iteration.From the simulations,we can confirm that the proposed product code and iterative decoding can be applicable to LDPC codes with different code lengths.Furthermore,in order to verify that the proposed iterative decoding is applicable to different types of LDPC codes,the typical quasi-cyclic LDPC code defined in the Chinese digital terrestrial multimedia broadcast(DTMB) standard with the code length of 7488 bits and the code rate of 0.4 is simulated [40].Figure9 illustrates that the LDPC-RS product code with the HEEC decoding algorithm has 0.1 dB coding gain at BER of 10−7compared with the LDPC-BCH product code.Meanwhile,LDPC-RS product code with the HEEC decoding algorithm brings additional coding gain of 0.04 dB compared with error-only-correction decoding algorithm.The overall performance of iterative decoding is improved by 0.12 dB compared with HEEC decoding without iteration at BER=10−7.In conclusion,the product codes using LDPC codes and RS codes can achieve ultra low BER when combined with erasure-correction enhanced iterative decoding.

Figure9.Iterative decoding performance of product code composed of LDPC(7488,3048)code and RS code.

V.CONCLUSION

In this paper,we construct product codes using LDPC codes and high rate RS codes to combat the error floor and to minimize the rate loss.Furthermore,the erasure-correction-enhanced iterative decoding algorithm is proposed to fully exploit the potential of erasure-correction capability of RS codes.Simulation results reveal that the proposed hybrid decoding algorithm surpasses the error-only-correction decoding algorithm by exploiting erasure-correction capability.Compared with LDPC-BCH product code,the proposed LDPC-RS product code shows obvious performance gain and the performance of product code can be further guaranteed using iteration.The advantages of the proposed schemes can be summarized as follows.Product construction can achieve low error rate,obtain proper parallel level and complexity.RS codes can help to obtain minimum rate loss of product construction due to their MDS property.Erasurecorrection-enhanced schemes help to exploit the error and erasure correction potential of product construction and it is also compatible with the erasure identification capacity due to the relatively large minimum distance of LDPC codes.

ACKNOWLEDGEMENT

This work was supported in part by National Natural Science Foundation of China (No.61671324)and the Director's Funding from Pilot National Laboratory for Marine Science and Technology (Qingdao)(QNLM201712).