A Game-Theoretic Perspective on Resource Management for Large-Scale UAV Communication Networks

Jiaxin Chen,Ping Chen,Qihui Wu,Yuhua Xu,Nan Qi,2,Tao Fang

1 Key Laboratory of Dynamic Cognitive System of Electromagnetic Spectrum Space,Ministry of Industry and Information Technology,College of Electronic and Information Engineering,Nanjing University of Aeronautics and Astronautics,Nanjing 211106,China

2 State Key Laboratory of Air Traffic Management System and Technology,Nanjing 210014,China

3 28th Research Institute of China Electronics Technology Group Corporation,Nanjing 210007,China

4 College of Communications Engineering,Army Engineering University of PLA,Nanjing 210007,China

Abstract:As a result of rapid development in electronics and communication technology,large-scale unmanned aerial vehicles (UAVs) are harnessed for various promising applications in a coordinated manner.Although it poses numerous advantages,resource management among various domains in large-scale UAV communication networks is the key challenge to be solved urgently.Specifically,due to the inherent requirements and future development trend,distributed resource management is suitable.In this article,we investigate the resource management problem for large-scale UAV communication networks from game-theoretic perspective which are exactly coincident with the distributed and autonomous manner.By exploring the inherent features,the distinctive challenges are discussed.Then,we explore several gametheoretic models that not only combat the challenges but also have broad application prospects.We provide the basics of each game-theoretic model and discuss the potential applications for resource management in large-scale UAV communication networks.Specifically,mean-field game,graphical game,Stackelberg game,coalition game and potential game are included.After that,we propose two innovative case studies to highlight the feasibility of such novel game-theoretic models.Finally,we give some future research directions to shed light on future opportunities and applications.

Keywords:large-scale UAV communication networks;resource management;game-theoretic model

I.INTRODUCTION

With rapid improvement in electronics and communication technology,unmanned aerial vehicles (UAVs)have numerous promising applications in military and civilian domains due to their versatility,high mobility,fast deployment and flexibility [1,2].For example,UAV has been applied for various tasks including target localization[3],surveillance and reconnaissance [4]as well as coverage [5].As depicted in Figure1,UAVs are capable of reconnaissance and target localization,traffic monitoring,improving users'data rate and traffic offloading opportunity in emergency situations where the ground cellular infrastructure is limited and temporary hotspot areas such as concerts and matches,independently or cooperatively.Low-altitude UAV is a cost-effective,fast and flexible deployment while the high-altitude UAV can provide wide coverage for long endurance [2].With the miniaturization and cost reduction of UAVs,largescale UAV swarm,consisting of dozens or hundreds of small UAVs,becomes possible and is expected to achieve high performance that go beyond the individual UAV.Specifically,coordination and collaboration of UAVs can decrease the acquisition and maintenance cost,improve the task performance,increase survivability and scalability.Deploying UAVs for wireless communication is regarded as one of the most important applications.For instance,UAVs can serve as flying base stations (BSs) to enhance capacity of cellular networks and maintain wireless coverage and connectivity without terrestrial BSs.Although applying large-scale UAV swarm poses several advantages,it comes with the novel and tough challenges in resource management such as spectrum allocation,power control,interference management and task allocation.It is noted that different from terrestrial communication networks,there is a need for a framework to dynamically manage various resources including energy domain,spectrum domain,power domain,space domain and so on.Specifically,distributed resource management is suitable for large-scale UAV communication networks due to the following reasons:

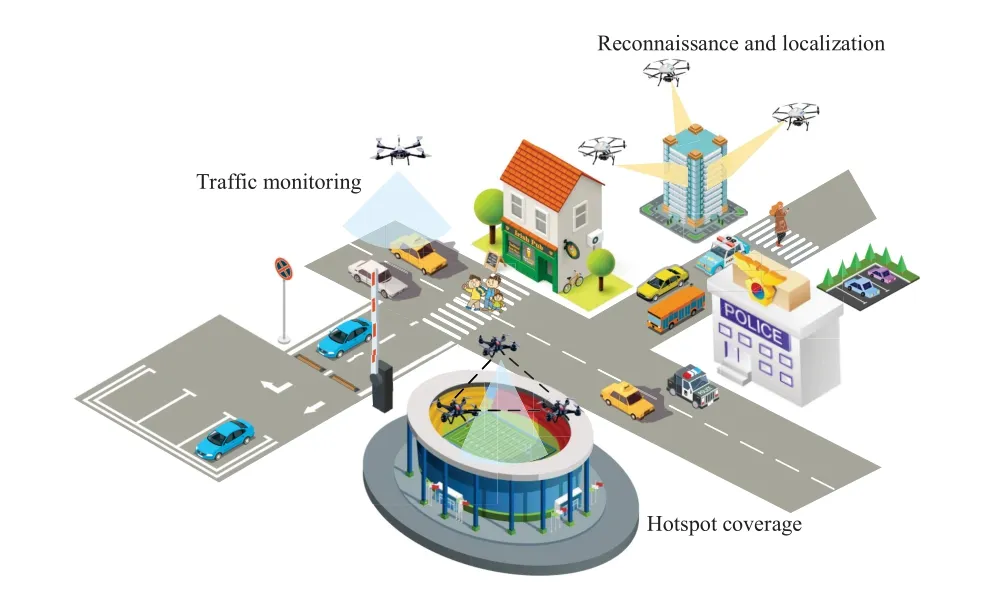
Figure1.The examples of UAV in numerous task scenarios.

·Distributed decision making will be a developing trend of multi-UAV networks in the future.UAVs are foreseen to have the ability to complete complex task to adapt dynamic and severe environments in order to ensure the highest level of task autonomy.

·The large-scale deployment of UAVs leads to intractable computational complexity when applying centralized framework.Moreover,various resources allocation aggravates the complexity since strategy space may grow explosively.

·Centralized resource management requires information exchange among whole network.It is difficult to obtain the information in terrestrial network,not to mention complex electromagnetic environment with high mobility feature.Although the information is available,the excessive overhead and delay cannot be neglected.

Game theory,a branch of applied mathematics,is a natural and powerful tool to analyze mutual interactions among multiple decision-makers.It was primarily applied to investigate the competition or cooperation behavior in economics [6].For over a decade,it has been verified that game theory can successfully address resource management in terrestrial wireless communication network such as cognitive small cells(CSCs)[7]and wireless Internet of Things(IoT)system[8].

In this article,following the distinctive features and challenges from essential attribute to external performance in large-scale UAV communication networks,we move forward to some game-theoretic models that not only combat the challenges but also have broad application prospects.However,the distinctive features of large-scale UAV communication networks make the game theory quite different from previous resource management in terrestrial networks as shown in Figure2.In particular,the differences include,but are not limited to:

·Variety of players:Due to the inherent task-driven essence,different types of players (e.g.,UAVs,terrestrial base stations and tasks) and their roles in communication task(e.g.,relays or aerial base stations) are involved in a game while we often assume that players are of the same type without roles in terrestrial communication networks.

·Multi-domains strategy space:In existing terrestrial communication networks,resource management are mainly implemented in spectrum and power domains.Due to three-dimensional (3D)deployment and limited energy supply,space domain and energy domain are involved which results in multi-domains strategy space.

·Diversity of interactions:There exists different kinds of communication links such as UAV-to-UAV(U2U),UAV-to-Satellite(U2S)and UAV-to-Ground (U2G) links.Hence,different channel characteristics may result in the diversity of interactions when implementing resource management.Moreover,dynamic mutual interactions caused by high mobility(e.g.,dynamic mutual interference due to topology change)is regarded as a supplement diversity.

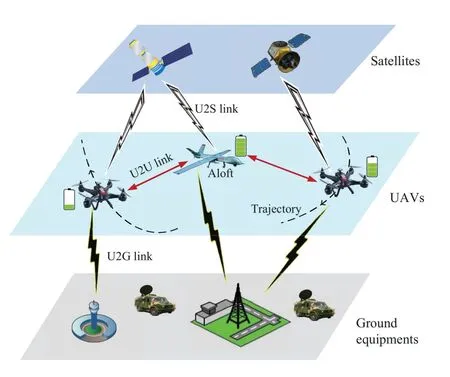
Figure2.An example of UAV communication network consisting of satellites,UAVs and ground equipments.

Therefore,it is imperative to find game-theoretic models of resource management which can fit the characteristics of large-scale UAV communication networks more appropriately.To this end,the objective of this article is to propose the game-theoretic models suitable for distributed resource management in largescale UAV communication networks.Although there exist numerous surveys which focus on different important issues in UAV communication networks ranging from use cases of UAVs[2,9]to channel modeling[10].However,a few surveys that review analytical resource management frameworks and solutions for large-scale UAV communication network have already been out.The authors in [11]summarized the existing game-theoretic solutions applied in UAV wireless communication and proposed mean field game(MFG)to solve massive UAVs scenarios.Nevertheless,this survey only focused on game-theoretic solutions in aspects of different optimization problems while lacked the exploration of the nature of different game models which implied why these games can address different intractable challenges in large-scale UAV communication networks.

The remainder of this paper is structured as follows.In Section II,we first outline the distinctive features and challenges in large-scale UAV communication networks.Some key challenges and requirements which should be taken into account when implementing distributed resource management are also discussed.In Section III,we thereby present some game models for large-scale UAV communication networks in a tutorial manner.Then,we propose two innovative case studies to motivate the readers and highlight the feasibility of such novel game-theoretic models in Section IV.Afterwards,some future research directions are given in Section V.Finally,Section VI concludes the article.

II.CHALLENGES IN RESOURCE MANAGEMENT FOR LARGE-SCALE UAV COMMUNICATION NETWORKS

In the following,we briefly outline the distinctive features from essential attribute to external performance in large-scale UAV communication networks.We then discuss key challenges when implementing resource management in such networks.

2.1 Three-dimensional Large-scale Deployment

As a result of flight in the air,deployment of UAVs is extended from two-dimensional (2D) space to 3D space.Hence,the resource management in spatial domain is expected to be considered since 3D deployment will affect interference intensity and demand requirements.Moreover,large-scale UAV swarm has become the wave of the future which has aggravated the resource scarcity which leads to high competition and network congestion.Consequently,resource management should be done while considering serious mutual interference among UAVs.

2.2 High Mobility

The widespread use of UAVs depends mainly on its high mobility.However,such great advantage makes efficient management of resource challenging.The network topology may change rapidly and dynamically which causes dynamic mutual interference and network connectivity.Meanwhile,the terrain environment (e.g.,building density) caused by high mobility is expected to change frequently.Hence,the wireless environment,such as channel quality,may change accordingly.The fast decision-making resource management method is needed when UAV's mobility is considered.

2.3 Limited Energy Supply

Besides the energy expenditure which is related to communication (e.g.,data transmission and signal processing),UAVs must consume considerable energy to maintain their flight states,i.e.,propulsion energy.The limited payload of UAVs constrains the onboard energy which may affect the performance of UAV since it needs to be recalled for recharging/refueling.Hence,under this limitation,resource management should be energy-efficient.

2.4 Task-driven Essence

The boom in UAVs is mainly caused by their superior performance in various tasks.Not only the UAV flight control but also the communication requirement follows the task-driven characteristic.That is,it follows top-down communication requirement where the communication between UAVs is to complete the task effectively[12].Obviously,different tasks have different requirements such as throughput requirement and delay requirement.Therefore,task-related resource management when considering task priorities,UAV trajectories,resource utilization demand requirements and priorities needs to be designed urgently.

2.5 Complex Electromagnetic Environment

Besides the mutual interference inside the UAV swarm which may cause complex electromagnetic environment,the existence of malicious jamming is more intractable.Once the links are jammed,the communications between UAVs will be interrupted.What's more,malicious jamming may lead to conditions ranging from unmanageable control to UAV crash.Robust resource allocation in power domain,spectrum domain as well as spatial domain should be designed with anti-jamming ability.

III.GAME-THEORETIC MODELS FOR RESOURCE MANAGEMENT

Game theory,a branch of applied mathematics,is a natural and powerful tool to analyze mutual interactions among multiple decision-makers [13].Generally,the three major elements of a game are players,strategy set and utility functions.The key idea of game theory is that the players choose their actions which can maximize their utilities at the level of themselves in a distributed manner.We first give the brief introduction of the game model from two aspects,noncooperative game and cooperative game.

·Non-cooperative game:It is one of the most elemental branches of game theory which studies the strategies among players where each player only maximizes its utility by selecting best action independently and rationally.Formally,the non-cooperative game is often denoted as strategic-form representation,i.e.,F={N,{An}n∈N,{un}n∈N},where

N={1,2,···,N}is the player set,Anandunare the strategy set and utility function of playernrespectively.In non-cooperative game,Nash equilibrium (NE) is the crucial solution concept.Obtaining a NE state is often the ultimate objective in the game.We give the definition of NE as follows:

Definition 1(Nash equilibrium).A strategy profile a∗=(a∗1,a∗2,···,a∗N)is a pure-strategy NE if and only if no player can improve its individual utility by deviating its strategy unilaterally while other players keep theirs unchanged,i.e.,

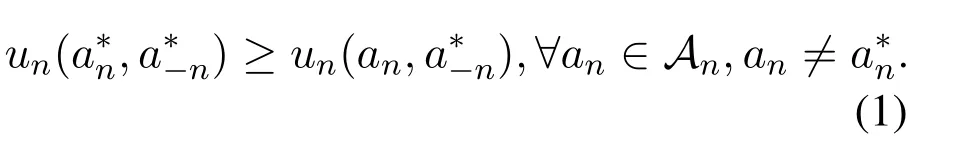
·Cooperative game:Unlike non-cooperative game where each player only considers its own utility,cooperative game focuses on the competition between groups of players,i.e.,coalitions.In cooperative game structure,the players are grouped in accordance with an enforceable agreement and then select their actions.The main consideration always focuses on how to form the coalition and how to fairly allocate the payoff among players in the same coalition to stabilize the coalition.

In methodology,there exist numerous game-theoretic models for resource management in wireless communication networks.However,most solutions suffered from some shortcomings and did not consider the features and challenges for resource management in large-scale UAV communication networks.Therefore,in the following,we explore five kinds of novel game-theoretic models for distributed resource management to fit the characteristics of future large-scale UAV communication networks more appropriately.

3.1 Mean-field Game

3.1.1 The Introduction of Mean-field Game

Mean field game (MFG) theory,a special form of a differential game,is a promising and powerful tool to model and analyze dynamics of large number of interacting rational agents in large-scale communication network.Generally,in MFG,each player hasa set of actions,a state space,control policyandcost function.The state space can be single-dimensional or multi-dimensional,such as the remaining energy or the locations of UAVs.The control policy maps every state into an action in order to minimize the cost function.The introduction of mean filed can replace a large number of players'individual interactions into the average effect of the collective behavior in the game.The mean field,the most important concept in MFG,captures the relation between all interactions to an arbitrary player and an average interaction.For example,the generic player can make optimal decision only considering the mean field value,instead of the strategies of other players.Mathematically,to characterize the mean filed,we give the following definition:

Definition 2(Mean field).Given the state space of player n at time t sn(t),the mean field m(t,s)is:

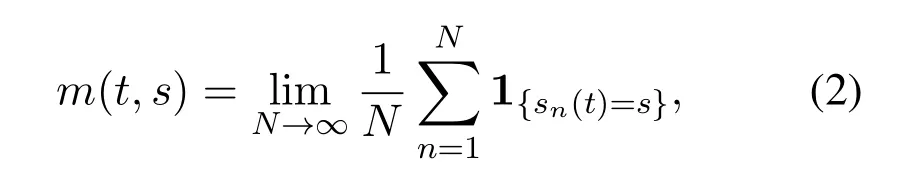
where1denotes an indicator function.

When the condition is true,the function returns to 1,otherwise,it returns to 0.Actually,the mean field can be regarded as the statistical density distribution of the network state dynamics of mass players.

MFG is a coupled system consists of a Fokker-Planck-Kolmogorov (FPK) equation for a mean field function and a Hamilton-Jacobi-Bellman(HJB)equation for a value function[11].FPK and HJB are partial differential equations.The former one,also called forward equation,can govern and measure the dynamics of mean field function in accordance with the strategies of players.The later one,backward equation,models the interaction of the player and mean field and governs the computation of the optimal path for each player.

The mean field equilibrium(MFE)indicates the stable combination of the control policy and mean field at any time and state [14].It can be achieved by solving FPK and HJB equations simultaneously.In existing studies,finite difference technique is an efficient method which is widely used to obtain MFE[15].Also,finding the closed-form solution is a common method[16].However,it is still an open research to find the general technique which can solve the FPK and HJB equations.

3.1.2 The Application of MFG in Resource Management

MFG has been widely used in resource allocation in ultra-dense networks and hyperdense heterogeneous networks due to its superiority of describing the behavior of large number of players solely with two equations[14,15].Therefore,interference management involving power control and channel allocation in largescale networks can be solved quiet well.

More importantly,since the stochastic nature of the MFG,it coincides with the high dynamic nature which is specifically embodied in location dynamics,channel dynamics and energy dynamics in UAV communication networks.For instance,the authors in[17]investigated the velocity control problem for massive UAVs which are deployed to build the connections in emergency scenarios.Each UAV aimed to minimize its energy consumption per unit downlink rate.The location and velocity could be regarded as the state and control.The velocity of an individual UAV was obtained by solving HJB function while the resultant UAV movements,i.e.,changes of locations,were determined by FPK function.Note that due to the time-varying continuous control is not realistic such as power control,the discrete-time MFG has raised lots of concerns.In discrete-time MFG,the mean field term is characterized by proposing the population state average(PSA)which can describe the dynamic equation.In [16],the authors investigated coverage problem where each UAV adjusts their location coordinate aiming to minimize the energy consumption containing the average distribution of all UAVs.In [18],the authors studied the probability of successful transmission under the consideration of two-dimensional states(emission energy state and distance state)optimized by two controls(transmission power and speed of UAVs).

Therefore,MFG can be perfectly applied to solve interference management,power control and velocity control problems in large-scale UAV communication networks.Energy-aware resource management under large-scale deployment and high mobility are typical potential applications of MFGs in the context of largescale UAV communication networks.

3.2 Graphical Game

3.2.1 The Introduction of Graphical Game

Graphical game is a novel and advanced game which is characterized by:the players are regarded as nodes and the mutual impacts are denoted by edge in a graph.The utility function of each player only depends on itself and its neighbors rather than all players in the game.Compared to conventional game,it introduces an undirected graph G=(V,E)whereVis the vertex set,as the player set andEis the edge set which represents the mutual impacts between two vertexes.From the perspective of communication,the setting of a graphical game can naturally capture the underlying game structure in many realistic environments[19].This novel game model has been studied extensively in the literature in opportunistic spectrum access(OSA)systems[20].In the following,we summarize five kind of graph models and their applications with the combination of game theory.The illustration of the graph models is shown in Figure3.

Local interaction game model:Due to the low transmit power and fading in wireless communication system,the strong interference only occurs in a limited particular range.This feature can provide a promising spectrum reuse opportunity OSA systems.The authors in [21]proposed local interaction graph model,where the communication nodes are classified into two categories:neighbors and non-neighbors.The vertexes located in a limited range causing severe impact are defined as neighbors while others are nonneighbors.As illustrated in Figure3(a),only neighbors of vertex 1,i.e.,vertex 2 and 3 may cause impact on vertex 1.In[21],the authors studied local interaction game to solve OSA in cognitive radio networks in order to maximize network throughput and minimize network collision.

Edge-weighted graph model:Although local interaction graphical game is a powerful way to perform spectrum spatial reuse,sometimes,it ignores the diversity in mutual impacts due to the uneven user distribution [22]in practical wireless communication networks.For example,interference among network access points (NAPs) can be different.Motivated by the above limitation,the authors in [23]proposed two kind of edge-weighted graph models to capture actual degree of mutual impact as shown in Figure3(b) and Figure3(c).In this model,the introduction of edge weights and directions can reflect the differences between mutual impacts.When combining edge-weighted graph model and game theory,the authors in[23]formulated weighted graphical game to solve spectrum access self-organization problem in an effective way.

Vertex-weighted graph model:Different from edge-weighted graph model which considers the diversity in edges,the diversity in vertexes is also a challenging problem.For example,small cells may have different loads,i.e.,the number of mobile users in small cells may be different.Hence,different number of channels is required for different small cells.To overcome this limitation,the authors proposed vertexweighted graph model[24].The illustration is shown in Figure3(d)where the weights of vertex 1,2 and 3 are 3,2 and 4 respectively.Mapping the vertex weight to small cell networks,it means that the small cell 1,2 and 3 need 3,2 and 4 channels respectively to avoid intracell interference.In [24],the vertex-weighted graphical game was formulated taking the features of different cell loads and local interference into consideration in OSA for small cell networks.

Generalized graph model:In the abovementioned graphs,it is supposed that the communication node is only affected by its neighbors.However,in reality,it is not precise since not only the strong impact but also the cumulative weak impact caused by the communication nodes out of neighborhood may threaten the communication quality.The generalized graph model,which is first proposed in[25],is a simple and efficient structure to depict accumulative impacts in dense wireless communication networks.As depicted in Figure3(e),the communication nodes are classified into various distance-dependent neighborhoods.Longer distance yields weaker impacts.Thus,the weight function of each distance must be an inverse proportional function about distance.Introducing the generalized graph model into game theory,the authors in [25]applied generalized graphical game to study Almost Blank Subframe (ABS)-slot access optimization problem from interference mitigation standpoint.

Figure3.An illustration of five kind of graph models.

Hypergraph model:In future ultra-dense largescale communication networks,the deployment of numerous low-power communication nodes is the trend.When several low-power nodes transmit concurrently,the cumulative impact may affect transmission performance.The binary graphs,e.g.,local interaction graph and weighted graph,ignore the accumulated impacts due to that each edge contains only two vertexes.Hypergraph is the extension and expansion of binary graph which is characterized by:one hyperedge can join any number of vertexes [26].As shown in Figure3(f),the dash lines represent the strong relationship while the closed curve indicate the cumulative weak impacts.For instance,for hyperedge 4,vertex 8,9 and 10 can bring strong impact to vertex 1 when they transmission concurrently.In[26],the authors investigated the mutual interference in D2D communications using hypergraph game.Moreover,the combination of generalized graph and hypergraph was investigated in[27].

In graphical game,NE is the most commonly used representation of equilibrium solution.Under the framework of NE,numerous algorithms,such as regret minimization [28],spatial adaptive play (SAP) [21],can be applied to find the NE.Moreover,another equilibrium in graphical game is called evolutionary stable strategy(ESS),which is the solution concept of evolutionary games[29].Local exponential learning algorithm proposed in [29]can be applied to converge to ESS.

3.2.2 The Application of Graphical Game in Resource Management

When graphical game comes to addressing the resource management for large-scale UAV communication network,the most important aspect is the ability to model the interaction of a large network with graph model.One the one hand,the mutual interference can be modeled as the edge.In [30],we investigated the demand-aware resource management of UAV networks considering channel-slot allocation.We formulated the demand-aware interference level among UAV clusters using vertex-weighted graphical game.When the distance among UAV clusters is less than a threshold,interference may occur between them,i.e.,there exists an edge connecting two nodes.In addition,rapid topology change of UAV communication network due to its high mobility can also be characterized by modifying static graph into dynamic graph through introducing time variable in our previous work[31].

Another significant reason for applying graphical game model to UAV communication network is its topology-related feature.In order to perform the task efficiently,formation maintenance of multiple UAVs is needed.That is,UAVs should maintain the geometric configuration accurately between each other.To achieve that,neighbor-to-neighbor information exchange is needed which only relies on itself and its neighbors[32].This feature coincides with the definition of graphical game.

Therefore,graphical game is a good candidate to develop channel allocation,power control,topologyrelated resource allocation problems in large-scale UAV communication networks.Besides,compared to MFGs,graphical game provides another promising solution under high dynamic feature and large-scale deployment features.

3.3 Stackelberg Game

3.3.1 The Introduction of Stackelberg Game

In two previously game models,the players are considered the same which have no hierarchy.Based on this assumption,the network structure can be regarded completely distributed.Different from them,Stackelberg game is a suitable and promising framework to capture the hierarchical feature and model the hierarchical interaction among players.The Stackelberg model was first put forward in economics in which the leader firm decides its production moves first and then the follower firms decide their own productions according to the leader firm subsequently.Nowadays,it is widely extended to various fields.The general setting of Stackelberg game can be denoted as:the leader player takes an action first and then the followers take their actions sequentially.Mathematically,let 0 denote the index of leader andNf={1,2,···,N}represent the followers' set.Thus,the set of players isN=Nf ∪{0}.Formally,Stackelberg game model can be denoted asF1={N,{A0},{An}n∈Nf,{u0},{un}n∈Nf},where{A0}and{An}n∈Nfare the strategy space of leader and followers,respectively.In addition,{u0}and{un}n∈Nfare utility functions of leader and followers.In normal non-cooperative game,NE is a strategy profile such that if the opponents' strategies remain unchanged,no player may move away from its current strategy.That is,no player can improve its individual utility by deviating its strategy unilaterally while other players keep theirs unaltered[13].In Stackelberg game,NE can be extended to Stackelberg equilibrium(SE)from which neither the leader nor the followers can achieve higher utilities by deviating unilaterally.Thus,the definition is given as follows.

Definition 3(Stackelberg equilibrium [33]).The strategy profile(a∗0,a∗f)is called SE if a∗0maximizes the leader's utility anda∗f=(a∗1,,···,a∗N)is the best response of followers' subgame.Mathematically,the following conditions hold:

response strategies except for follower n.

It is not hard to find that the SE is basically composed of an optimal policy for the leader with respect to a Nash equilibrium of the followers.

A promising method [34]for achieving the desirable SE is to divide the optimization process into rounds.First,leader selects its action at the beginning of each round.Then,according to the leader's action,the followers' subgame will converge to the equilibrium.Finally,both the followers'subgame and leader's subgame will converge to equilibrium which is the SE of the game.For the continuous problem,convex optimization techniques,e.g.,Karush-Kuhn-Tucker (KKT) conditions,can be applied to obtain the SE solution.However,the convex optimization is powerless for the discrete problem.Thus,learning algorithms,such as reinforcement learning,stochastic learning automata,can solve the intractable problem[33].

3.3.2 The Application of Stackelberg Game in Resource Management

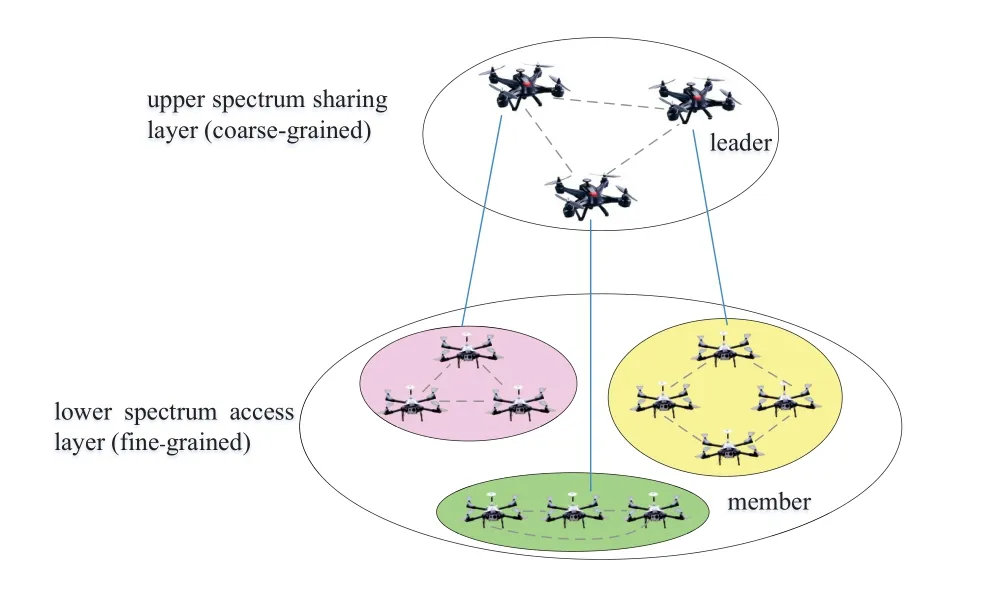
Figure4.An illustration of hierarchical and multi-granular UAV communication network architecture.

Stackelberg game models are regarded as one of the most promising tools for resource management in large-scale UAV communication networks.Most studies modeling the UAV communication network is flat[35]where UAVs do not have structural difference.However,due to the task essence feature,UAVs may form a coalition to complete specific tasks which results in coalition-based communication architecture,where the UAVs are divided into different coalitions consisting of coalition leaders and members.Hence,the network architecture is hierarchical and multigranular in essence.In the upper layer,the coarsegrained spectrum allocation among coalitions considering their heterogeneous communication demand can be investigated to reduce the inter-coalition interference while the lower layer studies the fine-grained task information fusion to mitigate the intra-coalition collision as depicted in Figure4.Specifically,the coalition leader is responsible for coordinating both the inter-coalition and intra-coalition communication.Such framework can accelerate the decision-making speed.To our best knowledge,the studies of hierarchical structure in UAV communication networks using Stackelberg games has not been reported yet.We believe that the hierarchical resource management is promising in future large-scale UAV communication networks.On the other hand,the existence of malicious smart jammers makes the electromagnetic environment more complex,which leads to link outage and fluctuation.Therefore,anti-jamming in power domain,spectrum domain as well as spatial domain are of great importance.As the users should detect the jammers' actions,or the jammers can learn users'actions,the hierarchical behaviors between users and jammers and the order of actions occur.Stackelberg game has been studied in UAV communication networks from single-user single-jammer[36]to multi-user single-jammer [37].In [37],the authors considered the malicious jammer as well as the co-channel interference among UAVs by formulating a Bayesian Stackelberg game.The sub-gradient based Bayesian Stackelberg iterative algorithm was proposed to achieve the SE.However,this research field is less explored and the existing research mainly focused on two-layer structure.In [38],the Stackelberg game was extended into three-layer when considering relay-assisted system where the relay users are acted as vice-leaders.This framework may be used in UAV-assisted relay system [39].Hence,Stackelberg game models is a suitable and promising framework for sequential decision-making of anti-jamming defence in UAV communication networks.Stackelberg game can find a much wider range of applications including power control,channel allocation and joint user scheduling.Thus,jamming-aware resource allocation is the potential application in large-scale UAV communication network.Moreover,it is noted that deep reinforcement learning is a popular method to solve anti-jamming communication problem without the information of jamming patterns and parameters[40].We believe that the combination of the game theory and deep reinforcement learning is a promising and potential way in the future.

3.4 Coalition Game

3.4.1 The Introduction of Coalition Game

Coalition game theory,a kind of cooperative game,studies the behavior of players when they cooperate.In this structure,the players are willing to seek to form cooperative groups,i.e.,coalitions,before selecting their actions.The formation of coalitions is ubiquitous in human society as well as large-scale UAV communication networks.For instance,company alliance will bring greater benefits to each other while UAVs may form coalitions based on the correlative task to improve their task performance.A comprehensive tutorial of coalition game theory oriented towards communication network can be found in[41].Coalition games cover a broad range of communication networks,such as spectrum sensing in cognitive radio network[42],popular content distribution in vehicular ad-hoc network(VANET)[43],resource allocation in heterogeneous cellular networks [44].In task-driven UAV communication networks,UAVs may form coalitions based on the correlative task.The partition of the whole UAV network and the selection of the coalition leader reflect the process of coalition formation.Also,the communication rules and the UAV formation are usually determined.Thus,we focus on coalition formation game (CFG) while omit canonical coalitional games,and coalitional graph games in this article.The coalitionSis a set of players who cooperate with each other such thatS ⊆NwhereNis the set of UAVs.In usual models of CFG,the coalition structure consists of disjoint,non-overlapping coalitions.That is,a coalition structureCO={S1,···,SK}satisfies the condition that∀n/=k,Sn∩Sk=∅and∪Kk=1Sk=N.Under this framework,stability analysis is an important part in CFG.Usually,Nash-stable and individually stable are the two stability concepts in CFG.

Figure5.An illustration of disjoint coalitions and overlapping coalitions in multi-UAV communication networks.

Definition 4(Nash-stable).A coalition partition is Nash-stable if no player can benefit from moving from his current coalition to another coalition.

Definition 5(Individually stable).A coalition partition is individually stable if no player can benefit from moving from his current coalition to another coalition while not hurting the benefits of the members of this coalition.

In CFG,preference order is a significant concept which is used to compare the preference of an arbitrary player over different coalitions.Different preference orders may affect the stability of CFG.Therefore,it is important to design preference orders not only fit for the proposed CFG but also ensure the convergence of stable coalition partition.Also,the merge and split rule is widely applied to obtain the stable coalition partition in CFGs [45].However,sometimes the appropriate coalition structure and its stabilization is hard to investigate.The potential game which is given in the following will be a powerful technique to prove the existence of stable solutions.

3.4.2 The Application of Coalition Game in Resource Management

On the one hand,spectrum allocation is a possible application of CFGs in UAV communication networks.First,UAVs who generate strong interference to each other may form a coalition.Then,the UAVs in the same coalition adjust their locations and select orthogonal channels to eliminate strong mutual interference[46].Therefore,interference management considering spectrum allocation is the potential application scenario.

Also,CFGs can be used in task allocation of UAVs,where UAVs are intended to form disjoint coalitions considering both tasks and resources.For instance,in[47],W.Saadet.alinvestigated the hedonic CFG for UAV-aided wireless networks where UAVs and tasks are intended to form disjoint coalitions considering the effective throughput as well as the delay.The subsequent extended version [48]proposed hedonic coalition formation algorithm to adapt the topology to environmental changes.However,due to the complexity or the association of tasks,an UAV may be involved in different tasks[49]as shown in Figure5.This feature has direct consequence:the coalition member is overlapping between different coalitions.This leads to overlapping coalition formation (OCF) game.The UAVs equipped with powerful devices which can utilize multiple resources may make it possible.For example,multiple-antenna user can devote its antennas to different coalitions.A preliminary case utilizing OCF game framework in UAV communication networks can be found in[50].The authors investigated the data transmission and resource allocation problem through coalitional graph game and OCF game respectively.Deciding the task allocation,demand-aware resource allocation and cooperative communication could be possibly modeled as CFGs in UAV communication networks.To summarize,CFG is very appropriate for task-related resource allocation.

3.5 Potential Game

3.5.1 The Introduction of Potential Game

In the above game models,obtaining the equilibrium is quiet challenging.For instance,the mean field equilibrium is achieved by solving FPK and HJB functions.However,there exists no general technique to solve them simultaneously.Potential game is a kind of non-cooperative game which has attractive properties concerning the existence and attainability of NE[13].Specifically,the straightforward application of potential games is that it can lead to a NE solution.Although it poses such attractive properties,how to formulate a problem as a potential game is the key challenge.The common thread is to find the potential function which maps the strategy space to the space of real number.Moreover,the potential function guarantees the utility of arbitrary player is aligned with the global objective.Nowadays,potential games are beginning to emerge as a valuable paradigm for wireless communication network varying from resource allocation to coalition formation.Especially,exact potential games(EPGs)have gained the most attention and practical applications.First,we give the definition of the exact potential game.

Definition 6(Exact Potential Game).A game is an EPG if and only if a potential function φ:A1⊗···⊗AN →Rexists such that for ∀n ∈N:

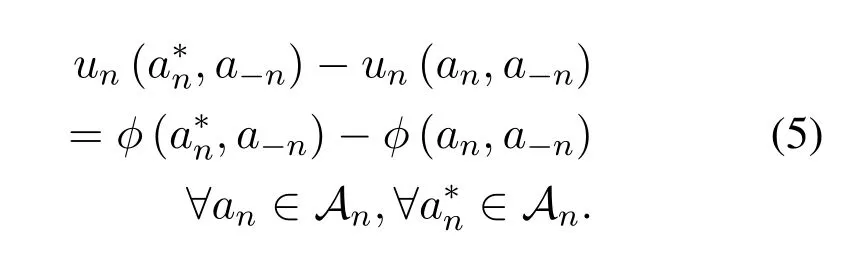
That is the change in the utility function due to the unilateral deviation of a single player is exactly the same amount of change in the potential function.To ensure that a game is an EPG,the following features are given:

·Self-motivated feature:the utility function of an arbitrary player solely depends on its own strategy.

·Bilateral symmetric interaction(BSI)feature:the utility function is only affected by the pairwise interaction between playernandiand does not depend on the rest of players.

·Local altruistic feature:the player considers its utility together with its neighbors'utilities during decision-making.This idea is motivated by local cooperation in biological evolution which was first introduced in [21]to improve the efficiency games since this model breaks through the restriction of traditional game model that players always act selfishly.

·Marginal contribution rule:this rule,also called wonderful life utility (WLU),is used to measure the contribution of a particular action of a player to the global utility,i.e.,the potential function.

In EFG,NE can be reached with certain learning algorithms.Best response and better reply are the two most commonly algorithms which can determine the player's strategy [13].Moreover,SAP,fictitious play can also be used to search the NE for potential game[6].However,these algorithms are coupled,i.e.,they need to know the actions or utilities of other players.To overcome the constraint,the authors proposed stochastic learning automata[51]and log-linear learning algorithm[52]which are more feasible in wireless communication systems.

3.5.2 The Application of Potential Game in Resource Management

In UAV communication networks,severe interference is the major challenge for communication system especially the existence of line-of-sight propagation characteristics.The BSI feature is suitable for modeling the mutual interference between UAVs[30,31].Although game theory is used to analyze mutual interactions between players,some factors in UAV communication networks are self-motivated.For example,energy consumption caused by wireless transmission as well as the mechanical movements or hover is only dependent on itself.A classic example can be found in [30].The mutual interference was modeled according to BSI feature while the energy saving due to status switching of transceiver was modeled by self-motivated feature.Such game formulation can directly lead to an EPG.Hence,potential game is suitable for both the energy-aware and interference-aware resource allocation in UAV communication networks.

Cooperation between UAVs is also a hot issue in large-scale UAV communication networks.Under such framework,local altruistic feature and marginal contribution rule play a significant role in potential game formulation.On the one hand,multi-UAV coverage is one of the main applications of UAV.The authors in [53]investigated the energy-efficient multi-UAV coverage problem where they considered the coverage utility based on the general UAV and its neighbors' detection range.The problem was formulated as a local altruistic game which aims at maximizing the whole coverage utility.On the other hand,marginal contribution rule has been gradually concerned in the field of multi-UAV network [54,55].Both the content-aware resource allocation as well as cooperative coverage can be solved through marginal contribution.Therefore,content-aware resource allocation and cooperative coverage resource allocation are among the potential applications of potential game in large-scale UAV communication networks.

In Table1,we summarize and compare the existing game-theoretic models in UAV communication networks.Also,in Table2,we highlight the main features of discussed game models in terms of challenges they can address and potential applications in largescale UAV communication networks.We can see the strong motivation to use game-theoretic approach for resource management.Although we can hardly find a specific game model to solve all the intractable challenges,they can be adapted to solve different needs for specific problem.

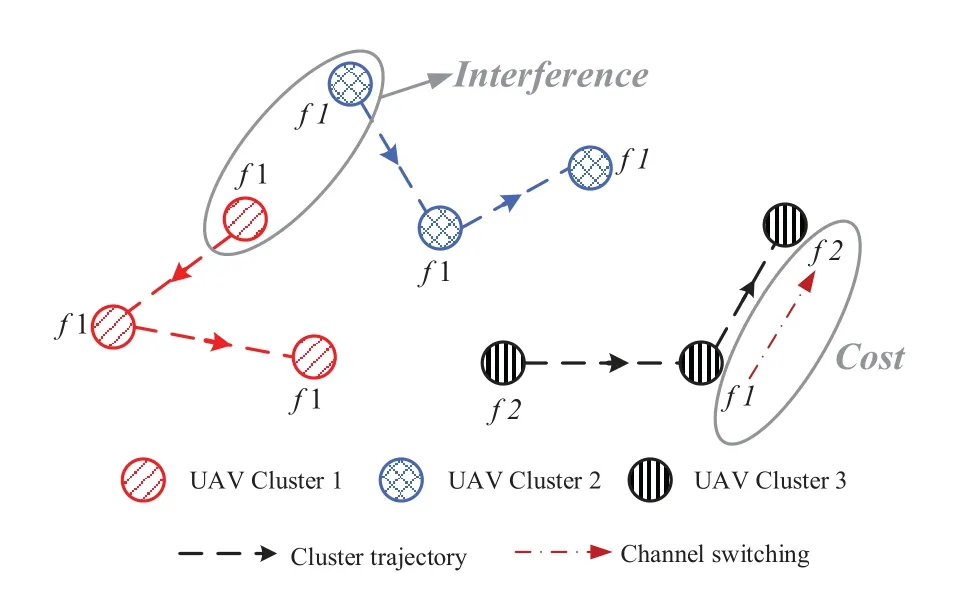
Figure6.An example of dynamic interference graph.

IV.CASE STUDIES

In this section,we present two innovative case studies to motivate the readers and highlight the feasibility of such novel game-theoretic models.

Figure7.The schematic of proposed algorithm in dataassisted multistage channel access game.

4.1 Interference-aware Online Channel Selection Game

Most existing channel selection game approaches assumed that the UAV topology is static.However,scenarios with rapid topology change due to its high mobility are more practical in UAV communication networks.In [31],we studied interference-aware online channel selection in Flying Ad-Hoc Network(FANET)when considering time-varying locations of UAV clusters and channel switching cost.A mul-ticluster FANET is considered in the system model,in which multiple clusters with different trajectories are included.Considering local interference feature,a data-assisted multistage channel access game is proposed with the aid of local interaction game model in graphical game.In addition,since the high mobility of UAVs,we modify the static interference graph into dynamic interference graph through introducing time variable.Due to the mobility and local interference,the clusters need to switch channels to adjust current environment.For better understanding,an example is shown in Figure6.Consequently,the utility function is designed as the weighted interference considering channel switching cost.Based on the BSI and selfmotivated feature in potential game,the NE solution is derived.As each cluster wants to minimize the interference and cost,we propose an interference-aware online channel preserving based concurrent best response algorithm to obtain the NE under the consideration of actual flight conditions.The schematic of the proposed algorithm is depicted in Figure7.

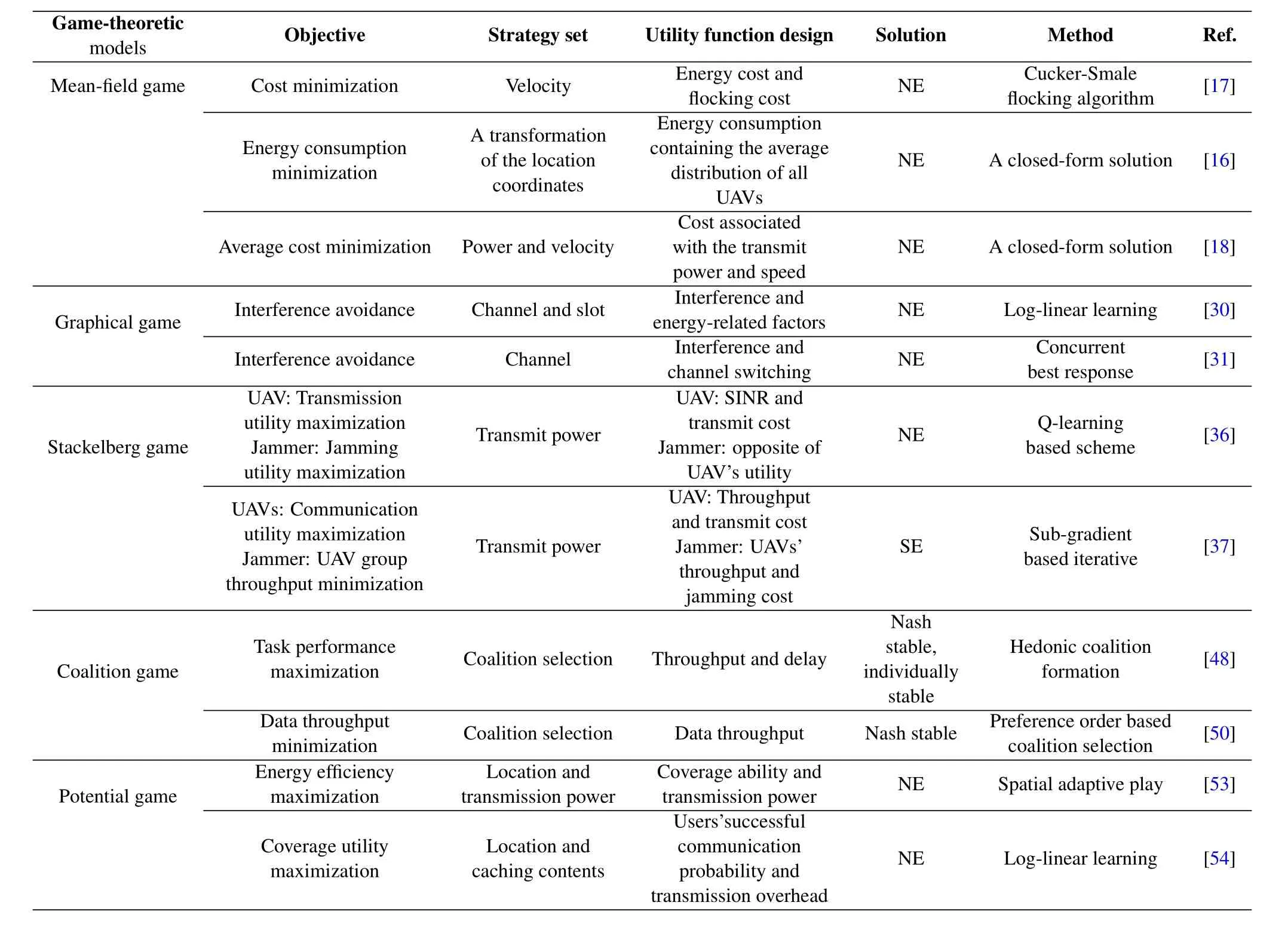
Table1.Summary of existing game-theoretic models in UAV communication networks.

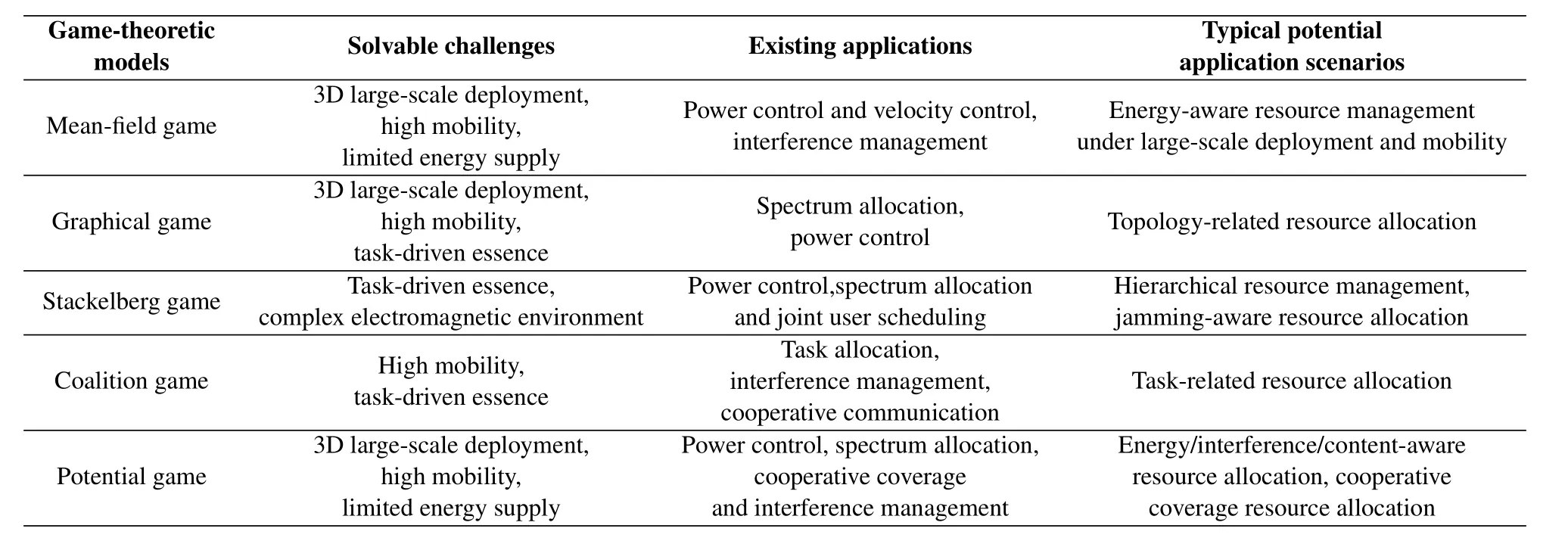
Table2.Summary of solvable challenges,existing applications and typical potential applications of large-scale UAV communication networks for each game-theoretic model.

In Figure8,we show the FANET aggregate utility and throughput for different solutions,i.e.,best NE,worst NE and random selection.It is noted that best NE and worst NE are regarded as the upper and lower bounds of the formulated game.It can be seen that the network utility and throughput obtained from the proposed algorithm are very close to the optimal value and significantly superior to the random selection method.In addition,increasing the number of channels results in an increase of the network utility and throughput.

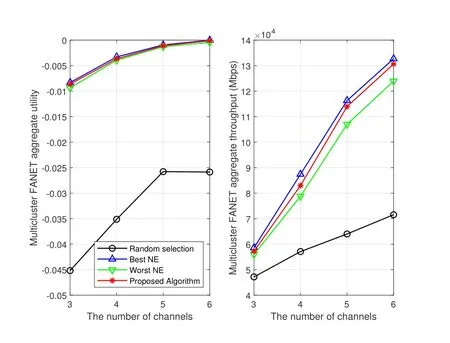
Figure8.The performance comparison of different solutions.

4.2 Joint Task and Spectrum Allocation Game

In this subsection,we investigate the joint task and spectrum allocation problem in heterogeneous UAVs communication networks where coalition game and potential game are applied.On the one hand,coalition structure is an effective networking architecture for task execution in large-scale UAV communication network.Therefore,appropriate task assignment may increase the task performance.On the other hand,resource allocation is also a key factor which can affect the intra-coalition communication.These two optimization problems are coupled which will affect the task performance simultaneously.In [56],we study the cooperative reconnaissance and spectrum access problem where UAVs form coalitions to perform reconnaissance tasks cooperatively.Each UAV first executes the task independently,and then transmits its reconnaissance information to its coalition head using the allocated bandwidth.Finally,the coalition head fuses the information received from the members and generate the final reconnaissance result.Coalition formation game is formulated to jointly optimize task selection and bandwidth allocation.The value function of each coalition is defined as the difference between task revenue and cost.Specifically,task revenue is determined by the task execution probability and task value while the task cost represents the hover energy and task risk.We then propose coalition expected altruistic order which aims at maximizing coalitions'utility.The existence of stable coalition partition is guaranteed with the help of EPG.

In Figure9 and Figure10,we evaluate the performance of the proposed scheme and preference order.First,we compare the performance under different orders as the task execution probability increases in Figure9.It is seen that the network utility increases as the probability increase.This is because higher probability yields higher task revenue.We can find that the proposed coalition expected altruistic order is superior to traditional orders,i.e.,selfish order and Pareto order.Also,the proposed joint optimization scheme can achieve higher utility when compared with the nonjoint optimization scheme which validate the effectiveness of the proposed scheme.In Figure10,we assess the total utilities of UAVs when increasing the number of UAVs.It is noted that the utility first increases to the maximum point and then decrease as the number of UAVs increase.That is,there exists a best number of UAVs when the number of tasks is fixed.The reason is that,the advantage of cooperation dominates the utility when UAV number is small while the cost of cooperation becomes higher than the revenue as the UAV number becomes larger.

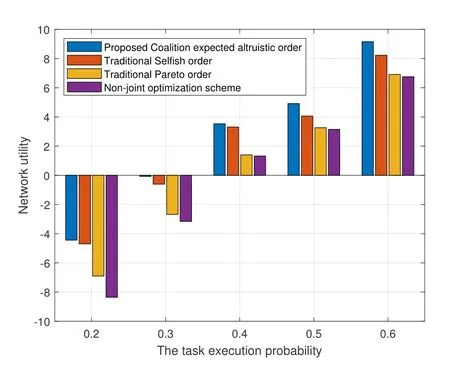
Figure9.The comparison results when varying task execution probability.

V.FUTURE RESEARCH DIRECTION

Although the aforementioned novel game-theoretic models can efficiently solve resource management in a distributed way,there still exists several potential open research problems.In the following,in order to shed light on future research opportunities,we list some future research directions.

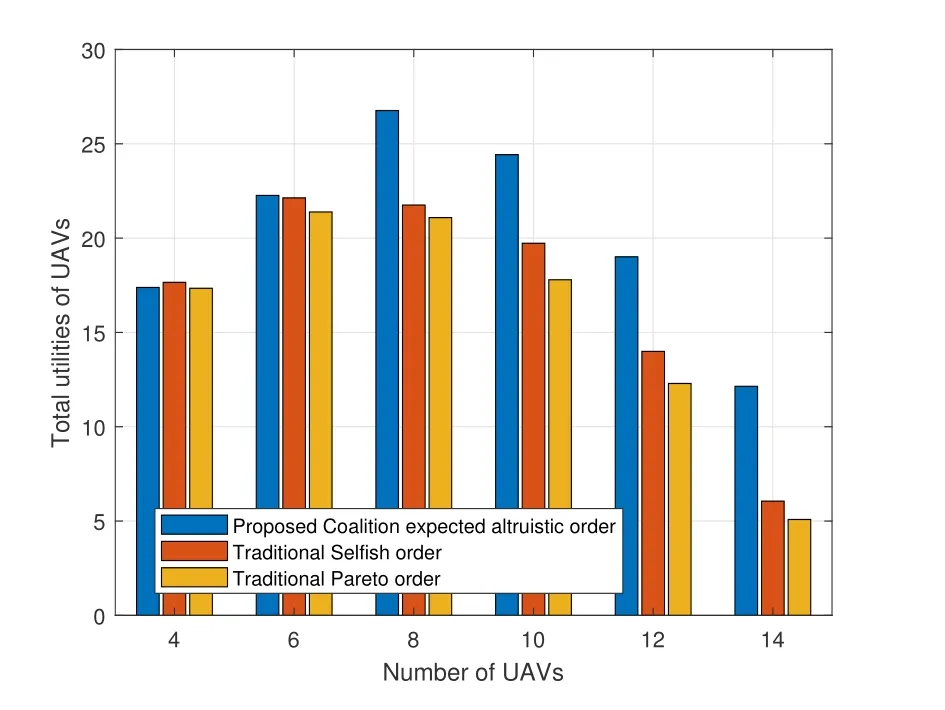
Figure10.The comparison results versus number of UAVs.

5.1 Integration of Multiple Game Models

It is noted that each game model is not capable of addressing all aspects of challenges in resource management for large-scale UAV communication networks.However,when combining more than one game models,the solution of multiple aspects of challenges is expected to be possible.In such framework,some new challenges may arise.For instance,the design of utility function should satisfy the requirements of the new game structure.Moreover,utility function should have physical meaning and try to make the equilibrium of the formulated game correspond to the optimal solution of the original optimization problem.Although there may exist new challenges,it is still a significant and bright future direction.

5.2 Local Adjustment Mechanism of Decision Making

Most researches assume that the topologies of UAV communication networks are static.In addition,although there exists some work where the network topology may change rapidly and dynamically due to the high mobility of UAVs,the failures of existing UAVs and injections of new UAVs are still the research gap.When these situations occur,one applicable method is to re-optimization of the whole network.It might be acceptable if the network is relatively small and the convergence speed is fast.However,it is not possible for large-scale UAV communication networks where re-optimization may consume considerable time.Therefore,local adjustment mechanism of decision making is urgently needed.That is,how to achieve local or global optimum through local adjustment.From game-theoretic perspective,the mechanism can be divided into two aspects.First,when the failure occurs,how to change the local decision making to reach equilibrium again? Second,when injection occurs,what is its decision making and how to reach equilibrium through local adjustment?To summarize,how to reach equilibrium again on the basis of original equilibrium is an interesting yet challenging problems in future research.

5.3 Including Offline Knowledge Base into Online Learning Algorithm

The dynamic and autonomous nature of UAVs makes online decision-making more applicable in UAV communication networks.As more and more UAVs are expected to be applied in the future,the multidimensional resource optimization,e.g.,spatial domain,frequency domain,time domain and energy domain,makes the network more complex.However,multi-dimensional resource optimization leads to huge decision-making space and inefficient online learning.According to the specific control methods and network topology of UAV,modeling for several typical scenarios as the offline knowledge base is a feasible way.When actual scenarios conform to pre-configured or similar scenarios,fast and robust decision making can be obtained with aid of offline knowledge base.

VI.CONCLUSION

In this article,we investigate the distributed resource management problem for large-scale UAV communication networks,which can provide cost-effective and reliable applications in both military and civilian domains.By exploring the inherent features,the distinctive challenges are discussed.Then,we explore several game-theoretic models that not only combat the challenges but also have broad application prospects.We provide the basics of each game-theoretic model and discuss the potential applications for resource management in large-scale UAV communication networks.Specifically,mean-field game,graphical game,Stackelberg game,coalition game and potential game are included.Finally,we give some future research directions to shed light on future opportunities and applications.

ACKNOWLEDGEMENT

This work was supported by National Key R&D Program of China under Grant 2018YFB1800802,in part by the National Natural Science Foundation of China under Grant No.61771488,No.61631020 and No.61827801,in part by State Key Laboratory of Air Traffic Management System and Technology under Grant No.SKLATM201808,and in part by Postgraduate Research and Practice Innovation Program of Jiangsu Province under No.KYCX190188.