Cryptanalysis and Improvement of a New Certificateless Signature Scheme in the Standard Model

Chenhuang Wu,Hui Huang,Kun Zhou,Chunxiang Xu,*

1 School of Computer Science and Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China

2 Key Laboratory of Financial Mathematics(Putian University),Fujian Province University,Putian 351100,China

3 School of computer,Minnan Normal University,Zhangzhou 363000,China

Abstract:Digital signature,as an important cryptographic primitive,has been widely used in many application scenarios,such as e-commerce,authentication,cloud computing,and so on.Certificateless Public Key Cryptography (PKC) can get rid of the certificate management problem in the traditional Public Key Infrastructure(PKI)and eliminate the key-escrow problem in the identity-based PKC.Lately,a new Certificateless Signature(CLS)scheme has been proposed by Kyung-Ah Shim (IEEE SYSTEMS JOURNAL,2018,13(2)),which claimed to achieve provable security in the standard model.Unfortunately,we present a concrete attack to demonstrate that the scheme cannot defend against the Type I adversary.In this type of attack,the adversary can replace the public key of the signer,and then he plays the role of the signer to forge a legal certificateless signature on any message.Furthermore,we give an improved CLS scheme to resist such an attack.In terms of the efficiency and the signature length,the improved CLS is preferable to the original scheme and some recently proposed CLS schemes in the case of precomputation.

Keywords:certificateless;signature;standard model;attack

I.INTRODUCTION

In 1976,Diffie and Hellman[1]presented Public Key Cryptography(PKC)to solve the problem of key distribution in the network environment.Digital signature as an important cryptographic primitive of PKC and due to its advantages of simultaneously accomplishing integrity,authentication and non-repudiation,has been applied widely in many application scenarios[2-5].

In a public key cryptosystem,each user has a public key as well as a private key corresponding to it.As the name implies,the former is publicly available while the latter is kept secret.The central problem in PKC is authenticating a public key of the user,i.e.,proving the public key belongs to the user,and has not been tampered with or replaced by an adversary.Three main approaches have thus far been proposed for authenticating the public keys of users as follows.The first and most widely used method is to employ PKI where a trusted Certificate Authority(CA)provides a certificate to associate a public key with a user.Hence,before using the public key of a user,the validity of the certificate needs checking.However,it is expensive to employ and manage certificates,as shown in[6].In order to settle the issue of certificate management,Shamir [7]offered a new kind of PKC,named Identity-Based PKC(IB-PKC).This is the second approach for authenticating the public key of the user.In IB-PKC,the user's public key is the unique message that can identify her or him(e.g.,Internet Protocol address,or the e-mail address,etc.),and is supposed to be publicly known.Thus,in IB-PKC,the user's public key does not require a certificate to be authenticated,so the problem of certificate management in PKI is eliminated.From then on,IB-PKC has garnered considerable research interest for its merits,and a wealth of identity-based schemes have been presented subsequently,such as in [8-10].In IB-PKC,the Private Key Generator(PKG),a trusted third party,generates the user's private key.However,this method results in another problem to IB-PKC called the key escrow problem because PKG alone generates the user's private key and sends to him/her through a safe way.To address these drawbacks in the traditional PKI and IBPKC,Al-Riyami and Paterson proposed Certificateless PKC (CL-PKC) [11].This is the third approach for authenticating a user's public key.In CL-PKC,the Key Generation Center(KGC),a semi-trusted third party,generates the partial-private-key for a user that is a signature on the user's identity by the KGC.The user selects a secret value to generate his/her public key and the full private key derived from the partial private key and the secret value.Therefore,the KGC cannot access the complete private key of the user in CL-PKC.This eliminates the problem of key escrow in IB-PKC and the problem of certificate management in traditional PKI.

In the attack model of CL-PKC,two types of adversary named Type I adversary(denoted byAI)and Type II adversary(denoted byAII)respectively,need to be considered as discussed in[11,12].In CL-PKC,unlike the authentication method of public key in PKI and IB-PKC,there is no certification for authenticating the public key of a user which results in the condition that the public key replacement attack must be considered and such an attack is referred as Type I attack that is launched byAI.The Type II attack can be seen as the KGC attack,which aims to model a semihonest KGC who tends to pretend as a user because KGC also possesses the partial private key of the user.However,the KGC is not permitted to replace a user's public key,otherwise,the KGC also can generate the full private key of the user which violates the starting point of CL-PKC.Certificateless Signature(CLS)gains advantage of both the CL-PKC and digital signature.From the point of security,a CLS must be able to withstand both types of attacks.Because of the merits of CL-PKC,CL-PKC has been paid much attention to it in recent years[13-20].

As for the security proof of CLS schemes,they may be discussed in the standard model or in the random oracle model.In the random oracle model,cryptographic hash functions will be used during the design of CLS schemes and such hash functions can been seen as random oracles in the process of proof.However,in [21,22],the authors indicated when the random oracles are substituted by a concrete hash functions in the security proof,the cryptography schemes may be insecure.Therefore,more and more researchers turn their attention to the standard model.Inspired by Paterson-Schuldt's IBS scheme [23],the first provably secure CLS scheme in the standard model was proposed in [24].Unfortunately,the CLS scheme in[24]has been attacked by Xiong et al.[25].More specifically,the CLS scheme can suffer from the malicious-but-passive KGC attack.In the literature,there are many CLS schemes that were certificated secure in the standard model,but these CLS schemes are based either on the Waters'technique proposed in[26]or on the generic conversion technique proposed in [27].However,because of the cumbersome construction,the efficiency of these CLS schemes is relatively low.In [28],S´ebastien et al.introduce a new way to construct a CLS scheme whose security can be proved in the standard model.

Recently,to improve the efficiency of the CLS scheme in standard model,Shim[29]presented a new CLS and asserted that the CLS was secure in the standard model,that is,Shim claimed that the CLS could resist the two types of attack.However,in this paper,we show that Shim's CLS is not secure since it can be attacked byAI.More precisely,AIcan fabricate a legal CLS on any messagemby performing a replacement public key of a target user.In addition,we give an improved CLS scheme to overcome such an attack.The efficiency and signature length of the improved scheme is preferable to Shim's CLS in[29].

The structure of this paper is as follows.Section II gives some preliminaries for the paper.Section III briefly reviews Shim's CLS scheme.Section IV analyzes the security of Shim's CLS scheme and gives a concrete attack method on it.Section V puts forward an improved scheme.Then,security and efficiency analysis are briefly discussed in section VI.Finally,Section VII concludes the paper.

II.PRELIMINARIES

In the section,we give the description of some symbols in Table1 used in the paper,and the definition of bilinear parings,difficult problem assumptions,CLS scheme and its security model.

Table1.Notations

(1)Bilinear pairings.

LetG1andG2be multiplicative cyclic groups with the same prime orderpandgis a generator ofG1.e:G1×G1→G2is a bilinear map which satisfies the following properties.

1) Bilinearity:e(gx,gy)=e(g,g)xyfor allx,y ∈Zp.

2) Nondegeneracy:There areu,v ∈G1such thate(u,v)/=1G2,where 1G2denotes the identity element ofG2.

3)Computability:For allu,v ∈G1,e(u,v)can be efficiently computed.

Tate pairing and the modified Weil pairing are the admissible maps of this kind.Please refer to[30]for more details.

(2)Hard problem assumptions.

We describe some hard problems which will be used in the paper.Letgbe a generator ofG1with orderp.These problems are as follows.

1) Discrete problem (DLP).Given (g,gx),to computex,wherex ∈Z∗p.

2) CDH problem (CDHP).Given (g,gx,gy),to computegxy,wherex,y ∈Z∗p.

3) Inverse-CDH problem (ICDHP).Given (g,gx),to computegx−1,wherex ∈Z∗p.

4) Combined-Inverse-CDH problem (CICDHP).Given (g,gx,w),to computewx−1,wherex ∈Z∗p,w ∈G1.

It is widely believed that the CDH problem and Inverse-CDH problem are hard which have been used to design a lot of cryptographic schemes.For Combined-Inverse-CDH problem,it is easy to see thatwx−1can be directly derived from Inverse-CDH problem (g,gx) and CDH problem (g,gx−1,w).Therefore,we can believe that the Combined-Inverse-CDH problem also is hard.

(3)Definition of CLS scheme.

A CLS scheme consists of five algorithms:Setup,Partial-Private-Key-Extract,User-Key-Generation,CL-Sign and CL-Vfy.The details are as follows.

1) Setup:Given a security parameterk,the algorithm outputs a master secret keymsk,a corresponding master public keympkand some publicly known system parameters.

2)Partial-Private-Key-Extract:Given a user's identityID,the system master secrete keymsk,and some system parametersIP,the algorithm outputs a partial private keyparkeyIDfor the userID.

3) User-Key-Generation:Given a user's identityIDand the partial private keyparkeyID,the algorithm outputs a secret keyuskIDand a corresponding public keyupkIDfor the userID.Then,the public keyupkIDis made publicly known andSKID=(parkeyID,uskID) is the full private key of the userIDwhich is only known to the user.

4)CL-Sign:Given a private keySKIDof userID,a messagem,a user public keyupkID,and some other optional informationIS,the algorithm outputs a signatureσ.

5)CL-Vfy:Given an identity ofIDa user,a messagem,a user public keyupkID,a signatureσ,and some other optional informationIS,the algorithm outputs Valid if CL-Vfy(m,ID,upkID,IS,σ)=1,or⊥otherwise.

(4)Security models of CLS scheme.

Five oracles can be accessed by the adversaries.

Then the little mermaid raised her lovely white arms, stood on the tips of her toes, and glided94 over the floor, and danced as no one yet had been able to dance

Create-User:On input an identityID,ifIDhas already been created,nothing needs to be executed by the oracle.Otherwise,the oracle executes the algorithm Partial-Private-Key-Extract and User-Key-Generation to generate the public keyupkIDand the full private keySKID=(parkeyID,uskID).

Reveal-Partial-Private-Key:On input an identityID,it returns the corresponding partial private key if theIDhas been created.Otherwise,it makes a Create-User query to getparkeyIDand then returns it.

Reveal-User-Secret-Key:On input an identityID,it returns the corresponding secret key if theIDhas been created.Otherwise,it makes a Create-User query to getuskIDand then returns it.

Replace-Public-Key:On input an identityIDwith the new public keyupk′IDand corresponding new secret keyusk′ID,if the userIDhas been created,then the user's original public key and corresponding secret key will be respectively replaced byupk′IDandusk′ID.Otherwise,nothing needs to be done.

CL-Sign:On input a messagem,an identityIDand public keyupkID,the oracle responds to it according to one of the following three cases:

1) IfIDhas not been created,then it getsupkIDandSKIDby making query to Create-User and returnsσ ←CL-sign(SKID,m,IS).

2)IfIDhas been created and his public keyupkIDand secrete keyuskIDhave not been replaced,then it returnsσ ←CL-Sign(SKID,m,IS).

3) IfIDhas been created and his public key and secrete key have been respectively replaced withupk∗IDandusk∗ID,then it returnsσ ←CL-Sign(SK∗ID,m,IS).(If the signatureσ∗is not valid,the oracle can run a scheme specific“knowledge extractor”to obtain a valid signature.)

Game I:LetCIbe a challenger who will play this game withAIin the following steps.

1)CIcarries out the Setup algorithm to get the system parameters Params and a master public keympkand then sends them toAI.

2)AIcan make queries to the five oracles:Create-User,Reveal-Partial-Private-Key,Reveal-User-Secret-Key,Replace-Public-Key,and CL-Sign which are executed byCIduring the simulation.

3) Finally,AIoutputs a forgery (σ∗,m∗,upk∗ID,ID∗).Then,AIwins the Game I if all the following conditions hold:

1)CL-Vfy(mpk,ID∗,upkID∗,m∗,ID∗)=1.

2) The tuple (m∗,ID∗,upk∗ID) has never been queried to CL-Sign.

3)ID∗has never been queried to Reveal-Partial-Private-Key.

Game II:LetCIIbe a challenger who will play this game withAIIin the following steps.

1)CIIcarries out the Setup algorithm to get the system parameters Params and a master public keympkand master secrete keymskand then sends them toAI.

2)AIIcan make queries to the four oracles:Create-User,Reveal-Partial-Private-Key,Reveal-User-Secret-Key,and CL-Sign which are executed byCIIduring the simulation.

3) Finally,AIIoutputs a forgery (σ∗,m∗,upk∗ID,ID∗).Then,AIIwins the Game II if all the following conditions hold:

a)CL-Vfy(mpk,ID∗,upkID∗,m∗,ID∗)=1.

b) The tuple (m∗,ID∗,upk∗ID) has never been queried to CL-Sign.

c)AIInever queried withID∗to Reveal-User-Secret-Key.

We say that a CLS scheme is secure ifAIandAIIcan not win the Game I and Game II,respectively.

III.REVIEW OF SHIM'S CLS SCHEME

In the following,we will review Shim's scheme in [29]briefly,which consists of five algorithms:Setup,Partial-Private-Key-Extract,User-Key-Generation,CL-Sign and CL-Vfy.

Setup:Given a security parameterk,KGC selects two secure hash functionsHu:{0,1}∗→{0,1}nuandHm:{0,1}∗→{0,1}nmwherenu,nm ∈Z+,a bilinear paringe:G1×G1→G2whereG1andG2are multiplicative cyclic groups with the same prime orderpandgis a generator ofG1.KGC picks random valuesα∈RZ∗p,g2,g3∈RG1and setsg1=gα,W=e(g1,g2).KGC randomly chooses the following elements:u′,m′∈RG1,∈RG1,i=1,...,nu;∈RG1,j=1,...,nm.Let ˆU={}and={}.The system public parameters are params=〈p,G1,G2,e,g,g1,g2,g3,u′,,m′,,W〉and the system master key isgα2.

Partial-Private-Key-Extract:Given a user's identityID,KGC computes u=Hu(ID).Letu[i]be theith bit of u andU ⊂{1,...,nu}be the set of indices such that u[i]=1.KGC randomly choosesru∈RZ∗pat first and then computesparkeyIDas the partial private key for userID,whereparkeyID=(psk(1),psk(2))=

User-Key-Generation:Given a user's identityID,the userIDexecutes this algorithm to pickτ,x∈RZ∗pand then computesupkID=(pk(1),pk(2))=(gτ,gx)∈G1× G1as his (or her) public key and the corresponding secret key isuskID=(τ,x).

CL-Sign:Given a signer's identityID,partial private keyparkeyID,secret keyuskID,public keyupkIDand a messagem,the signer computes m=Hm(m,ID,upkID).Let m[i]be theith bit of m andM ⊂ {1,...,nm}be the set of indicesisuch that m[i]=1.The signer choosesr,k∈RZ∗pand computesσ=(σ1,σ2,σ3),where

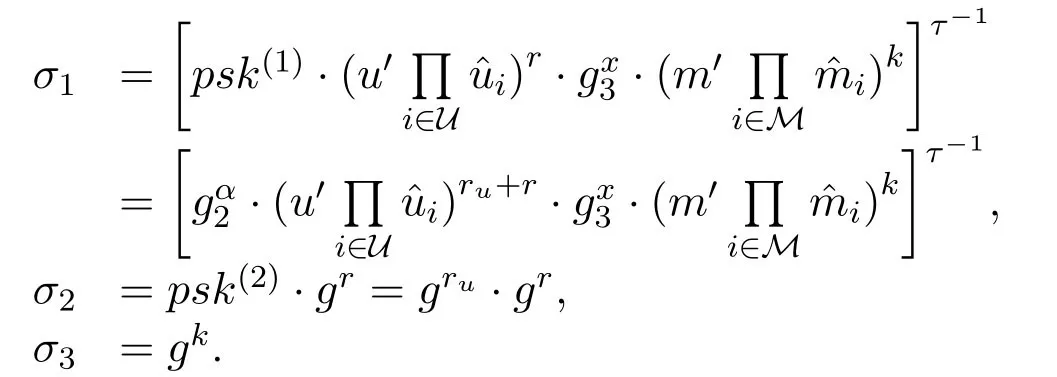
CL-Vfy:Given a signatureσ=(σ1,σ2,σ3) for{ID,upkID}on a messagem,the verifier computes m=Hm(m,ID,upkID)and verifies whether the following equation holds or not

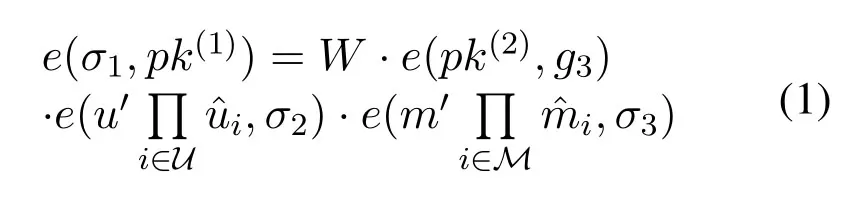
If the Eq.(1) is satisfied which indicates that the signatureσ=(σ1,σ2,σ3)on messagemis valid.Otherwise,it is invalid.

IV.CRYPTANALYSIS OF SHIM'S CLS SCHEME

In [29],the author claimed the CLS scheme was existentially unforgeable againstAIandAII.Unfortunately,in this section,we show that the CLS scheme in[29]can suffer from the Type I attack.Without loose of generality,we denoteID∗be the identity of a target user thatAIwill attack on it.In such an attack,AIreplaces the public key of a target userID∗and then forge a legal signature on any selected messagem∗by himself.AIexecutes the attack process as follows.

1)computes u∗=Hu(ID∗).LetU∗⊂{1,...,nu}be the set of indices such that u∗[i]=1.

2) choosesτ′,x′∈RZ∗p,letupk′ID∗takes the place of the public key of the target user withID∗,and

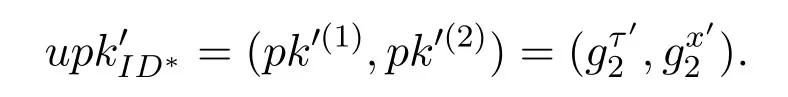
3)choosesr′,k′∈RZ∗pand sets

4) computes m∗=Hm(m∗,ID∗,upk′ID∗).Let m∗[i]be theith bit of m∗andM∗⊂{1,...,nm}be the set of indicesisuch that m∗[i]=1.

5)sets

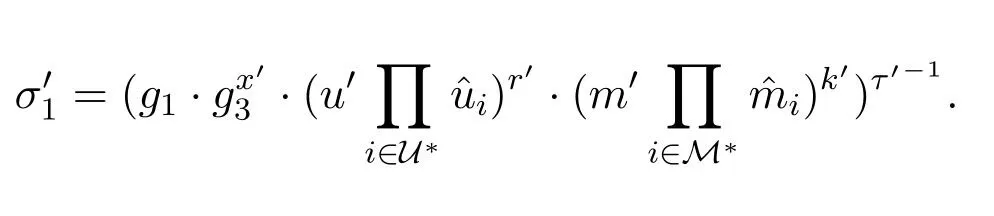
We note that

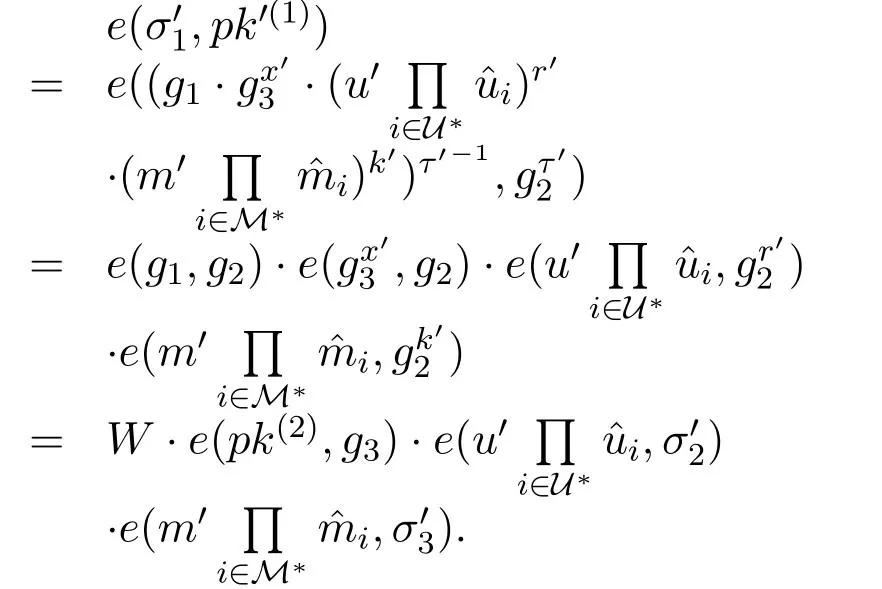
Therefore,the signatureσ′=(σ′1,σ′2,σ′3)of the target userID∗which was forged byAIon messagem∗satisfies the Eq.(1),and hence the signature is valid.We get the result that the CLS scheme proposed in[29]is insecure under the Type I attack.Therefore,there must be some mistakes in the proof of the scheme presented in[29].We note that in the Replace-Public-Key Queries of Theorem 1 in[29],whenAIrequests to replace the public key of a user,AIis required to provide the logarithm of the new public key with respect togwhich actually is the user's private key.Thus,this proof method does not include the condition of our attack,because in our attackAIdoes not have the knowledge of the logarithm of the new public key with respect tog.

V.THE IMPROVED SCHEME

As it is shown in the previous section,a user's public keyupk=(pk(1),pk(2))=(gτ,gx) can be replacedFrom the concrete attack method shown in the above section,we can see the basic reason why the Type I adversaryAIcan successfully forge a legal CLS.That is,there is no need forAIto get the discrete logarithm of the replaced public keypk′(1)andpk′(2)with respect tog.In fact,as described in [29],the discrete logarithms of a user's public keypk(1)andpk(2)with byAIwith the respect togare the secret key of the user.Therefore,in order to overcome this attack,a verifier must be convinced that the signer knows the discrete logarithm of the signer's public key with respect tog.To achieve this goal,we provide a description of our improved scheme as follows.

Setup:As the original scheme in [29],the public parameters are

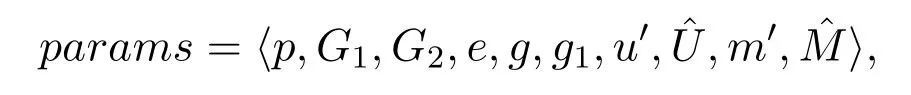
and the master key isα.

Partial-Private-Key-Extract:Given a user's identityID,KGC computes u=Hu(ID).Let u[i]be theith bit of u andU ⊂{1,...,nu}be the set of indices such that u[i]=1.KGC computesparkeyID=Set the userID's the partial private key asparkeyID=

User-Key-Generation:Given a user's identityID,the userIDcomputes u=Hu(ID),picksτ∈RZ∗p,sets his(or her)public key as

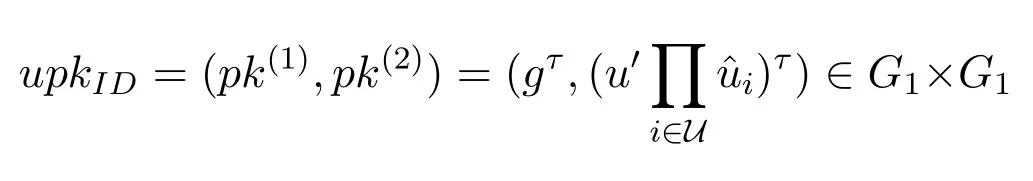
and sets his(or her)secret key asuskID=τ.

CL-Sign:Given a signer's identityID,partial private keyparkeyID,secret keyuskID,public keyupkIDand a messagem,the signer generates a CLS signatureσ=(σ1,σ2)as follows.

1)choosesk∈RZ∗pand computesσ2=gk.

2) computes m=Hm(m,ID,upkID,g1,σ2).Let m[i]be theith bit of m andM ⊂{1,...,nm}be the set of indicesisuch that m[i]=1.

3)setsσ1=

CL-Vfy:Given a signatureσ=(σ1,σ2) for{ID,upkID}on a messagem,the verifier computes m=Hm(m,ID,upkID,g1,σ2),u=Hu(ID),M,Uand verifies whether the following two equations are satisfied at the same time.

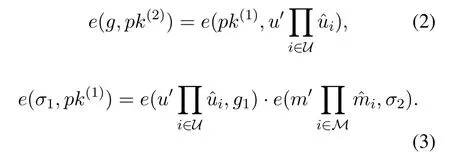
Now,we demonstrate that the signatureσ=(σ1,σ2) on messagemgenerated from the CL-Sign algorithm can satisfy the Eq.(2)and(3),respectively.

VI.SECURITY AND EFFICIENCY ANALYSIS

In this section,we will give a sketch proof for the security of the improved CLS scheme in the Section V.The sketch security analysis for the improved scheme againstAIattack andAIIattack are as follows.

Theorem 1.If the CDH problem is hard,then the improved scheme can resist the AI attack.

Proof.(sketch) By contradiction,if the adversaryAIcan win the Game I,i.e.AIsuccessfully forge a signature,then the CDH problem will be solved byCI.Assume that (g,ga,gb) is a CDH problem instance,then we prove thatCIcan use the forge ability ofAIto solve the CDH problem.First,CIinitializes the system parameters and sets the system public key asg1=ga.Since the system parameters in Game I are generated byCI,so in order to makeCIeasily simulate the queries fromAI,we assume here thatCIcan choose a user's identityID∗such thatThen,CIsets the public key of the userID∗aswhereIt is easy to see that,upkID∗=satisfies Eq.(2) Now,CIandAIbegin to play the Game I.CIanswers the queries fromAI.Finally,we assume thatAIwins the Game I,i.e.,it successfully generates a signatureσ∗=(σ∗1,σ∗2)on messagem∗with respect to the identityID∗.That is,σ∗=(σ∗1,σ∗2)can satisfy Eq.(3),i.e.,

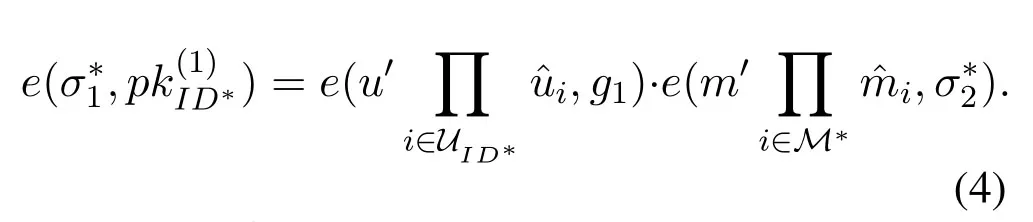
Letσ∗2=gkandkis known toCI.Then,with the help ofAI,i.e.,AIalso sendsktoCI.Therefore,from Eq.(4),we note that

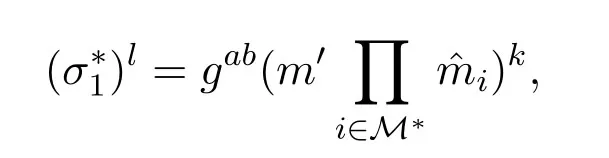
thenCIcan computewhich is the solution of the CDH problem instance(g,ga,gb).This is contradict to the CDH problem which is hard.That is,there is no adversaryAIcan win the Game I,i.e.,the improved scheme can resist theAIattack.We complete the proof.

Theorem 2.If the Combined-Inverse-CDH problem is hard,then the improved scheme can resist attack.

Proof.(sketch) Similar to the proof of Theorem 1.Also by contradiction,if the adversaryAIIcan win the Game II,i.e.AIIsuccessfully forge a signature,then the Combined-Inverse-CDH problem will be solved byCII.Assume that(g,gt,A),A ∈G1is a Combined-Inverse-CDH problem instance,then we prove thatCIIcan use the forge ability ofAIIto solve the Combined-Inverse-CDH problem.First,CIIinitializes the system parameters and choosesα ∈Z∗pas the system mater key,gαas the system public key.CIIsends the system parameters and the system mater key toAII.Therefore,AIIcan generate each user's partial private key.Since the system parameters in Game II are generated byCII,so in order to makeCIIeasily simulate the queries fromAII,we assume here thatCIIcan choose a user's identityID∗such thatu′·Then,CIIsets the public key of the userID∗as

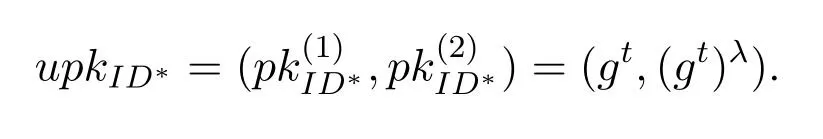
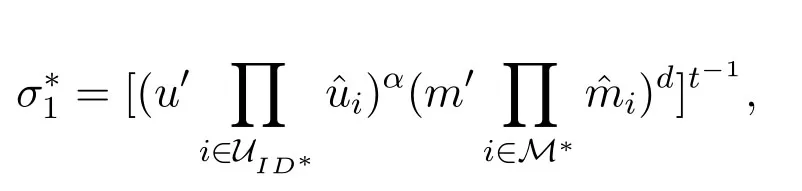
thenCIIcan computeσ∗1which is the solution of the Combined-Inverse-CDH problem instance (g,gt,A),whereThat is,σ∗1=At−1is the solution of the Combined-Inverse-CDH problem instance (g,gt,A).This is contradict to the Combined-Inverse-CDH problem which is hard.We complete the proof.

Theorem 3.The improved CLS scheme is secure.

Proof.From the above Theorem 1 and Theorem 2,we can see that the improved CLS scheme in Section V can resist theAIattack andAIIattack at the same time.Therefore,the improved CLS scheme is secure.Now,we compare the efficiency of the improved scheme with it of [29]and two recently presented CLS scheme in the standard model [31,32].When the pre-computations are respectively considered in the CL-Sign,CL-Vfy algorithms of [29,31,32]and our improved scheme.For example,we find that the bilinear pairing computationse(pk(2),g3) in Eq.(1),e(g,pk(2)) andin Eq.(2),and in Eq.(3) can be pre-computed because these bilinear pairings are independent of the messagem.In the following part,we list some symbols for the computations used in the scheme.Let Exp and Mul be exponentiation and multiplication inG1,respectively.Let Inv be the inversion inZ∗p.Let M be the multiplication inG2.Let Par be the bilinear pairing computation which is the most time-consuming computation in elliptic curve cryptography.|G1|denotes the length of element inG1.From Table2,we can see that the improved CLS is preferable to the CLS in[29,31,32].

For quantitative computation comparison reasons,we use the experiment result in[33].By choosing the Type A pairing using PBC library [34]on ThinkPad T430s which is equipped with an Intel Core i5-3210M2.5 GHz machine with 4G RAM.Then,the experiment results show that every inversion (Inv) inZ∗pneeds 0.004ms,every point multiplication(Mul)inG1needs 8.006 ms,every exponentiation (Exp) inG1needs 1.882 ms,every multiplication(M)inG2needs 0.013 ms,and every pairing operation(Par)needs 16.064ms,respectively.Then,replacing these data into the Table2,we show the efficiency of CL-Sign,CL-Vfy algorithms in[29,31,32]and ours in Figure1,respectively.

Table2.The comparison of efficiency and signature length

Figure1.CL-Sign and CL-Vfy time of the four schemes

When we consider the total time of CL-Sign and CL-Vfy algorithms for each scheme in [29,31,32]and ours,the trend of change in the efficiency of them with the increase of the number of signatures can be represented in Figure2.

From Figure1,Figure2 and Table2,we can see that our improved scheme is more efficient than other three CLS schemes[29,31,32]and the length of signature is the shortest.

VII.CONCLUSION

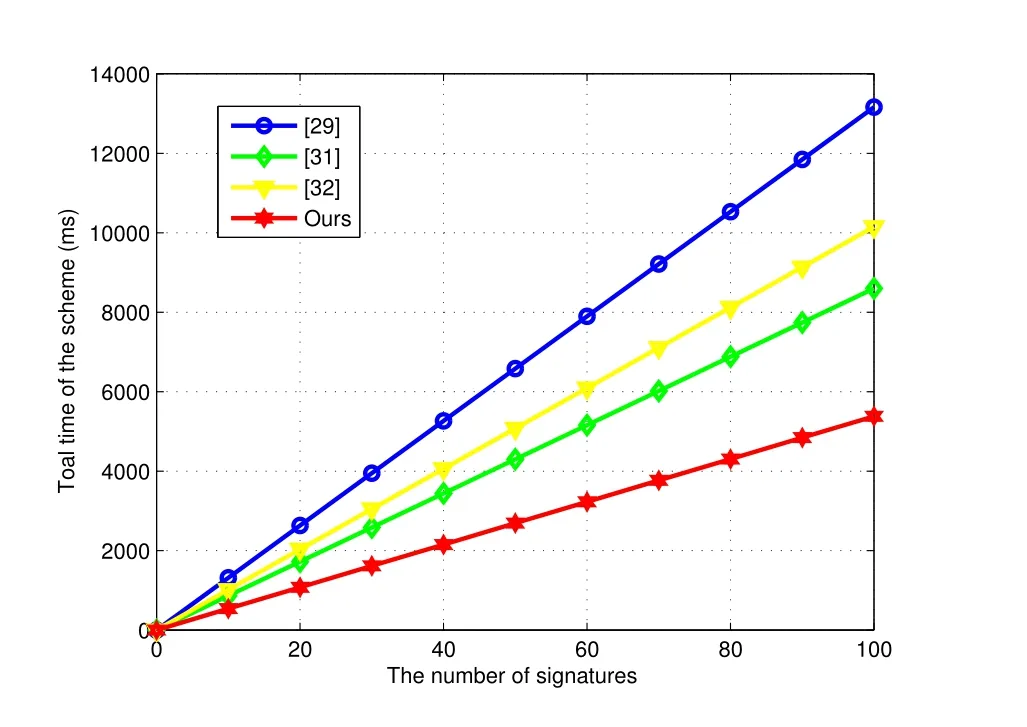
Figure2.Computational time of the four schemes

Recently,a CLS scheme with its' security proved in the standard model was proposed by Shim in[29].However,after the cryptanalysis of Shim's CLS scheme,we find that Shim's CLS scheme has security problems,that is,it cannot resist the attack ofAI.Furthermore,after analyzing the basic reason for the existence of the attack,we present an improved method to improve the CLS scheme to resist such an attack.In terms of the precomputation,when we compare the improved CLS scheme with Shim's CLS scheme [29]and some other CLS schemes [31,32],the results show that the efficiency of the improved CLS scheme is the highest one among these four CLS schemes.Additionally,the improved CLS scheme also has the shortest signature length among these four CLS schemes.In recent years,CLS as a cryptographic primitive and due to its merits,more and more researchers have been dedicated to the study of CLS schemes in industrial application,such as in Internet of Things(IoT)[35,36],in Internet of Vehicles(IoV)[37,38],in Wireless Body Area Networks (WBAN)[39,40],and so on.Thus,our improved scheme can be used for these application scenarios.Additionally,we can also design some other CLS schemes according to kinds of application scenarios.Furthermore,designing some CLS with specific properties also is a research direction[41,42].

ACKNOWLEDGEMENT

The work was partially supported by the National Natural Science Foundation of China under grant Nos.61872060 and 61772292,the National Key R&D Program of China under grant No.2017YFB0802000,Key Laboratory of Financial Mathematics of Fujian Province University (Putian University) under grant Nos.JR201806 and JR201901,by the Natural Science Foundation of Fujian Province under grant Nos.2019J01752 and 2020J01905,by the Program for Innovative Research Team in Science and Technology in Fujian Province University under grant No.2018-049,by the Educational Research Projects of Young and Middle-aged Teachers in Fujian Education Department(JAT200514).