Joint Trajectory and Power Optimization for Securing UAV Communications Against Active Eavesdropping

Bin Duo,Junsong Luo,*,Yilian Li,Hao Hu,Zibin Wang

1 College of Information Science and Technology,Chengdu University of Technology,Chengdu 610059,China

2 National Key Laboratory of Science and Technology on Information System Security,Beijing 100093,China

Abstract:Due to both of jamming and eavesdropping,active eavesdroppers can induce more serious security threats to unmanned aerial vehicle (UAV)-enabled communications.This paper considers a secure UAV communication system including both the downlink(DL)and uplink(UL)transmissions,where the confidential information is transmitted between a UAV and a ground node in the presence of an active eavesdropper.We aim to maximize the average secrecy rates of the DL and UL communications,respectively,by jointly optimizing the UAV trajectory and the UAV/ground node's transmit power control over a given flight period.Due to the non-convexity of the formulated problems,it is difficult to obtain globally optimal solutions.However,we propose efficient iterative algorithms to obtain high-quality suboptimal solutions by applying the block coordinate descent and successive convex optimization methods.Simulation results show that the joint optimization algorithms can effectively improve the secrecy rate performance for both the DL and UL communications,as compared with other baseline schemes.The proposed schemes can be considered as special cases of UAV-assisted non-orthogonal multiple access(NOMA)networks.

Keywords:UAV communications;active eavesdropping;physical-layer security;secrecy rate maximization;power control;trajectory design

I.INTRODUCTION

With the advantages of low cost,high mobility,rapid deployment and wide coverage,unmanned aerial vehicles (UAVs) play an important role in many practical scenes,such as wireless sensor networks [1],disaster rescue [2]and aerial photography [3].In particular,in wireless communication systems,the application of UAVs can effectively improve the throughput[4],enhance the security performance[5]and expand the communication distances [6],etc.However,although the line-of-sight(LoS)dominant transmission provides better communication quality in UAV communications,it is also extremely vulnerable to serious security threats such as eavesdropping,jamming and truncation caused by illegal communication nodes on the ground.This leads to the confidential information leakage and communication quality degradation.Therefore,how to ensure the security of information transmission in UAV communication systems has become a challenging issue.

By taking advantage of their flexible flying trajectory,UAVs can establish favorable transmission conditions for legitimate communications over malicious ground nodes.Therefore,the UAV trajectory design combined with physical-layer security technique can effectively improve the secrecy rates in UAV communications [7,8].A three-node secure UAV-enabled communication system was first considered in [9],where the joint optimization of the UAV trajectory and power control was proposed to improve the secrecy rates.The authors in[10]proposed an aerial cooperative jamming scheme for improving the secrecy performance of the ground wiretap channel,with the UAV being a friendly jammer to interfere with the potential eavesdropper.Based on the idea of the aerial cooperative jamming,a novel dual-UAVs communication system was proposed in [11],where one UAV transmits private information to ground nodes while the other UAV helps to interfere with eavesdroppers for enhancing the secrecy rates.To provide communication services for ground nodes with long distances,a UAV-aided relaying wireless network with caching was proposed in [12],where the UAV trajectory and time scheduling are jointly optimized to enhance the secrecy rate performance.Non-orthogonal multiple access (NOMA) as a promising technique can effectively enhance the spectral efficiency for wireless communication systems [13,14].Therefore,the UAVaided NOMA networks were studied in[15]and a corresponding joint precoding optimization scheme was proposed to maximize the throughput of ground users while guaranteeing the system security via artificial jamming.In [16],a secure downlink UAV communication scheme enabled by NOMA was proposed to maximize the minimum achievable secrecy rate by the joint optimization of the user scheduling,power allocation and trajectory design.

However,with the rise of full-duplex technology,active eavesdropping brings more serious security threats to UAV communication systems.It cannot only send jamming signals to legitimate nodes for hindering them from obtaining valid and reliable information,but also wiretap the confidential information from UAV communications.Therefore,it is more practical to study the secure UAV communication in the presence of active eavesdroppers.The works in[17,18]proposed artificial noise (AN) methods for safeguarding the UAV communications against fullduplex active eavesdroppers,where the power allocations of the AN and transmit signals as well as the UAV altitude are jointly optimized to improve the rate performance.Note that the above works do not fully take advantage of the UAV trajectory flexibility to mitigate active eavesdropping.Therefore,it motivates us to investigate whether anti-active eavesdropping trajectory design can further improve the secrecy rate performance of UAV-enabled communications.

In this paper,we consider both the uplink (UL)and downlink(DL)transmissions of the UAV-enabled communication system,where a ground node and a UAV form a legal communication link while an active eavesdropper intends to interfere and intercept the confidential information.Due to the existence of the active eavesdropper,the UAV trajectory should be adjusted to approach the ground user while keeping away from the active eavesdropper for establishing favorable transmission conditions.To safeguard both the UL and DL communications,we aim to maximize the worst-case average secrecy rates with a given UAV flying duration,by jointly designing the transmit power allocation and UAV trajectory optimization algorithms.The optimization problems are subject to the UAV mobility and transmit power constraints.Due to the non-convexity of the formulated problems,it is challenging to obtain globally optimal solutions with feasible complexity.To tackle such difficulties,we first transform the objective functions into achievable lower bound expressions.Then,we propose efficient iterative algorithms to solve the corresponding problems approximately by applying block coordinate descent (BCD) method.In this way,the optimization variables can be divided into two blocks,i.e.,the UAV trajectory and the ground node/UAV transmit power control variables,which are alternately optimized over iterations.However,even with the given transmit power,the subproblems of UAV trajectory optimization are still intractable due to its non-convexity.We thus introduce slack variables and apply the successive convex approximation(SCA)technique to solve them approximately.The numerical results show that the proposed algorithms can significantly improve the secrecy rate performance,comparing with other benchmark schemes,which demonstrates the importance of the joint power control and trajectory design against active eavesdropping in both the DL and UL transmissions in UAV-enabled communications.

The rest of this paper is organized as follows.Section II represents the system model and problem formulation.In Section III and IV,we propose iterative algorithms for DL and UL transmissions,respectively.The numerical results are provided to validate the effectiveness of the proposed algorithms in Section V.Finally,Section VI concludes the paper.

II.SYSTEM MODEL AND PROBLEM FORMULATION

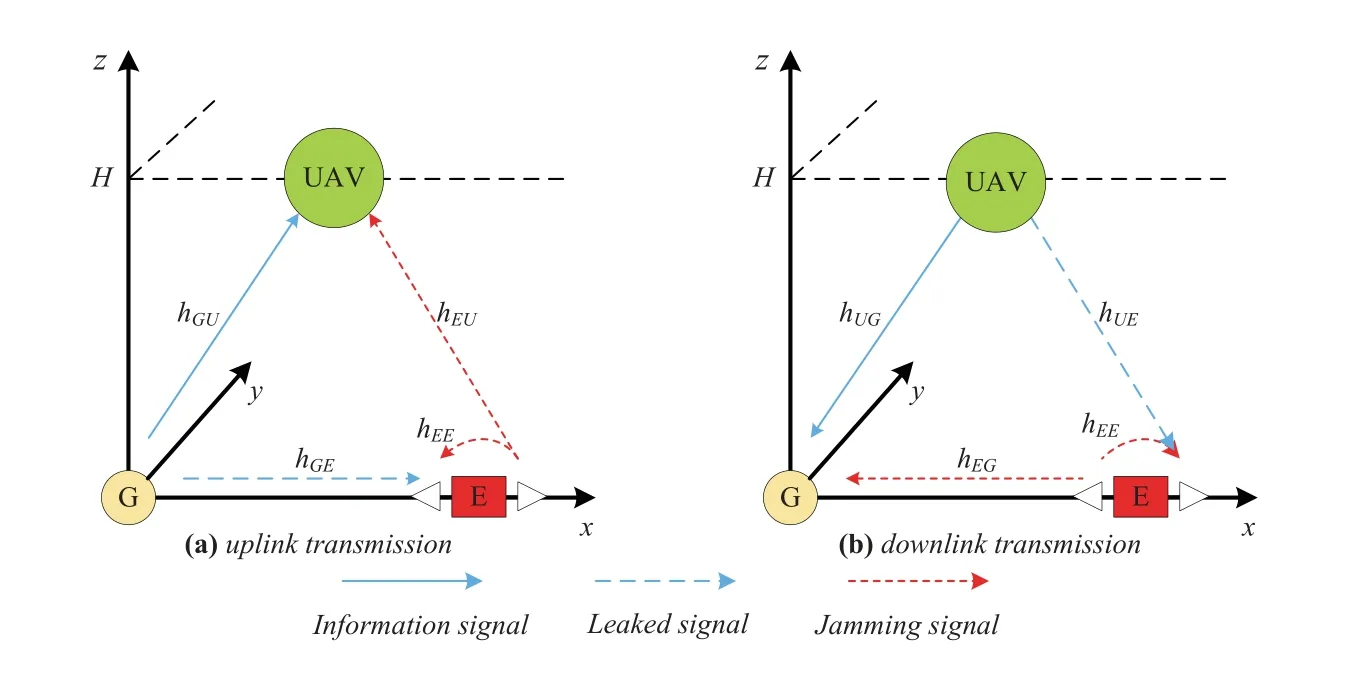
Figure1.Secure UAV communication systems subjected to an active eavesdropper.

2.1 System Model

As shown in Figure1,we consider two secure transmission schemes for UAV-aided communications:the UL transmission where a ground node (G) transmits to a legitimate UAV as well as the DL transmission where a UAV transmits to a legitimate G.Both schemes face severe security issues caused by a fullduplex active eavesdropper(E).The active eavesdropper wiretaps the secrecy information between G and the UAV,meanwhile sending jamming signals to degrade the legitimate transmissions.We establish the three-dimensional (3D) Cartesian coordinate system,where the horizontal coordinates of G and E are denoted by wG=(0,0)and wE=(A,0),respectively,with their locations being known to the UAV1

Within a given finite flight periodT,the UAV flies horizontally from the pre-determined initial location to the final location,which are denoted by q0=(x0,y0)and qF=(xF,yF),respectively,with a fixed altitudeH.To make it more manageable,Tis divided intoNequal-length slots,i.e.,T=δtN,whereδtis the length of a time slot.As such,the UAV trajectory can be denoted as q[n]={x[n],y[n]}Nn=1.Denote byVmaxthe maximum flying speed of the UAV,and thusD=Vmaxδtrepresents the maximum UAV horizontal flying distance in time slotn.Practically,the UAV should satisfy the mobility constraints as follows:

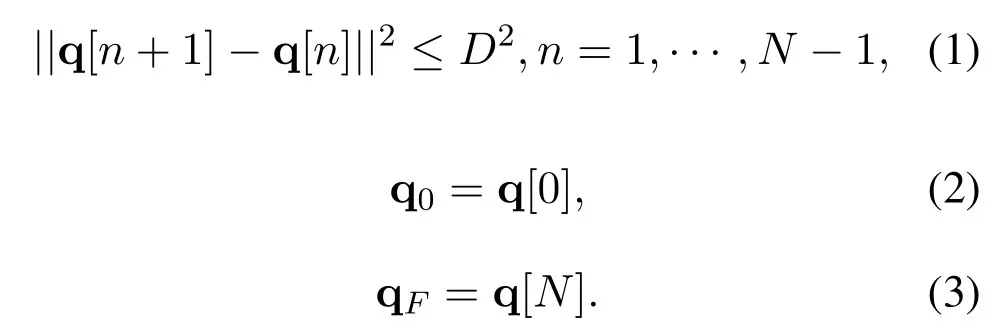
2.1.1 Channel Model of Downlink Transmission

For the transmissions from the UAV to G (UG) and the UAV to E(UE)at time slotn,we assume that the channel power gain follows the free-space path loss model[9-12],which is given by2

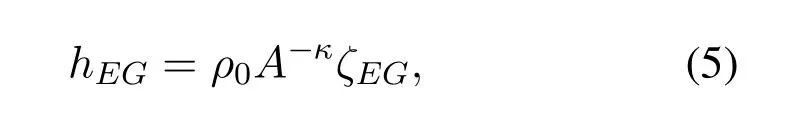
whereκis the path loss exponent andζEGis a random variable with unit mean exponential distribution to characterize small-scale Rayleigh fading.

LetpU[n],anddenote the UAV's transmit power in time slotn,average and peak powers,respectively.In practice,they should satisfy the following constraints,

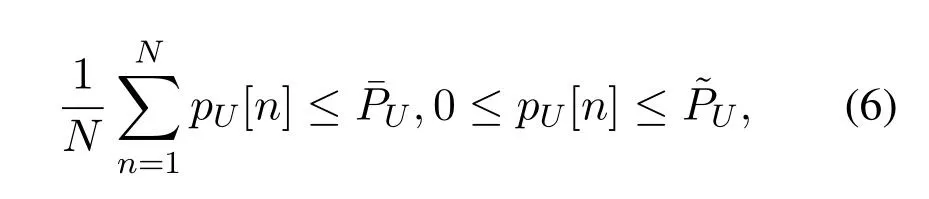
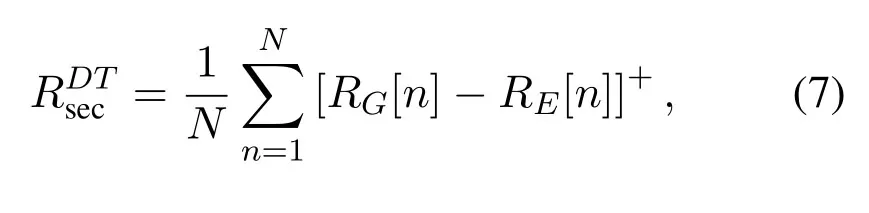
where [x]+=max(x,0).LethEErepresents the self-interference from E's transmitting antenna to its receiving antenna andpEis the maximum transmit power of E.The achievable rates at G and at E in time slotncan be expressed as

where E[·]is the expectation operator with respect toζEGandσ2is the additive white Gaussian noise(AWGN)power at G or E.SinceRG[n]in(8)is convex with respect to its random variableζEG[21],we can derive its lower bound based on Jensen's inequality,i.e.,

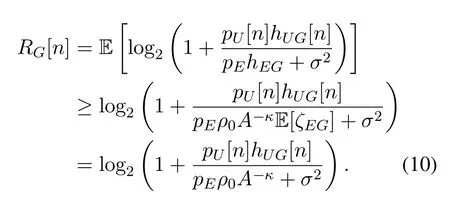
Note that we consider the worst-case secrecy rate performance by assuming that the active eavesdropper transmits with its maximum power over the whole period and it can perfectly cancel its self-interferencehEE.As such,RE[n]in(9)can be upper-bounded by

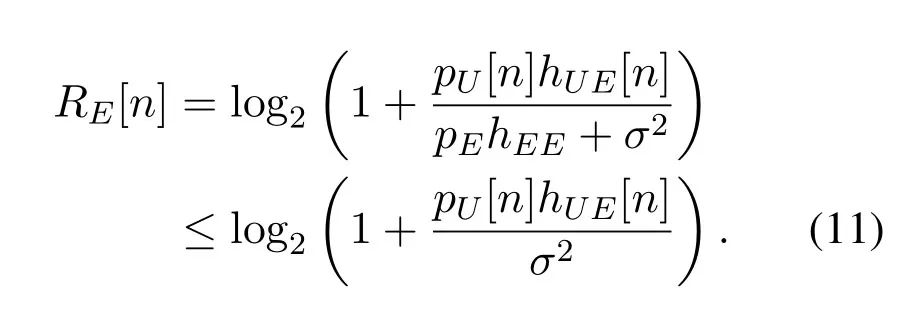
2.1.2 Channel Model of Uplink Transmission

Similarly,for the ground-to-air links between G and the UAV (GU),and E and the UAV (EU) at time slotn,the channel power gain is given by

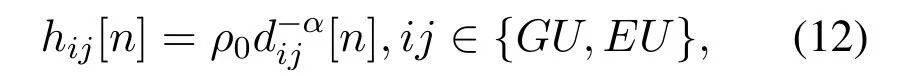
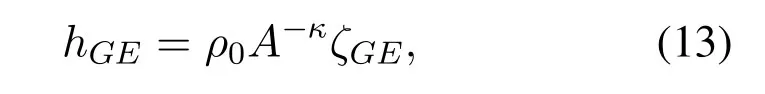
whereζGEis an exponentially distributed random variable.

Denote bypG[n]the transmit power of G in time slotn.Similar to the DL transmission,pG[n]is constrained by average and peak power limits denoted byandrespectively,i.e.,

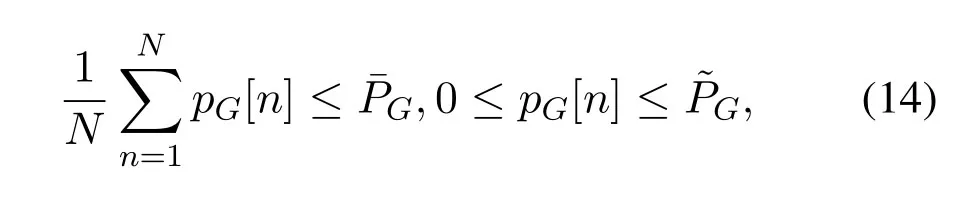
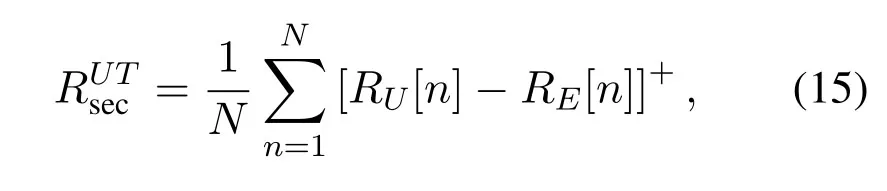
where

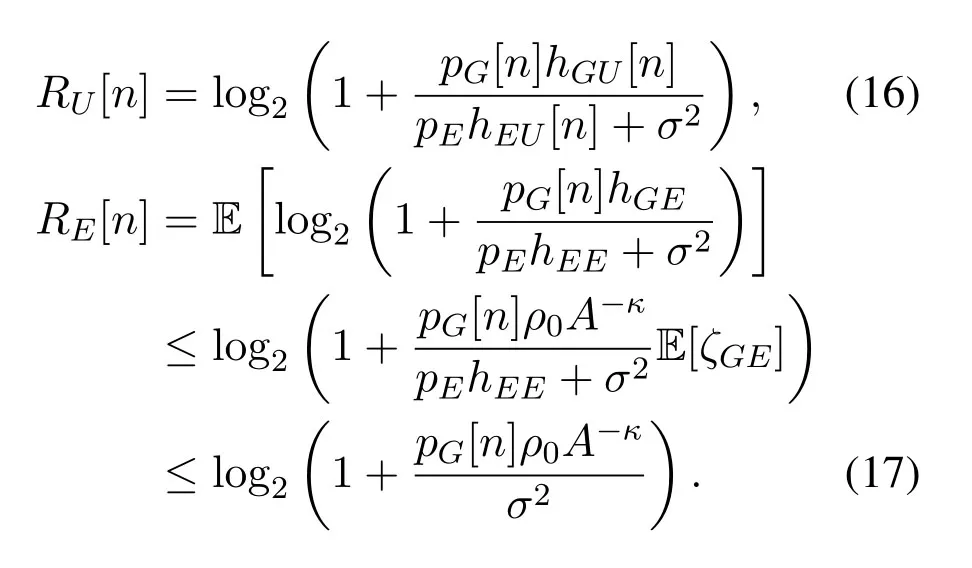
Eq.(17) holds due to the concavity ofRE[n]with respect toζGE[21]and the application of Jensen's inequality,as well as the assumption of perfect cancellation ofhEE.

2.2 Problem Formulation

For DL transmission,we aim to maximize the secrecy rate in(7)overNtime slots by jointly optimizing the UAV transmit power pU≜{pU[n],n ∈N}and the UAV trajectory q ≜{q[n],n ∈N}.Since the secrecy rate is non-negative in practice,RUTsecis at least zero when adaptively settingpU[n]=0 under the power constraint (6).As such,the operation []+can be dropped and thus the maximization problem is formulated as below

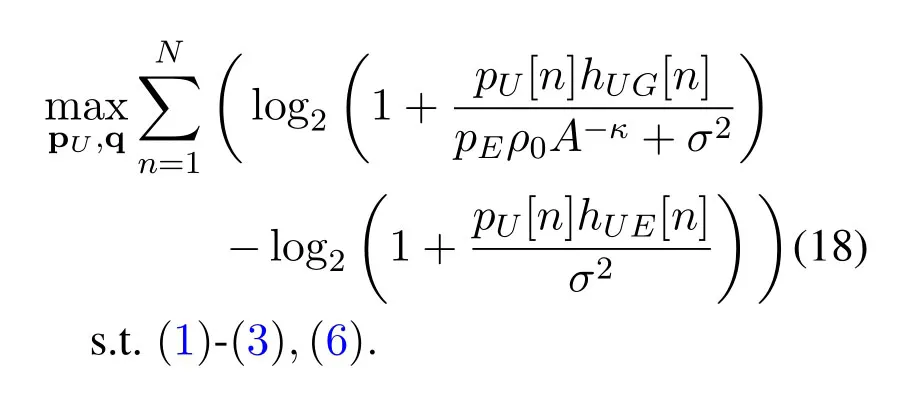
Similarly,for UL transmission,our goal is to maximize the secrecy rate in(15)by jointly optimizing the G's transmit power pG≜{pG[n],n ∈N}and the UAV trajectory q ≜{q[n],n ∈N}.As such,the maximization problem for the UL case is given by

In general,solving problems (18) and (19) optimally with feasible complexity are both challenging since their objective functions are not concave with respect to their respective optimization variables.In Section III and IV,we propose efficient iterative algorithms based on BCD and SCA methods to obtain suboptimal solutions to problems (18) and (19),respectively.

III.PROPOSED ALGORITHM FOR SOLVING PROBLEM(18)

In this section,we first consider problem(18)for DL transmission.Specifically,we cope with problem(18)by solving two subproblems iteratively,i.e.,the alternate optimization of the UAV transmit power pUand the UAV trajectory q.

3.1 Transmit Power Optimization Of the UAV

For given q,problem(18)can be rewritten as

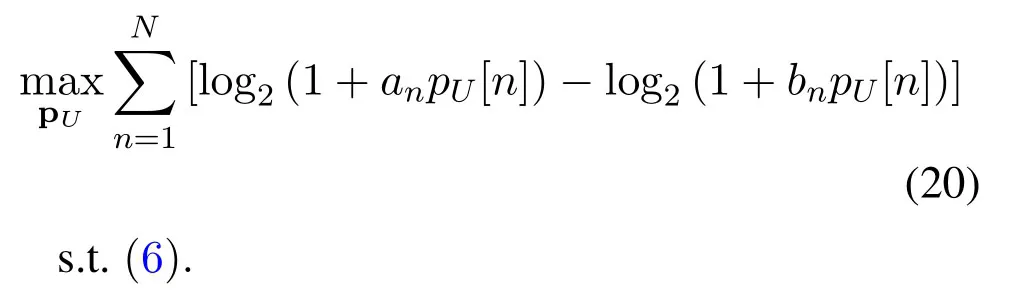
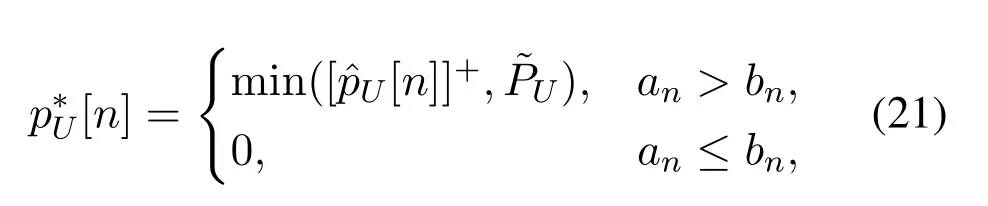
3.2 UAV Trajectory Optimization

With given pU,by letting l={l[n],n ∈N}and m={m[n],n ∈N}as the introduced slack variables,we can express problem(18)as

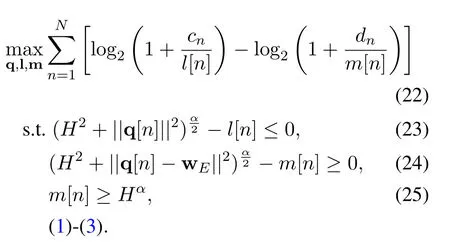
wherecn=γ0pU[n].

Note that the constraints (23) and (24) must hold with equalities in order to obtain the optimal solution,otherwisel[n](m[n]) can be increased (decreased) to decrease the objective value of problem (18).Therefore,problem(22)has the same optimal solution of q as that of problem(18).

Despite the introduction of slack variables,problem (22) is still non-convex due to its non-convex objective function and constraints.However,we observe that log2in (22) is convex with respect tol[n].As such,the SCA technique can be applied to solve problem (22) approximately.By using the first-order Taylor expansion at given local points denoted as lk=lk[n],n ∈Nin thek-th iteration,log2can be lower-bounded by

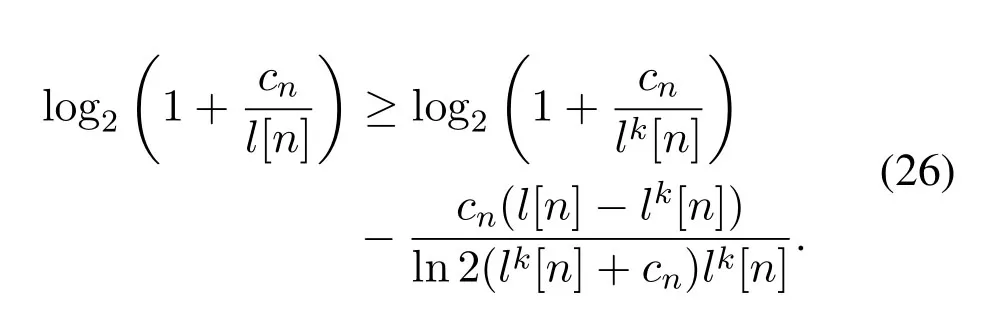
According to the conditions on guaranteeing the convexity or concavity of composition functions in[21],is convex with respect to q[n].Similarly,by using the first-order Taylor expansion at the given local points denoted as qk=qk[n],n ∈Nin thek-th iteration,we have

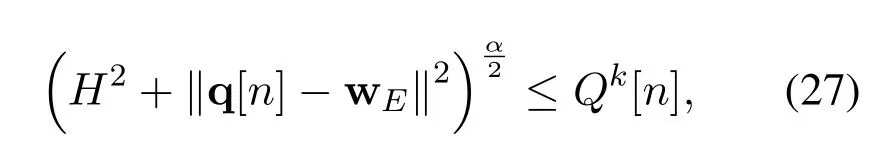
Hence,with (26) and (27),problem (22) can be lower-bounded by

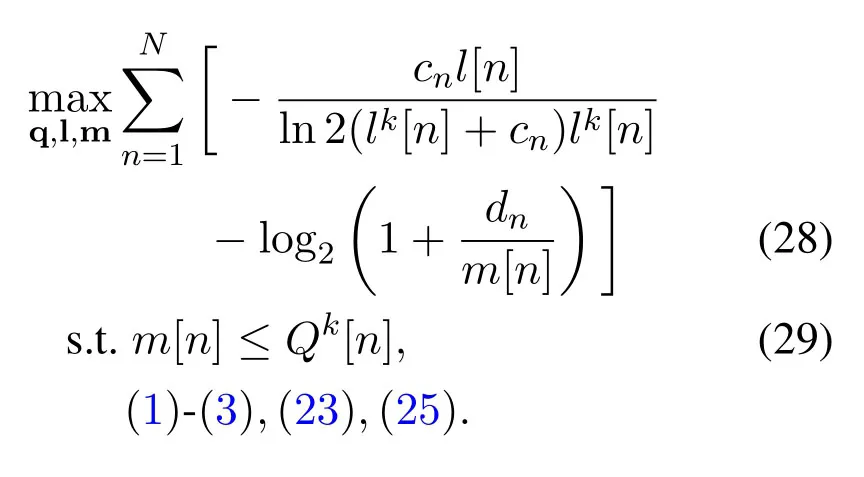
We can see that the objective function of problem(28)is concave with all convex constraints now.Thus,it can be efficiently solved by the commonly used CVX solver[22].

3.3 Overall Algorithm and Computational Complexity

To sum up,the overall algorithm can achieve a suboptimal solution to problem(18)by alternately optimizing variables pUand q in an iterative way.The detailed process for solving problem(18)is summarized in Algorithm 1.

?

Based on the analysis in [9],Algorithm 1 ensures that the obtained objective value of problem (18) is non-decreasing over the iterations.The total complexity of Algorithm 1 is given byO(KN3.5),whereKpresents the iteration number.

IV.PROPOSED ALGORITHM FOR SOLVING PROBLEM(19)

In this section,we consider the UL case.Similar to (18),we can also apply the BCD method to solve problem (19) by coping with two subproblems iteratively,i.e.,the alternate optimization of the G's transmit power pGunder the given UAV trajectory q as well as the UAV trajectory q under the given G's transmit power pG,until the algorithm converges.

4.1 Transmit Power Optimization Of G

For given UAV trajectory q,problem (19) can be rewritten as

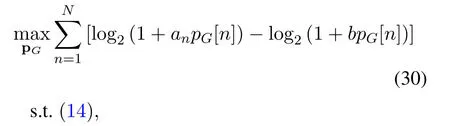
4.2 UAV Trajectory Optimization

With given pG,leten=γ0pG[n]andf=γ0pEfor notation simplicity.Similarly,we introduce slack variables l={l[n],n ∈N}and m={m[n],n ∈N}.Then,problem(19)can be reformulated as

Despite the reformulation of problem (19),the objective function of problem (31) is still non-concave with its optimization variables.However,the function log2is jointly convex with respect tom[n]andl[n].As such,by using Taylor expansion of a convex functiong(x,y) in a neighborhood of(x,y)=(x0,y0),i.e.,g(x,y)≈g(x0,y0)+gx(x0,y0)(x - x0) +gy(x0,y0)(y - y0).The term log2in problem (31) at given local points denoted byand mk=in thek-th iteration,can begiven by

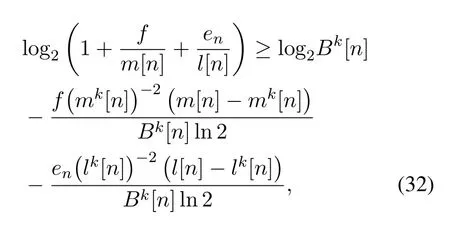
For the non-convex constraint (24),it can be handled similarly as(27)to obtain constraint(29).Therefore,problem(31)can be lower-bounded by

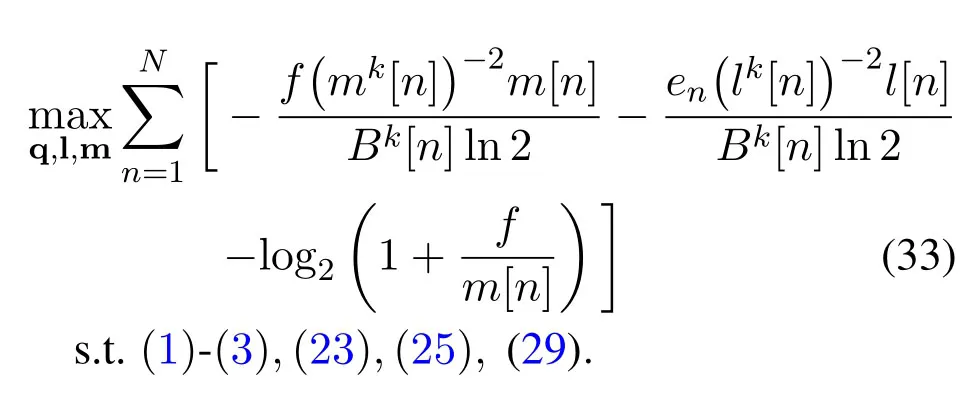
It is observed that problem (33) is convex with all convex constraints.As such,the CVX solver can also be used to efficiently solve this problem.Due to the similar algorithm with that for solving problem(18),we omit the details of the overall algorithm for UL transmission for brevity.Moreover,the complexity of the proposed algorithm is also in the order ofO(KN3.5),which means that the suboptimal solution is computed in polynomial time,and thus can be efficiently applied in practical systems.

V.NUMERICAL RESULTS

In this section,we show simulation results to verify the effectiveness of the proposed joint transmit power control and UAV trajectory optimization (denoted as T&P) algorithm for improving the secrecy rate performance.For comparison,two benchmark schemes are also considered in the following:1)UAV trajectory optimization without power control(denoted as T/NP);and 2) Heuristic UAV trajectory with power control (denoted as HT/P).Specifically,the UAV trajectories in T/NP are obtained by solving problems (28) and (33) iteratively until the corresponding algorithms converge,respectively,with equal transmit power allocation over the whole durationT,i.e.,pG[n]=¯PGandpU[n]=¯PU.For the HT/P scheme,the UAV first flies directly to the location right above G at its maximum speedVmax,then stays hovering as long as it can.By the end ofT,it returns to its final location atVmax.Given the fixed trajectories in HT/P,the transmit powerspU[n]andpG[n]for DL and UL transmissions can be obtained by solving problem (20) and (30),respectively.The simulation parameters are elaborated in Table1.

5.1 Downlink Transmission

We first testify the convergence of the proposed Algorithm 1 for the DL case in Figure2.It can be observed that the average secrecy rate increases with the number of iterations and rapidly converges after about 8 iterations for differentT.Moreover,with the increase ofT,the rate performance improved significantly.Note that no rate improvement can be observed forT=140s.The reason is that without sufficient flying time for the UAV to complete its mission,the UAV cannot enjoy the benefits of the flexible trajectory design.

Figure3 illustrates different UAV trajectories by different schemes for DL transmission with differentflight periodT.SinceT=140s is the shortest time for the UAV to fly from the initial location to the final location,the trajectories of all schemes are the same as a straight line.WhenT=145s,because the flight period is not enough for the UAV to reach G at its maximum speed,the UAV flies as close as possible to G and then arrives at the final location by the end of the limited duration.However,whenTis sufficiently large,e.g.,T=150s,it is observed that the UAV in T&P first flies to the left of G along an approximate straight line,compared with that in HT/P which flies directly towards G.This is because at its hovering location,the UAV in T&P can achieve an optimal balance between the information leakage to E and jamming from E minimization as well as the achievable rate maximization.During the return trip,it is expected that the UAV trajectory in T&P is farther away from E compared to that in HT/P due to the optimized trajectory that degrades the channel quality of the leaked UAV-to-E transmission.However,the UAV trajectory in T/NP flies along a larger curved path to complete its mission,which differs much compared with that of other schemes.The reason is that since there is no power control,the UAV has to adjust its trajectory to fly father away from E to prevent it from leaking more information to E.

Table1.Simulation parameters.

Figure2.Average secrecy rate versus iteration number.

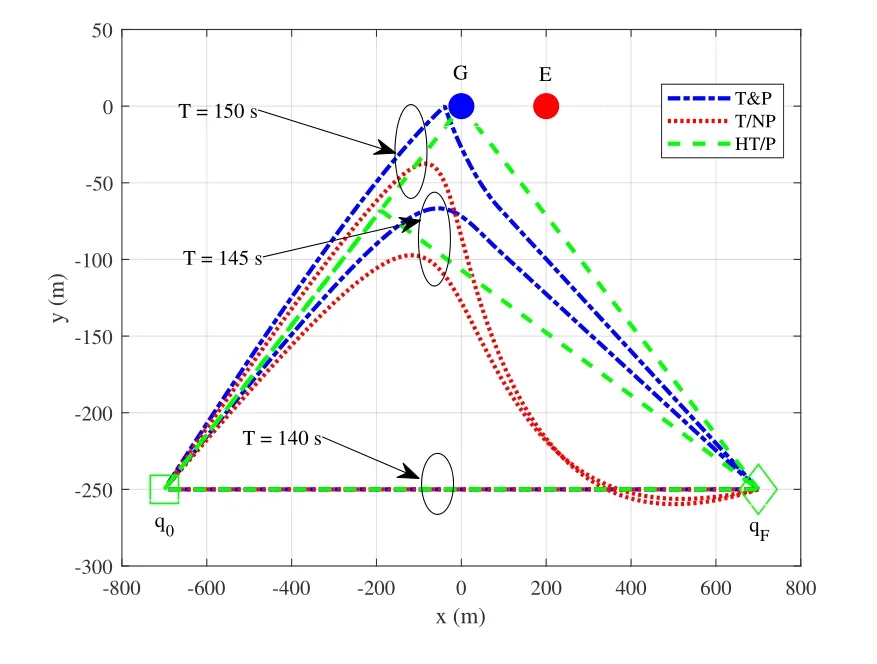
Figure3.UAV trajectories by different schemes for DL transmission.

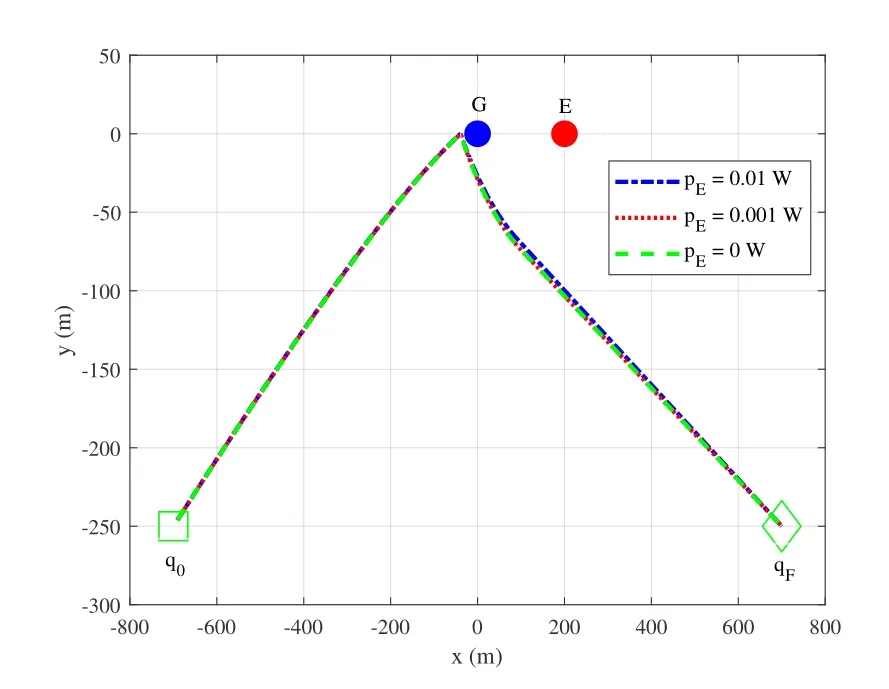
Figure4.UAV Trajectories by T&P under different jamming powers for DL transmission.

Figure4 shows different trajectories by T&P versus jamming powerpEfor DL transmission.As expected,all UAV trajectories are identical.This is because the interference generated by the active eavesdropper mainly affects G,but has no impact on the UAV.Therefore,in the case of DL transmission,different jamming powers induced by E do not lead to the change of the resulting UAV trajectory.

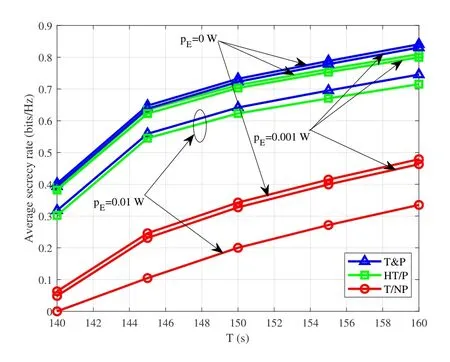
Figure5.Average secrecy rate versus T for DL transmission.

Figure5 illustrates the average secrecy rate versusTby different schemes with differentpE.It is shown that the average secrecy rates of all schemes increase withT.The reason is that the UAV can stay longer at its hovering location with the optimal trade-off whenTis sufficiently large,thus leading to the larger secrecy rates.By comparing with all schemes,we can see that the proposed T&P scheme has the best secrecy rate performance while the T/NP scheme achieves worst.Although the secrecy rates of all schemes reduce with the increase of the jamming powerpE,as expected,their gaps become larger withT,which demonstrates the importance of the proposed joint trajectory and power control design against active eavesdropping.Particularly,by comparing the gains between T&P and T/NP,the results indicate that the transmit power control of the UAV is more effective for improving the secrecy rate performance in DL transmission.

5.2 Uplink Transmission

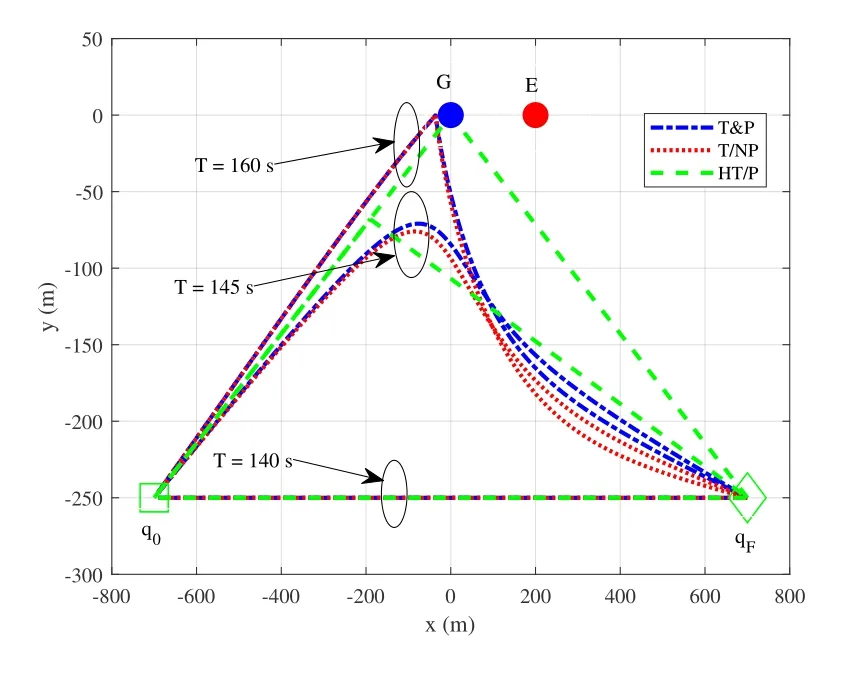
Figure6.UAV trajectories by different schemes for UL transmission.

Figure6 describes the UAV trajectories by different schemes in UL transmission with different flight periodT.It is shown that the UAV trajectories in T&P and T/NP are similar from q0to G but different in return trip with differentT.Particularly,whenTis sufficiently large,i.e.,T=160s,we can see that the UAV in T&P and T/NP flies to the left location of G at its maximum speed.At its hovering location,the UAV can arrive at an optimal trade-off to maximize the secrecy rate.However,when returning to its final location,the UAV in T/NP flies with a larger arc,compared to that in T&P.This is because without power control,the UAV in T/NP can only improve its secrecy rate via adjusting its trajectory to prevent it from the serious interference caused by E.

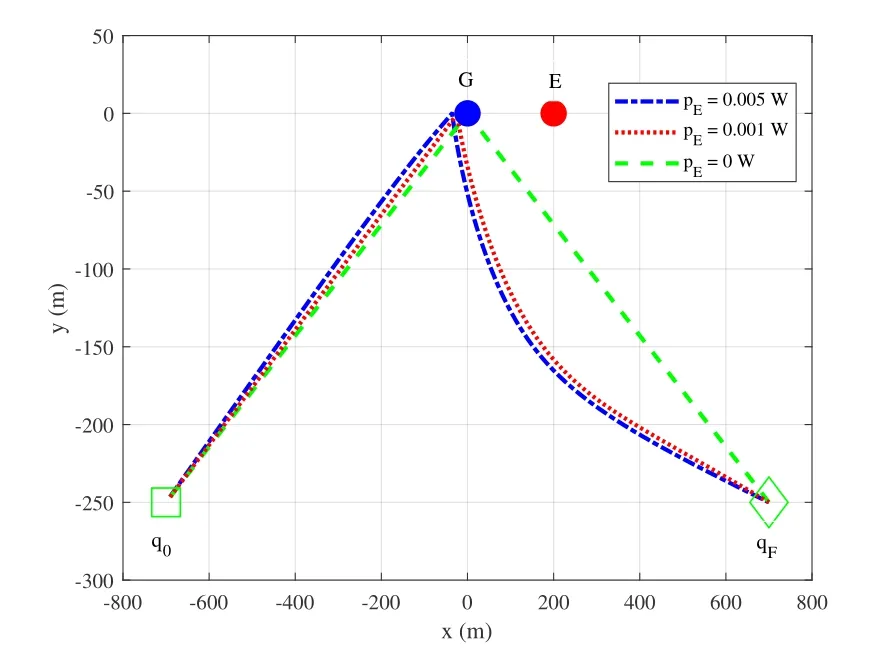
Figure7.UAV Trajectories by T&P under different jamming powers for UL transmission.

Figure7 illustrates the UAV trajectories by different jamming powers in UL transmission whenT=160s.It is observed that the hovering location of the UAV is farther from G when E transmits with higher jamming power.This is because in the UL case,jamming is more dominant in degrading the system performance.As such,the UAV needs to adjust its trajectory to strike a balance between maximizing the data collection rate while minimizing the malicious interference caused by E.Moreover,when the UAV returns to its final location,the UAV subjected to higher jamming power flies with a much larger arc.This indicates that the proposed scheme can effectively utilize the flexible UAV trajectory to prevent the active eavesdropping from the jamming and eavesdropping.Note that the UAV trajectory is same as that in the HT/P scheme whenpE=0W.The reason is that in this case,E only wiretaps the confidential information from G,without sending jamming signals to the UAV.As such,both the jamming and eavesdropping of E have no impact on the UAV trajectory.

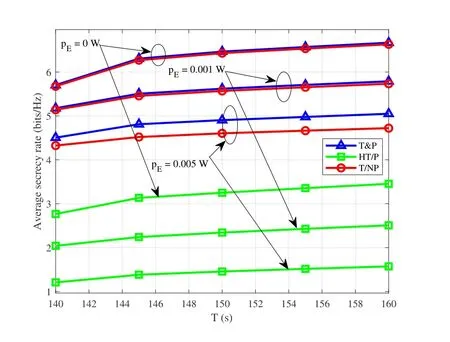
Figure8.Average secrecy rate versus T for UL transmission.

Figure8 shows the average secrecy rate versusTby different schemes with differentpE.It is observed that the average secrecy rate of the proposed T&P scheme outperforms other benchmark schemes,due to the joint optimization of the UAV trajectory and power control.Moreover,the secrecy rate gaps among all schemes become larger with the increase ofpE,which indicates the dominant role of the antiactive eavesdropping trajectory design.In particular,the larger gaps between T&P and HT/P for higher jamming power demonstrate that in the UL case,the UAV trajectory is more effective in improving secrecy rate performance,compared to the DL case.

VI.CONCLUSION

To tackle the new security challenges from active eavesdropping,in this paper,we studied secure UAV communication issues for both the UL and DL transmissions.We aimed to maximize the average achievable secrecy rates by jointly optimizing the G/UAV's transmit power control and UAV trajectory.To efficiently solve the non-convex optimization problems,we proposed iterative algorithms to cope with them based on BCD and SCA methods.Simulation results demonstrate that the proposed algorithms can improve the secrecy rate performance for both the DL and UL communications,by comparing with other benchmark schemes.Besides,it is shown that power control is more significant in improving the secrecy rate performance for DL transmission while the anti-active eavesdropping UAV trajectory design is more dominant for UL transmission.

Although we focus on securing UAV communications against active eavesdropping,the problem of secure transmission in UAV-assisted NOMA networks can also be solved by following a similar joint trajectory and power control optimization algorithm.In addition,it is interesting to pursue the application of the proposed scheme in urban areas.In this case,the angle-dependent Rician fading channel[23]or the probabilistic LoS channel[24]models can be adopted to design 3D UAV trajectory with both horizontal and altitude location optimization.

ACKNOWLEDGEMENT

This work was partially supported by the National Natural Science Foundation of China(No.61802034),National Key Research and Development Program of China(No.2019YFC1509602)and Chongqing Natural Science Foundation(cstc2019jcyj-msxmX0264).

NOTES

1Since we target for the offline UAV trajectory design,and E also transmits jamming signals besides passive eavesdropping,it can be located by jammer detection methods with high accuracy such as those in[25,26].Furthermore,even if E does not send jamming signals,but only passively eavesdrops,its location can be practically detected via a UAV-mounted camera or radar[27,28].

2Since field experiments demonstrate that the LoS probability of the UAV-to-ground channel approaches to 1 at high altitudes[29-31],we consider LoS channel model for practicality.