Application of a modified SAGAClA optimization algorithm in multimodal function optimization
Xiu-shuang CAO,Zhi-jun ZHANG,Shu-hui XU*,Rui-jia DONG,Guang-shuang MENG
(1Tangshan Polytechnic College,Tangshan 063299,China)
(2 Equipment Department,Shougang Jingtang United iron and Steel Co.,Ltd.,Tangshan 063299,China)
Abstract:Aiming at the problem that searches stepδ′parameter is invariable in the process of SAGACIA optimization algorithm,the improved adaptive step was presented,which made the step parameterδ′change adaptively in the process of optimization.And the modified adaptive SAGACIA optimization algorithm was used in optimizing multimodal function,which efficiently solved the partial search performance and the global convergence.The results of the applications showed that the modified SAGACIA optimization algorithm was practical and efficient.
Key words:SAGACIA optimization algorithm,Multimodal function,Adaptive stepδ′,Convergence property
1 Introduction
With the rapid development of science and technology,Optimization technology has been infiltrated into a variety of areas.Many practical application problems,such as engineering design,combinatorial optimization and decision support,have had multiple solutions.But all these practical problems can be attributed to the problem of searching function results after the mathematical modeling treatment.So,it is important that the study is applied to optimize function solution.
In recent years,many scholars have used different optimization algorithm to function optimization problem attempt.In references[1-2],the improvement in genetic algorithm from various aspects is presented,and it is used in optimizing multimodal function,which has achieved good results to a certain extent.After all,genetic algorithm requires coding and decode.which makes genetic algorithm discommodiously in use;In references[3],the modified particle swarm optimization algorithm is used to optimize function,which makes use of population diversity information to adjust inertia weight nonlinearly.This algorithm improved on solving function optimization problems to a certain extent;In references[4],the ant colony optimization is used to optimize function,which updates pheromone of the ant colony algorithm by the genetic algorithm encoding;Moreover,immune algorithm,frog-leaping algorithm and clonal selection algorithm are used to optimize function problems too.In this paper SAGACIA[5]optimization algorithm is modified,and used to optimize multimodal Function.This method is applied to both continuous optimizationand discrete optimization,and doesn’t need to encode and decode like genetic algorithm that influence on search ability and speed.The results of application is compared with genetic algorithm,which shows that the modified SAGACIA optimization algorithm is practical and efficient in optimizing function.
2 SAGACIA optimization algorithm
2.1 Frame and characteristic of SAGACIAoptimization
SAGACIA optimization is a kind of hybrid stochastic optimization algorithm,it integrates strongpoint of SAA,GA and CA;and improves efficiency of algorithm ulteriorly.In essence,this optimization algorithm adopts two sorts searching methods in the course of searching,named“assured”search and“eyeless”search.The foregoing makes search along with the direction whose result is more and more better in the course of search;Reversely,the latter accepts inferior result by a certain manner in the course of search.The foregoing can make algorithm converge to result that its capability is excellent;The latter can make algorithm escape from local minima.Both of search manners cooperate reciprocally,which makes sure that algorithm has good performances.
2.2 The primary step of SAGACIA optimization algorithm
Step 1Initialization
Produce n initial value(x0i)randomly and make x0ias new result(xi),x0i∈S,‘S’as the feasible gather,i=1,2,…,n,calculating relevant performance index(c(xi)),and making iterative variable as zero(k=0).
Step 2Carrying through search of‘R’type
Produce a group of new results(x′i)randomly near the every results of recent result gather,x′i∈S,calculate its relevant performance index(c(x′i)).IF c(x′i)≤c(xi),then accepting x′ias current result,namely xi=x′i,else also accept according to probability.
Step 3Carry through search of‘F’type
Make optimum result be saved as x*variable,and produce m new results(xj)randomly near theδ′range of x*,xj∈S(j=1,2,…,m),IF c(xj)≤c(x*)THEN x*=xj,ELSE throw away xj.
Step 4The mutation disturbance
Select some results randomly from current results by the mutation selective probability(Ps),and mutate by the mutation probability(Pm),substitute new result for primary result.
Step 5k=k+1,if the condition is satisfied to algorithm,then algorithm isterminated,else‘Step 2’.
3 The improvement of SAGACIA optimization algorithm—adaptive stepδ′
SAGACIA optimization is a kind of hybrid stochastic optimization algorithm.Similarly,some of the parameters is important in the course of optimization.In order to simplify program computing in standard algorithm,some parameters were fixed value.So the algorithm required extra time to search in the beginning and end of searching process,which influenced searching speed.The symbolδ′is the size of step for each search.The biggerδ′,the broader the scope in a certain time,but the rougher search too.On the contrary,the smallerδ′,the less the search scope and the more detailed the search process.The search stepδ′,both too big and too small,will influence on search efficiency[6].
In order to solve this contradiction,the mutativeδ′from big to small was adopted.In the initial stages of search process we chose the biggerδ′,which made the search process roughness.In the evening of search process,the rough area of optimum has been found basically.Here,we madeδ′small to strengthen fine search,so the optimum can be found accurately.
In order to makeδ′change adaptively in the course of optimization,the value ofδ′was achieved through the following formula(1).The value ofδ′is dropped off along with the increase of iterative time,the parameters including a and b can be achieved according to the actual problems and iteratives time.In this paper,the iteratives time is 25,by debugging,a=2,b=24.
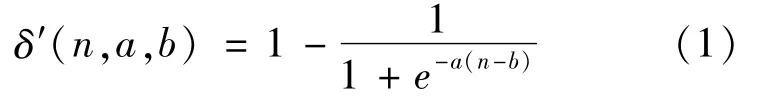
In this way,the value ofδ′change adaptively in optimization process,which improve the search speed.
4 Description of function optimization problem
For the actual optimization problem after dealingwith mathematical modeling,all can be boiled down to function optimization problems(most or least).In this paper,the most is discussed merely(least similarly).The function optimization problem can be described as following mathematical programming model[7],as following formula(2)shown:
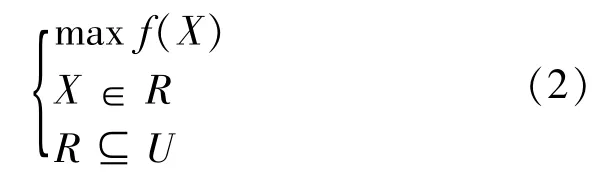
Where f(X)is the objective function,decision variable:X=[x1,x2,…,xn].The set R shows a result set that it consists of all results satisfying the constraint condition.U is basic solution space.Their relation is as shown in Fig.1.
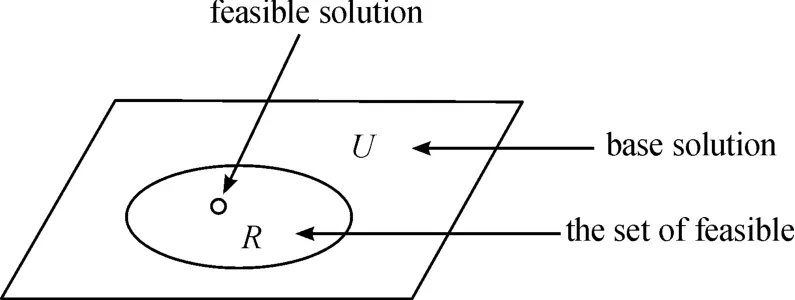
Fig.1 The feasible solution and its set of function optimization problems
In SAGACIA algorithm,one result of X=[x1,x2,…,xn](n-dimensional decision vector)set is a matrix of row n and one in the programming of Matlab.If a result set is m lists,m feasible solution participates in search process simultaneity.And determining the feasibility according to certain rules respectively searching,in the end the optimum of goal function decided is the optimum of function optimized.
Optimization problems of multimodal function exist in practice quantum similarly.It is an important aspect of function optimization.Multimodal function optimization is to search global optimal solution of goal function optimized domain space.When we search global optimum for multimodal function,the algorithm run into local optimum easily,and influence on optimization effect.
5 Test function and results
For the problem of complex functions optimization,it is imported that not only the fast convergence of the algorithm,but also it is more important to find the global optimal solution,avoid falling into local optimum.In order to verify the effectiveness of the improved SAGACIA algorithm,the following benchmark functions is selected as the test function:
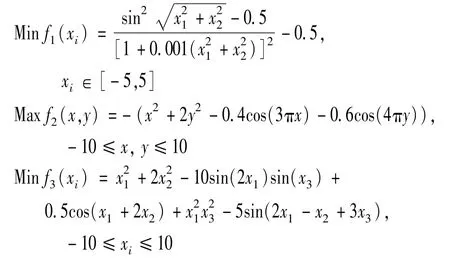
f1function is a multi-extreme value function with strong oscillation,which contains many local minima infinitely.The global optimal value is-1 at(0,0)point.Owing to the local optimal value around the global optimal value,-0.990 284 and-0.962 776.It is easy to fall into local optimum in the process of optimization.
f2function is a multimodal function,which contains many local maxima.But there is only one global maximum,the maximum value is 1 at(0,0)point.
f3function is a multi-extremum function with the characteristics of nonlinearity,asymmetry and inseparability.But there is only one global minimum at(-0.676 256,-0.381 582,-1.282 828 68),and the minimum value is-12.765 473.
For the above functions,the improved algorithm and the standard algorithm are used to optimize the test function,in which the population size is 100,the number of iterations is500.The neighborhood step size adopts the adaptive step size as formula(1).As the iteration goes on,the step size becomes smaller and smaller when it gets closer to the optimal solution.The selection and mutation probability in the standard algorithm is0.1 and 0.01.When the other parameters are the same,the optimization algorithm runs independently for 20 times.The comparison of the test results is shown in Table 1.
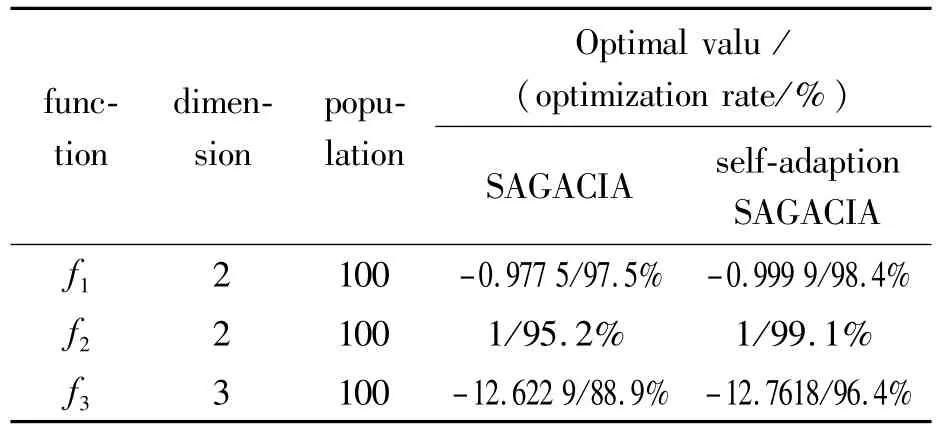
Table 1 The result of test function optimization
As shown as the test results,under the same condition for iteration numbers and populations,about f1function and f2function,the optimization accuracy and the optimization rate of the improved algorithm are improved to a certain extent.The optimum-0.999 9 is found at(-4.917 9,3.527 0)point about f1function.The improved optimization algorithm can find optimal value of 1 for both f1function and f2function.But the self-adaptive SAGACIA are improved in the optimization rate and convergence speed.The optimum-12.761 8 is found at(-0.673 9,-0.344 9,-1.279 1)point about f3function through the selfadaptive SAGACIA algorithm.And,the optimum-12.622 9 is found at(-2.813 8,-2.327 9,-2.483 9)through the standard SAGACIA algorithm.Before and after the improvement of the algorithm,the optimization curve of the test function is shown in Figs.2-4.
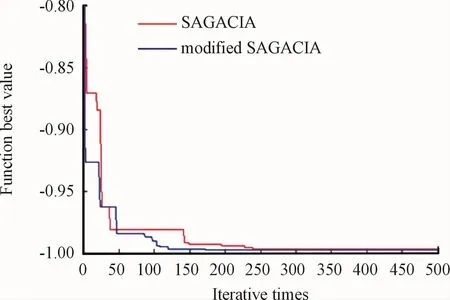
Fig.2 The optimization curve of f1 function
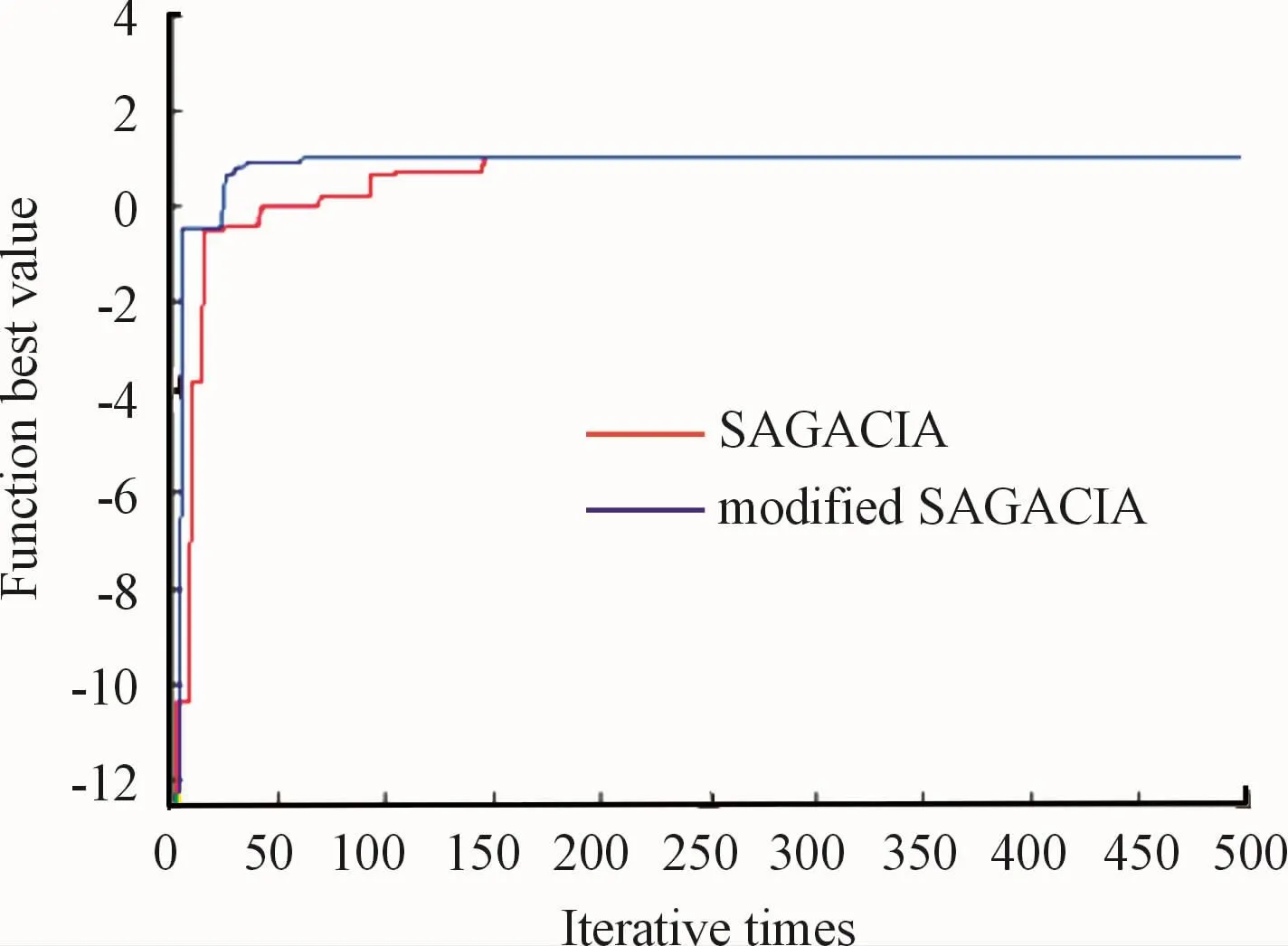
Fig.3 The optimization curve of f2 function
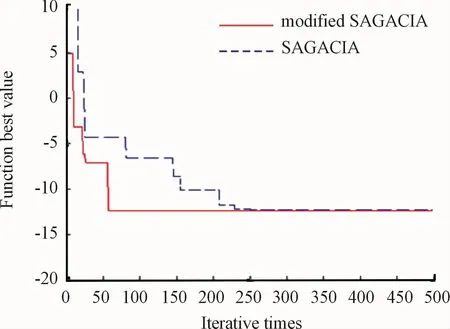
Fig.4 The optimization curve of f3 function
6 Conclusions
SAGACIA optimization is a kind of hybrid stochastic optimization algorithm.The control parameters influence on the algorithm performance importantly.In standard SAGACIA algorithm,the search stepδ′parameter is unchanged in the course of search,which influences efficiency of search.In this paper,δ′parameter is variational adaptively.As a result,the search performance and speed are improved.
Aiming at falling into local optimum easily and slow convergence later stage in optimizing complex function by SAGACIA,modified SAGACIA optimization algorithm using adaptive step is proposed,which improves global and local search capability of algorithm.Simulation test shows that the algorithm is improved in search speed and search accuracy.Therefore,the improvement of algorithm is effective and feasible.But because the parameters in algorithm are set through many experiments,the optimization of algorithm parameters and other application need to study further,which is also next job.
- 机床与液压的其它文章
- Lubricating performance of conical spindle distribution in the ball piston pump
- Mechanism analysis and control of asymmetrical digital cylinder
- Reliability analysis and calculationof the drive hydraulic system group of combined transportation
- Reliability analysis for cutterhead hydraulic drive system of remanufactured shield machine
- Application of compound buffer hydraulic cylinder in electro-hydraulic load simulator(EHLS)
- Start-up characteristics of a new electro hydrostatic actuator with an accumulator

