Normalized bidirectional projection-based multiple attribute group decision making method with crisp and interval information
Ju-feng YE
(Zhejiang Tongji Vocational College of Science and Technology,Xiaoshan 311231,China)
Abstract:Projection measure is a very suitable tool for dealing with multiple attribute decision making problems.It considers not only the distance but also the included angle between objects evaluated.However,the existing projection formulae are illogical in some cases.To overcome the shortcoming implied in the existing projection measures,this paper developed normalized bidirectional projection method,measuring real vectors and interval numbers and their multiple attribute group decision making method with the hybrid information of crisp values and interval numbers.Through the normalized bidirectional projection measure between each alternative decision matrix and the ideal alternative matrix,all alternatives can be ranked to determine the best matrix.An illustrative example,applied alternative selection in the flexible manufacturing system,demonstrates the effectiveness and advantages of the proposed method through a comparative analysis with the existing projection measures.
Key words:Normalized bidirectional projection measure,Group decision making,Interval number,Hybrid information
1 Introduction
Projection measure is a very suitable tool for dealing with decision making problems because it can consider not only the distance but also the included angle between objects evaluated[1-2].Therefore,may researchers have applied projection methods successfully to decision making.For example,Xu and Da[1]and Xu[2]developed two projection methods for uncertain multiple attribute decision making with preference information.Then,Xu and Hu[3]proposed the projection model-based approaches for intuitionistic fuzzy multiple attribute decision making.Zheng et al.[4]and Fu et al.[5]proposed grey relational projection methods with crisp values and applied them to multiple attribute decision making.Xu and Cai[6]presented projection model-based approaches for intuitionistic fuzzy multiple attribute decision making.Xu and Liu[7]put forward a group decision making approach based on interval multiplicative and fuzzy preference relations by using projection.Zeng et al.[8]presented a projection method for multiple attribute group decision making with intuitionistic fuzzy information.Yue[9-10]developed group decision-making methods based on projection measures with intuitionistic fuzzy information.Ju and Wang[11]proposed a projection method for group decision making problems with in-complete weight information in linguistic setting.Yue and Jia[12]introduced a group decision making method based on a projection measure with hybrid intuitionistic fuzzy information.
However,the author finds that the existing projection formulae are illogical(see Examples 1 and 3 in Section 3)in some cases and need to be improved to overcome the shortcomings implied in the existing projection measures.In order to do so,the main purpose of this paper is to develop normalized bidirectional projection measures of crisp values and interval numbers and their multiple attribute group decision making method with the hybrid information of crisp values and interval numbers.
The rest of the paper is organized as follows.Section 2 briefly describes the projection measures of real vectors and interval numbers.Section 3 proposes the normalized bidirectional projection measures of real vectors and interval numbers to overcome some shortcomings implied in the existing projection measures.In Section 4,we develop a multiple attribute group decision making method with the hybrid information of crisp values and interval numbers by using the normalized bidirectional projection measures.In Section 5,an illustrative example is presented to demonstrate the application of the proposed method,and then the effectiveness and advantages of the proposed method are demonstrated by a comparative analysis with the existing projection methods.Finally,Section 6 contains conclusions and future work.
2 Projection measures of real vectors and interval numbers
This section briefly describes the basic concepts of the projection measures of real vectors and interval numbers.
Definition 1[1-2].Let A=(a1,a2,…,an)and B=(b1,b2,…,bn)be two real vectors,then the cosine of the included angle between A and B is defined by
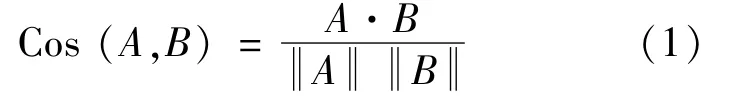
where the modules of the real vectors A and B areand the inner product between A and B is A·.
Definition 2[1-2].Let A=(a1,a2,…,an)and B=(b1,b2,…,bn)be two real vectors.Then,the projection of the vector A on the vector B is defined by

The projection measure ProjB(A)can include both the distance and the included angle between A and B.
In general,the bigger the value of ProjB(A)is,the closer A is to B[1-2].However,this case is not always reasonable in some case[7].For example,let A=B and C=2B,then.Clearly,ProjB(C)is larger than ProjB(A).In fact,A is closer to B than C.Hence,the projection cannot accurately depict the degree of vector A close to B.To overcome the shortcoming,the projection method was improved by Xu and Liu[7].
Definition 3[7].Let A=(a1,a2,…,an)and B=(b1,b2,…,bn)be two real vectors,then the projection of the vector A on the vector B is defined by
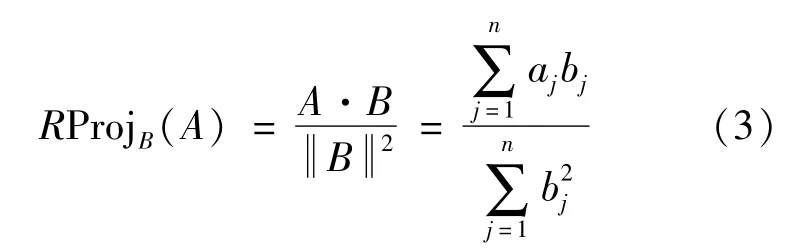
Which is also called the relative projection of the vector A on B.Thus,the closer the value of RProjB(A)is to 1,the closer the vector A is to the vector B.
Kaufmann and Gupta[13]introduced an interval number and defined as follows.
Definition 4[13].If a=[al,au]={x|al≤x≤au,al,au∈R},then a is called an interval number.If a=[al,au]={x|0<al≤x≤au},then a is called a positive interval number.If al=au,then a is reduced to a real number(crisp value).
In this paper,all interval numbers are considered to be positive.
If an interval number is considered as a two-dimensional vector,Xu[2]gave the projection measure between interval numbers as follows.
Definition 5[2].Let a=[al,au]and b=[bl,bu]be two interval numbers,then the projection of interval number a on b is defined as
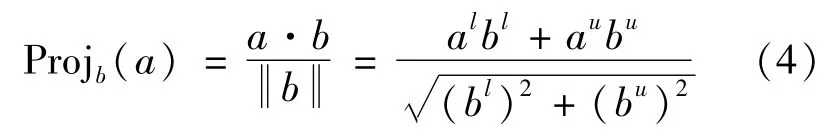
In general,the larger the value of Projb(a)is,the closer a is to b.
Similarly,since the projection measure implies some flaw,Xu and Liu[7]improved the projection measure and gave the following definition.
Definition 6[7].Let a=[al,au]and b=[bl,bu]be two interval numbers,then the projection of interval number a on b is defined as

Similarly,the closer the value of Projb(a)is to 1,the closer the interval number a is to b.
However,the“closeness”between two vectors for the projection measures introduced by Xu and Liu[7]is not also always reasonable in some cases,which are discussed in the following section.
3 Normalized bidirectional projection measures of real vectors and interval numbers
Although Xu and Liu[7]improved the projection measures of real vectors and interval numbers,these projection measures are not also always reasonable in some cases.Therefore,this section proposes normalized bidirectional projection measures between real vectors and between interval numbers to overcome the shortcomings implied in the existing projection measures.
Firstly,the following example is given to indicate some shortcomings of the existing projection measures between real vectors.
Example1.Let us take two real vectors A=(1,1)and B=(1,0).According to Eqs.(2)and(3),there are ProjB(A)=ProjB(B)=1 and R ProjB(A)=R ProjB(B)=1.In the cases,it is obvious that B is much closer to itself rather than to A since A≠B and the module of A is more than that of B.Therefore,the projection measures of the“closeness”between two vectors are unreasonable in the cases.
Then,the author notices that when A is equal to B,ProjB(A)should be equal to 1,conversely ProjA(B)should be also equal to 1.Hence,the author proposes normalized bidirectional projection measures between two real vectors below.
Definition 7.Let A=(a1,a2,…,an)and B=(b1,b2,…,bn)be two real vectors,then the normalized bidirectional projection measures between two vectors A and B are defined,respectively,as follows:

Where the modules of the real vectors A and B areand the inner product between A and B is A·It is obvious that if and only if A is equal to B,B Projs(A,B)(s=1,2)is equal to 1 to indicate the“closeness”between the two vectors.Obviously,there are 0≤B Proj1(A,B),B Proj2(A,B)≤1 for any two vectors A and B,which are the normalized measures.
To demonstrate the rationality and effectiveness of the normalized bidirectional projection measures,we give the following example.
Example 2.Let us reconsider Example 1.According to Eqs.(6)and(7),there are A·B=1,thus,BProj1(A,B)=BProj2(A,B)=1/(1+1-1/2)=0.666 7.
It is obvious that the results of the normalized bidirectional projection measures are reasonable since A≠B and B Projs(A,B)=1 for s=1,2 if and only if A=B.
On the other hand,the following example is provided to indicate some shortcomings of the existing projection measures between interval numbers.
Example 3.Suppose that there are two interval numbers a=[1,2]and b=[0,2].There are Projb(a)=Projb(b)=4/2=2,2.236 1 and R Projb(a)=R Proja(a)=R Projb(b)=1 according to Eqs.(4)and(5).In the cases,it is obvious that these projection measures are not reasonable since the module of a is more than that of b and a≠b
Similarly,if we consider an interval number as a two-dimensional vector,the author proposes the following normalized bidirectional projection measures between interval numbers to overcome the shortcomings implied in the existing projection measures.
Definition 8.Let a=[al,au]and b=[bl,bu]be two interval numbers,then the bidirectional projection measures between interval numbers a and b are defined,respectively,as follows:
Obviously,there are 0≤ B Proj1(a,b),B Proj2(a,b)≤ 1 for any two interval numbers a and b,which are the normalized measures.
The following example is presented to demonstrate the rationality and effectiveness of the normalized bidirectional projection measures between interval numbers.
Example 4.Let us reconsider Example 3.According to Eqs.(8)and(9),the following results can be obtained,respectively,as follows:

Clearly,the results of the two normalized bidirectional projection measures are reasonable since a≠b and B Projs(a,b)=1 for s=1,2 if and only if a=b.
Definition 9.Let X=(xkj)t×nand Y=(ykj)t×nbe two matrices,where xkj=(k=1,2,…,t;j=1,2,…,n).Then the normalized bidirectional projection measures between X and Y are defined,respectively,as follows:
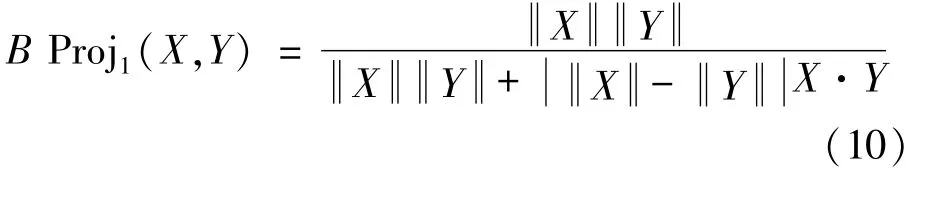


Then,by using Eqs(10)and(11),we have the following normalized bidirectional projection measure results,respectively,as follows:
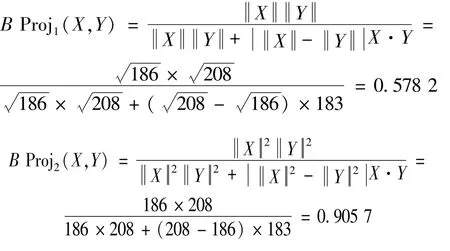
4 Group decision method based on the normalized bidirectional projection measures
This section develops a multiple attribute group decision making method by using the normalized bidirectional projection measures with crisp and interval information.
Since the hybrid information of crisp values and interval numbers can be represented by interval information,we only consider a multiple attribute group decision making problem with interval numbers.let A={A1,A2,…,Am}be a discrete set of alternatives,G={g1,g2,…,gn}be a set of attributes,and D={d1,d2,…,dt}be a set of decision makers.Then,assume that the weight vector of attributes given by decision makers is W=(w1,w2,…,wn)Twith wj≤ 0 andand the weight vector of decision makers is V=(v1,v2,…,vt)Twith vk≤ 0 and1.If each decision maker dk(k=1,2,…,t)provides an evaluation value of the alternative Ai(i=1,2,…,m)with respect to the attribute gj(j=1,2,…,n)by using a scale(e.g.from 1(less fit)to 10(more fit)),each attribute value can be characterized by an interval number2,…,n;i=1,2,…,m).Thus,we can elicit the group decision matrix of each alternative Xi=is provided by the decision maker dk(k=1,2,…,t).In the following statements,Xiis called the alternative decision matrix for short.Thus,the steps of the group decision making problem are described as follows:
Step 1:By(k=1,2,…,t;j=1,2,…,n;i=1,2,…,m)according to the alternative decision matrix Xi(i=1,2,…,m),the weighted alternative decision matrix is obtained as Ri=)t×n.
Step 2:For all the weighted alternative decision matrices of Ri,the ideal alternative matrix R*=is determined by.
Step 3:According to Eq.(10)or Eq.(11),the normalized bidirectional projection measure between each weighted alternative decision matrix Ri(i=1,2,…,m)and the ideal alternative matrix R*can be calculated by

Step 4:The alternatives are ranked in a descending order according to the values of B Projs(Ri,R*)for s=1 or 2 and i=1,2,…,m.The greater value of B Projs(Ri,R*)means the better alternative Ai.
Step 5:End.
5 Example analysis
In this section,an illustrative example for multiple attribute group decision making problems with hybrid information of crisp values and interval numbers is provided to demonstrate the applications and effectiveness of the proposed decision making method in realistic scenarios.
5.1 Illustrative example
Let us consider a multiple attribute group decision making problem above alternative selection in the flexible manufacturing system.Assume that a set of four alternatives for the flexible manufacturing system is A={A1,A2,A3,A4}.We must take a decision according to the three attributes:(1)g1is the improvement in quality;(2)g2is the market response;(3)g3is the manufacturing cost.The four possible alternatives under the three attributes are to be evaluated by three decision makers corresponding to hybrid evaluation information of crisp values and interval numbers.Assume the weight vector of the three attributes is W=(0.38,0.3,0.32)Tand the weight vector of the three decision makers is V=(0.36,0.38,0.26)T.
Then,the three decision makers are invited to make judgments and to give the hybrid evaluation information of crisp values or interval numbers according to a scale from 1(less fit)to 10(more fit).Hence,the evaluation values of an alternative Ai(i=1,2,3,4)on an attribute gj(j=1,2,3)are given from the three decision makers,which are shown in the following four alternative decision matrices,respectively:

Then,the developed approach is used for ranking the alternatives and selecting the most desirable one(s),which can be described as the following steps:
Step 1:By calculating(k=1,2,…,t;j=1,2,…,n;i=1,2,…,m)according to the alternative decision matrix Xi(i=1,2,…,m),the four weighted alternative decision matrices are obtained,respectively,as follows:

Step 2:For all the weighted alternative decision matrices of Ri(i=1,2,3,4),the ideal alternative matrix is obtained byas follows:

Step 3:According to Eq.(12)or Eq.(13),the normalized bidirectional projection measure values between each weighted alternative decision matrix Ri(i=1,2,3,4)and the ideal alternative matrix R*can be obtained as follows:
B Proj1(R1,R*)=0.565 3,B Proj1(R2,R*)=0.631 7,B Proj1(R3,R*)=0.693 4,and B Proj1(R4,R*)=0.845 2;
or B Proj2(R1,R*)=0.794 3,B Proj2(R2,R*)=0.838 3,B Proj2(R3,R*)=0.873 7,and B Proj2(R4,R*)=0.938 2.
Step 4:Since the values of the two normalized bidirectional projection measures are B Proj1(R4,R*)>B Proj1(R3,R*)>B Proj1(R2,R*)>B Proj1(R1,R*)or B Proj2(R4,R*)>B Proj2(R3,R*)>B Proj2(R2,R*)>B Proj2(R1,R*)respectively,the two ranking orders of the four alternatives are identical and A4>A3>A2>A1.Hence,the alternative A4is the best choice among all the alternatives.
5.2 Comparison with other projection measures
In this subsection,we show a comparative analysis with the existing projection measures to illustrate effectiveness and advantages of the developed method.
For the above-mentioned example,if Eqs.(12)and(13)are replaced by the existing projectionmeasures:
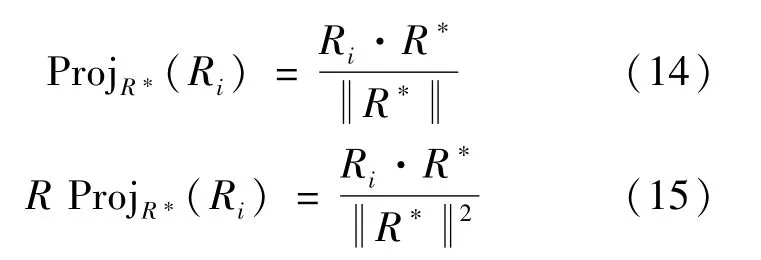
Then,the projections of Ri(i=1,2,3,4)on the ideal decision R*can be calculated by Step 3 and using Eqs.(14)and(15).Their results are shown as follows:
ProjR*(R1)=5.557 7,ProjR*(R2)=5.754 3,ProjR*(R3)=5.890 8,and ProjR*(R4)=6.130 6;R ProjR*(R1)=0.875 3,R ProjR*(R2)=0.906 3,R ProjR*(R3)=0.927 8,and R ProjR*(R4)=0.965 5.
Since the values of the two projection measures are ProjR*(R4)>ProR*(R3)>ProjR*(R2)>ProjR*(R1)and R ProjR*(R4)>R ProjR*(R3)>R ProjR*(R2)>R ProjR*(R1)respectively,the two ranking orders of the four alternatives is also identical and A4>A3>A2>A1.Hence,the alternative A4is also the best choice among all the alternatives.
Obviously,all ranking orders are identical by using various projection methods.Compared with the existing projection measures[2,7],the proposed normalized bidirectional projection measures are better than the existing projection measures because the normalized bidirectional projection measures can consider not only the distance and included angle between objects evaluated but also the bidirectional projection magnitudes,while the existing projection measures only consider the single directional projection magnitude between objects evaluated rather than the bidirectional projection magnitudes and implies some unreasonable phenomena in some case.As mentioned above,the normalized bidirectional projection measures can overcome the disadvantages of the general projection measures.
The main highlights of the proposed method are outlined as follows:
1)The normalized bidirectional projection measures are more reasonable than the existing projection measures because the former can overcome the shortcomings of the existing projection measures,then their measure values are bounded within[0,1],which are normalized measures.
2)The normalized bidirectional projection measures are more comprehensive than the existing projec-tion measures because the normalized bidirectional projection measures can consider not only the distance and the included angle between objects evaluated but also the bidirectional projection magnitudes.
3)The normalized bidirectional projection-based multiple attribute group decision making method with hybrid information is simple and effective,so it can be implemented easily on a computer.
6 Conclusion
This paper developed a normalized bidirectional projection method to overcome the shortcomings of the existing projection measures and their multiple attribute group decision making method,by considering hybrid information of crisp values and interval numbers.Through measuring the normalized bidirectional projection of each alternative decision matrix and the ideal alternative matrix,the ranking order of all alternatives were determined and the best alternative can be identified.To illustrate this,an example applying the developed method was given to demonstrate the effectiveness and advantages by a comparative analysis with the existing projection measures.
In the future work,we shall extend the normalized bidirectional projection measures to other decision information,such as intuitionistic fuzzy information and linguistic information,and develop their applications,such as decision making,pattern recognition,and medical diagnosis.
- 机床与液压的其它文章
- Lubricating performance of conical spindle distribution in the ball piston pump
- Mechanism analysis and control of asymmetrical digital cylinder
- Reliability analysis and calculationof the drive hydraulic system group of combined transportation
- Reliability analysis for cutterhead hydraulic drive system of remanufactured shield machine
- Application of compound buffer hydraulic cylinder in electro-hydraulic load simulator(EHLS)
- Start-up characteristics of a new electro hydrostatic actuator with an accumulator

