Augmented Lyapunov function-based finite-time control of networked system with structural uncertainty and jamming attack

Li-min WANG，He-jun YAO，Qian-tai YAN，Shuang Zhang，Kang Zhu

（Anyang Normal University，School of Mathematics and Statistics，Anyang 455000，China）

Abstract：In this paper，we consider the finite-time control problem of networked system with structural uncertainty and jamming attack.By constructing a new augmented Lyapunov function，the sufficient condition for the finite time stability of the system is explored.By involving linear matrix inequality approach，the sufficient condition is reduced to a feasibility problem which is dependent on network induced delay and the bound of external disturbance.Then，the design strategy of state feedback controller is proposed，which makes the network system more suitable for engineering practice.A numerical example is presented to illustrate the effectiveness of the proposed method.

Key words：Finite-time control，Induced Delays，State feedback，Networked system

Feedback control systems wherein the control loops are closed through a real-time network are called networked control systems（NCSs）［1-2］.The main feature of NCSs is that the components（sensors，controller and actuators）of the systems are connected by a network.Compared with traditional point-to-point control systems，the NCSs have many advantages such as low cost，reduced wiring，simple installation and maintenance，and high reliability［3-5］.Since Walsh put forward the concept of“networked control systems”in 1999，it has been well received by most scholars and has been used to this day.IEEE Transactions published special issues on network system research in 2001，2004 and 2007.In addition，IEEE transaction on automatic control，automatica and other famous journals in the field of automatic control published a lot of research results on network system［6-9］.Most of the research focuses on network induced delay，time-varying transmission period，packet disorder and loss，network scheduling，clock synchronization，network bandwidth limitation and so on.

In addition，the current results mainly focus on the asymptotic stability and focus on the steady-state performance of the system，while the research on the transient performance of the system is less［10-11］.In practical engineering，because the work time of the network system is generally short，people are interested in the asymptotic stability of the system，and they are more concerned about the transient performance of the system［12-13］.Therefore，the finite time performance analysis and control synthesis of the network system is particularly important.

In order to study the transient performance of power system，the concept of short-time stability，i.e.the concept of finite time stability，was first proposed in［14］，and the sufficient conditions for the existence of solutions of the problem were given by using Lyapunov function method.Then the linear matrix inequality theory is introduced into the finite time stability analysis and control design of linear systems［15］.The finite time stability of discrete time-varying linear systems is studied［16］.The necessary and sufficient conditions are given，and the problem of output feedback controller design is further studied.The finite time boundedness and dissipation analysis of a class of cascade networked control systems are studied［17］.Tuan et al.studied the finite time control problem of linear discrete time-delay systems.The problem of finite time stability of interval time-varying delay systems is solved by using linear matrix inequality（LMI）method.The sufficient conditions of finite time stability under norm bounded disturbance are obtained［18］.In China，Guan Xinping，Wu Yuqiang，Shen Yanjun，Li Shihua，Ding Shihong，Liu Fei，Hong Yiguang，sun Jiabing，Feng June and others have conducted in-depth research on the finite time control problem.For example，the finite time control problem for a class of linear discrete-time systems with time-varying，finite energy external disturbances is studied［19］.The sufficient conditions for solvability of the problem are given in the form of linear matrix inequalities.Wu Yuqiang et al.studied the input saturation finite time stabilization of uncertain nonholonomic systems［20］.But the above papers consider the Lyapunov stability for NCSs，a few results on finite-time stability for NCSs has been reported.Based on this fact，some new methods and approaches should be developed for design controllers of NCSs，which motivates this paper.Inspired by the above literature，in this paper，the attention is focused on the finite-time control of a class of NCSs with communication delay.The main result provided is a sufficient condition for the design of a state feedback controller which makes the closed loop systems finite-time stable.

1 Problem formulation

Consider the following typical networked system with structural uncertainty and jamming attack shown in Fig.1.

where A∈Rn×n，B∈Rn×m，B1∈Rn×lare constant matrices，x（t）∈Rnis the state vector，u（t）∈Rmis the control input.ω（t）∈Rlis the exogenous disturbance satisfying

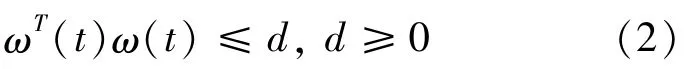
ΔA（t）∈Rn×n，ΔB（t）∈Rn×mare unknown matrices representing structural uncertainty satisfying

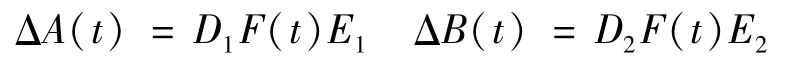
where D1，D2，E1，E2are known constant matrices，and F（t）is a time varying matrix

Fig.1 A typical networked control system

In Fig.1，τscandτcaare the sensor-controller and controller-actuator delay respectively，then the communication delay is given byτ＝τsc＋τca.Therefore，the system（1）can be rewritten as

In this paper，we will design a state feedback controller for the system（3）

where K is a constant matrix to be determined later.The closed-loop system can be obtained

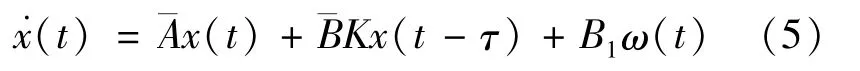
where

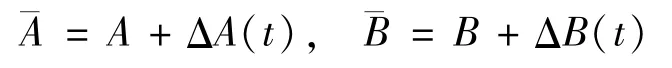
Definition 1Given three positive scalars c1，c2，T，with c1＜c2and a positive matrix R，the system（3）（settingω（t）≡0）is said to be finite-time stable with respect to（c1，c2，T，R），if

Lemma 1［3］For known constantε＞0 and matrices D，E，F which satisfying FTF≤I，then the following matrix inequality is hold

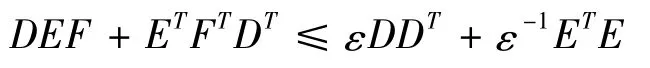
Lemma2［5］The linear matrix inequality

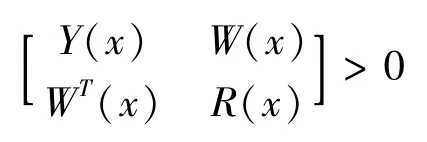
is equivalent to

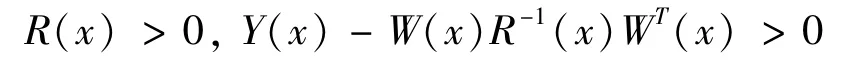
where Y（x）＝YT（x），R（x）＝RT（x）and W（x）depend on x.

2 Main results

2.1 The nonlinear sufficient condition of the finite-time stability

Theorem1.Given three positive scalars c1，c2，T，with c1＜c2，a positive definite matrix R，the system（3）is finite-time stabile via state feedback with respect to（c1，c2，T，R，d），if there exist a scalarα≥0，positive definite matrices P∈Rn×n，Q∈Rn×n，S∈Rl×l，and matrix K∈Rm×nsuch that the following matrix inequalities hold

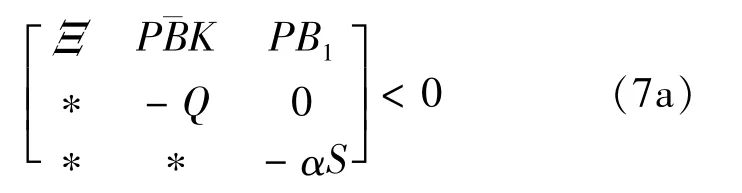
and

where

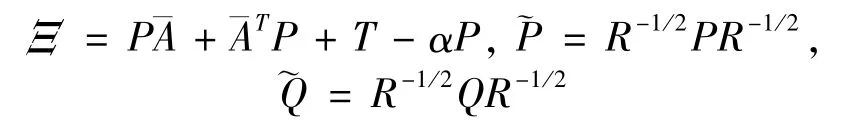
andλmax（）andλmin（）indicate the maximum and minimum eigenvalue of the augment，respectively.

Proof.Constructing an augmented Lyapunov function as

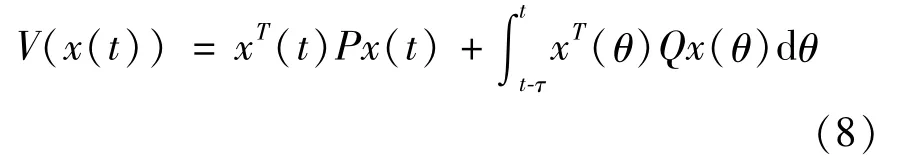
with the solution of the equation（5），it is easy to obtain

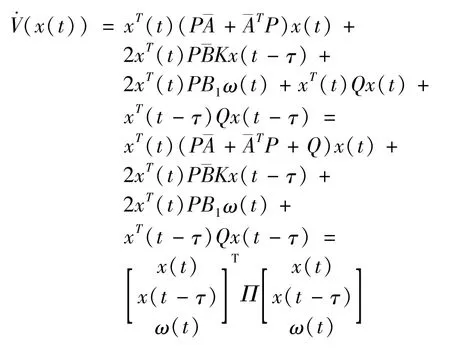
where

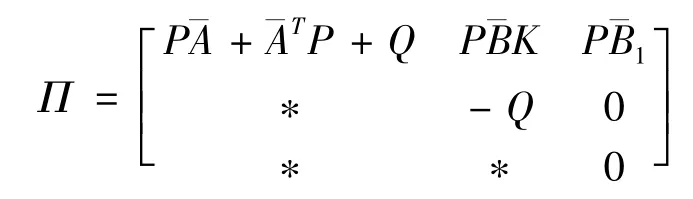
with the condition（7a），we have

Multiplied the upper formula（9）with e-αt，we obtain

Furthermore

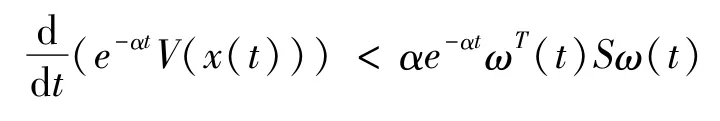
Integrating from 0 to t on both sides of the upper side，it follows that

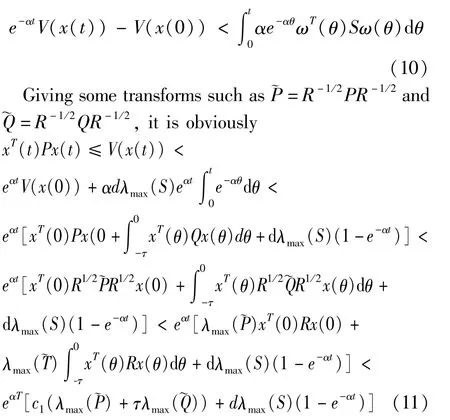
On the other hand，it yields

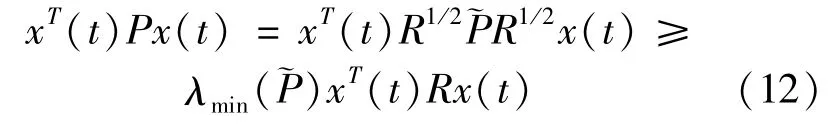
From（11）and（12），the following inequality can be obtained

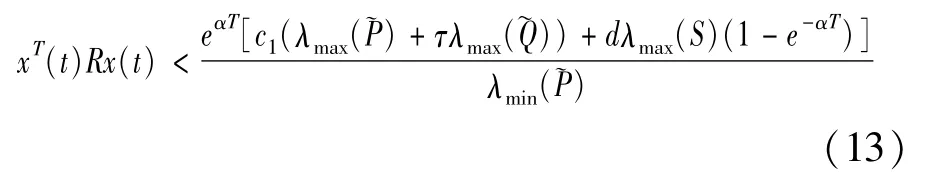
Combining（7b）and（13），it imply

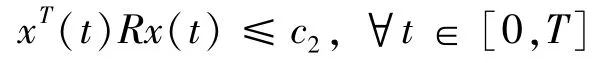
with the definition1，the system（5）is finite-time stabile.

2.2 The linearization of the finite-time stability condition

Theorem 2.For the given three positive scalars c1，c2，T，with c1＜c2，a positive definite matrix R，thesystem（5）is finite-time stabile via state feedback u（t）＝¯KX-1x（t）with respect to（c1，c2，T，R，d）if，there exist scalarsα≥0，λi＞0，i＝1，2，3，εj＞0，j＝1，2，positive definite matrices X∈Rn×n，¯Q∈Rn×n，S∈Rl×l，and matrix¯K∈Rm×nsuch that the following linear matrix inequalities hold

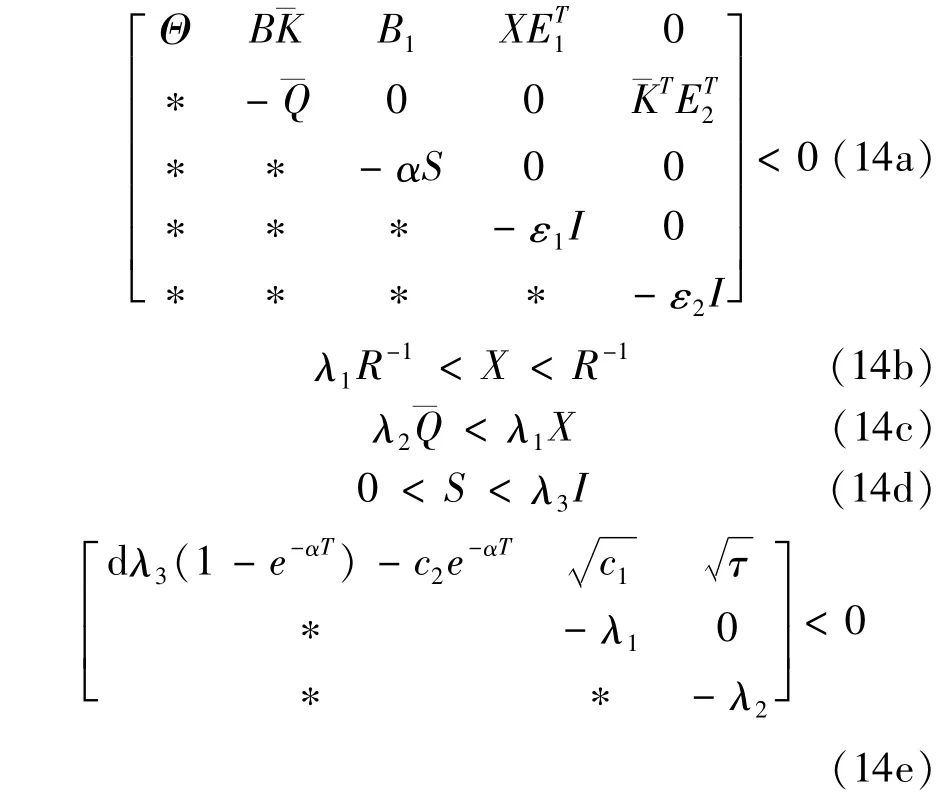
where

Proof.The condition（7a）can be rewritten as

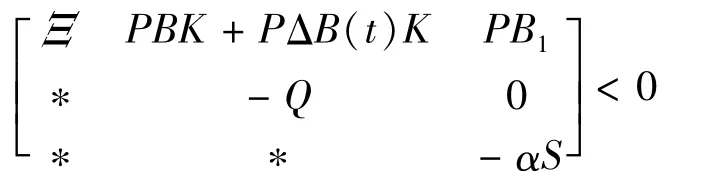
where

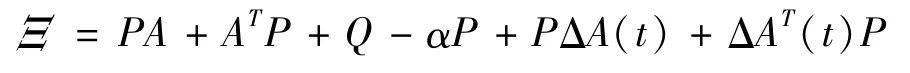
Therefore

With Lemma1，we obtain that the above inequality is equivalent to

where

With lemma 2，we know that the above inequality is equivalent to

where

Pre-and post-multiplying the above inequality by block-diagonal matrix diag｛P-1，P-1，I，I，I｝，we know the inequality（7a）is equivalent to

where

On the other hand，we denote

Consider that R is the positive-definite matrix and

Now the inequalities（14b-14d）imply that

With Lemma 2，we know the inequality（14e）is equivalent to

With（16），the condition（7b）follows that

Inserting the inequality（17）into（18），the inequality（7b）is satisfied.This completes the proof.

Remark.The conditions in Theorem1 and Theorem 2 are not linear matrix inequalities with respective to α，c2，sinceα，c2appear in a nonlinear fashion.However，once we fixα，they can be turned into linear matrix inequalities based feasibility problems which can be solved via the linear matrix inequalities Toolbox of MATLAB.

3 Numerical Example

In this section，we compare the results of this paper with those of reference［12］through a specific example.For simplicity，we consider the networked control system（3）with structural uncertainty and jamming attack，where0.1，ω（t）＝0.6cos t.

Using the design method in reference［12］，the controller is obtained as follows

On the other，the state feedback controller of the system is obtained by solving linear matrix inequalities（14）in this paper

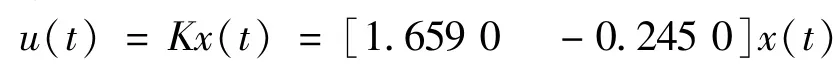
3.1 Comparison of simulation results of the system states

In order to compare the simulation results of system states under different algorithms，the initial condition is selected as

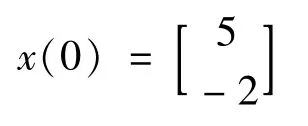
the response curves system states x1（t），x2（t）are Fig.2 and Fig.3.

Fig.2 The response curves of the system state x 1（t）

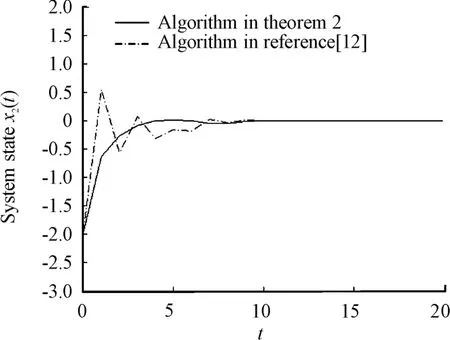
Fig.3 The response curves of the system state x 2（t）

In Fig.2 and Fig.3，the solid line is the simulation curve of the system state by using the algorithm in theorem 2 in this paper，and the dot-dashed line is the simulation curve of the system state by using the algorithm in reference［12］.In Fig.1，the convergence speed of the solid line is faster than that of the dotdashed line.The solid line converges to the origin in 10 seconds，while the Dot-dashed line converges to the origin after 10.Moreover，the smoothness of the solid line is obviously better than that of the dotdashed line.In Fig.2，although the convergence time of the solid line and the dot-dashed line are within 10 seconds，the effect of the solid line is better from the perspective of smoothness，and there is no significant oscillation phenomenon，while the dot-dashed line has not only a large oscillation，but also a large overshoot.In a word，the design method proposed in this paper is better than that in reference［12］.

3.2 System performance comparison

Next，we use the decentralized IAE function as the performance index to evaluate the system performance，and compare the system performance under the two control strategies

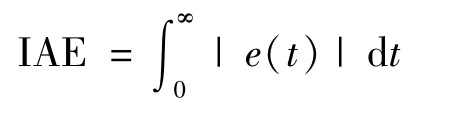
The curves of IAE function that use algorithm in theorem2 in this paper and the algorithm in reference［12］are shown in the Fig.4.

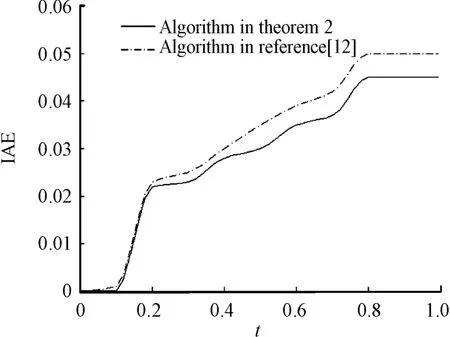
Fig.4 The curves of lAE of the two algorithms

The solid line is the IAE function curve obtained by the algorithm in theorem 2 in this paper，and the dotted line is the IAE function curve obtained by using the algorithm in reference［12］.As can be seen from Fig.4，the performance changes caused by the algorithm in this paper are significantly smaller than those in reference［12］over time.Therefore，the algorithm in this paper can improve the system performance more effectively than the algorithm in reference［12］.

4 Conclusion

This paper provides a sufficient condition for the finite-time stability of the networked system，which can be solved by LMI toolbox in MATLAB.When the LMI is feasible，the explicit expression of the desired finitetime control is also given.The purpose of this paper is to provide an effective way to reduce the influence of network induced delay on the network system，improve the finite-time transient performance of the system，and solve practical problems in network engineering.In addition，it is worth mentioning that our results can be extended to other types of networked system，such as distributed delay，fast varying delay，random delay，etc.，which will be our next research work.