Determination method of the autocorrelation coefficient of the fault factors in the house of availability of complex products

Shu-guang SUN，Xue-hua LIANG，Meng ZHANG，Gui-xiang SHEN，Xin GUAN

（1Business School，Shandong Normal University，Jinan 250358，China）

（2 School of mechanical and aerospace engineering，Jilin University，Changchun 130022，China）

（3School of business and Economics，Shandong University of Finance and Economics，Jinan 250200，China）

Abstract：In the house of availability（HOA）of complex products，the accurate calculation of the autocorrelation coefficient of fault factors is conducive to obtain the accurate weight of the fault factors，which is targeted at establishing the availability guarantee mechanism.Therefore，this study presents a method，which considers a number of expert opinions and influencing factors，to figure out the autocorrelation coefficient of fault factors.The fuzzy causal relationship between the fault factors are expressed as an extension interval number，which is converted into the determined value using the extensible analytic hierarchy process（EAHP）.Then，the autocorrelation coefficients between the fault factors are obtained.The method considers all of the various influence factors of the fault factors and their fuzziness，which ensures that the accuracy of the calculated autocorrelation coefficients is high.Finally，the method is validated by using a series of machining centers as an example.

Key words：House of availability，Fault factors，Autocorrelation，Extensible analytic hierarchy process

1 Introduction

The house of availability（HOA）of complex products is proposed based on the existing CNC machine tools HOA［1-3］and is the expansion of the existing HOA of CNC machine tools in application.The HOA model of complex products defines“what to do”and“how to do”using the quality function deployment（QFD）method and achieves the transformation of the user’s needs by building a series of houses of quality.Specifically，the functions of complex products and the characteristics of failure factors are combined，and the coupling relationship between reliability，maintainability，and availability is considered.The present work aims to start from the users’needs in the market for product availability；adopt the fault mode，effects，and criticality analysis method to ensure that the user’s demand for the availability of complex products is gradually decomposed into the product chain of product design，manufacturing，assembly，outsourcing，installation，operation，and maintenance；and construct the theoretical system of the availability guarantee mechanism for complex prod-ucts.

The key inputs in the HOA model of complex products include the user availability requirements and failure factors，the correlation matrix between user availability requirements and failure factors，and the autocorrelation matrix of failure factors.The establishment of the autocorrelation matrix of the fault factors is the key content of building the HOA model.The correctness of the autocorrelation matrix has a significant influence on the accuracy of the output information of the HOA model.Of the domestic and international studies conducted，only few consider the method of determining the autocorrelation coefficient of fault factors for complex products.However，in the research on the autocorrelation coefficient of the engineering properties of QFD，many exploratory studies are available for reference.The expert scoring method is used in analyzing the production process or market competition information to clarify the autocorrelation of all engineering characteristics［4］.The analytic hierarchy process（AHP）method is used to determine the autocorrelation of engineering characteristics to avoid the poor consistency of the conclusions obtained by the scoring method［5］.The analytic network process（ANP）is used to establish the theoretical model of the relationship between customer demand and engineering characteristics［6-7］.However，when the ANPmethod is adopted，with the increase in the correlation between the elements，the pairwise comparison matrix of the required evaluation and the comparison problem increase geometrically，which in turn increases the complexity of the calculation.Moreover，the analysis of autocorrelation involves considerable fuzzy information.When handling a large amount of information，the method is prone to many problems.Therefore，several studies have used fuzzy theory to analyze the autocorrelation of engineering characteristics［8-10］.However，the membership degrees or membership functions，which are difficult to determine，usually need to be determined in advance.Rough set theory is used to determine autocorrelation in a previous study［11］.However，many problems with regard to accuracy are still encountered.

Therefore，in view of the scarcity of research on this topic，an HOA model of complex products is constructed in the present work.The extenics method is also adopted to determine the autocorrelation coefficient of the fault factors，which guarantee the subsequent establishment of complex products HOA.

2 Construction of the HOA model of complex products and analysis of the Extensible Analytic Hierarchy Process（EAHP）principle

2.1 Construction of the HOAmodel of complex products

A HOA model of complex products is constructed based on the QFD method and the HOA model of CNC machine tools（Fig.1）.

Fig.1 HOA model of complex products

To meet the goal of obtaining the ultimate satisfaction degree of user requirements with minimal input for availability improvement.The relationship between user requirements and the failure factors of complex products is established and the key failure factors that have a significant effect on the availability demand are explored using the HOA model of complex products.The output items of the floor are obtained based on the input item information in the model and with the aid of the calculation of the model.Then，the failure factors of complex products that play a key role in satisfying the users’overall needs are identified.This study focuses on the analysis of“roof”in the model and lays the foundation for obtaining the accurate importance of the failure factors of complex products.

2.2 Analysis of the EAHP principle

The matter of ascertaining the correlation coefficient between fault factors is essentially an index-weighting problem.Therefore，the EAHP is adopted to ascertain the correlation coefficient between failure factors in this study.The judgment matrix constructed using this method is an extension interval number，which can express the fuzziness of human judgment.The process of determining the autocorrelation coefficient using theEAHP is as follows：

2.2.1 Establishment of the extension judgment matrix

Definition 1［12］：Set E（U）as an whole extension set on domain U.Set a＝a-，a＋∈E（U）.The simple correlation function Ka（u）can be represented as follows：

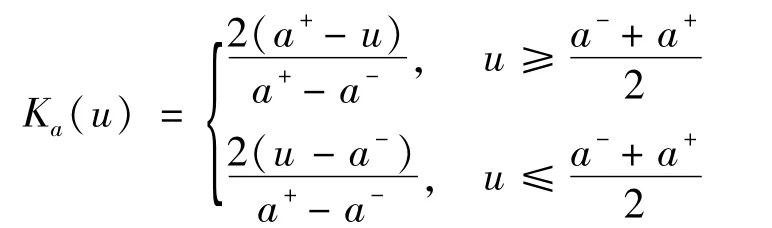
For a certain failure factor，one or several fault factors associated with it can be identified through analysis.N fault factors related to a fault factor are regarded as indicators.The correlation between these indicators and the fault factors is compared in pairs.Then，the extension judgment matrix A is obtained.

Table 1 1-9 scale method

2.2.2 Aggregation of the extension judgment matrix

The members of the HOA group of complex products are the experts in this field.Given the different knowledge and experience of experts，the degrees of reliability and influence on the conclusions of the same problem vary，such that the relative weight of each expert is also different.In this study，different weights are given to each group of experts.E sets of experts are employed to determine the correlation coefficient.Their weights are p1，p2，…，pE，pr∈［0，1］andrepresents the extension judgment matrix that is obtained from the evaluation of E group of experts of the same problem.is set as the extension interval number determined by the r group of experts.The matrix is aggregated by the common addition aggregation method［13］and expressed as follows：

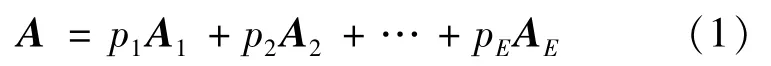
Where A is the addition convex combination of A1，A2，…，AE.The comprehensive interval number of an index in A can be expressed as

2.2.3 Consistency test of the extension judgment matrix

The comprehensive extension judgment matrix A can be obtained using Formula（1）.The aggregated judgment matrix not only can eliminate the influence of subjective factors but maintain and advance the consistency of the judgment matrix.However，the number of fault factors corresponding to each failure factor in the method is different，which is likely to cause the inconsistency of the relationship between the failure factors and a certain fault factor.

Theorem 1［12］：Set A＝（aij）N×Nas an extension interval number judgment matrix.Ifaiecan be derived for any i，j，e＝1，2，…，N，then A can be considered an extension interval number consistency matrix.

If the comprehensive judgment matrix A obtained using Formula（1）is inconsistent，then it needs to be checked for consistency.It is necessary to convert the extension interval number judgment matrix into a general judgment matrix to make the extension interval number judgment matrix conform to the consistency ratio method in the AHP method.The steps of consistency check are as follows：

Step 1.The extension judgment matrix is generalized.A＝（aij）N×Nis set as an extension interval number judgment matrix.According to the symmetry of the number of extension intervals，the middle value ofis calculated as follows：

The term of the generalized extension judgment matrix A′is recorded as A′＝（a′ij）N×N.

Step 2.The eigenvector of A′is calculated.Given that A′is a general extension judgment matrix，the eigenvector method can be used to compute its eigenvectorsω＝（ω1，ω2，…，ωN）T，as shown as follows：

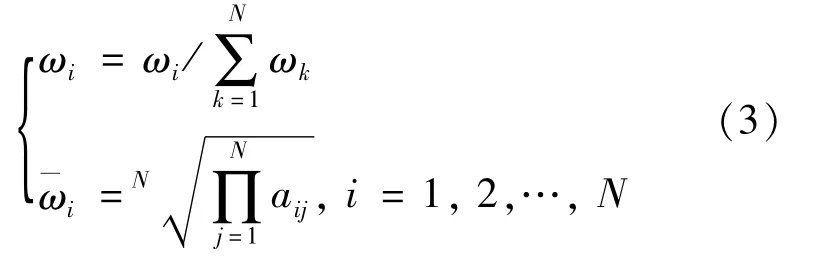
Step 3.The maximum characteristic root of A′is calculated as follows：

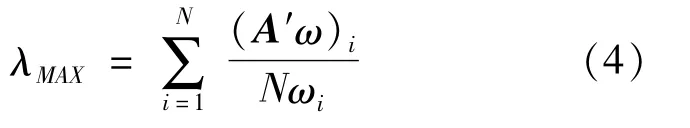
Where（A′ω）irepresents component i of vector A′ω.

Step 4.The consistency index is calculated as follows：

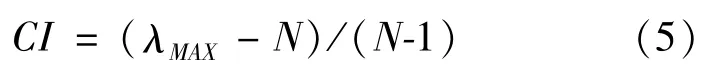
Whereλmaxis the largest characteristic root of A′，and N is the number of failure factors related to the fault factors.

Step 5.The consistency ratio is calculated as follows：

Where RI is the average random consistency index，which can be determined using the values listed in Table 2.When CR＜0，the consistency of the judgment matrix is satisfactory.

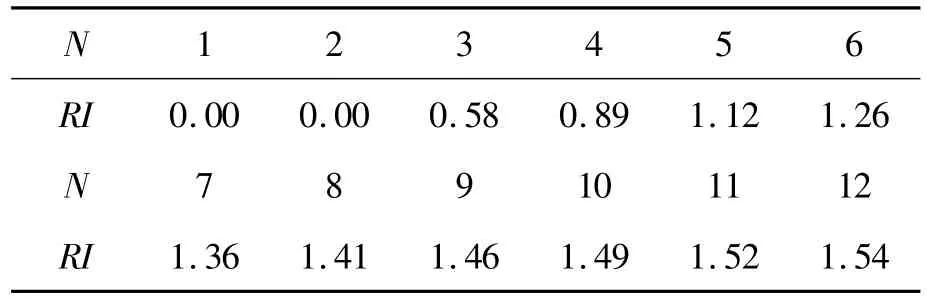
Table 2 Numeric table of RI

2.2.4 Calculation of the autocorrelation coefficient of the fault factors

The following theorems are introduced to calculate the autocorrelation coefficient of the fault factors more accurately：

Theorem 2［12］：Let A＝（aij）N×Nbe an extension judgment matrix that has met the consistency test.xand x＋are normalized eigenvectors with the positive components of A-and A＋under the maximum eigenvalue，respectively.A sufficient and necessary condition for the entire eigenvectorω＝kx-，mx＋＝（ω1，ω2，…，ωN）Tof A under the maximum eigenvalue to satisfyis expressed as follows：

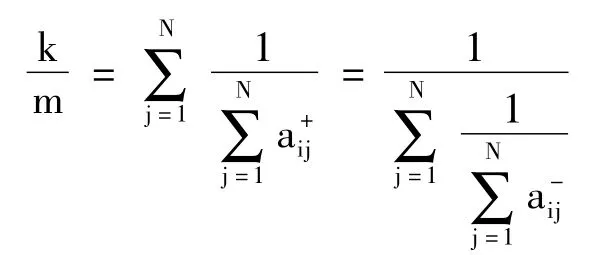
Given the concrete expression ofand the symmetry of the left and right endpoints of the weight vector，the following equation can be derived：

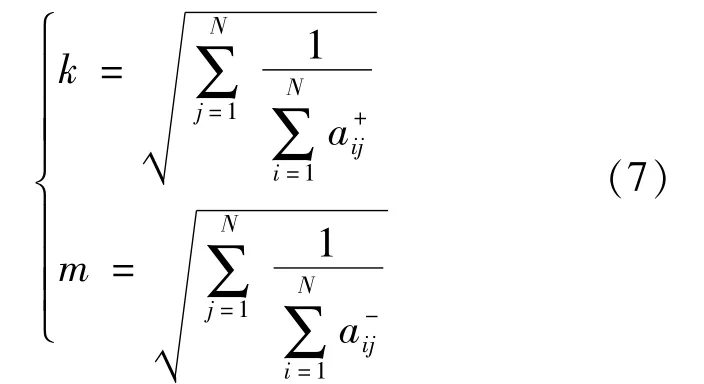
Theorem 3［14-15］：Set a＝a-，a＋，b＝b-，b＋as two extension interval numbers，and the possibility V（a≥b）of a≥b can be obtained using the formula VLet A＝A-，A＋be the extension judgment matrix of the correlation coefficient between a fault factor and the related failure factors and suppose that it has passed the consistency test.In ascertaining the correlation coefficient between the fault factors and the various failure factors，follow these steps：

Step 1.Calculate the normalized eigenvectors x-，x＋with positive components corresponding to the maximum eigenvalues of A-，A＋.

Step 2.Calculate the values of k，m according to Theorem 2.

Step 3.Calculate the correlation coefficient vector according to S＝（S1，…，S2，…，SN）T＝kx-，mx＋，where S1，…，S2，…，SNare the interval numbers.

Step 4.Calculate the correlation coefficient between a fault factor and all of the related failure factors.Let Pidenote the correlation coefficient between a fault factor and item i-related failure factors.The interval numbers in the correlation coefficient vector can be figured out by Theorem 3.The possibility of Si≥Sj（i，j＝1，2，…，N）is V（Si≥Sj）.If V（Si≥Sj）≥0，then D1＝0，Di＝V（Si≥Sj），where D＝（D1，D2，…，DN）Trepresents a correlation coefficient vectorbetween a fault factor and all of the related failure factors.The maximum value max（D1，D2，…，DN）Tin D＝（D1，D2，…，DN）Tis set as 9.Then，the ratio of each correlation coefficient to the maximum is calculated one by one and is multiplied by 9.The specific integer value is obtained by the rounding method.

3 Example

A case study of a series of machining centers HOA is conducted to verify the model and algorithm of autocorrelation determination based on the EAHP.In this study，the failure factor refers to the subsystem of the machining center.From the combination of the fault data and the experience of experts，the extension judgment matrix is obtained by the 1-9 scale method shown in Table 1.Each table has two groups of different matrices，which are provided by two groups of different experts（see the examples in Table 3）.For the tool magazine，the tool magazine is compared with the pneumatic system.The first group of experts think that the tool magazine has a greater influence on itself than on the pneumatic system.The number of extension intervals is between 4.7 and 5.3，that is，the extension of interval is［4.70，5.30］，which is equivalent to“5”in the 1-9 scale method but is not the number 5.Conversely，the extension interval between pneumatic system and tool magazine is［1／4.70，1／5.30］compared with the influence on the tool magazine，which is equivalent to 1／5 but is not 1／5.The second group of experts believe that the influence of the tool magazine on itself is greater than that of the pneumatic system.The extension interval is［4.6，5.4］.The extension interval of the pneumatic system to the tool magazine is［1／4.6，1／5.4］，compared with the influence on the tool magazine.The two extension interval number judgment matrices obtained are elastic and reasonable.The two groups are assigned the weights of 0.6 and 0.4.Table 3 presents the results of the aggregation and consistency tests of the extension judgment matrix.

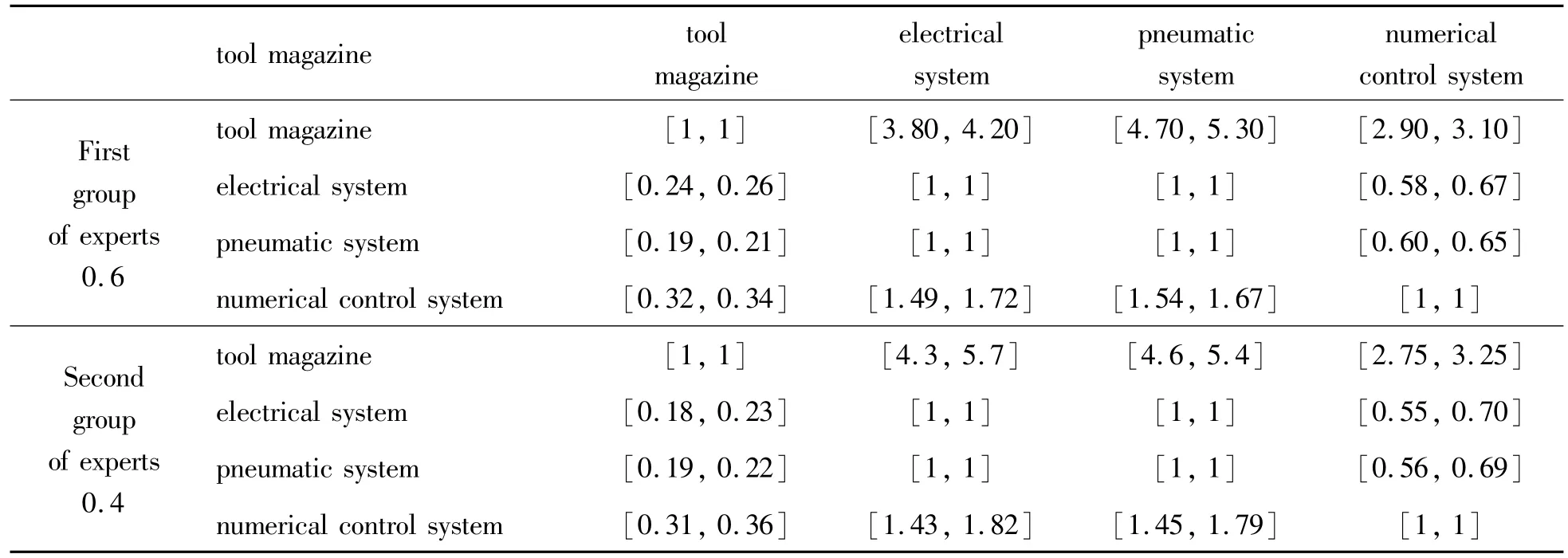
Table 3 Extension interval number judgment matrix of subsystems that have an influence on the tool magazine

According to the data shown in Table 2，the following judgment matrix after the assembly of complex products is obtained using Formula（1）：

The following generalized matrix A′Mis obtained using Formula（2）：

The following feature vector of matrix A′Mis obtained using Formula（3）：

The following maximum eigenvalue of matrix A′Mis obtained using Formula（4）：

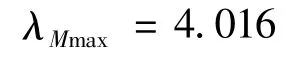
According to Formulas（5）and（6），CRM＝5.99×10-3＜0.1.Therefore，the generalized matrix A′Mhas passed the consistency test，that is，the extension judgment matrix after passing is checked by the consistency test.

The aggregated extension matrix AMis decomposed into the following expression：

The characteristic vectors are counted as follows：

kM＝0.980，mM＝1.017 are obtained using Formula（7）.Accordingly，

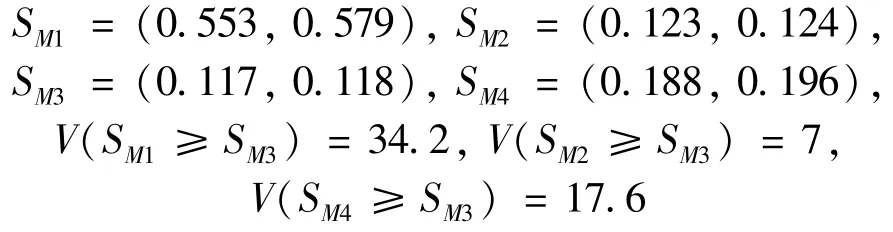
The maximum value of 34.2 is set as equivalent to 9.Thus，the correlation coefficients among the tool magazine，electrical system，pneumatic system，CNC system and the tool magazine are obtained as 9，2，1，and 5，respectively.

In the same manner，the autocorrelation coefficient of each fault factor can be obtained.The correlation coefficient of the roof of the machining center HOA and the autocorrelation matrix of the fault subsystem of the machining center are obtained（Fig.2）.

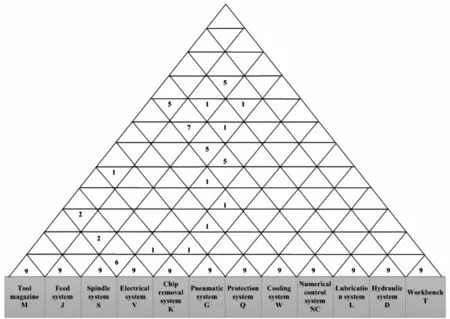
Fig.2 Roof of the machining center HOA

Note：The number in the upper triangle shows the influence of the front subsystem on the rear subsystem，and the number in the lower triangle indicates the influence of the rear subsystem on the front subsystem.A greater numeric value indicates a more serious influence.

4 Conclusion

（1）This research extends the application scope of the theory of a specific product—CNC machine tools HOA.It makes the theory universal.

（2）Through the combination of the analysis and refinement of fault data and expert judgment，the fuzziness judgment of fault subsystem correlation is expressed as an extension interval number.Then，the extension interval number is converted to a definite value by the EAHP method.Finally，the autocorrelation matrix between fault subsystems（factors）is obtained.The autocorrelation matrix is used to solve the problem of fuzzy assignment between fault factors caused by experts’cognitive differences.Meanwhile，the HOA output item—the importance of the fault factor—is more accurate.Accordingly，the designed availability guarantee mechanism can meet the usability technology requirements and satisfy the users’needs.