基于Winkler模型的沿空留巷底板变形力学分析*
刘高林 阮永芬 魏德永 王雨洁 刘克文
(1.昆明理工大学建筑工程学院 昆明 650500; 2.云南建投第一勘察设计有限公司 昆明 650031)
0 引言
在煤炭开采过程中,通常采取先挖巷道再逐步开采巷道左右两侧煤炭的方法,为保证开采巷道的安全,对采煤巷道底板受力变形的研究尤为重要。龙驭球[1]采用半无限弹性体理论,即假设地基为均质、连续、弹性的半无限体,将地基的计算分为平面问题和空间问题进行求解。丁敏等[2]假设弹性地基梁两端自由,求解出了弹性地基梁在任意荷载作用下的挠度方程。李顺群等[3]结合Winkler弹性地基梁经典公式p=kω,将地基梁转化为无限长梁,求得其转角θ、弯矩M和剪力Q。华心祝等[4]认为上部岩层掉落出现集中应力,并传递到巷道底板导致底板受力变化,这是产生底臌的主要原因。上述研究并未对巷道底板的内力变化给出确切的计算公式或计算公式较为复杂,本文利用Winkler弹性地基梁理论,建立巷道底板在顶板岩层垮落荷载作用下的受力模型,用解析解推导出巷道底板的内力、转角、位移及挠度公式,分析出沿空留巷底板破坏机理,为相应防控措施的提出提供理论依据,为巷道设计及工程施工提供分析计算公式,确保采煤巷道底板的变形及受力在允许范围内,保证其安全运行。
1 沿空留巷受力力学模型的建立及分析
结合巷道实际情况建立力学模型进行分析,为简化计算将底板当作弹性体,减去上覆原岩应力γh,煤矿边界处看作固定支座,取单位长度进行分析。按弹性地基梁原理建立力学模型进行分析。图1为巷道左侧开挖后采空区顶板岩块A、岩块B在重力影响下发生垮落,若不做防护措施,垮落岩层将堵塞巷道,影响采煤工作开展。为保证巷道正常工作,可在巷道内架设混凝土支护,巷道右侧为煤帮,即右侧均布荷载q,顶板将在支护外侧发生断裂,断裂后垮落在底板上产生的荷载分布如图2所示,荷载最大值为hq0,其中h为应力集中系数,巷道左侧荷载为q1,左侧边界处荷载为q0,底板反力为kω,其中k为地基系数,巷道底板力学分析模型如图2所示。在侧墙极限平衡区取dx段岩体进行研究,建立其弹性地基梁力学分析模型如图3所示。

图1 煤矿开采示意

图2 巷道底板力学模型

图3 微元体力学分析
Winkler对地基模型提出以下假设:地基表面任一点的沉降ω与该点所受的压力p成正比[5],即
(1)
侧墙微单元体的静力平衡条件为
V+bpx-V+dV-qxdx=0
(2)
式中,b为侧墙沿隧道纵向的长度。进而可得
(3)
材料在一定荷载作用下,转角与挠度、弯矩、剪力、荷载呈导数关系[6],即
(4)
(5)
(6)
可简化为
ω'=θ
(7)
EIω''=M
(8)
EIω'''=F
(9)
EIω(4)=Q
(10)
式中,ω为挠度;ω、ω、ω、ω(4)为挠度的导数;θ、M、F、Q分别为底板转角、弯矩、剪力、荷载;E为弹性模量;I为惯性矩。
根据巷道底板力学模型,可得底板各段所受荷载为
(11)
高阶线性微分方程的解为通解+特解,即
(12)
ω11x=eαx(A1cosαx+A2sinαx)+e-αx(A3cosα+A4sinαx)
(13)
(14)
式中,g为式(11)中不含ω项;A1~A4、B1~B4、C1~C4、D1~D4为各段中的积分常数。以0 (15) 由式(2)~(4)可知,分别对ωx求一、二、三阶导数,可求出巷道底板转角θ、弯矩M及剪力F。 (16) (17) (18) 根据连续条件和支撑条件确定各段中的积分常数[7]。根据巷道底板力学模型可得 (19) (20) (21) (22) (23) 利用MATLAB可计算出积分常数如下:A1=0.003 04,A2=-0.000 263,A3=-0.046 2,A4=-0.057 1,B1=0.000 035 8,B1=-0.000 446,B3=-0.023 2,B4=-0.435,C1=0.000 007 99,C2=-0.000 006 59,C3=-1.34,C4=-0.488,D1=-0.000 023 8,D2=0.000 897,D3=-1.92,D4=1.66。 将积分常数代入式(15)~(18),可求得巷道底板挠度、转角、弯矩、剪力,如图4~图7所示。 结合图4~图7与工程经验可知,巷道底板的破坏主要由两方面原因造成:一方面,随着采空区不断增大,上覆岩块会慢慢垮落,从而导致底板所受应力增加,造成底板剪切破坏,如图7所示,巷道底板剪力最大约为7 kN;另一方面,巷道开挖与采空区增大的过程相当于卸载过程,从而引起巷道底板产生负弯矩,发生弯曲破坏,如图6所示,巷道底板弯矩最大约为16 kN·m。根据两种破坏形式可采取以下防护措施:①排出地下水,设置竖向排水井,以加快土体固结的速度;②夯实或更换表层土体中抗剪强度较小的土层,增加底板承载力;③锚注加固底板,根据底板不同硬度采取相应的加固措施,对于硬度为中硬及以上的底板可通过打底板锚杆进行防治,对于松软底板可进行灌浆加固;④综合考虑整个结构,尽量使巷旁支护宽度、刚度与底板的强度相匹配[9]。 图4 巷道底板挠度曲线 图5 巷道底板转角曲线 图6 巷道底板弯矩曲线 图7 巷道底板剪力曲线 (1)利用Winkler弹性地基梁理论,计算推导了任意荷载下巷道底板的挠度、弯矩、剪力、转角公式。 (2)结合大量工程实例得出,巷道底板破坏形式大多为剪切破坏,主要原因是随着煤矿的不断开采,上覆岩层因垮落传递给巷道底板的力就会增加,这时底板所受剪力也会增加。为防止巷道底板发生剪切破坏,可通过对底板进行灌浆、更换抗剪强度较小的土层等方法,提高巷道底板抗剪强度,预防因底部剪力过大而发生剪切破坏。 (3)此方法计算结果与实际情况大致相符,且计算简单,可为此类工程的设计施工提供经验。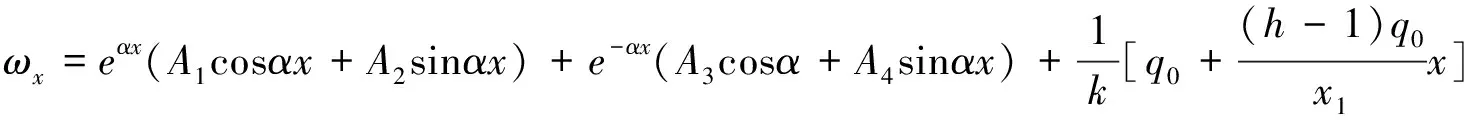

2 算例应用
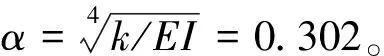




3 结语

