水泥环性质对套管破坏的影响分析*

朱庆杰 李莉 陈艳华 李雪 智睿

(1.常州大学石油工程学院 江苏常州 213164； 2.华北理工大学地震工程研究中心 河北唐山 063210)

0 引言

在油田中，套管因失去水泥环保护，从而造成裂缝、错断变形的现象时有发生[1]。失去水泥环保护的套管不仅影响着井筒的完整性，而且在油田生产作业中存在极大的安全隐患。由于井筒所处的地下环境复杂，作业时储层中的流体与固体相互耦合，因此有必要针对性地研究在多孔介质流固耦合作用下，套管破坏受水泥环材料性质的影响。

自20世纪90年代以来，众多学者在水泥环性能方面进行了深入的研究。李早元等[2]、GUO B Y等[3]、ZHANG H 等[4]从水泥材料方面分析了水泥的受力性能；李军等[5]、张景富等[6]、郭雪利等[7]从水泥环形状、尺寸等物性方面分析了其对套管的应力影响；LIU K等[8]、李娟等[9]、郭辛阳等[10]研究了水泥的膨胀性能对井筒的破坏影响。同时，还有部分学者侧重研究水泥环受不同荷载条件的破坏影响，如：党旭光[11]分析了地层蠕动对井筒的影响；ELAHEH A 等[12]、WANG W 等[13]等分析了不同外界环境压力荷载下的水泥环完整性。然而，目前的研究通常忽略了套管受地层中流体与水泥环两者耦合作用产生的影响，较少考虑流体与固体的耦合作用于水泥环-套管结构，从而影响研究结果的准确性和可靠性。

本文研究了多孔介质流固耦合作用下，水泥环对套管的保护作用。应用地层流固耦合理论和有限元数值分析，建立套管-水泥环-地层的三维有限元数值模型，研究套管的应力受水泥环的参数性质和不同水泥材料的影响。为减少实际工程中的套管破坏、延长套管使用寿命提供了参考。

1 计算方法

在有限元建模中，使用Parasolid建模方法，建立地层-水泥环-套管的固体模型；在流体分析模块中建立流体模型。通过流固耦合计算，将固体模型和流体模型进行有限元模型的流固耦合求解。

1.1 多孔介质流固耦合的有限元计算

流固耦合界面的求解,其位移协调条件为

(1)

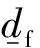
(2)

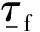
依据运动学条件，在流固耦合界面，流体在固体节点产生的流体力可表示为

(3)

式中，hd为固体位移的虚拟量。

由以上公式可知，固体和流体模型在耦合区域包含相同的位移、速度和加速度。而在耦合区域中，设定流体应力作为附加内力加在固体模型上，此时固体模型的柯西应力表示为

(4)

式中，pl为张量表示的流体应力，MPa；τs为固体节点到流体边界的应力，MPa。

在多孔介质域中，可以通过插值得到流体压力和节点位移。其孔隙度表达式为

(5)

式中，φ为岩石孔隙度；J为几何单元雅克比；J0为初始雅克比；φ0为初始孔隙度。

渗透率表达式为

(6)

式中，k为当时的岩石渗透率；k0为初始渗透率。

在多孔介质流固耦合分析中，通常是流体应力影响着多孔介质变形，固体位移影响着流体流动，这被称为双向耦合。双向耦合的求解方法分为直接计算法和迭代计算法，通常采用迭代计算法。这是因为迭代计算法不仅适用于瞬态分析，具有节省内存和使用条件广泛的优势；而且此方法也适用于稳态分析。

耦合系统的求解矢量可表示为

X=(Xf，Xs)

(7)

式中，Xf为流体节点求解矢量；Xs为固体节点求解矢量。

用固体位移和流体应力表示的流固耦合系统有限元方程为

(8)

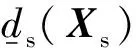
1.2 套管破坏准则

当外载荷对套管产生不均匀作用力时，套管可能发生塑性变形；当套管材料的抗载强度不及外载荷时，可能会造成材料的破坏。本构体使用API套管，其厚度与外径之比>0.04，不会发生失稳破坏现象，故只需要考虑套管的塑性屈服破坏。

在外载荷条件下，一般金属变形的应力应变曲线如图1所示。

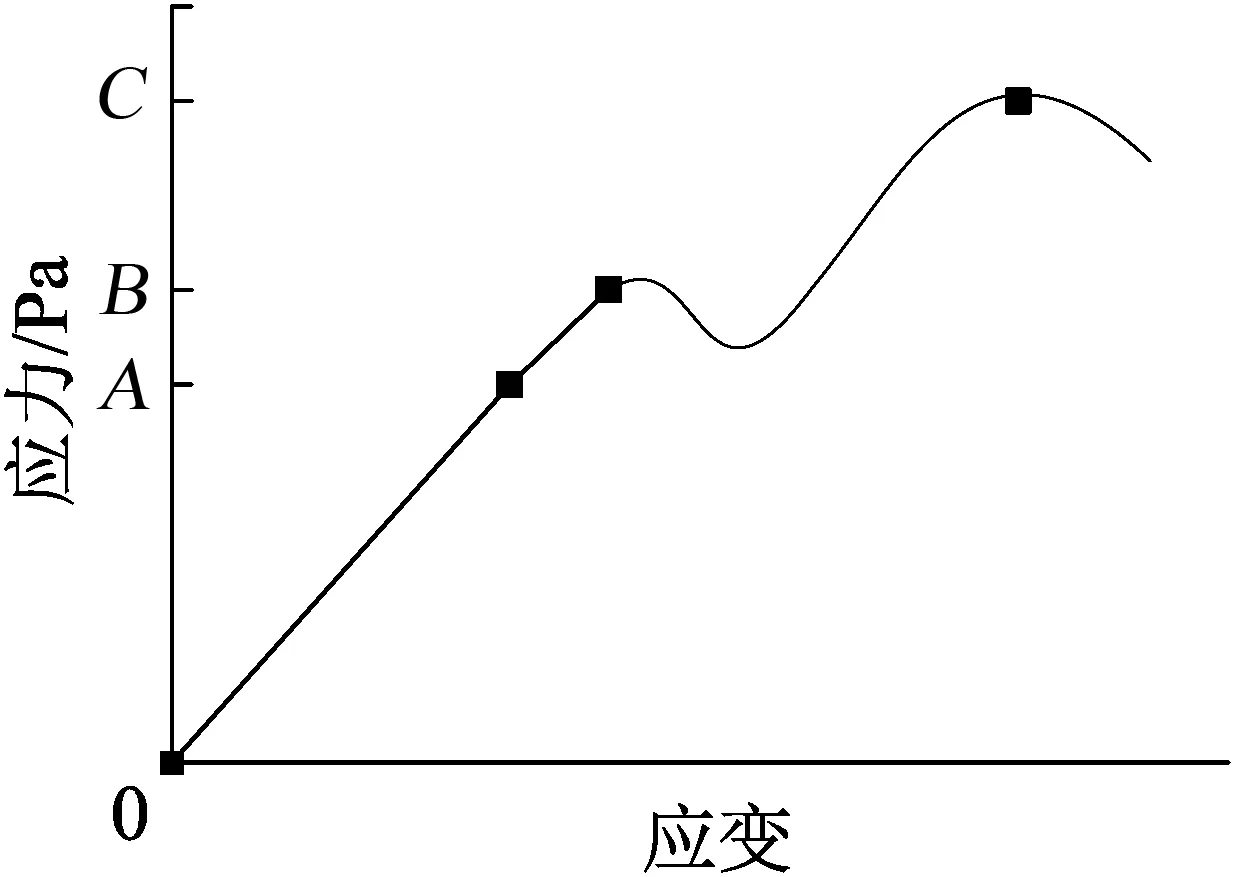
图1 金属材料的屈服曲线

图中，A代表材料的弹性极限，B代表材料的屈服强度，C为材料的抗拉强度极限。当材料应力超过A时，应变关系偏离胡可定律；当所受应力超过B进入屈服阶段，即超过弹性极限后，材料的塑性应变骤然增加，材料产生变形；当材料受到的应力值持续增加并进入强化阶段，此时即C为材料抵抗破坏的最大能力。

在判断套管的屈服变形状态时选择Mises屈服准则。该准则常在金属材料屈服中被使用，认为材料的屈服状态是由外载荷决定，物体的形变到达某一程度，只要承受的等效应力满足要求，则该处就开始进入塑性状态。

(9)

式中，σs为材料的屈服点；σx为x轴主应力；σy为y轴主应力；σz为z轴主应力；τxy为xy方向切应力；τyz为yz方向切应力；τxz为xz方向切应力。材料发生屈服的条件为f≥0。

2 有限元建模

2.1 固体几何建模

依据辽河油田锦州采油厂某区块地质数据，建立地层-水泥环-套管基本模型。用Parasolid建模方法建立地层，并将地层划分为上部盖层、中间储层和下部地层，然后定义中间储层为多孔介质材料，最后将水泥环和套管加入到地层中，建立好的固体几何模型如图2所示，二维的井筒平面模型如图3所示。

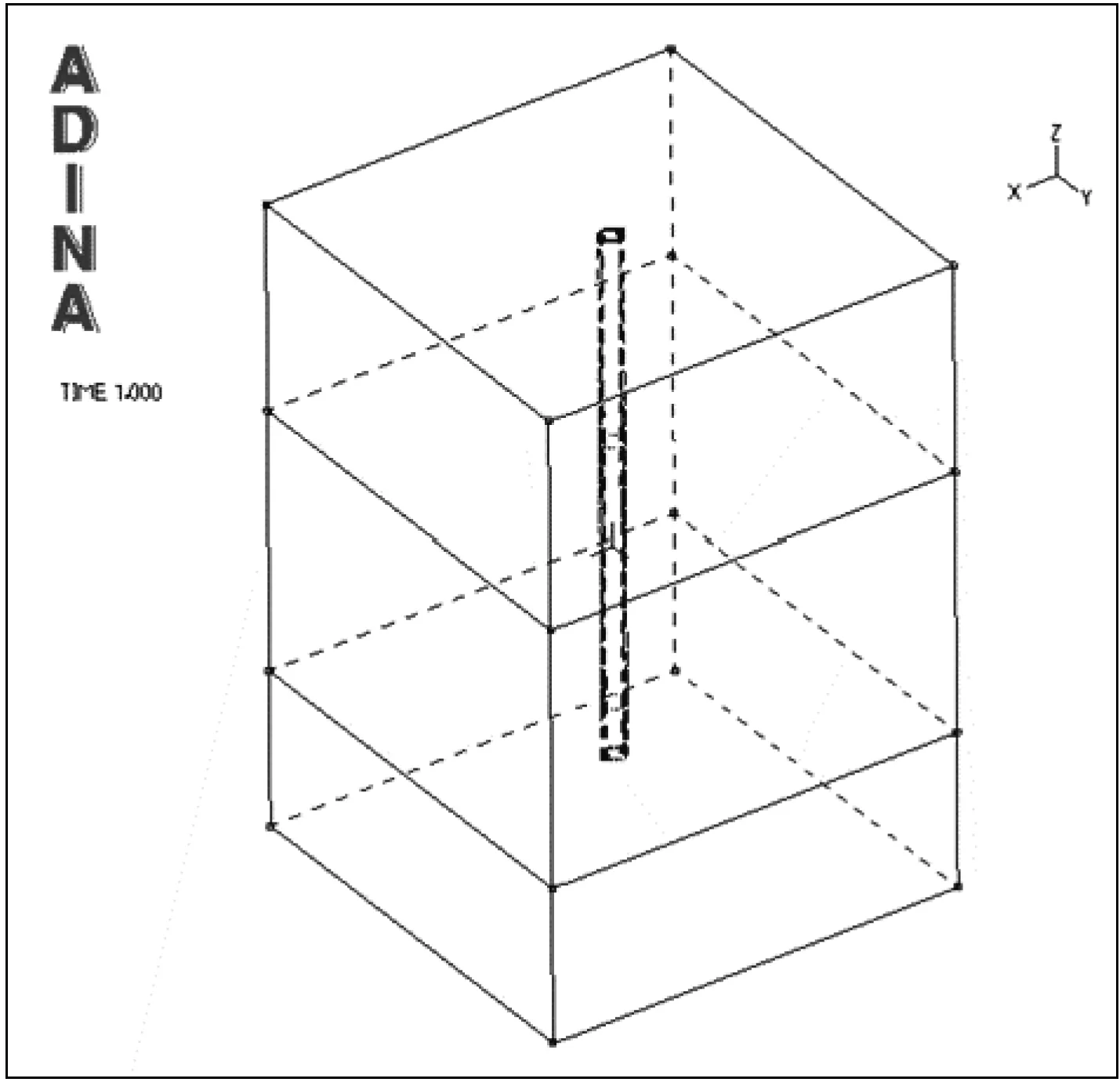
图2 地层-水泥环-套管的几何模型

图3 井筒二维模型

2.2 流体几何建模

流体模型部分与固体建模方法类似，但它是在CFD模块中瞬态分析模式下进行建模。因此，可在流体分析类型模块中采用“Copy F.E.Model…”命令，将固体几何模型复制到流体分析模块的建模界面。此外，还需要在模型侧面的流固耦合界面构造流入边界的流体。然后使用Parasolid建模方法，在井内建立圆柱体，视为井筒中的热流体，建立完成的流体模型及标注如图4所示。

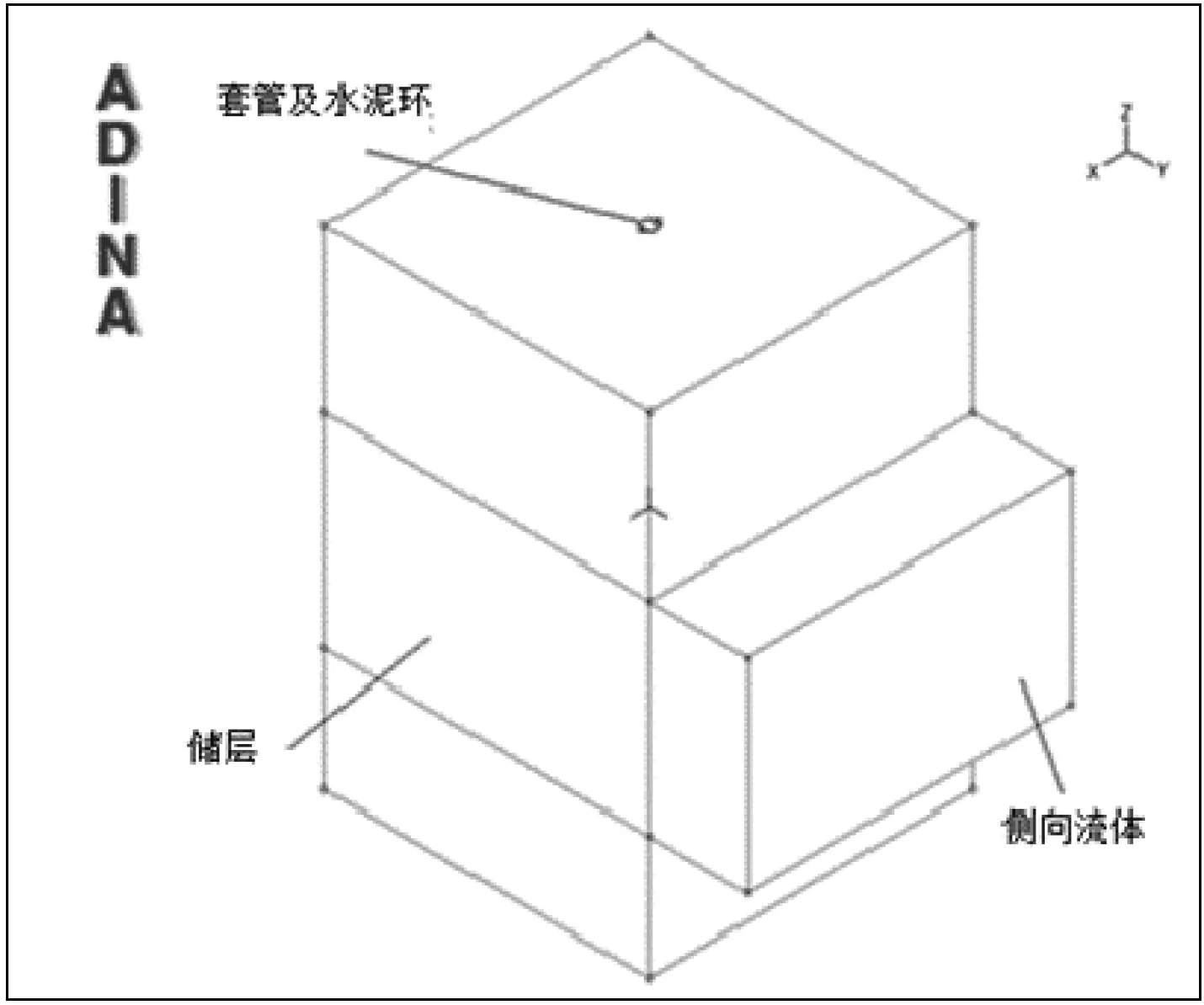
图4 流体的几何模型

2.3 材料参数

对照实际情况建立的地层-水泥环-套管有限元模型，其材料模型、岩土模型均采用理想的莫尔-库伦材料。套管采用多线性塑性材料，水泥环采用双线性塑性材料。生产套管的规格选用N80Φ177.8 mm×8.05 mm，热膨胀系数为2×10-5。水泥环厚度设定为21 mm。套管材料的应力应变关系曲线如图5所示。各类材料的参数性质见表1，模型中流体的材料参数见表2。

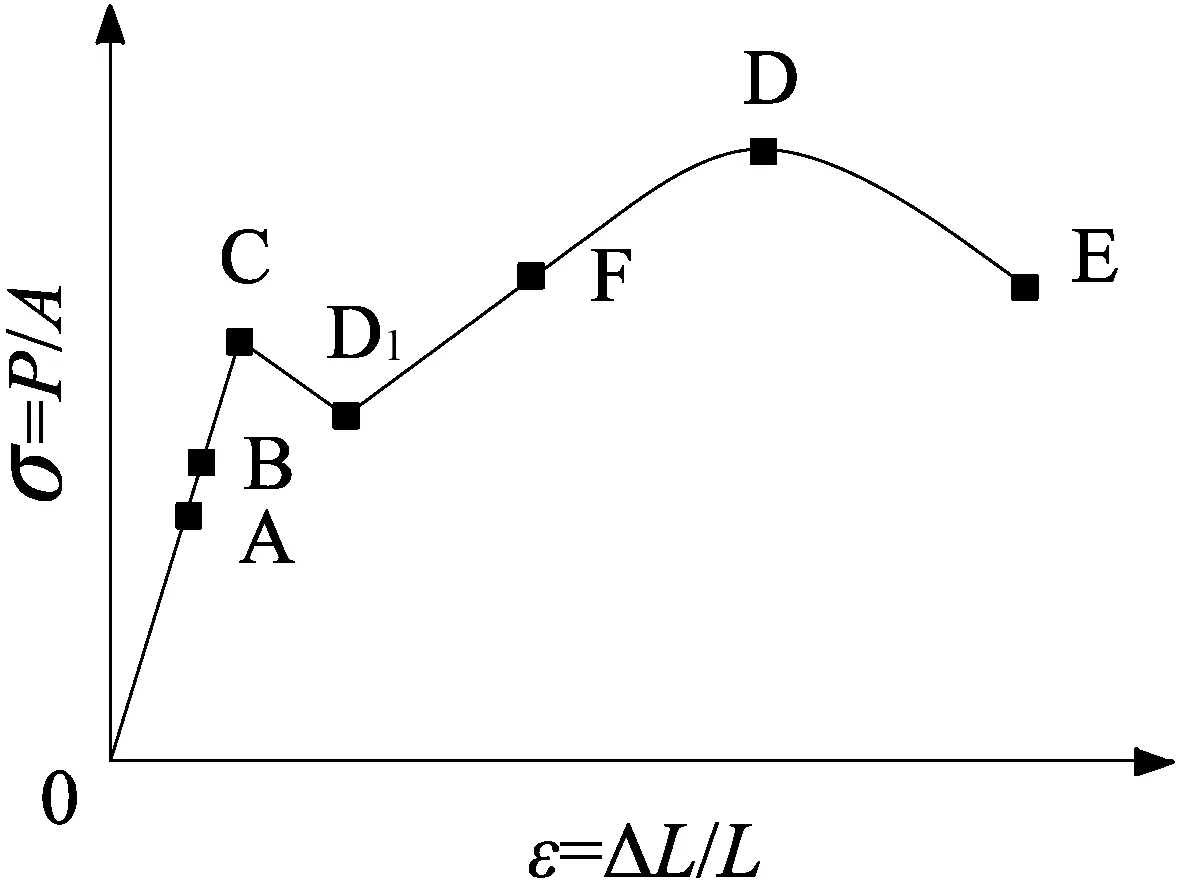
图5 塑性材料的应力应变关系曲线

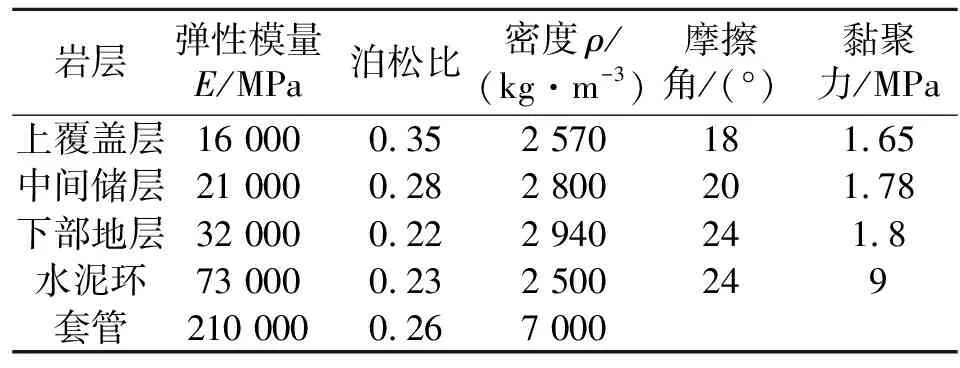
表1 各材料的参数定义

表2 模型中流体的材料属性

2.4 模型边界条件

在模型上施加荷载时，通过设定时间步长和时间函数来实现加载，时间函数为线性增长的函数。在结构模型上覆盖层的上表面施加岩层压力20 MPa，在分析套管受破坏时，采用拟动态分析的方法，即在模型中设定Low Speed Dynamics。由于模型中上覆岩层压力一直存在，因此其时间函数为某一常数。在流体模型中进行载荷设置，选取20 MPa的侧向流体压力模拟储层地层压力，侧向流体压力的时程如图6所示。

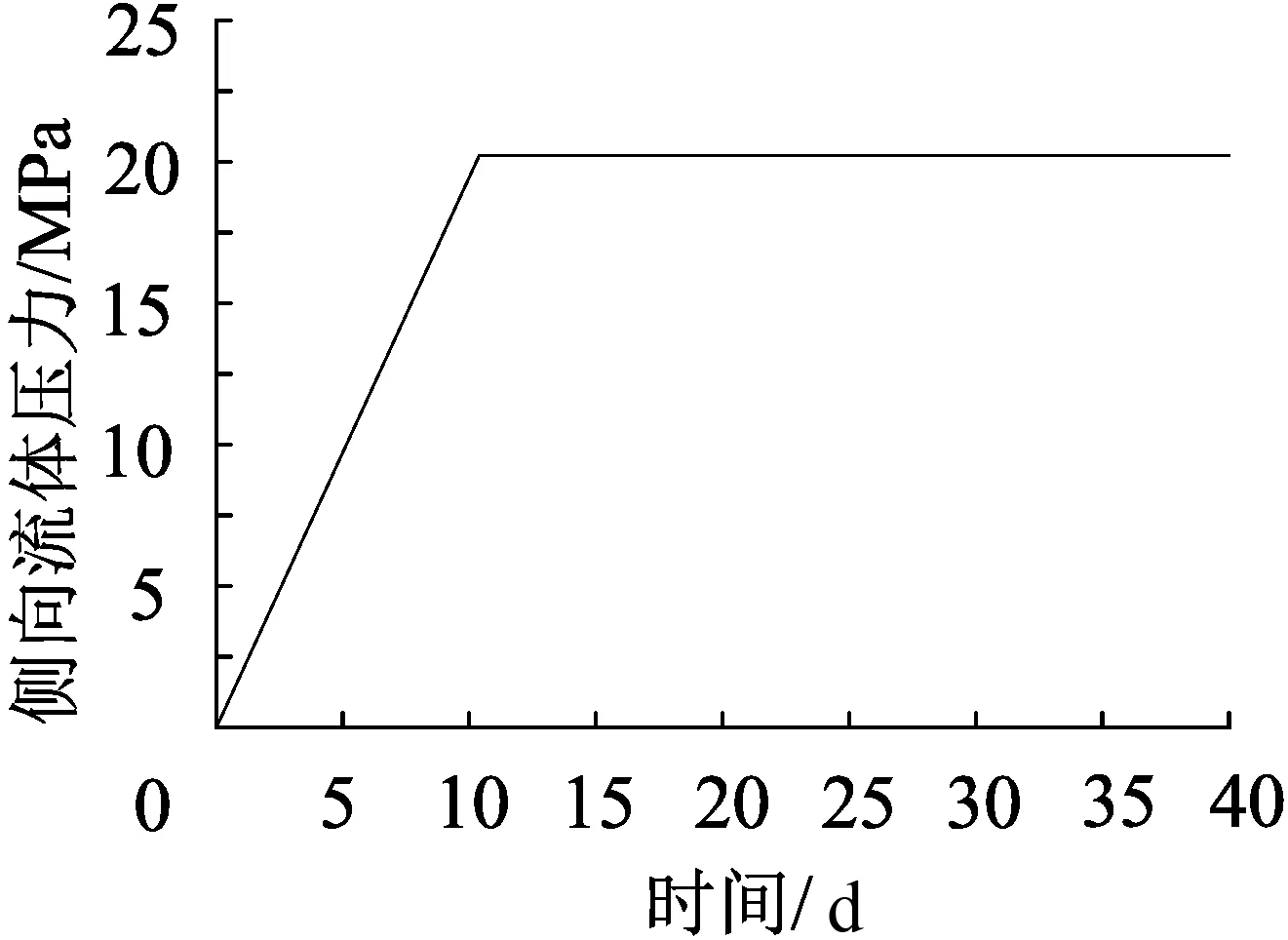
图6 荷载时间函数关系

由于本模型的有限元计算和观测重点是套管和水泥环部分，因此对套管和水泥环的网格划分采用外疏内密的形式，按照0.1倍的指定单元长度进行网格密度划分；岩体模块的网格密度采用0.5倍的指定单元长度划分；储层以0.3倍的指定单元长度划分；井口外边线为圆形，划分方法选细分份数为4。选择三维四节点的自由网格对土体部位剖分，选用八节点的高阶3D实体单元对水泥环和套管部分进行剖分。

根据实际油井开采的接触情况设定模型的接触方式。在模型中，井壁与油藏储层接触处、储层地层与其侧向流体接触处以及多孔介质储层内均发生流固耦合作用，因此设定流固耦合边界。第一类流固耦合边界为井筒的井壁处地层；第二类流固耦合边界为流体流入的边界面，即储层外表面。

3 计算结果分析

常规采油井通常需要用水泥进行固井，将套管与周围地层胶结封固，是固井过程中重要的一环。然而从现场实际情况来看，水泥环通常易受高压等条件限制，从而产生裂纹甚至断裂，导致套管受到内外压等因素影响造成变形扭曲，如图7所示。

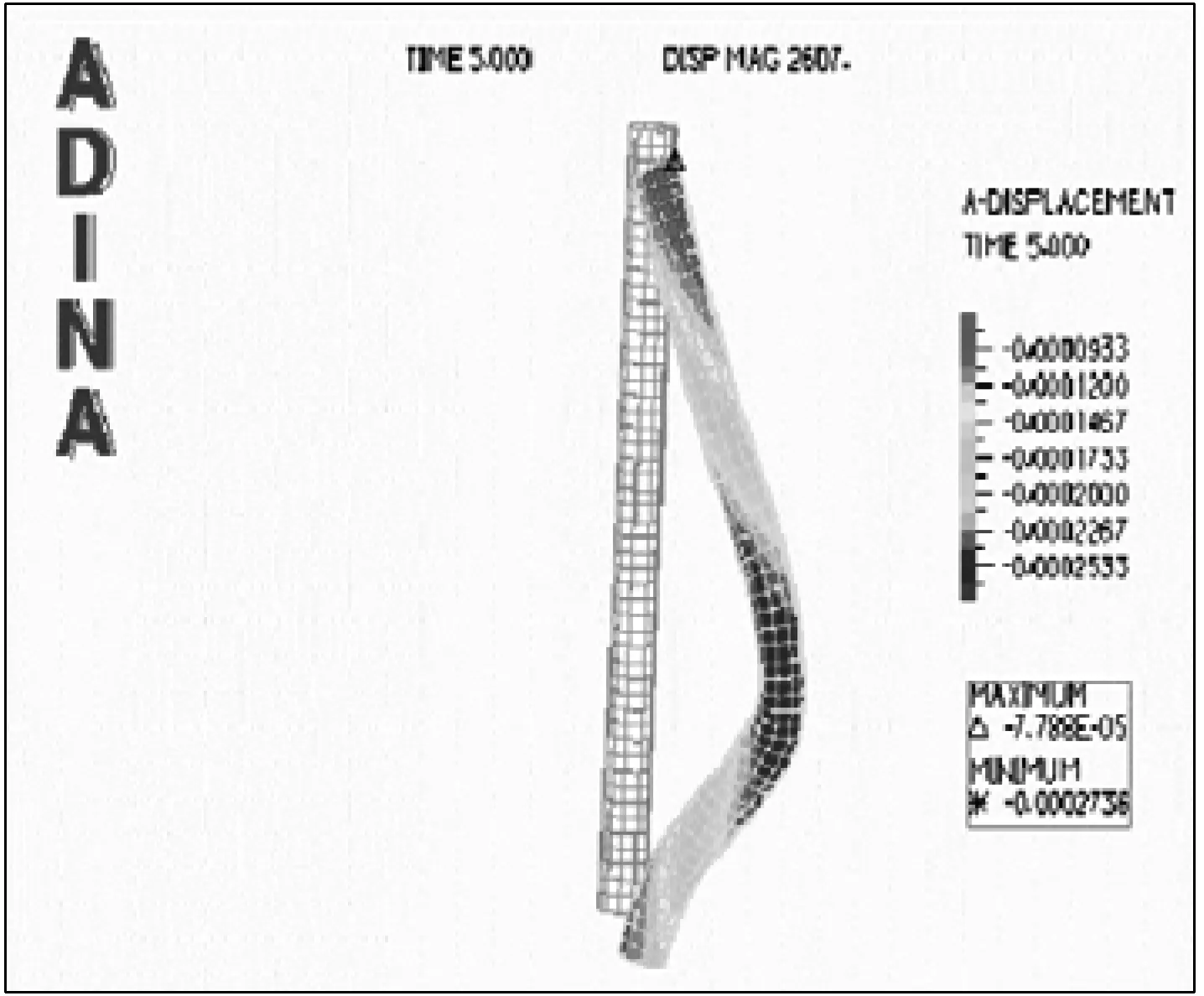
图7 套管受力变形

3.1 水泥环的影响

采用上述模型，选取Φ177.8 mm×8.05 mm的生产套管为研究对象，井眼尺寸为Φ222.2 mm，选取未固井套管与合格固井套管为研究对象，模拟多孔介质流固耦合作用对套管有效应力的影响，如图8所示。

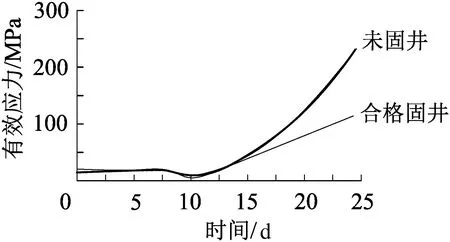
图8 井筒有效应力时程

由图可得，随着采井时间的增加，未固井中的套管比合格固井中的套管所承受的有效应力大，并呈逐渐增大的趋势。因此，未固井的套管更易受到剪切变形，完整水泥环的存在对套管有明显的卸载作用，对套管破坏起到保护作用。

3.2 水泥材料的性质

3.2.1 水泥环泊松比的影响

一般水泥泊松比约为0.18，高性能水泥的泊松比范围为0.18～0.28。不论其他条件如何改变，水泥环弹性模量均保持为20 GPa，其泊松比分别取0.18、0.23、0.28，其他设定条件与前文一致，得到套管受水泥环的不同泊松比的有效应力时程，如图9所示。

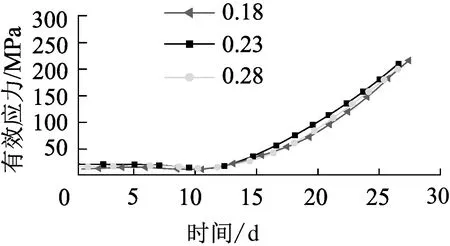
图9 水泥环泊松比变化的影响

由图可看出，3条曲线基本重合，即水泥环泊松比分别为0.18、0.23、0.28时，套管的应力变化趋势基本一致，说明了套管的有效应力受水泥环不同泊松比的影响较小。在前11 d左右的时间里，套管受到水泥环泊松比的影响较小；但在12 d之后，泊松比对套管有效应力的影响随时间的增加而逐渐增大。

3.2.2 水泥环类型的影响

在油井下，受温度和压力因素的影响，对水泥性质的要求各不相同，因此本文选用普通水泥、高强水泥和膨胀水泥为研究对象，研究这3类水泥环所受环向应变的影响，如图10所示。可以看出，随着时间的增加，普通水泥环的环向应变逐渐增大；高强水泥环的环向应力约从第14 d开始骤然增大，可能是因为高强水泥环虽然强度高，但其刚度也高所致，若适当降低刚度，高强水泥环应力的承载能力将相应增加。与其他两类水泥材料相比，膨胀水泥环的环向应变较小，原因在于膨胀水泥环在作业过程中产生的膨胀应力与外载荷可以部分抵消，进而减小了水泥环的应力应变，使得水泥环起到了良好的保护套管的作用。

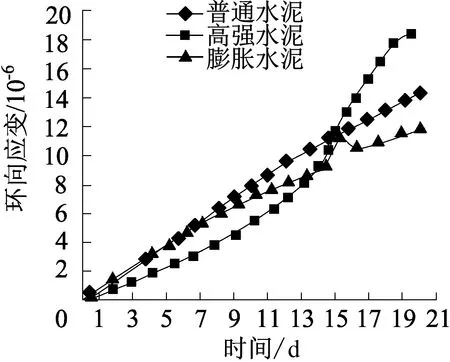
图10 不同类型水泥环的环向应变时程曲线

4 结论

(1)在多孔介质流固耦合作用下，水泥环对套管起到一定的保护作用。水泥环可以减小套管受到的有效应力，并对套管破坏具有明显的卸载和保护作用。

(2)通过对套管所受有效应力的分析可知，在不同泊松比的水泥环影响下，水泥环的泊松比对套管应力影响较小，在选择水泥浆时，可着重考虑其他因素影响。

(3)通过对普通水泥环、高强水泥环和膨胀水泥环所受的环向应变分析可知，膨胀水泥产生的膨胀应力在较大程度上减少了水泥环中的切向拉应力，有效地预防了水泥环的破坏，从而保护了套管。

(4)建立地层-水泥环-套管有限元模型，采用流固耦合计算方法研究套管破坏问题，更加贴合实际地下工程状况，为今后研究套管破坏问题提供了理论依据。