基于子图演化与改进蚁群优化算法的社交网络链路预测方法

顾秋阳，琚春华，吴功兴

（1.浙江工业大学管理学院，浙江 杭州 310023；2.浙江工业大学中国中小企业研究院，浙江 杭州 310023；3.宁波诺丁汉大学商学院，浙江 宁波 315175；4.浙江工商大学管理工程与电子商务学院，浙江 杭州 310018）

1 引言

近年来在线社交网络规模和用户数量日益增加，链路预测作为社交网络分析中的一个新兴课题，现有研究往往根据社交网络图中现有节点及链接属性来预测2 个节点之间的新链接[1]。链路预测的目标为通过考虑社交网络图在时刻t的快照，预测出该网络图在时刻t+1 可能产生新链接，而时刻t+1 可能是拍下快照后的一周、一个月、一年，甚至几年[2]。Liben-Nowell 等[3]将社交网络中的链路预测视为挖掘链接的子集。链路预测可用于许多不同的应用中。王智强等[4]等认为在许多网络中，由于信息或数据带有噪声，会产生一些不必要的链接，可以借助于链路预测方法来检测这些不必要的链接，可用于通信侦察领域。其通过对社交网络进行链路预测得到了网络的演化模型，使研究者能更好地了解网络。Huang 等[5]提出了基于链路预测算法的新型似然方法，使用社交网络图对传染病的患病率进行建模，每个预测链接均显示了社会中潜在的感染区域。Yin 等[6]在社交网络环境中，通过预测用户中的共同兴趣来发掘新好友（即新链接），此类推荐也会增加用户对社交网络的忠诚度。Pech 等[7]通过分析客户购物情况进行链路预测，形成客户商品推荐，优化推荐系统，提升了预测成功率。

如今常用的链路预测方法可分为两大类，即有监督式方法和无监督式方法。在预测链接时不需要任何先验知识或培训的为无监督式方法，而使用该网络训练所得的模型及先验知识来预测链接的为有监督式方法。无监督式方法大多使用网络相似度度量及结构属性来实现链路预测，且不需要进行任何训练。Wang 等[2]认为两节点之间最短路径的长度和公共邻节点的数量都可视为结构属性，这些属性均可以用于链路预测。Jaccard 等[8]提出的Jaccard系数等方法类似于公共邻点，而不同之处在于，在这种相似度度量方法中，如果两节点所拥有的公共邻点较多、非公共邻点较少，则两节点越靠近彼此。节点度数也是社交网络环境中预测新链接的关键结构属性之一，即节点度数较高的2 个节点以后彼此交互的可能性更大，这种方法又被称为优先链接[9-11]。而近年来，某些链路预测算法所用的方法是基于特殊子图的演化，此部分将在第2 节进行详细介绍。最大似然方法为典型的有监督链路预测算法。Wu等[12]介绍了一种由网络数据推导的层次结构似然估计方法（系统树图），而概率模型也可视为有监督式链路预测算法。王凯等[13]利用二元分类器进行链路预测。虽然有监督式方法考虑了每种网络的特殊性，但可能会耗费大量时间，且不适用于大型网络[14]。

蚁群优化（ACO,ant colony optimization）算法最早由Dorigo 等[15]提出，旨在解决困难的组合问题。蚁群优化算法以蚂蚁的觅食行为为基础，认为蚂蚁在觅食时会随机搜寻周围环境；在发现食物后，蚂蚁会检查食物的数量和质量并取走一块食物；在回家的路上，蚂蚁会沿途释放一种叫作信息素的化学物质，信息素的数量与食物源的数量和质量成正比。信息素即为蚁群间的协同机制，可让它们找出食物源到家的最短路径[15]。本文拟使用蚁群优化算法对所研究的问题进行建模，主要包括以下3 个步骤。

步骤1设蚂蚁k由社交网络图中节点i遍历至节点j的概率为，如式(1)所示。

其中，τij为边信息素数量，ηij为由节点i移动至节点j的成本，Ni为节点i的邻节点集，系数α和β分别为蚁群优化算法的基本参数。本文假设所有边都具有初始数量的信息素。

步骤2无论何时使蚂蚁都能找到食物为该问题的理想解，且每只蚂蚁在从食物源到家的沿途上都会释放信息素，如式(2)和式(3)所示。

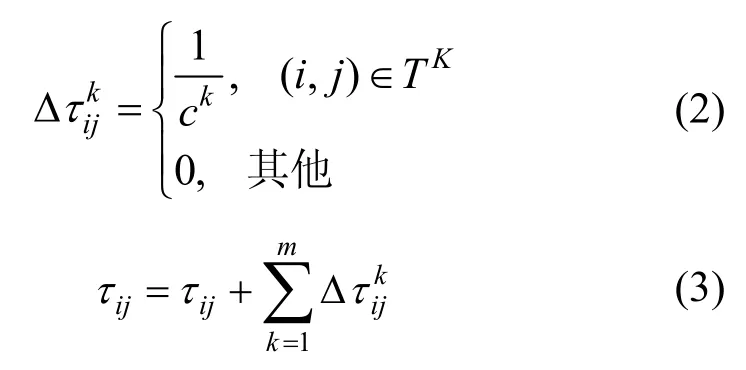
其中，TK为蚂蚁k所遍历的由家至食物源的路径，其长度为ck；m为现有蚁群的总数，表示找出由食物源至家的最短路径。本文假设每条边上的信息素都会逐渐消退；路径越拥挤，其上保留的信息素就越多。

步骤3分析信息素的消退机理，如式(4)所示。

其中，ρ为基本参数。

本文首先以子图演化的链路预测为基础，在社交网络图中确定特殊子图。然后，研究子图演化以预测图中的新链接，并用蚁群优化算法来定位特殊子图。最后，本文针对所提方法使用不同的网络拓扑环境与数据集进行实验，以期为社交网络环境的优化、链路的预测、监控与追责提供实验依据；同时也为大众更好地使用社交网络提供指导意见。

本文的主要贡献包括：1) 提出了一种基于子图演化与蚁群优化算法融合的社交网络链路预测方法，提升了预测精度；2) 证明了图形结构在链路预测算法中起到重要作用；3) 相对于图神经网络及图深度学习等热门链路预测方法，SE-ACO 算法能够有效地缩短运算时间。

2 文献回顾

2.1 文献综述

由于本文所提方法运用蚁群优化算法找出了特殊子图，因此本文将介绍基于子图查找和演化的链路预测方法。本文所提方法与其他方法的最大区别在于将蚁群优化算法首次用于链路预测过程中。Fadaee 等[16]认为通过找出一定时间间隔内的三元组演化模型，可预测出2 个连续社交网络快照间的新链接，其所述方法为有监督式结构链路预测算法。如果该图为有向图，则会有64 个三元组，在每个三元组中的每2 个节点之间有4 种不同的关系：一个双向链接，2 个单向链接，一个无链接。计算2个连续社交网络快照上的64 个三元组可得到三元组转换矩阵（TTM,triad transition matrix），基于此可找出 2 个非连接节点之间的链接概率。Lichtenwalter 等[17]提出了一种新型有监督式社交网络链路预测及分析算法，旨在找出社交网络图的子结构，也称为顶点配置结构（VCP,vertex collocation profile）。张子柯等[18]将聚类系数的定义进行扩展，提出了一种新型概率链路预测算法。聚类系数是社交网络图中的三元组变为三角关系的趋势，式(5)展示了如何计算社交网络图中的聚类系数。

Zhang 等[19]研究了有向网络中的特殊子图，认为这些子图代表有向网络中的微观组织原理，并表明，这些子图中在社交网络中较普遍。最优的有向网络局部结构是包括4 个节点与4 个有向链接的Bi-Fan 结构，胡文斌等[20]基于聚类机制（CM,clustering mechanism）和潜在理论（PT,potential theory）证实了上述观点，即如果子图是仅比Bi-Fan结构少一个链接的子图，则创建该链接的概率将是最高的。郭丽媛等[21]采用谱聚类（SC,spectral clustering）的方法对社交网络的链路预测进行研究，通过降维方法获得简易矩阵,采用该矩阵能够提高预测效果；其不仅计算了类内节点之间的相似度，还计算了不同类之间的节点相似度。Gong 等[22]首先提出了一个特征转化方法，该方法能够把原有特征进行简化，提高了链路预测精度；其次构建基于受限玻尔兹曼机的深度学习算法进行链路预测。这种无监督算法仅使用小样本训练即可取得良好效果。

目前在社区发现和预测这一领域，图神经网络（GNN,graph neural network）和图搜索聚类算法也表现出了较优能力。Gori 等[23]借鉴神经网络的研究成果，设计了一种用于处理图结构数据的模型。Bronstein 等[24]对图结构数据和流形数据领域的深度学习方法进行了综述，侧重于将所述各种方法置于一个称为几何深度学习的统一框架内。白铂等[25]提出了一种新的图神经网络分类方法，重点介绍了图卷积网络，并总结了图神经网络方法在不同学习任务中的开源代码和基准。Fan 等[26]将图神经网络提取的物品特征和节点特征，通过多层感知机进行评分预测推荐。郭嘉琰等[27]指出了在不同GNN 变体中出现的相关聚集过程，但也发现了以图神经网络为代表的方法通常时间成本较高。

2.2 文献评述

通过对现有研究成果的梳理发现，社交网络中的链路预测方法已经受到了国内外学者的重视并得到丰富的成果。上述研究成果对本文具有一定的借鉴意义，但也存在一些不足：1)已有很多学者对基于社交网络图的链路预测开展了一系列卓有成效的研究，但是多数将其定义为静态图（如李冬等[28]），鲜有基于子图演化进行动态社交网络链路预测的文献；2) 现有的社交网络链路预测方法大多基于数理推导（如Gao 等[11]），但很少有加入如蚁群优化算法等概率型路径寻优算法进行社交网络链路预测的文献；3) 几乎所有的相关文献都使用了例如BA 无标度网络（BA scale-free network）、WS 小世界网络（WS small world network）等人工网络进行实验（如方哲等[29]），很少有使用真实数据集对社交网络链路预测进行分析的文献记录；4) 几乎所有的相关文献都直接使用现有算法进行链路预测（如尚凤军等[30]），很少有使用改进算法对社交网络进行链路预测的文献。

基于以上综述，本文首先提出一种基于子图演化与蚁群优化算法融合的社交网络链路预测方法，以基于子图演化的链路预测为基础，在社交网络图中确定特殊子图；然后研究子图演化以预测图中的新链接，并用蚁群优化算法定位特殊子图；最后针对所提方法使用不同网络拓扑环境与数据集进行验证。

3 社交网络链路预测方法设计

3.1 方法设计总体思路

社交网络中的每个实体都可以用一个节点表示，2 个节点之间的关系可用链接表示。为预测2 个节点之间可能产生的新链接，那么这2 个节点之间至少应该有一个关联。另一方面，本文认为预测2个无任何关系的节点之间的链接为一项随机任务，特别是对于大型社交网络而言，该问题至关重要，这是由于人们可以从这些社交网络的预测列表中剔除许多候选链接。Lichtenwalter 等[17]认为这就是如果2 个节点之间最多相距2 个跳点，则大多数链路预测算法都认为这2 个节点之间有潜在链接的原因。故本文认为2 个节点链接的预测问题可以转化为预测社会群体中源节点和目标节点之间链接的问题。例如社会群体中的节点存在相似兴趣、利益或目标，则源节点与目标节点社会群体可能存在更多共同兴趣（即链接），则这2 个节点之间创建新链接的概率较高。社交网络中最简单的社会群体为单节点，在单个关系的无向网络中，单节点社群的源节点和目标节点之间至多存在一种关系。要对这2 个节点之间的链接进行预测，其之间就必须存在这种单一关系。为了对社交网络中的新链接进行预测，应考虑更复杂的社群，这些社群内部至少要存在2 个节点，且随着社群中节点数量的增多及源节点与该社群间关系的增多，源节点与社群中目标节点之间创建新链接的概率也会增大。

图1 单个关系无向网络中节点与社群间可能存在的交互关系

单个关系无向网络中某节点和某社群间可能的相关性如图1 所示。图1 中第一层显示了节点和社群的最简单关系，该层中单个关系无向网络中仅存在一个链接，如时刻t的快照所示。时刻t的快照表示一种网络结构，链路预测算法用该结构预测下个快照中的新链接。如前所述，每2 个实体间至少应有一个链接，这样才能预测下个快照中的链接。图1 中的2 个实体分别为左侧的源节点和右侧的目标社群。第一层中未保留链接来预测网络中的下一快照。第二层的目标社群由2 个节点组成，该层中时刻t的快照表示源节点与社群间的关联，时刻t+1 的快照表示可创建的可能链接（虚线）。由于所有链接和节点的权重相同，因此图1 中未描绘其他可能的同构交互。第二层中有4 种不同的关系，因此存在4 种不同的可能链接。第四层是本文关注点的重点，其群体结构为三角关系，左右两部分分别有2 个可能的链接。本文将讲述如何根据第四层的子图结构来预测链接。而第三层中为最常见的社交网络结构，在此不做赘述。图1 所示四大层次并不是如今算力所能解决的，还可以考虑更多节点、更复杂的群体结构，但由于找出这些的群体成本更高，因此本文未考虑更复杂的层次，仅示例社交网络中两实体间更复杂的交互层次交互关系，如图2所示。

图2 社交网络中两实体间更复杂的交互层次交互关系

图1 中的第四层定义了本文所述方法，具有一个节点和一个三角关系，且三角关系中至少存在一条公共边。第四层有2 个子图(a)和(b)。由于子图(b)的结构属性多于子图(a)，而结构属性越多，预测出正确链接的机会就越大，故子图(b)价值更大。为证明这一观点，本文对比了根据子图(a)与子图(b)所预测的链接的准确性。首先从社交网络样本中提取出子图(a)和子图(b)，然后考察了作为潜在链接的所有潜在链接（即图1 中的虚线），最后根据精度度量对比了这2 个子图所预测出的链接质量。对比结果显示本文观点是正确的，即如果使用更多的结构属性，可以更正确地预测链接。Huang[31]的实验也证实了该结论，具体遍历与循环数计算方式参考文献[31]。因此，根据黄璐等[32]提出的概率模型，子图(b)中仅有一条边不存在的概率要大于子图(a)中2 个链接都不存在的概率。本文对图1 的其他层也进行了同样的实验，并将其结果与第四层结果进行了对比，发现第四层中的子图结构更有利于社交网络情景中的链路预测，故本文用第四层的子图结构来进行社交网络链路预测。

算法1 描述了SE-ACO 算法的具体过程，其目的是由社交网络在时刻t的快照找出图1 中子图(a)与子图(b)，然后预测这些子图中在时刻t+1 的快照的潜在链接（即图1 中的虚线链接）。接下来，根据蚁群优化算法找出的社交网络中的三角关系。找到三角关系后，本文试图根据这些三角关系找出图1中的子图(a)与子图(b)。由于某些链接在多个子图结构中是共用的，故其评分会更高。最后，本文按评分降序排列得出预测链接的列表。

算法1SE-ACO 算法

输入三角关系triangles(G)

输出预测链接result ←result+link

3.2 基于改进蚁群优化算法定位三角关系的模型构建

为了找出三角关系，本文对蚁群优化算法进行了改进，与原始蚁群优化算法的区别主要有以下几点。

1) 假设初始状态下蚂蚁没有家，这表示所有蚂蚁在一开始时是分散在社交网络的各个节点中的。

2) 与原始蚁群优化算法（如式(1)所示）相反，SE-ACO 算法中的蚂蚁更倾向于选择信息素含量较低的路径。这一特性使蚂蚁能够有更高的概率对社交网络图上未曾勘探过的部分进行探索。蚂蚁k由节点i移动至节点j的概率如式(6)所示，其中，τ为对应边的信息素含量；α为基本参数，本文设α=1。与式(1)不同，即SE-ACO算法与传统蚁群优化算法的区别，式(6)令β=0，且其两者图中的信息素含量成反比。如果给释放的信息素一个负值系数，则蚂蚁移动与信息素之间为正相关关系。

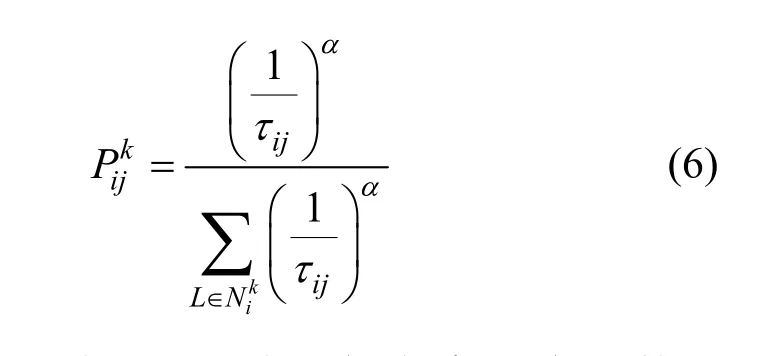
3) 食物（即解）呈现为三角关系，而蚂蚁的目标是找出三角关系。由于每个三角关系中都存在3 个节点，而蚂蚁拥有如图3 所示的特殊记忆力，故蚂蚁在社交网络图上的每次移动均会记录在其记忆中。如果记忆存在已满，则将数据写入先前的记忆单元内（图3 中数字表示蚂蚁循环覆盖的特殊记忆力，箭头代表循环覆盖的方向），但首先要检验准备写入的数据是否等同于先前的记忆单元，如果相等，则认为找到了三角关系。

图3 蚁群优化算法中蚂蚁的记忆结构图

4) 令所有边上的信息素的初始数量均等于一个单位，如果信息素属于已找出的三角关系中的边，则边上的信息素将增加。每当发现一个三角关系时，该三角关系中所有边上的信息素将增加一个单位，SE-ACO 算法中找到食物（即解）的方法为找出社交网络图中的三角关系。

5) 各边所释放的信息素不会消退。

6) 蚂蚁有死亡属性。鉴于该特性，蚂蚁不会勘探社交网络图中已访问过的部分，整个社交网络图都已被充分勘探后，由于不需要做进一步勘探，故所有蚂蚁都会死亡。蚂蚁死亡的条件如下：之前已勘探过的任意边均不含有初始信息素；困在2 个节点孤岛或边缘节点中；蚂蚁的周围环境都充满了信息素。

使用SE-ACO 算法进行三角关系查找的具体过程如算法2 所示。首先，创建一定数量的蚂蚁并将它们随机放置于社交网络节点中。由于蚂蚁会死亡，故蚂蚁的初始数量一般为社交网络图中节点数量的10～20 倍，且在移动2 次或3 次后，会有将近一半的蚂蚁死亡，而当所有蚂蚁死亡或迭代次数超过特定次数后，算法停止。在大多数网络中，算法2 的平均迭代次数为10。每次迭代时，新节点被蚂蚁选中的概率如式(6)所示，同时检查网络中是否发现新的三角关系，如发现则将该三角关系中所有边的信息素增加一个单位，然后将该三角关系加入已找到的三角关系列表中。每次迭代时均检查蚂蚁的健康状况，如果符合死亡条件中的任一条件，则该蚂蚁死亡。

算法2SE-ACO 算法寻找三角关系

输入初始化信息素initialize pheromone(E)

输出三角关系triangles(G)

Latany 等[33]在大型低权值网络中引入了一种新型三角计算算法，并使用Tsourakakis 等[34]所提特征三角形算法进行三角关系计算。刘树新等[35]所述三角计算方法的应用之一为链路预测，其理念为社交网络中朋友的朋友也是朋友的概率较大，故能生成最多三角关系的链接即是链路预测的最佳候选链接，这一理念与Newman 等[36]所提的公共邻点算法非常接近。由于链路预测不需要找出社交网络图中三角关系的确切数量，故Newman 等[36]所提的公共邻点算法并未找出社交网络图中三角关系的确切数量。要在大型社交网络图中找出三角关系的确切数量非常耗时，且成本很高。本文将改进蚁群优化算法用于查找三角关系，且将其应用于MapReduce 框架（一种高度并行的分布式大规模数据处理框架）中[37]，这提升了算法的可扩展性。如前所述，用于查找三角关系的所述方法的时间复杂度为O(n)。边上的信息素也可用于图形分区，这意味着信息素含量较低的边为图形分区的最佳候选点。而边上所释放的信息素也可用于确定节点的中心性，节点所连接的具有较多信息素的边越多，该节点的中心性越强[38]。

3.3 基于三角关系进行预测链接

本文根据上文中找出的三角关系来进行预测链接（如算法3 所示）。首先，确定已找出三角关系节点的所有邻点，然后检验每个邻居节点是否属于图1 中子图(a)或子图(b)中的一种。由于子图(b)优于子图(a)，因此如果社交网络图不是稀疏的，仅考察子图(b)就足够了。如果找出了一定数量的子图(a)或(b)，则这些子图中不存在的链接将被视为潜在链接。对于每个预测链接，可根据三角关系节点边上的信息素数量及它们所属的子图类型来计算其分数。信息素越高，则分数越高，子图(b)中的链接的分数较高。预测链接在某些子图结构间可能是重叠的，且要预测多次。每次进行一次链路预测，其分数就越高。2 个子图(b)之间的重叠链接如图4所示，由于该链接会预测2 次，故该链接的分数也较高。

算法3SE-ACO 算法的链路预测

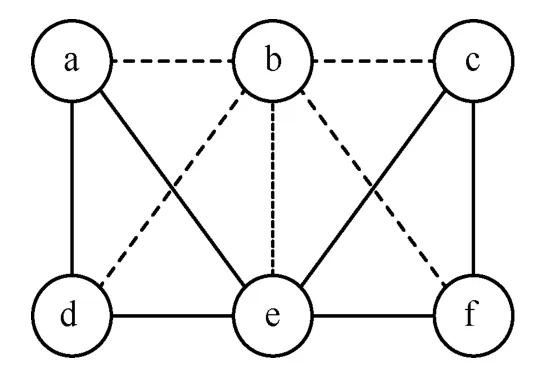
图4 2 个子图(b)之间的重叠链接

4 实验验证与结果分析

首先对数据集及其特征进行介绍，然后将SE-ACO 算法在这些数据集上的评估结果与其他非监督式结构链路预测算法进行比较。使用Top-n精度和接收器操作特性（ROC,receiver operating characteristic）曲线下面积及精确率−召回率曲线等方法进行评估，最后根据已执行的不同评估指标对算法结果进行了讨论。

4.1 数据说明

各数据集在时刻t和时刻t+1 的统计信息分别如表1 和表2 所示。SE-ACO 算法使用了时刻t的数据集来预测时刻t+1 的链接。其中节点和边的数量表示社交网络图中存在多少个节点和边，平均聚类系数表示三元组变成三角关系的倾向性度量，网络的聚类系数越高每个图中生成的链接越多。相称系数[39]是进行相似性度量的关键参数，度数相同的节点比其他节点更容易彼此关联，该度量范围为[−1,1]。相较于相称系数接近−1 的网络，在相称系数接近1 的网络中度数相同的节点彼此的关联度最高。强连通分量（SCC,strongly connected component）表示社交网络图中的子图，由于大型网络的直径计算非常耗时，故本文使用Lichtenwalter 等[40]中的近似算法来估算网络直径，使用五折交叉验证法来评估所提架构的性能。使用Rapidminer 数据挖掘工具随机选取各用户评级数据的20%作为测试集，并将剩余80%的用户数据作为训练集。

表1 各数据集在时刻t 的统计信息

表2 各数据集在时刻t+1 的统计信息

本文使用国内外共9 个相关数据集对SE-ACO算法进行验证，并利用Python 工具从新浪微博、Twitter 与Facebook 的AP（Iapplication programming interface）端口选取10 个节点作为初始节点，爬取真实用户数据集作为实验仿真的基础数据，爬取时间为2019 年1 月1 日—6 月30 日，数据集分别包含37 864 个新浪微博节点、49 822 个Twitter 节点和38 942 个Facebook 节点，记为时刻t；爬取时间为2019 年7 月1 日—12 月31 日，数据集分别包含42 093 个新浪微博节点、55 891 个Twitter 节点和42 965 个Facebook 节点，记为时刻t+1。除此之外，本文认为如果科研论文作者的合作网络、网站之间的信息分享网络与专利合作网络等都应纳入考察范围。但由于数据的可得性问题，故本文使用以下数据集进行分析。hep-ph 与astro-ph 表示科研论文作者合作网络，其中，hep-ph 为物理现象学领域，astro-ph 为天体物理学领域[2]。2004 年— 2006 年撰写论文的样本为时刻t，2007 年—2009 年撰写的论文的样本为时刻t+1。对上述2 个数据集，本文仅使用核图，且使用撰写3 篇论文及以上的作者作为节点。dblp-collab 和dblp-cite 均来自于DBLP 计算机科学文献[17]。其中，dblp-collab 为计算机科学作者合作网络，该网络中的时刻t为2001 年— 2003 年的作者合作，快照时刻t+1 为2004 年—2005 年的作者合作；dblp-cite 表示相互引用的计算科学论文网络，该网络的时刻t为1997 年—1998 年，时刻t+1 为1999年—2000 年。Polblogs 为2004 年的美国政治网络及网站间的链接[41]，将该网络图中的后20%划分为时刻t+1，其余则为时刻t。patent-colla 为节点为专利作者的数据集，其链接表示专利作者间的合作[42]。时刻t为2006 年—2007 年作者的合作，时刻t+1为2008 年—2009 年的合作，并将所有数据以csv格式保存在MySQL 数据库中以便进行数据处理。对每一个社交网络数据集，采用80%的数据进行训练，剩余的20%用于测试。

4.2 实验结果

为体现SE-ACO 算法的优越性，本文将其与10 种不同的非监督式结构链路预测算法进行了对比。这10 种算法的简要描述如下。

1) 公共邻点（CN,common neighbor）。令Γ(x)表示节点x的邻点数，2 个领点具有的公共邻点越多，则链路预测任务[36]的分数越高，如式(7)所示。

2) AA（Adamic-Adar）算法。Adamic 等[41]设计了一种用于检测2 个网页相似度的度量，这种度量也可用于度量社交网络中两节点的相似度，具体如式(8)所示。其中，文献表明度数较小的2 个节点的公共邻点比其他节点更有价值。

3) Jaccard 系数算法。该相似度度量类似于寻找公共邻点，不同之处在于，就此度量方法而言，如果2 个节点有较多的公共邻点和较少的非公共邻点，则它们的相似度较大[8]，如式(9)所示。

4) 优先连接（PA,preferential attachment）算法。节点度数是预测新链接的关键属性。度数较高的2 个节点在未来彼此交互的可能性越大[9-11]，这一理论可由式(10)推导得出。

5) Katz（Katz 指数）算法。该度量根据两节点之间的路径数及其长度来确定节点之间的相似度[43]，如式(11)所示。

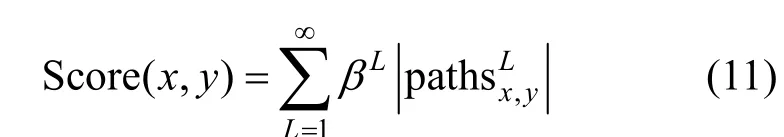
6) Distance（距离）算法。使用距离算法进行相似度度量时，距离越近的两节点关联的机会越高，因此，距离2 个跳点的节点，其彼此关联的概率最大[3]。在该度量算法中，距源节点具有相同数量跳点的节点与源节点形成的链接都具有相同的打分。

7) RP（Rooted PageRank）算法。该算法基于随机游走，由PageRank[44]算法改写而成，并被文献[2]用于链路预测，如式(12)所示。其中，Hx,y（节点x,y的首次接触时间）为随机游走者由节点x移动至节点y所需的步数。由于击中时间不对称，因此Hy,x的首次接触时间也是不同的。式(12)中的πx与πy均为平稳概率，为防止随机游走者距离起始节点x太远，这里使用了概率α，即随机游走者返回至起始节点的概率为α，移动至邻点的概率为1−α。本文实验设α=0.5。

8) SR（SimRank）算法。在该相似度度量算法中，2 个节点越相似，则分数越高。该算法的主要思想是根据社交网络的趋同性[11]进行预测。SimRank算法[45]可由式(13)～式(15)表示，如果2 个节点与较多的相似节点有关联，则这2 个结果较相似。式(14)中的γ取值为[0,1]，本文实验中，设γ=0.8。

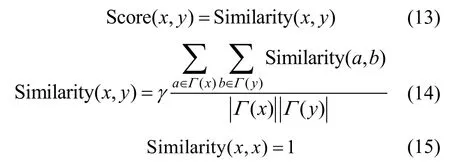
9) PF（PropFlow）算法[46]。该算法为一种限制性随机游走预测器，是横向优先搜索的变形，本文实验中仅考虑了最大长度为5 的路径。

10) 资源分配（RA,resource allocation）算法。该算法是基于复杂网络中的资源分析理念提出的[4]。其中，节点x可借助于邻点向节点y发送资源。简化情况下，每个节点仅向目标节点发送一个单位的资源，且该资源将发送至该节点的所有邻节点。节点x和y的相似度为它从节点x所得到的资源数量。参考文献[4]中的做法，使用式(16)中的deg(z)表示节点z的度数。

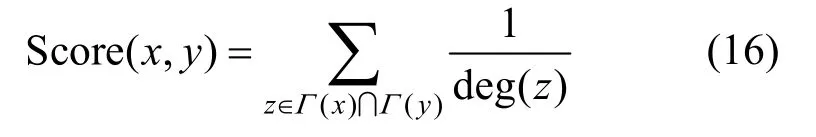
本文在Python 环境中分别使用Scipy[47]、Numpy[48]和LPmade 工具包[40]执行上述算法。用于计算链接精度和召回率的真正例（TP,true positive）、真负例（TN,true negative）、假正例（FP,false positive）和假负例（FN,false negative）的定义如表3 所示。而召回率（Recall）、精确率（Precision）、真正率（TPR,true positive rate）和假正率（FPR,false positive rate）分别如式(17)～式(20)所示。

表3 链路预测中TP、TN、FP 和FN 的定义

根据文献[3]进行第一次评估，将每个算法的精度与随机预测器的精度进行比较，其中随机预测器的精度为图形时刻t+1 所创建新链接的数量除以图形时刻t消失链接的数量。每个数据集中随机预测器的精度如表4 所示。该指标也称为Top-n精度，其中n表示时刻t节点之间增加的新链接。在本文实验中，所有算法都进行了100 次迭代实验，并取平均值作为预测精度的实验结果，且各组方差的分布区间为[1.033,3.784]。

根据优于随机预测器的倍数，SE-ACO 算法的Top-n与其他算法的精度比较情况如表5 所示，n为大于或等于1 的正整数，精度会随n先变大再变小。对于每个预测器，给定数字表示优于随机预测器的倍数。例如新浪微博数据集上SE-ACO 算法的结果为42.68，这表明该算法的精度要优于随机预测器42.68 倍，因此SE-ACO 算法在新浪微博中的精度为24.69%，即0.578 4%与42.68 的乘积。表5中的SR 和RP 用于大型数据库时非常耗时，故使用少数数据集进行实验时未使用这些算法。对于Twitter 数据集的实验结果中AA 预测器效果最佳的原因，本文认为这是由于AA 预测器为基于节点相似度进行预测的，其中度数较小的2 个节点的公共邻点比其他节点更有价值。而由于Twitter 为主要发布短文本的社交网络平台，故节点之间相似度本身较强，预测精度相对较高。

本文实验中，由于使用SE-ACO 算法预测列表在每次运行时都有可能不同，故设置评估结果为迭代100 次运行后的平均值，运行结果的标准差为1.328。SE-ACO 算法考虑了图1 中的子图(a)与子图(b)。

蚂蚁的初始数量取决于图的节点数，如果蚂蚁数量不足，则所找到三角关系可能较少，从而降低了SE-ACO 算法的评估结果。实验表明，当蚂蚁的初始数量设定为网络节点数的 10～20 倍时，SE-ACO 算法的运行效率最佳。本文实验将蚂蚁的初始数量设为各数据集节点数的10 倍。为进一步比较算法的可扩展性，本文比较了不同网络中基于节点数量的算法的运行时间，如图5 所示。由图5可知，运行效率最高的算法为CN 算法，而SE-ACO算法的运行时间接近CN 算法，这表明它可用于大型数据集的预测。且各预测器在不同数据集的表现基本一致，故在此不再赘述。

表4 几种算法在数据集的精度对比

其他评估方法为ROC 面积[49]和精确率−召回率曲线方法[50]。各算法根据ROC 曲线下面积的评估结果如表6 所示；新浪微博、hep-ph 和patent-colla数据集根据精确率−召回率曲线下面积所得的评估结果如表7 所示。ROC 曲线如图6(a)～图6(c)所示，所选的3 个链路预测算法在3 个数据集上的精确率−召回率曲线如图6(d)～图6(f)所示。结果表明，在大多数预测器中SE-ACO 算法的精度都高于其他算法，而预测器在某几个数据集中精度较低的原因是由于数据集本身特征所导致（其他预测器实验所得结果在此不再赘述）。

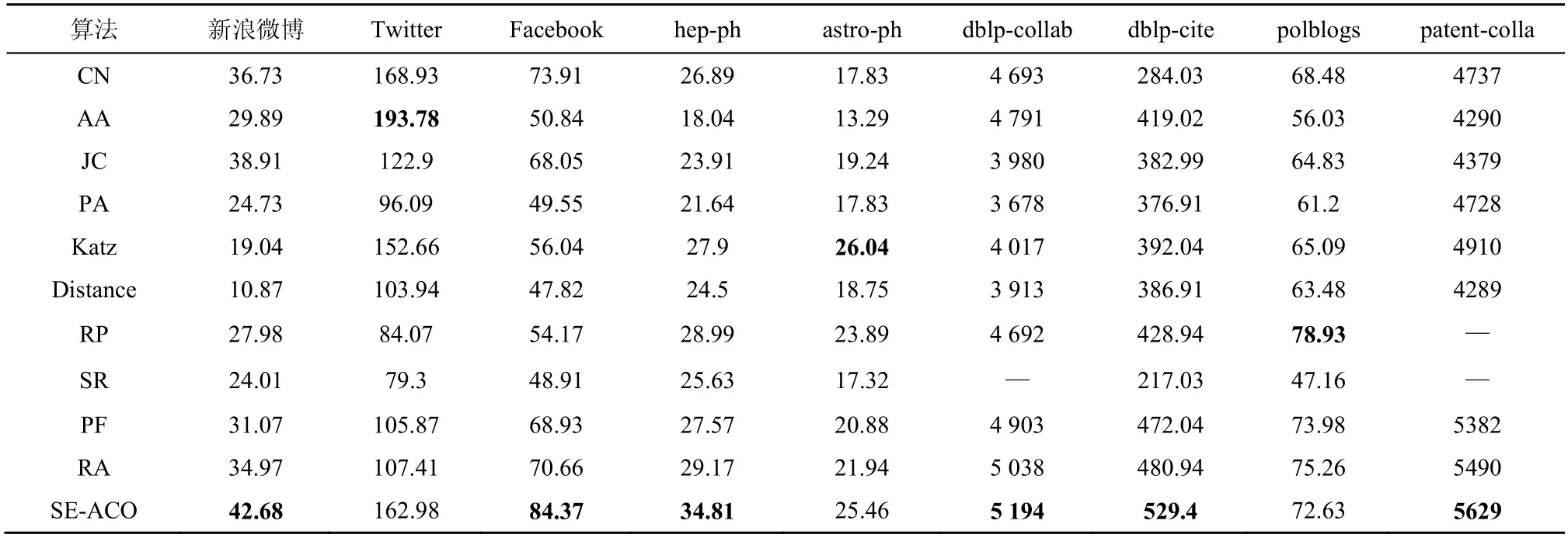
表5 SE-ACO 算法的Top-n 与其他算法的精度比较情况

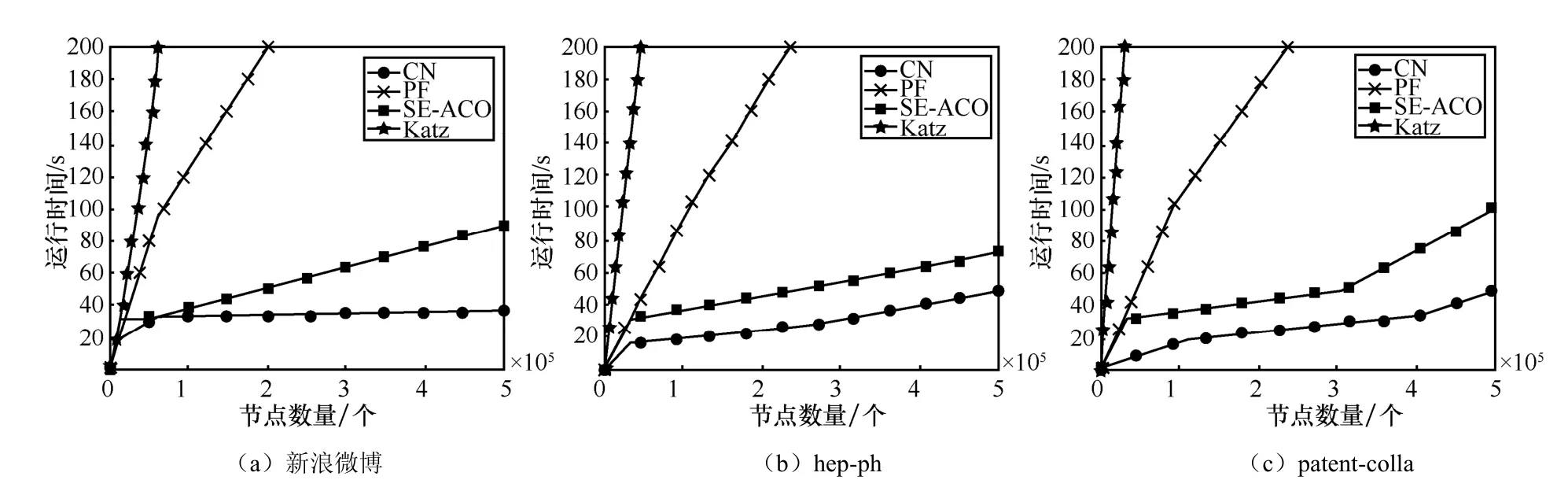
图5 算法运行时间对比

表6 基于ROC 曲线下面积的不同算法比较

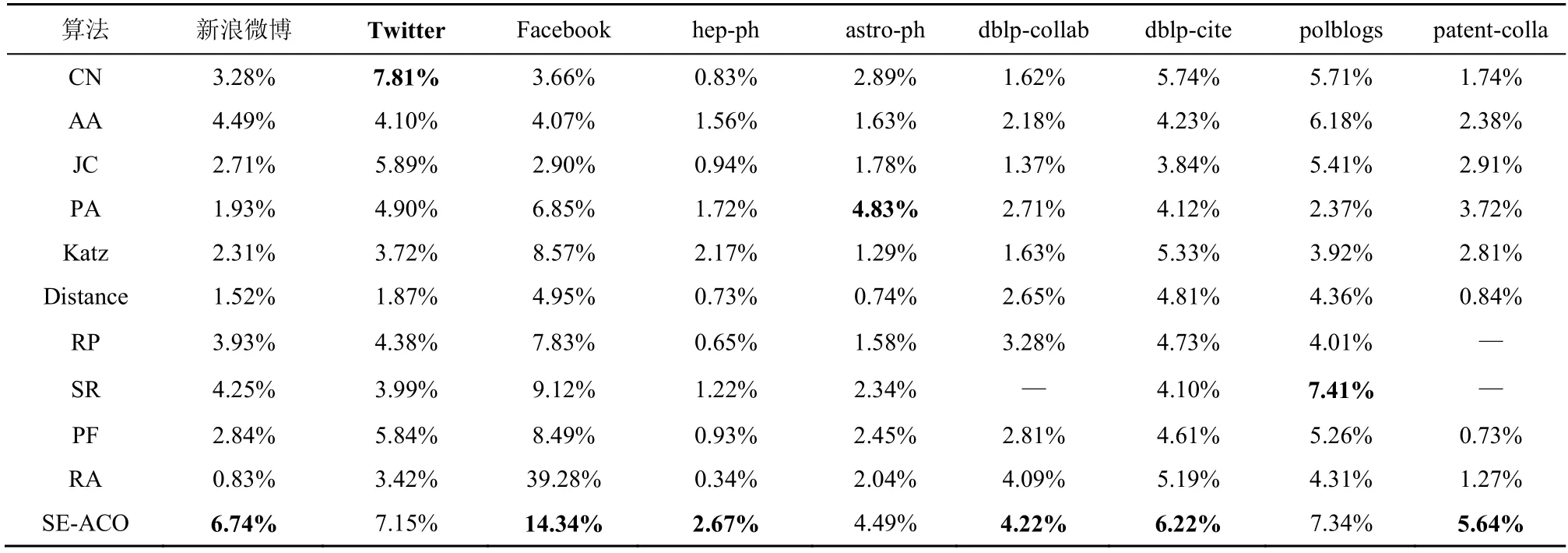
表7 基于精确率−召回率曲线下面积的不同算法比较

图6 基于ROC 与精确率–召回率曲线的算法比较结果

表4 表明可用随机链路预测器的性能评估链路预测算法的总体性能，即如果随机预测器在某些网络上表现良好，则链路预测算法在该网络上的性能也较好。另一方面，随机预测器在聚类系数较高、密度较高且图形直径较短的网络上的性能较好（如表2 所示）。Katz 指数性能取决于网络直径，即在直径较短的网络中，该算法有着更好的Top-n精度（如表2 和表5 所示）。AA 算法与CN 算法均使用了公共节点数来测量相似度，但AA 算法几乎在所有数据集上均优于CN 算法。AA 算法在聚类系数较高的网络中有着较好的性能，其原因是在这些算法中，能将更多的三元组转化为三角关系的链接为价值较高的链接，其得分也较高（如表2 和表6 所示）。SE-ACO 算法在 dblp-collab、dblp-cite 和patent-collab 数据集上的结果较好，其主要原因为该数据集的SCC 值较高，因此使用节点度数和路径长度方法的性能较低。在SE-ACO 算法中，蚂蚁开始时是随机分散在社交网络的各个部分，更多地利用网络的结构特性，因此SE-ACO 算法在出度较高的网络上有着较好的性能。图6 表示SE-ACO 算法的链路预测精度较高，这是由于根据图1 中子图(b)所预测的链接有较高的分数，这些链接位于预测列表的顶部，但根据子图(a)所预测的结果则较差。表6 中的Distance 算法在所有数据集上所得结果均一致，这是因为该算法将它预测的所有链接都关联了相同的分数。最后本文将表5 与表7 中的结果进行对比可知，如果这些算法用Top-n精度得出的性能较好，则其用精确度–召回率曲线下面积所得出的性能也较好。

为评估SE-ACO 算法在大型公开标准数据集中的性能，本文选择了3 个数据集：MovieLens 1M、MovieLens 10M 基准数据集[51]和Epinion 数据集[52]，结果如图7 所示。由图7 可知，在大型公开标准数据集中，SE-ACO 算法较其他算法仍然可以得到较高的精度，这也再次证明了SE-ACO 算法的科学性。

图7 公开标准数据集中基于ROC 曲线下面积的几种算法的比较结果

5 结束语

本文提出了一种基于子图演化与改进蚁群优化算法的社交网络链路预测方法。首先在社交网络图中确定特殊子图；然后研究子图演化以预测图中的新链接，并用蚁群优化算法定位特殊子图；最后本文针对SE-ACO 算法使用不同网络拓扑环境与数据集进行检验与算法比较。实验结论表明，与其他无监督社交网络预测算法相比，SE-ACO 算法在多数数据集上的评估结果最好，这表明图形结构在链路预测算法中起到重要作用。SE-ACO 算法在大型公开标准数据集上的运行时间较短且效果较佳。通过使用SE-ACO 算法，能以高度并行方式进行链路预测。

本文可以从以下几个方面进一步展开研究。1)由于数据可得性，本文与众多文献[7,44]一样，采用若干个社交网络数据集进行实验，这些数据集往往具有不同的量级，这会在一定程度上影响实验结果[45]。因此，在未来的研究中，有必要使用不同场景、不同量级的数据集来进行社交网络中的链路预测实验。2) 本文仅包含图1 所示的2 种子图结构，未来可以尝试使用更复杂的子图结构进行算法改进，这能够使链路预测算法适合更多的社交网络场景。3) 未来可以进一步融入其他机器学习和深度学习方法进行算法改进。