基于峭度原则的EEMD-MCKD的柔性薄壁轴承故障特征提取
刘兴教, 赵学智, 李伟光, 陈 辉
(华南理工大学 机械与汽车工程学院, 广州 510640)
柔性薄壁轴承作为谐波减速器的核心零部件之一,其工作的稳定性决定了谐波减速器的性能[1]。柔性薄壁轴承装配在谐波减速器后被强制变形为椭圆,运行过程中内、外圈受到椭圆长短轴周期性的径向作用力[2]。与普通滚动轴承相比,柔性薄壁轴承受到的冲击可分为两种,一种是椭圆长短轴交替产生的冲击,另一种是由于故障导致零件之间相互接触产生的冲击[3]。且由于柔性薄壁轴承工作时为椭圆形,变化的节径导致柔性薄壁轴承的故障特征频率为某一区间范围内变动的值[4-5]。因此,相对于普通滚动轴承,柔性薄壁轴承的振动信号更为复杂,故障特征提取更加困难。
Huang等[6]在1998年提出一种自适应的时频分析方法——经验模态分解(Empirical Mode Decomposition,EMD),无需先验基函数,能将非线性非稳态信号分解成一系列固有模态分量(Intrinsic Mode Function, IMF),并且已成功应用在不同领域的信号特征提取中。然而,EMD算法的有效性受模态混叠的影响,为了克服这一缺陷,Huang等[7]提出一种噪声辅助的EMD算法,集成经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)。在各领域应用广泛,例如,王志坚等[8]使用最小熵反褶积(Minimum Entropy Deconvolution, MED)与EEMD相结合的方法对滚动轴承温柔故障特征提取进行了研究。沈长青等[9]提出基于EEMD和改进的形态滤波方法,对周期性脉冲成分进行提取。
最大相关峭度解卷积方法(Maximum Correlated Kurtosis Deconvolution, MCKD)是McDonald等[10]对MED进行改进时提出的。以滤波后信号的相关峭度为目标函数,求解最优解卷积滤波器参数。由于MCKD算法具有强噪声背景信号特征提取的能力[11],其在信号检测领域已经获得了非常广泛的应用。例如何玉灵等[12]利用MCKD算法对发电机振动信号进行故障特征提取,唐道龙等[13]利用相关峭度实现了强噪声背景下的行星齿轮振动信号微弱故障特征的提取,唐贵基等[14]利用最大相关峭度解卷积结合1.5维谱对滚动轴承早期故障特征进行了提取。虽然MCKD算法已在轴承故障特征提取上取得了良好的应用效果,但对于柔性薄壁轴承这一复杂背景下的轴承故障信号的应用,目前仍鲜有研究。
为将柔性薄壁轴承故障冲击信号从复杂的背景成分中提取出来,提出基于EEMD-MCKD的柔性薄壁轴承故障特征提取方法。首先使用EEMD对信号进行预处理,选用峭度原则滤除信号中的无关分量和冗余分量,重构筛选后的IMF得到EEMD提纯信号。然后使用针对柔性薄壁轴承进行过参数优化的MCKD算法对EEMD重构信号进行提取。运用此方法对实测柔性薄壁轴承外圈故障振动信号进行特征提取,结果表明准确提取到了清晰的故障特征频率。并将提取效果与单一EEMD算法和MCKD算法进行对比分析。
1 相关理论
1.1 柔性薄壁轴承故障振动信号特征频率计算
柔性薄壁轴承装配到椭圆轴后,其内外圈为椭圆,故障特征频率和普通滚动轴承完全不同,对于外圈损伤,柔性薄壁轴承的故障特征频率可用下式表示
(1)
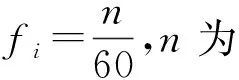
(2)
式中:θ为逆时针方向与x轴的夹角;a为椭圆短轴;b为椭圆长轴。
由式(1)可见,由于椭圆轴旋转过程中w时刻发生变化,因此,柔性薄壁轴承的故障特征频率ffault具有时变特性。另外,由于实际实验信号中测得的转速存在误差,因此将解卷积周期范围扩展,得Tfc
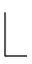
(3)
式中:

为向下取整,

为向上取整;Tf=1/ffault为故障特征周期。
1.2 集成经验模态分解
EMD的主要缺陷是会产生模态混叠,即一个固有模态分量(IMF)含有多个频率成分。为解决这一问题,Wu和Huang提出基于噪声的EMD算法——集成经验模态分解(EEMD),它比标准EMD方法具有更好的尺度分离能力。EEMD通过多次向信号中添加不同的白噪声,每次都对加噪信号进行EMD处理,最后对相关的IMF进行总体平均来消除加入噪声的影响,以改善EMD的模态混叠。EEMD算法的步骤如下:
步骤1在给定的信号x(t)中加入白噪声序列un(t)得到一个新的时间序列Yn(t)=x(t)+un(t),n=1,2,…,N,n为加入白噪声的次数,总共N次。
步骤2基于EMD算法,加入噪声的信号Yn(t)分解为IMF和残余分量。
(4)
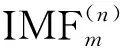
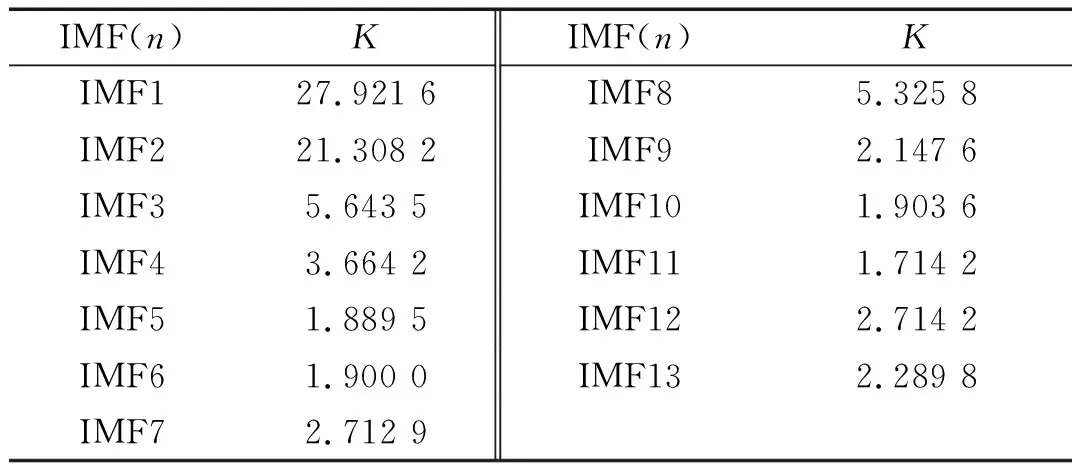
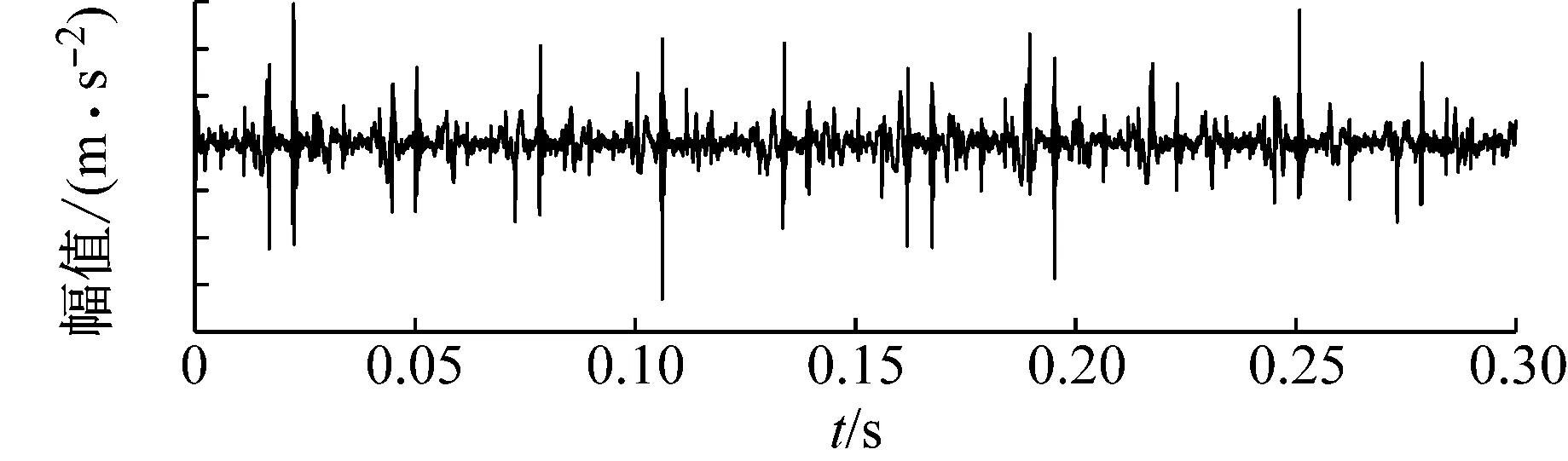
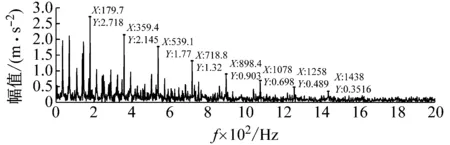
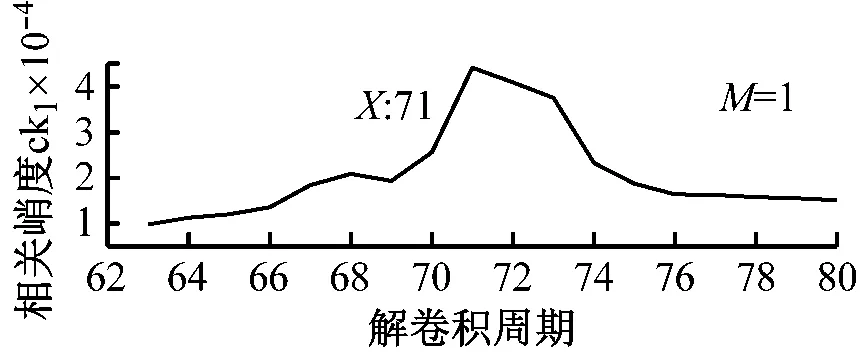
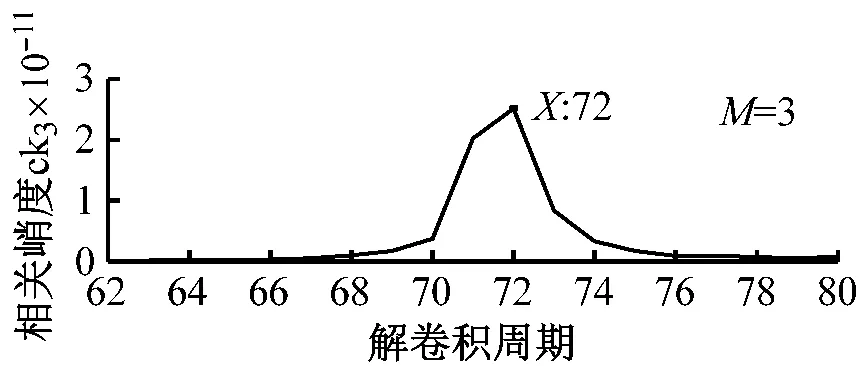
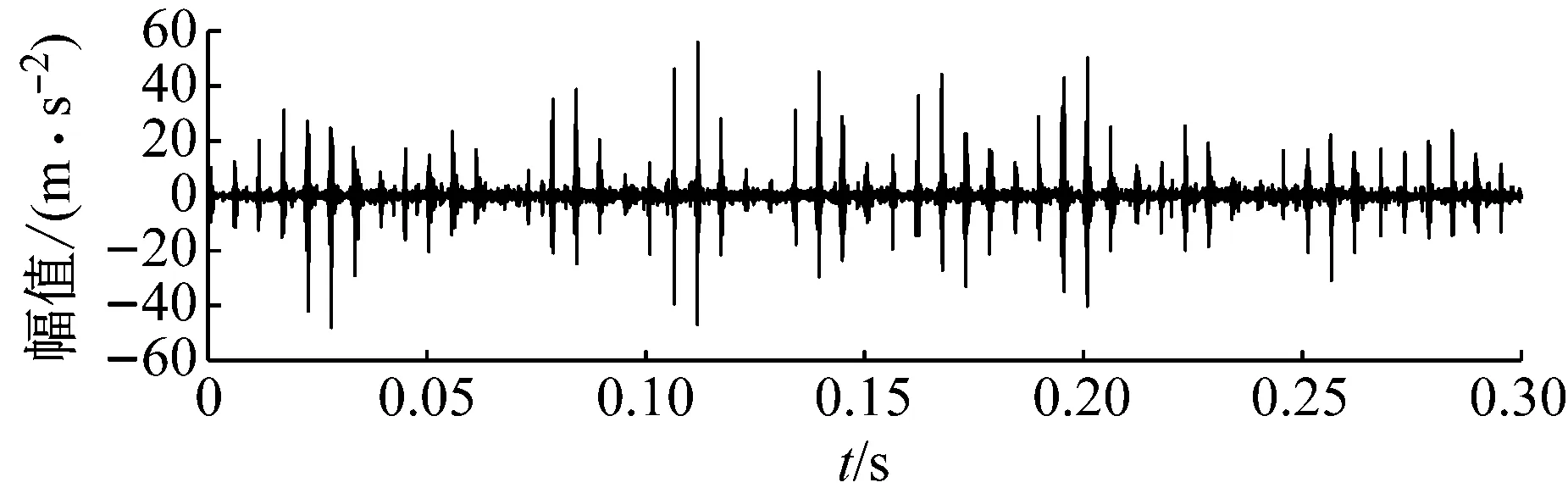
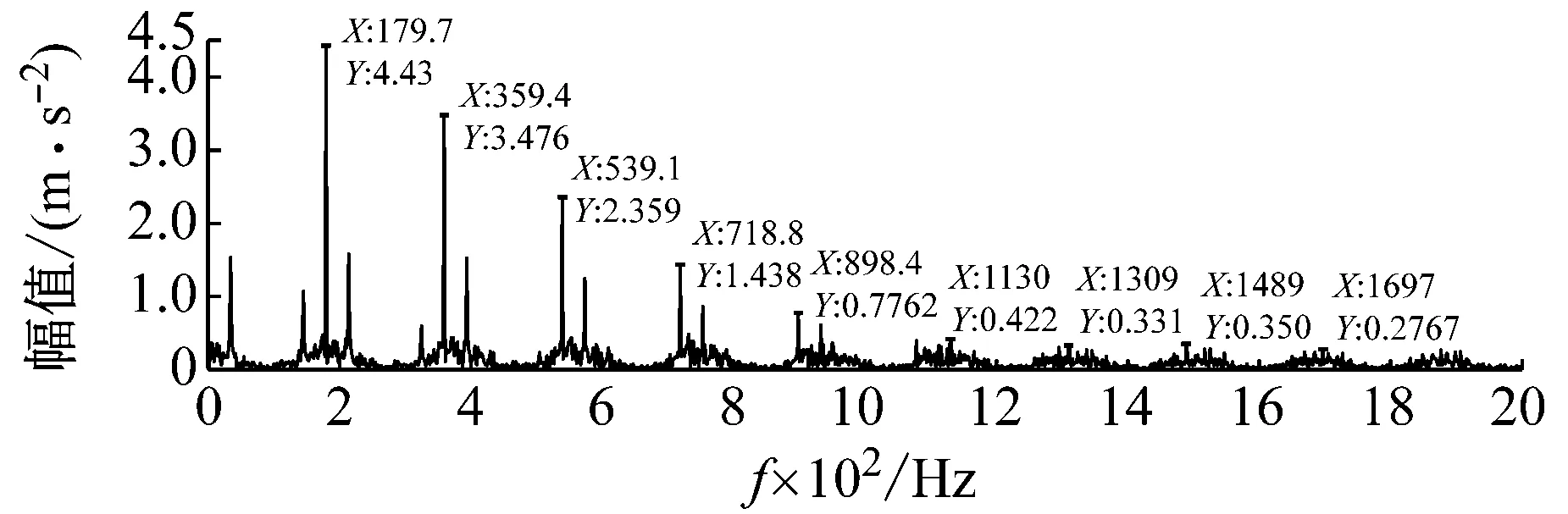
步骤3判断n 步骤4通过对N次试验中的m个IMF取平均,得到最终的固有模态分量IMF (5) EEMD的结果取决于试验数目(N)和加入的噪声幅值(A),N和A应满足如下关系[15] (6) 式中,ε为误差的最终标准偏差,即原始信号与EEMD产生的IMF之和之间的差值。 本文添加噪声序列的标准差等于0.2乘以原始数据的标准差,实验次数设为N=100。 使用峭度准则对分解的IMF进行筛选,峭度值K的表达式为 (7) 式中:E(t)为变量t的期望值;μ、σ分别为信号x的均值和标准差。当IMF的K>3时,说明该分量中含有较多冲击成分。选取所有峭度值大于3的IMF进行重构,可以滤除原信号的冗余成分,故障表现的越明显。 MCKD将相关峭度的最大化作为寻优原则,通过迭代确定最优的滤波器f来从传感器获得的振动信号中提取出故障冲击成分,能够提取信号中的周期性故障特征、消除由于复合故障耦合出现的频率交叉现象[16]。 相关峭度的定义如下 (8) 式中:M为位移数;N为输入信号的长度;T为解卷积周期,由振动信号中故障特征频率ffault和采样频率fs决定。 (9) 式中,yn为输出信号,可表示为 (10) 式中:xn为输入信号;f,L分别为滤波器系数和滤波长度。 MCKD算法的目标函数为 (11) 由式(10)和式(11)可得滤波器系数的迭代表达式为 (12) 根据式(12)计算的滤波器系数代入式(10),可以提取到解卷积信号y。 MCKD算法受滤波器长度L、解卷积周期T、位移数M和迭代次数N等参数的影响,取式(3)计算出的Tfc的各个值对信号x进行相关峭度计算,根据相关峭度最大值确定解卷积周期T。具体实现可按以下步骤进行: 步骤1位移数M取值为1,根据式(1)、式(2)、式(3)确定Tfc; 步骤2计算Tfc中各个值对应信号的M位移数相关峭度值得到ckM。对ckM序列从大到小排序,得到一个新序列ck_sort; 步骤3若ck_sort序列中的第一个值大于第二个值的3倍,则根据ckM中最大相关峭度值所在位置确定最佳的解卷积周期T,算法结束。否则M=M+1,转至步骤2,循环直至算法结束。 根据确定的解卷积周期T,取位移数M=1,滤波器长度L取值范围为[16,256],根据滤波后信号的相关峭度值ck1来选择合适的滤波器长度。 最后令M=1:7,计算不同M取值,由相关峭度值最大原则确定最佳位移数M,根据确定的参数进行MCKD滤波,一般M取1即可。 总结以上分析,得到MCKD算法故障诊断流程如图1所示。 柔性薄壁轴承运行过程中内、外圈受到椭圆长短轴周期性的径向作用力。与普通滚动轴承相比,柔性薄壁轴承受到的冲击除了故障导致的周期性冲击外,还有椭圆长短轴交替产生的周期性冲击。因此,相对于普通滚动轴承,柔性薄壁轴承的振动信号更为复杂。 EEMD方法可以根据原始信号的振动特征,将其分解为一系列固有模态分量(IMF),滤除残余IMF分量,可以有效地将信号中的噪声背景成分分离出来。由于使用EEMD方法处理过的信号信噪比更高,因此,相比于直接使用MCKD方法处理原始信号,能够将柔性薄壁轴承的故障冲击反映得更明显。基于EEMD-MCKD的柔性薄壁轴承故障特征提取流程如图2所示。 图1 MCKD算法的柔性薄壁轴承故障特征提取流程 图2 基于EEMD-MCKD的柔性薄壁轴承故障特征提取流程 如图3所示,在柔性薄壁轴承测试平台上对故障柔性薄壁轴承的振动信号进行采集。试验台信号采集系统由PCB加速度传感器、LMS SCADAS数据采集系统组成,如图4所示。本文试验用柔性薄壁轴承与普通轴承结构对比图如图5所示,可以看出,相对于普通轴承而言,柔性薄壁轴承的内、外圈很薄,装配到椭圆轴上后内、外圈会发生强制变形变成椭圆。 图3 柔性薄壁轴承测试平台 图4 LMS软硬件信号采集系统 (a) 普通深沟球轴承 (b) 柔性薄壁轴承 表1为所用柔性薄壁轴承的基本尺寸参数。在振动信号采集时,主轴转速为1 050 r/min,径向载荷为200 N,振动信号采样频率为12 800 Hz。其正常柔性薄壁轴承振动信号时域波形如图6(a)所示,其频谱图如图6(b)。可见信号中存在明显的周期性冲击,这是由柔性薄壁轴承变为椭圆形后的长短轴交替产生的冲击。 表1 柔性薄壁轴承参数表 外圈损伤柔性薄壁轴承如图7所示,对此柔性薄壁轴承在实验台上进行振动检测。得到其振动时域波形如图8(a)所示,其频谱图如图8(b)。从图8(a)可以看出有明显的冲击成分,但周期性不明显。从图8(b)可以看出幅值较大的谱线集中分布在0~400 Hz,在高频段内为幅值几乎为0。 (a) 时域波形图 (b) 频谱图 图7 外圈故障柔性薄壁轴承 (a) 时域波形 (b) 频谱图 对图8所示的外圈故障柔性薄壁轴承振动信号利用EEMD方法进行分解,设置加入的噪声幅值与信号幅值的标准差之比ε=0.2,试验次数N=100,得到分解后的IMF波形如图9所示。 (a) IMF1 (b) IMF2 (c) IMF3 (d) IMF4 (e) IMF5 (f) IMF6 (g) IMF7 (h) IMF8 (i) IMF9 (j) IMF10 (k) IMF11 (l) IMF12 (m) IMF13 从图9可以看出:各阶固有模态分量的幅值随着阶数的增大而减小;IMF1、IMF2、IMF3、IMF4有明显冲击成分;IMF5虽然也有冲击成分,但幅值远小于前4阶;IMF6-IMF11幅值相比前5阶小很多,且无明显冲击成分,可以判断为残余分量。 采用峭度原则对EEMD分解得到的IMF分量进行挑选,选取峭度值K大于3的固有模态分量,计算各IMF的峭度值如表2所示。综合考虑峭度和幅值,选择IMF1、IMF2、IMF3、IMF4进行重组,提取的外圈故障柔性薄壁轴承振动特征时域信号如图10(a),包络谱如图10(b)所示。 表2 各阶模态分量峭度值 从图10(b)可以看出,使用EEMD方法对原始信号进行处理,不仅冲击成分相比图8(b)更加明显,而且还可以看出轴承外圈的故障频率及倍频成分。然而,包络谱图中的[0,200]Hz频率段冲击幅值较高,且基频和各倍频附近的边频没有得到很好的抑制,依然很难对轴承的故障特征做出判断。 对图10的重构信号采用MCKD方法进行处理。将表1的参数代入式(1)、式(2)、式(3),得到Tfc=[63,80],确定解卷积周期T的范围为[63,80]。 (a) 时域波形 (b) 包络谱图 按照图1的流程从[63,80]中选取最优的T值。不同解卷积周期下原始振动信号的相关峭度值如图11所示,可见M取值为1、解卷积周期T=71时,相关峭度值最大。 图11 不同解卷积周期下原始振动信号的相关峭度值 取位移数M=1、解卷积周期T=71,取滤波器长度L=16,并依次递增一直取到L=256,分别采用MCKD算法进行滤波,得到对应滤波后信号的相关峭度以及计算时间如图12所示。从图中可以看出,随着滤波器长度的增加,MCKD滤波后的信号的相关峭度值越大,但相关峭度在滤波器长度大于158后,相关峭度基本不变。因此,出于算法精度以及时间效率的考虑,确定滤波器的长度L为158。 在位移数M=1、解卷积周期T=71、滤波器长度L=158这三个参数下,对EEMD重构信号进行特征提取,结果如图13所示,可见在时域中提取到了周期性的冲击。从包络谱图可以看出,这种冲击是以179.7Hz为基频的一系列高次倍频组成。根据式(2)和式(3)可以算得,外圈损伤特征频率的最大值是187.0 Hz、最小值是172.5 Hz、其平均值是179.75 Hz,这与179.7 Hz非常接近,这说明179.7 Hz就是外圈损伤的特征频率,因此,柔性薄壁轴承外圈故障特征就被提取出来了。 图12 不同滤波器长度下MCKD算法计算时间以及滤波后信号的相关峭度对比图 (a) 时域波形 (b) 包络谱图 与EEMD处理得到的包络谱图(见图10(b))相比,可以发现,使用优化参数后的MCKD算法对EEMD重构的信号提取,除了可以明显看出冲击成分,[0,179.7]Hz频率段的幅值几乎为0,基频和各倍频附近的边频也得到了很好的抑制,可以很容易对轴承的故障特征做出判断。 为了证明EEMD与MCKD相结合在柔性薄壁轴承故障振动信号提取上的优越性,将EEMD-MCKD算法与单一MCKD算法的提取效果进行对比分析。在相同滤波器长度和相同位移数下,使用MCKD算法直接对柔性薄壁轴承外圈故障特征进行提取,其时域信号如图14(a)所示,包络谱如图14(b)所示。 (a) 时域波形 (b) 包络谱图 从图14(b)可以看到,单一MCKD算法处理后的振动信号包络谱基频下的幅值为4.31,而从图13(b)可以看到,EEMD-MCKD提取结果为4.61,幅值比MCKD算法提取到的高出0.3。此外,相同倍频下,MCKD算法提取到的信号包络谱幅值均低于EEMD-MCKD算法。 在EEMD-MCKD算法中,由于EEMD对故障信号进行了提纯,过滤掉了信号中的无关分量和冗余分量,将剩下的IMF分量进行重构,这样,重构的信号中故障振动成分能量就得到了提升,再使用MCKD算法提取冲击的信号,得到的特征包络谱中故障特征频率幅值就会有所提高。因此对于本文中的外圈故障柔性薄壁轴承振动特征提取来说,EEMD-MCKD算法的提取效果更佳。 本文分析了柔性薄壁轴承振动信号特点,提出基于峭度原则的EEMD-MCKD的柔性薄壁轴承故障特征提取方法。该方法将EEMD算法与MCKD算法相结合,发挥了两种算法各自的优势,同时又克服了两种算法在柔性薄壁轴承故障特征提取中的局限性。 将基于峭度原则的EEMD-MCKD算法对实测柔性薄壁轴承外圈故障振动信号进行故障特征提取,可以准确提取到故障特征频率。并将提取效果与单一EEMD算法和MCKD算法进行对比分析,结果表明,基于峭度原则的EEMD-MCKD算法提取的故障特征频率的幅值更大,提取效果更佳。1.3 最大相关峭度解卷积
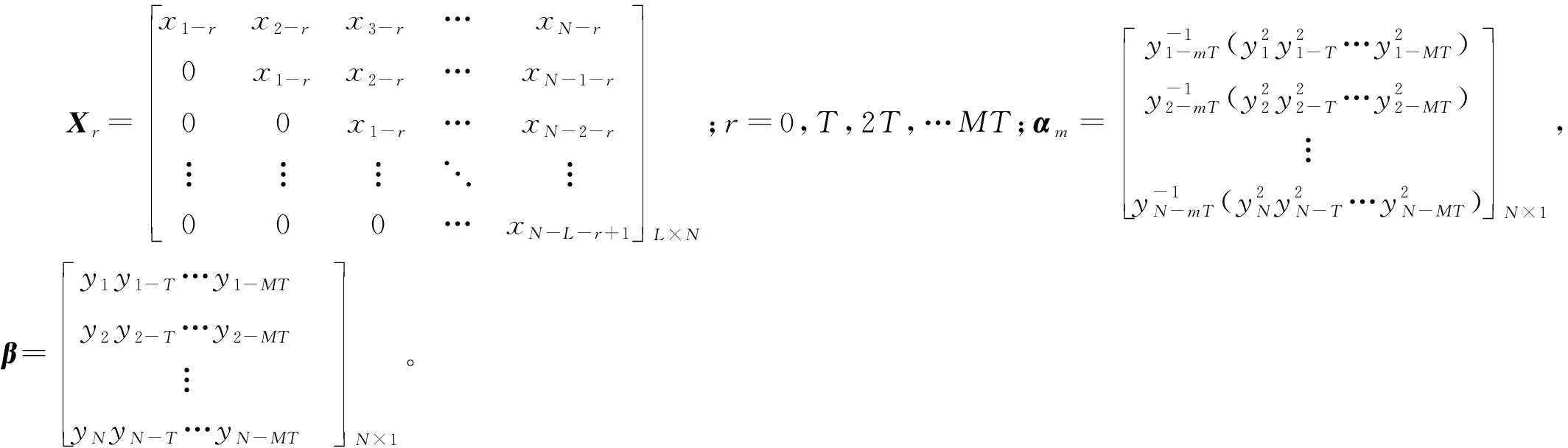
2 基于EEMD-MCKD故障特征频率提取方法
2.1 MCKD参数选择分析及特征提取流程
2.2 EEMD-MCKD的柔性薄壁轴承故障特征提取方法
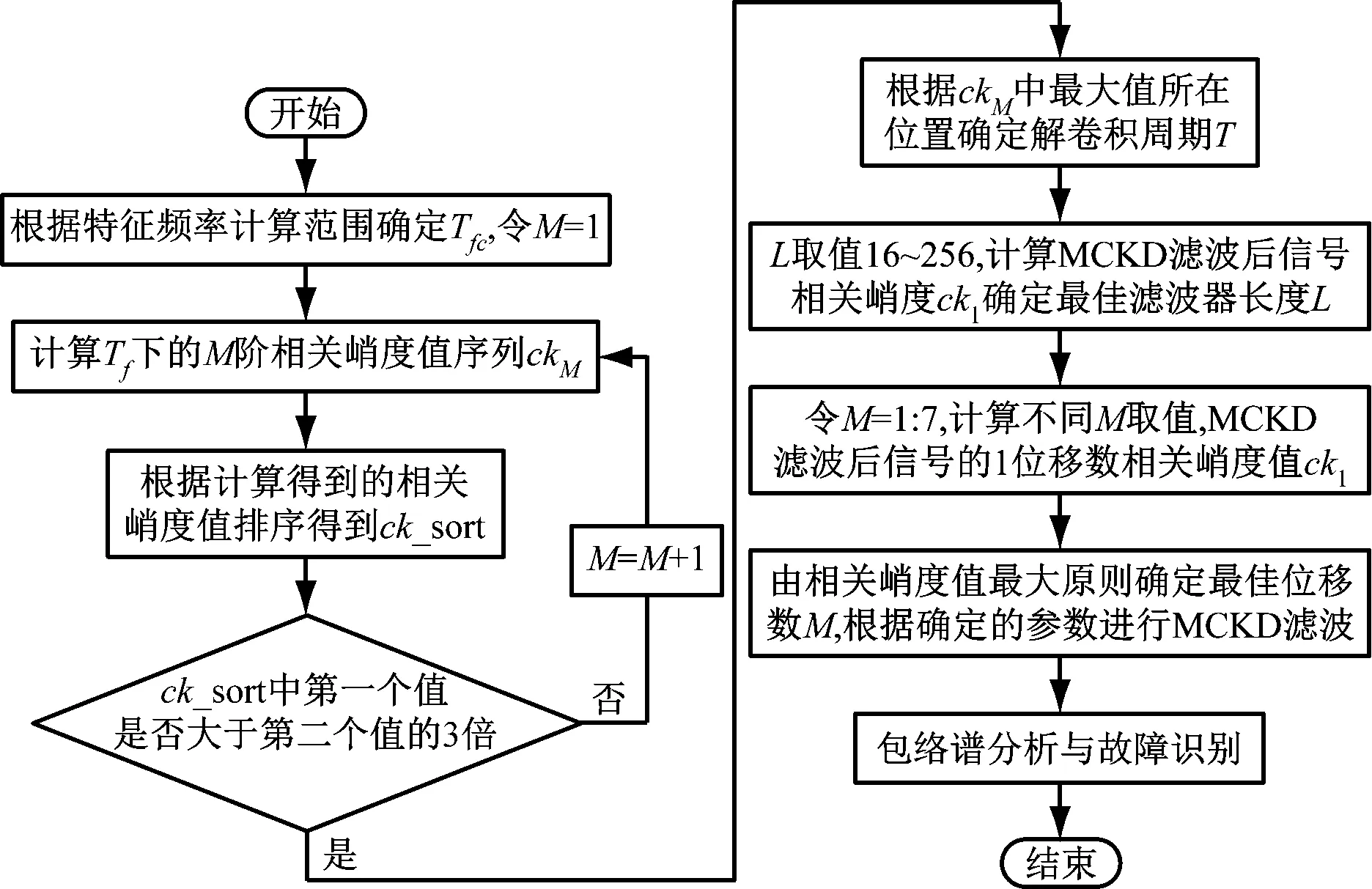
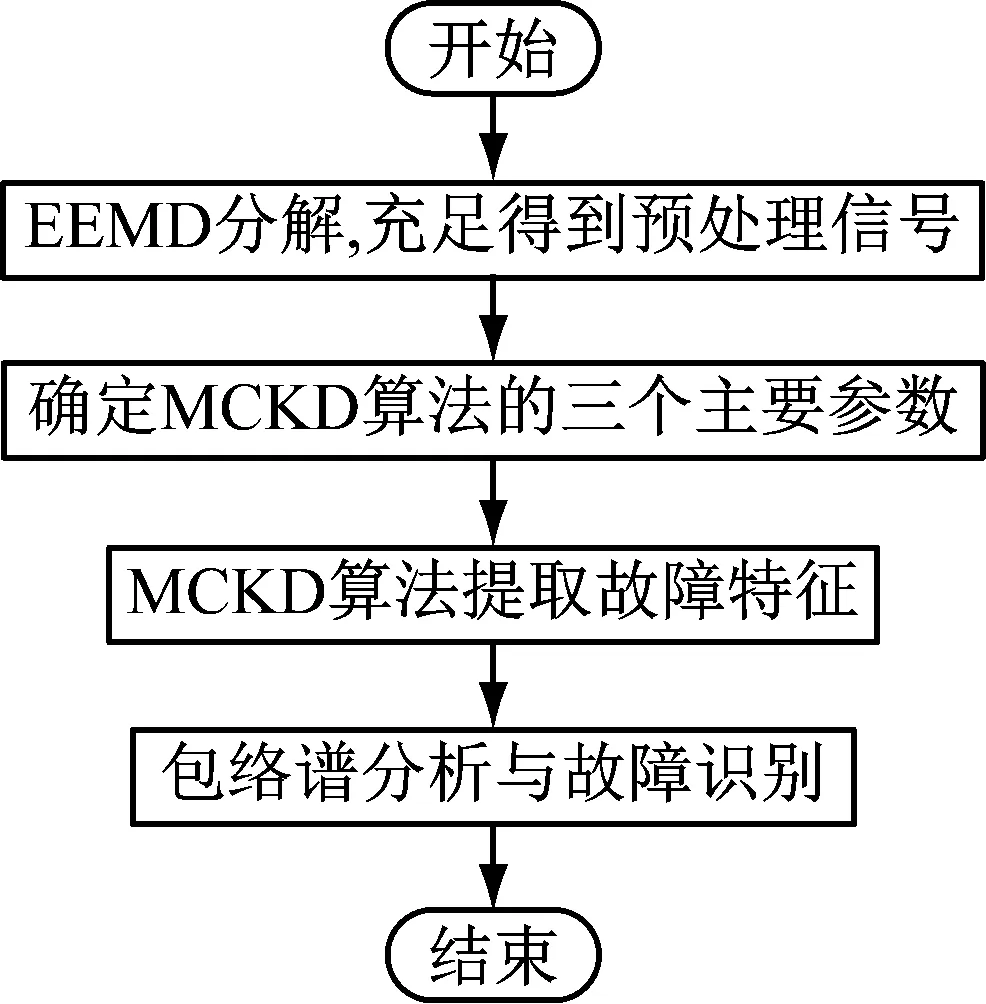
3 柔性薄壁轴承故障振动特征提取应用





3.1 EEMD处理原始信号
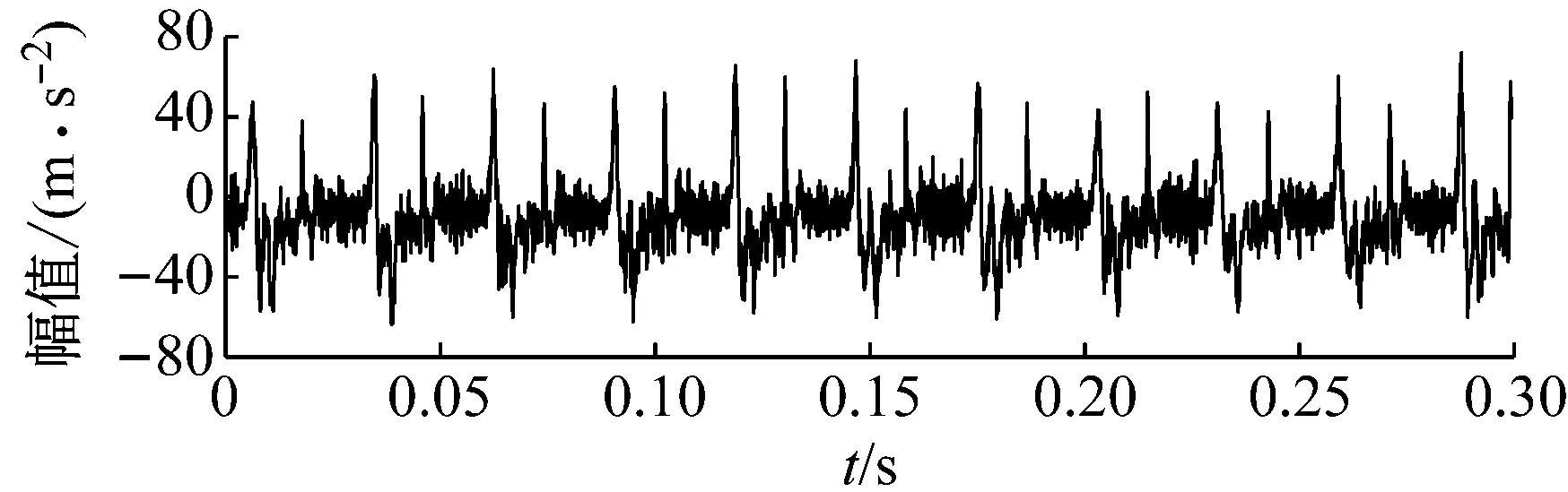
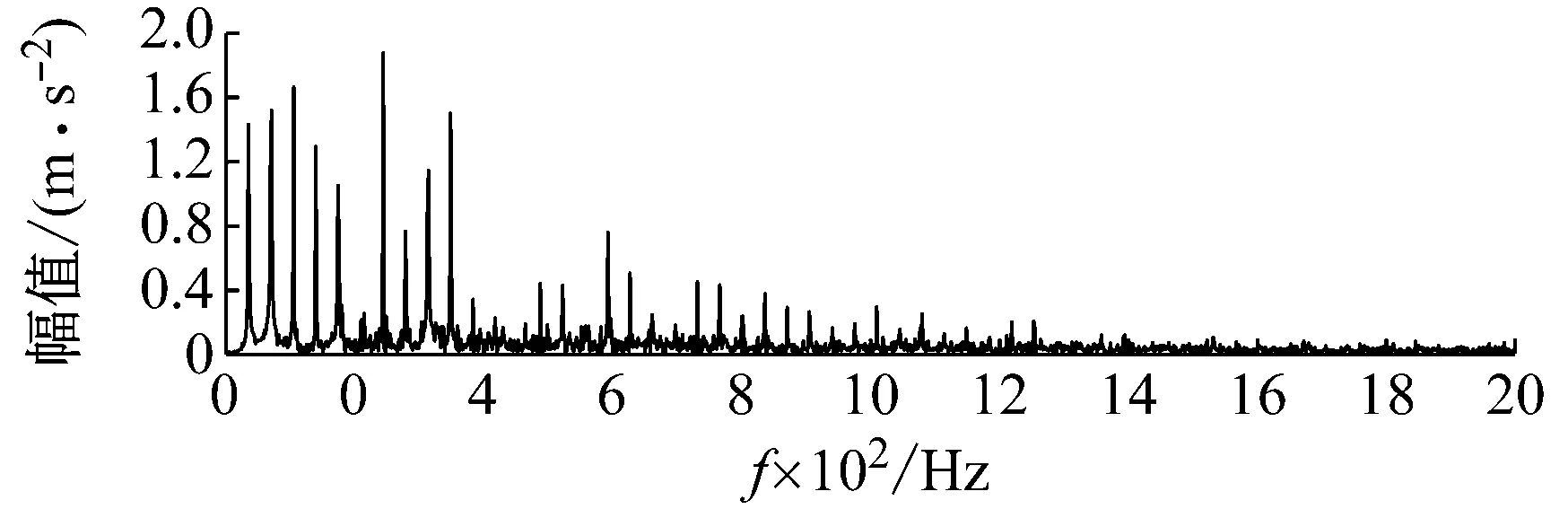

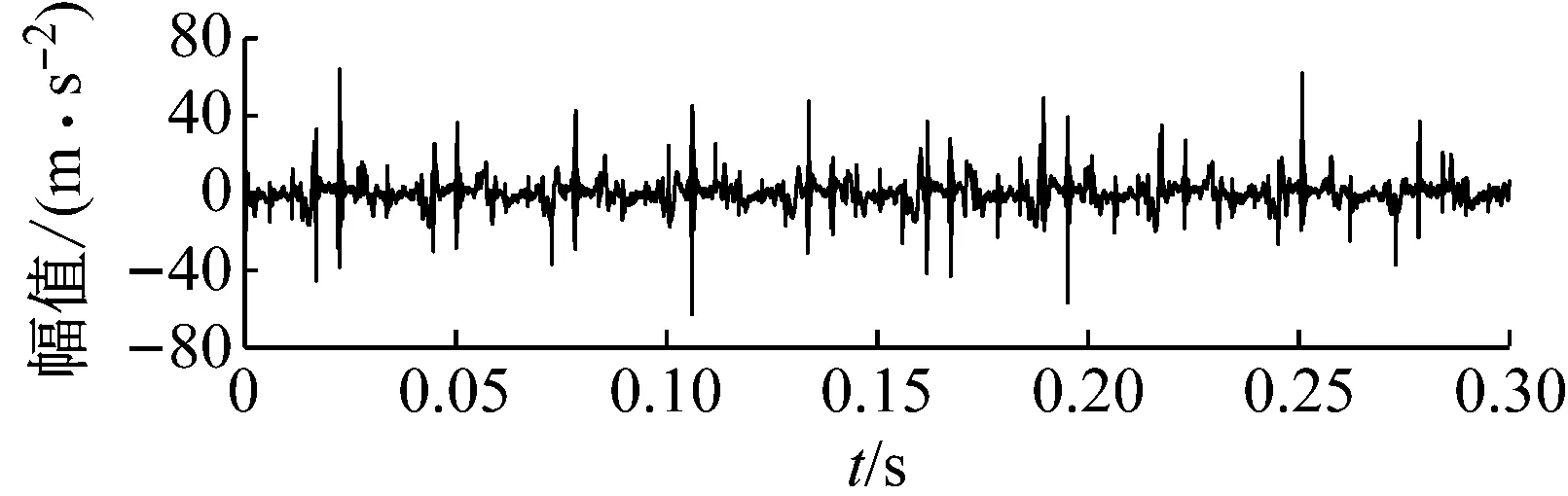
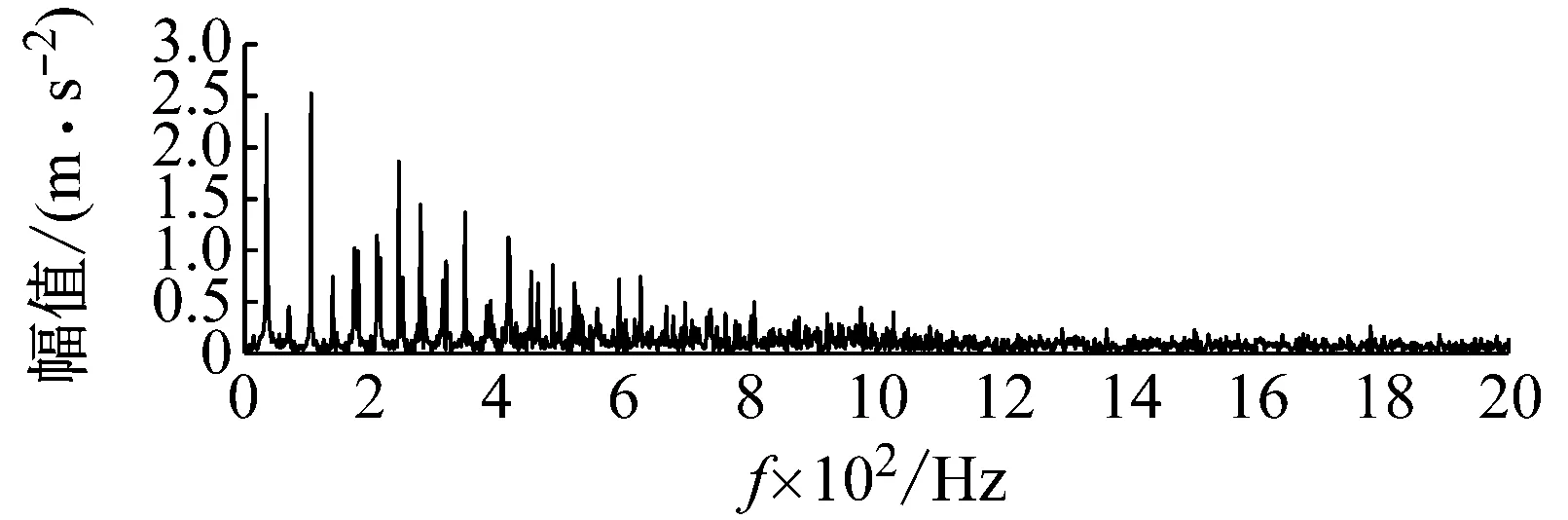
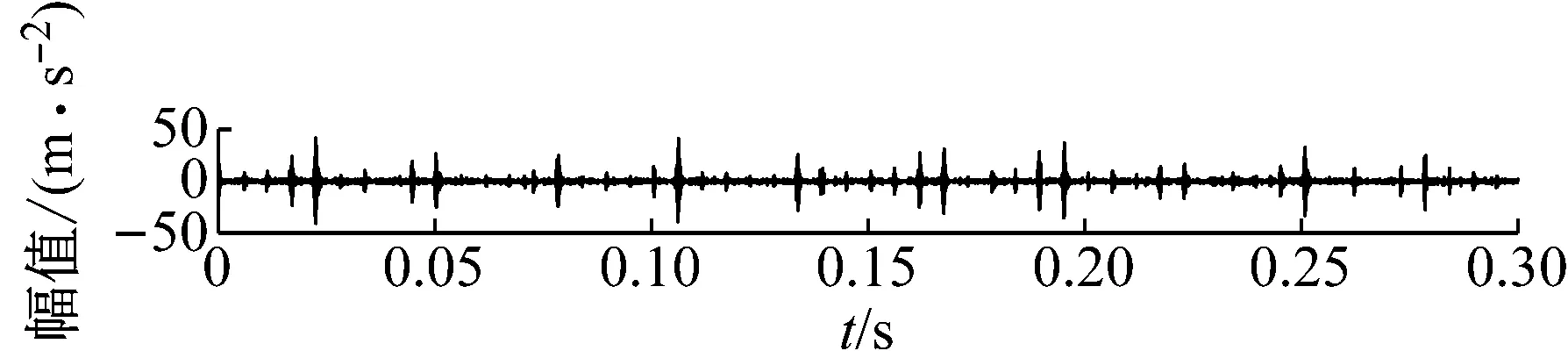
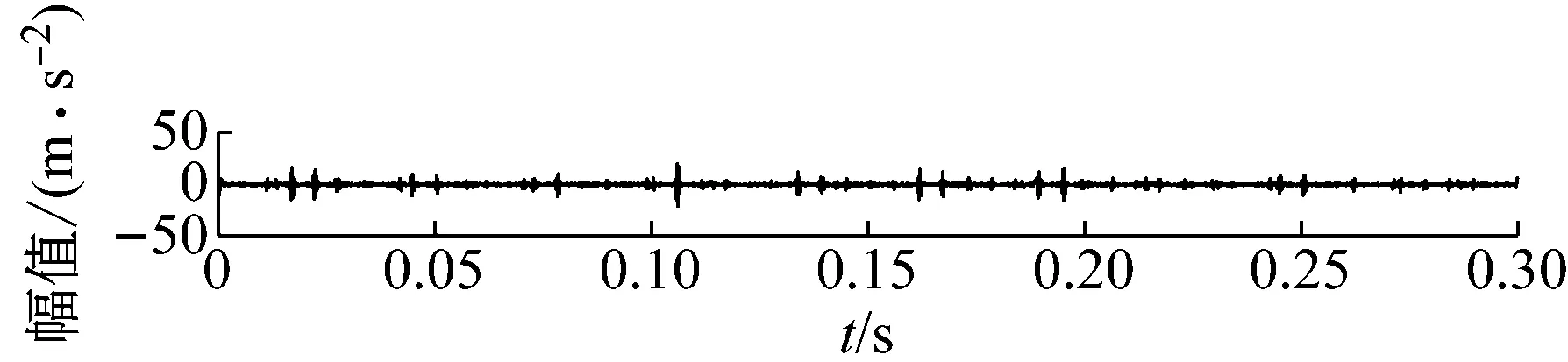
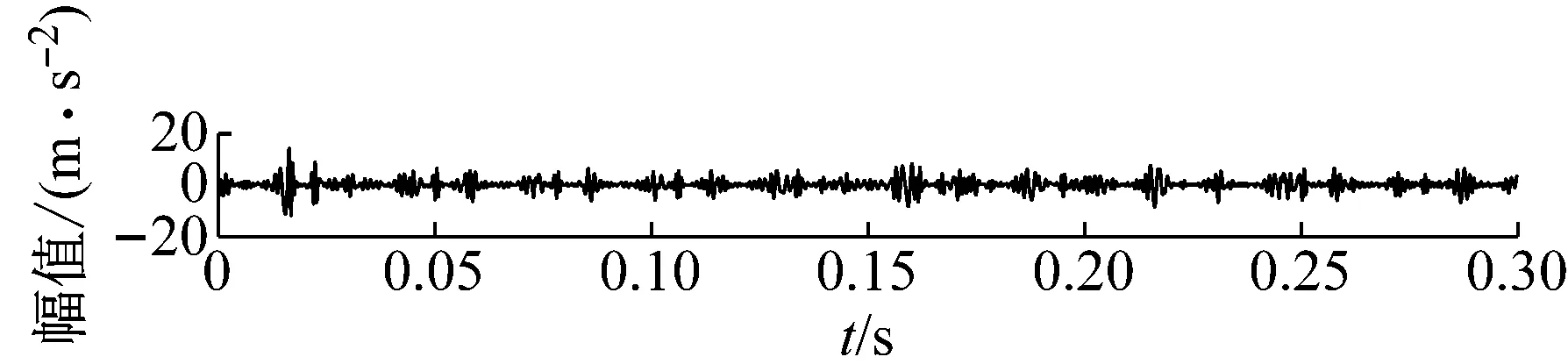
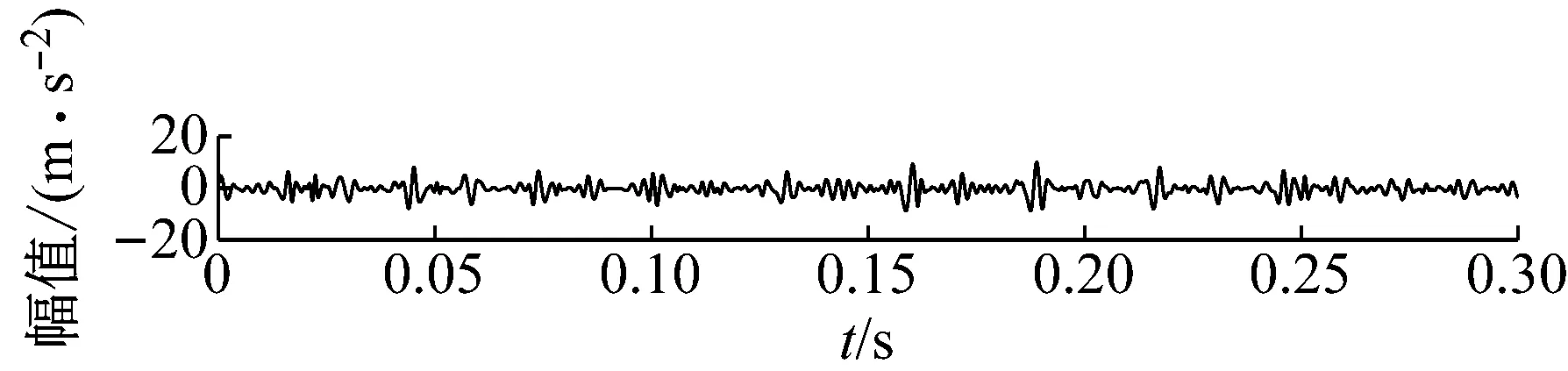
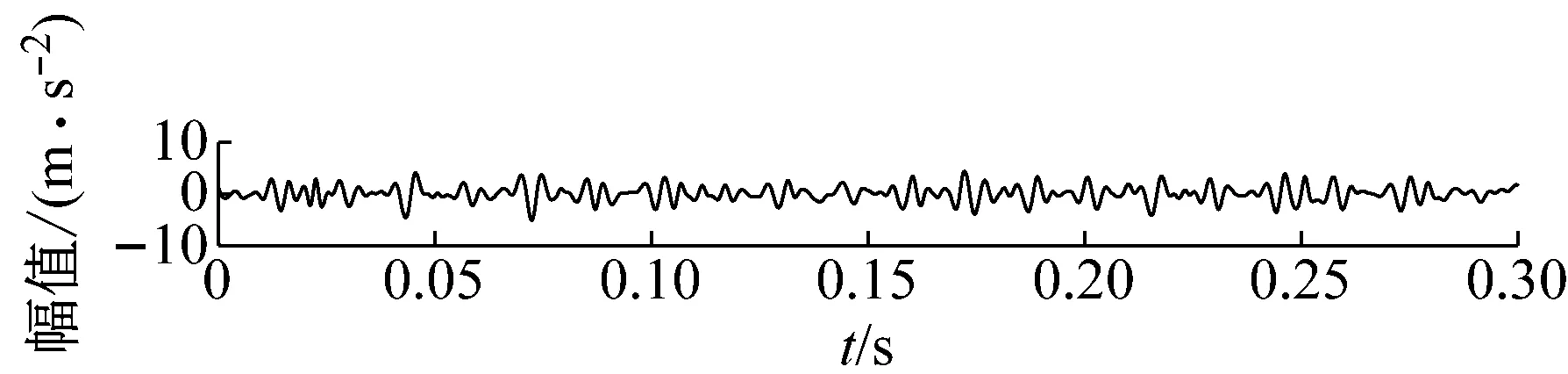
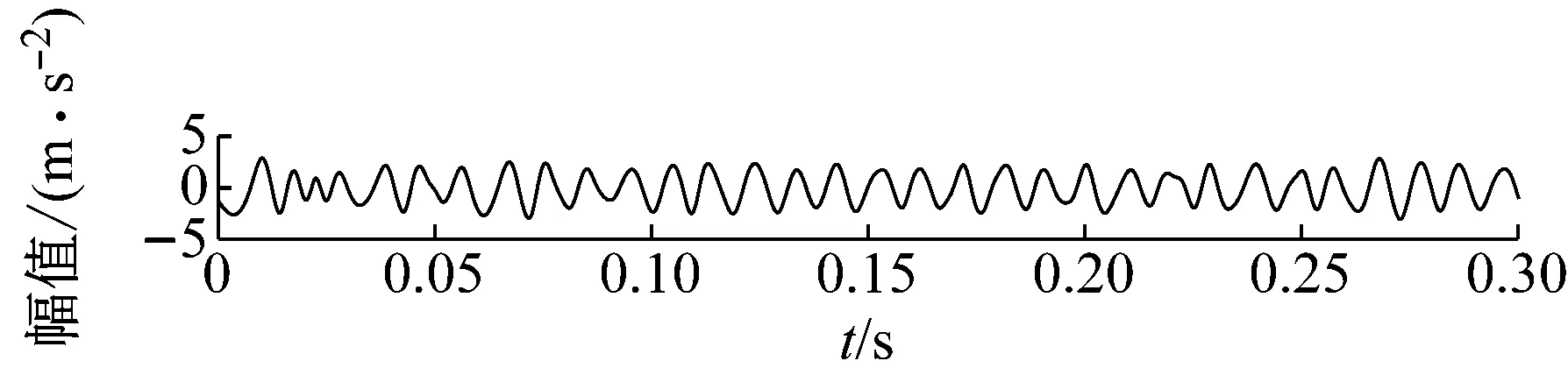
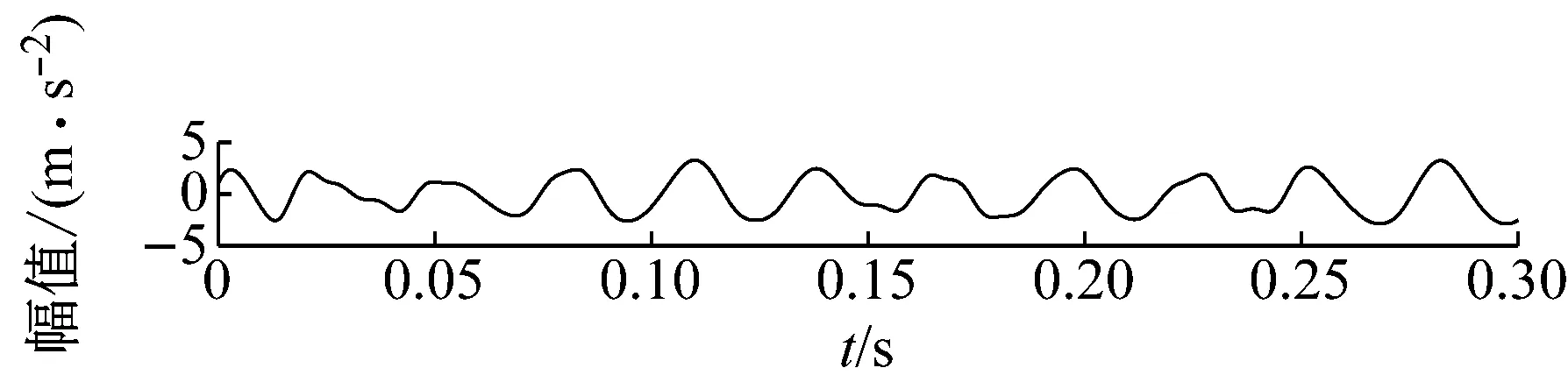
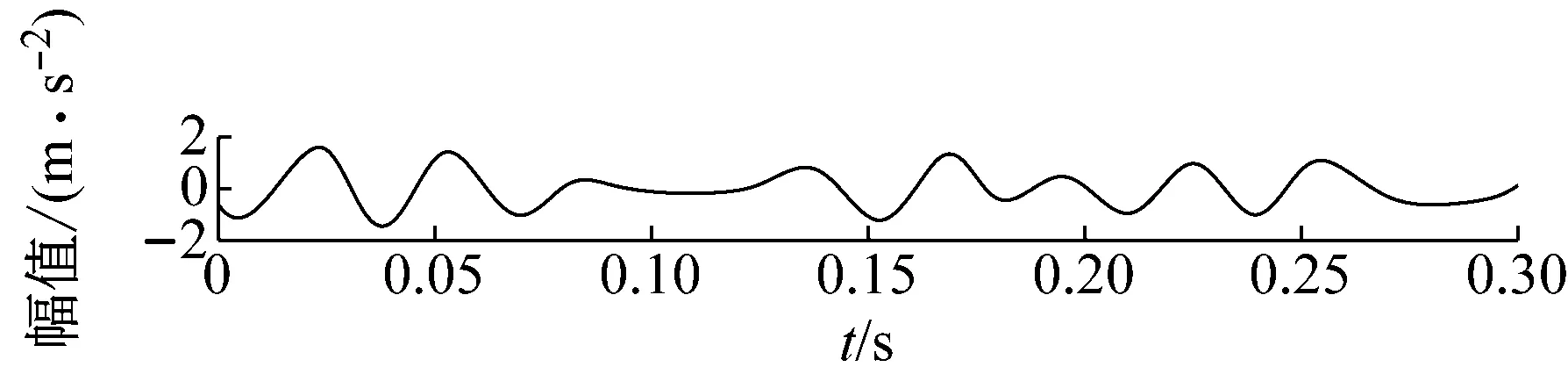
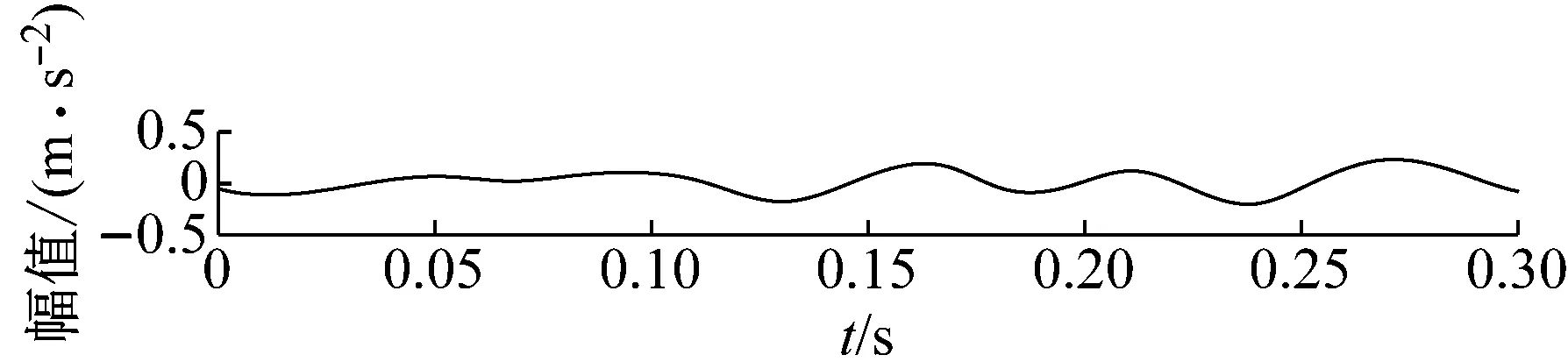
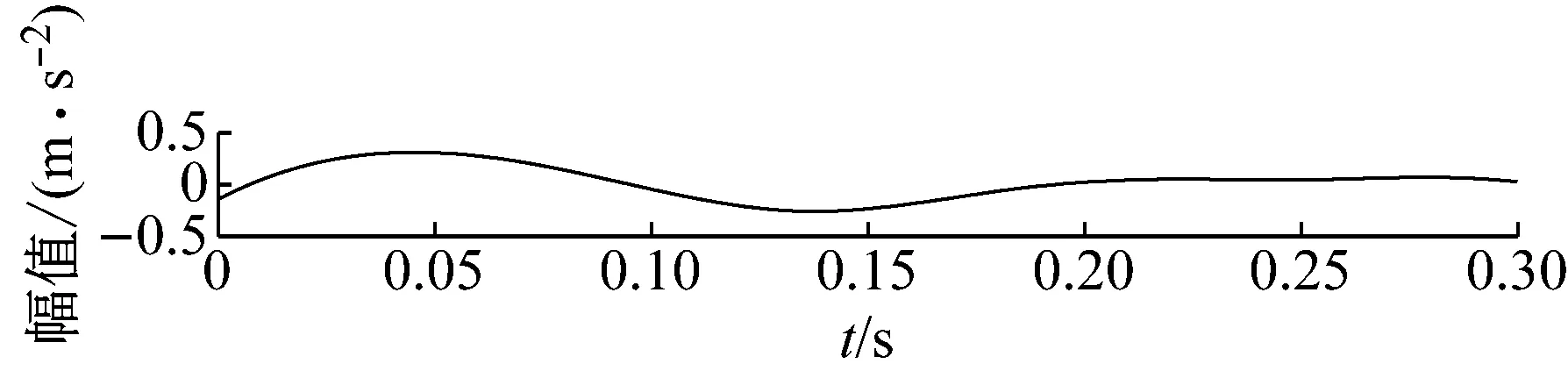
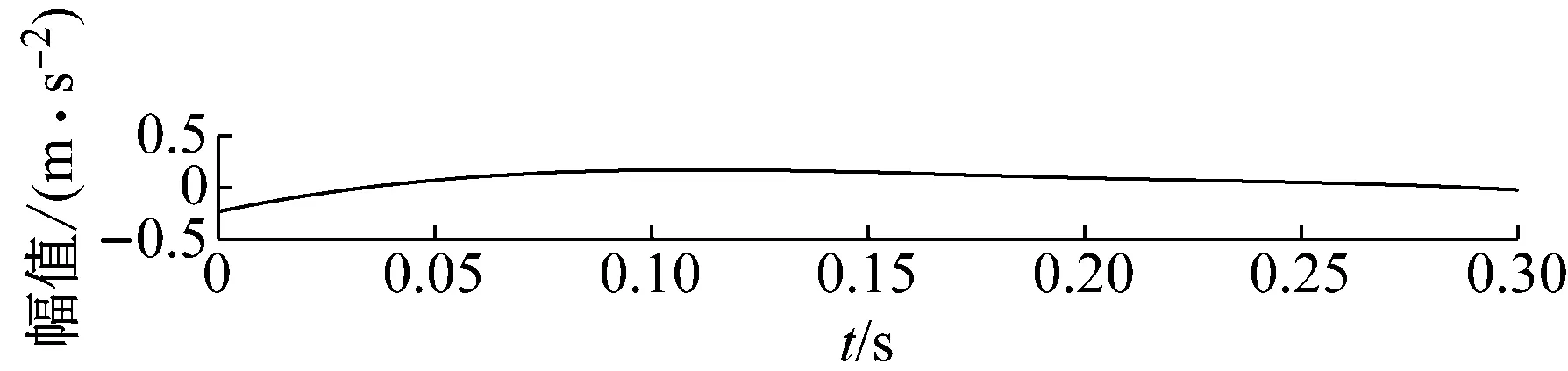
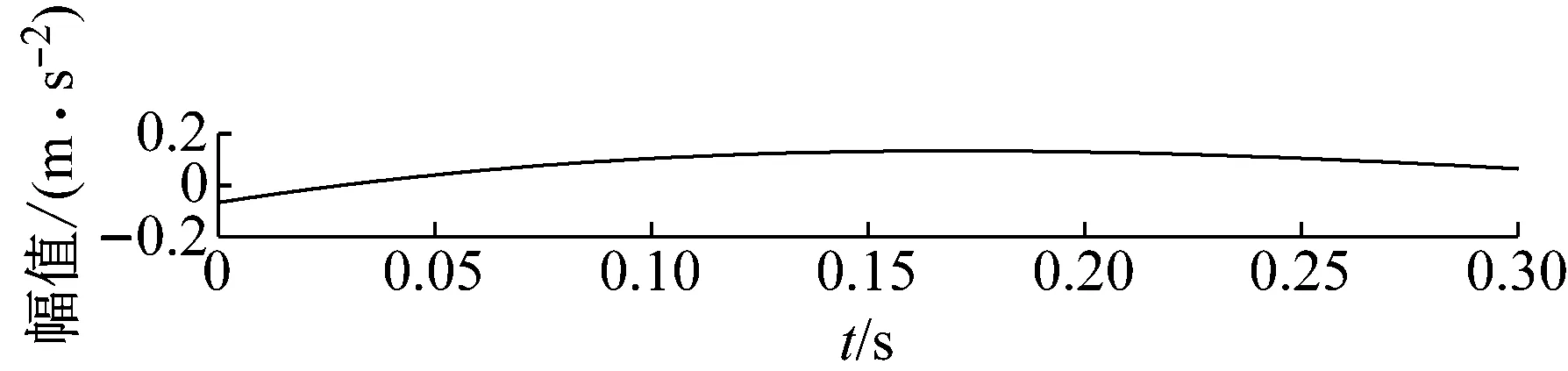
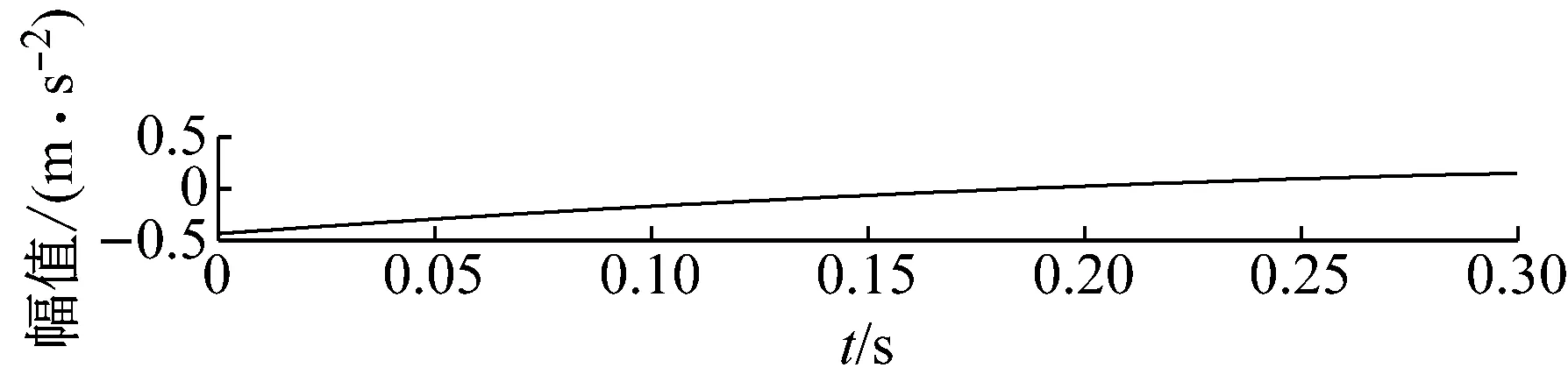
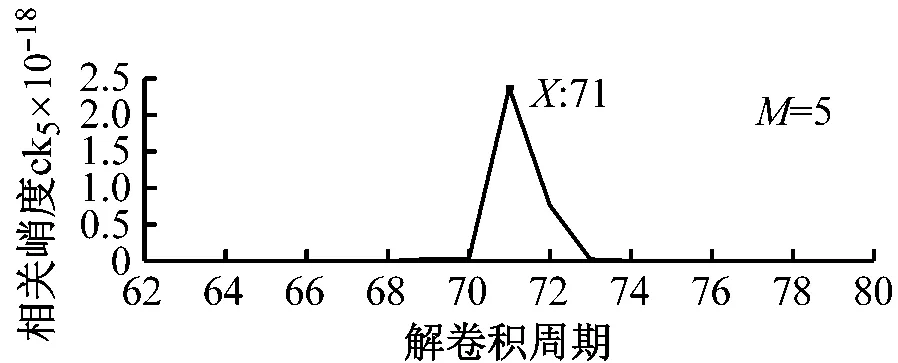
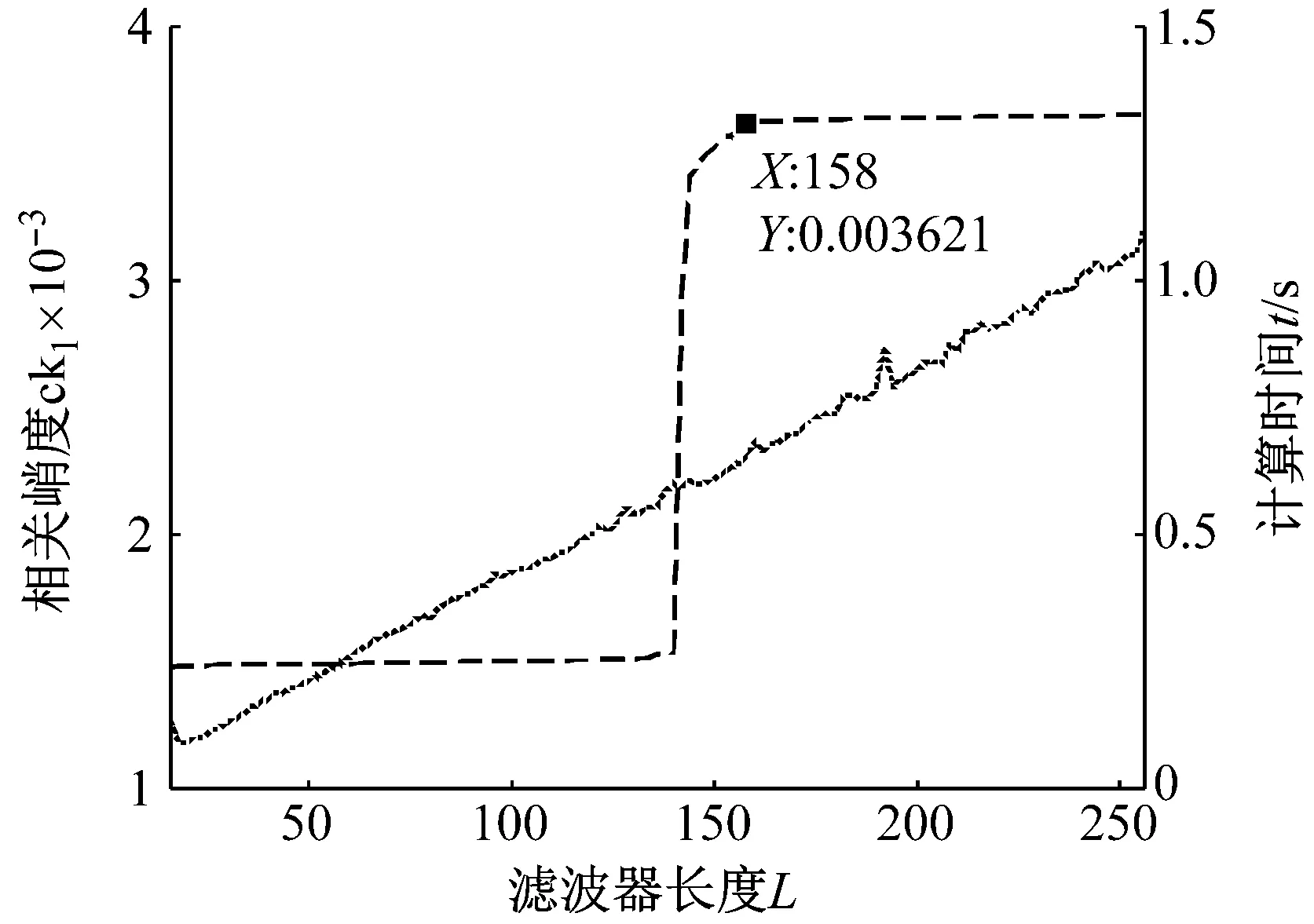
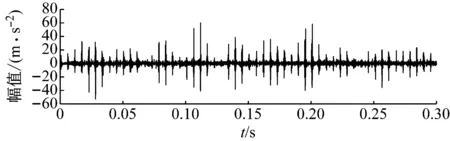
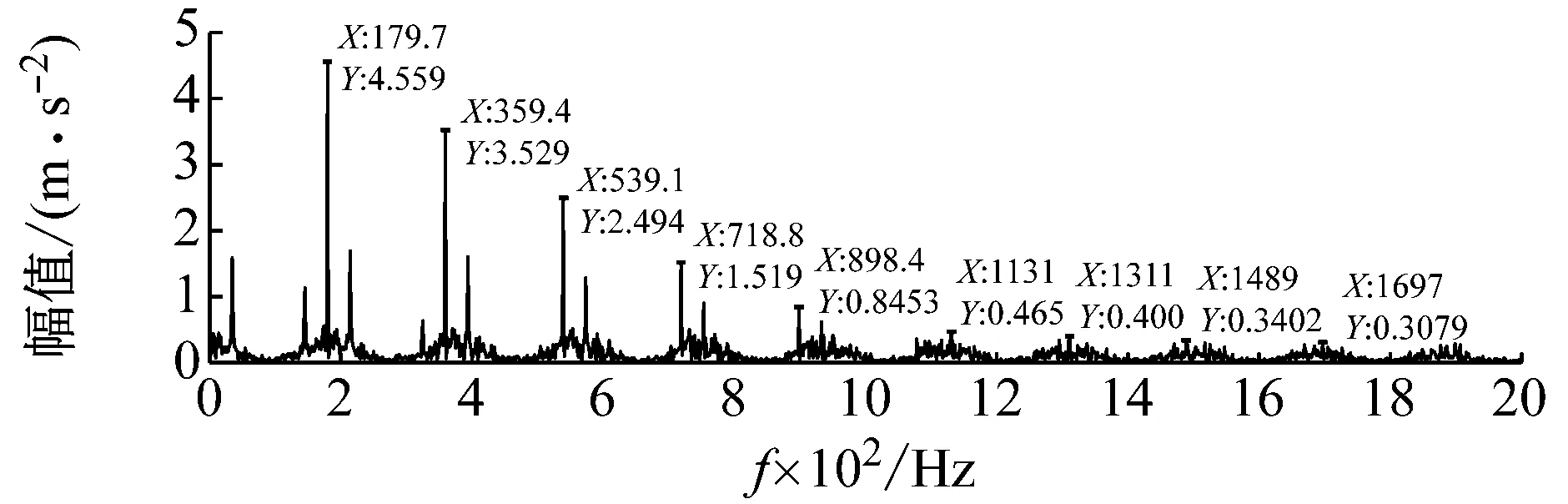
3.2 MCKD处理EEMD重构信号
4 结 论

