时滞反馈对三稳态van der Pol系统稳态概率密度的影响
段绪星, 吴志强, 李亚杰
(1.天津大学 力学系,天津 300350;2.天津市非线性动力学与混沌控制重点实验室,天津 300350)
噪声激励下非线性系统的动力学行为及其控制近些年来引起了国内外学者的广泛关注。噪声激励可以引发一系列动力学现象,如相干共振[1-2]、随机P分岔[3]、首次穿越[4-5]等。针对这些现象,人们引入了多种手段对其进行调控,如时滞差分反馈控制[6]、分数阶控制[7]等。因没有通用设计方法,人们常通过探讨控制参数的影响来为控制参数的选择提供参考。
广义van der Pol方程能呈现平衡点与极限环共存的多稳态现象,常作为多稳态系统的范例来探究随机激励的影响。Yamapi等[8]研究了高斯白噪声激励下的双稳态van der Pol系统,发现噪声强度可被看做系统的分岔参数。Mbakob等[9]研究了相关噪声诱导的随机P分岔现象,发现相关时间和噪声强度均能引起系统幅值概率密度曲线的定性变化。Zakharova等[10]的研究结果指出当双稳态van der Pol系统的稳定系数位于鞍结分岔点附近时,相干共振和随机P分相关。郝颖等[11]基于奇异性理论求出了噪声激励下三稳态van der Pol-Duffing系统幅值概率密度拓扑结构发生改变的临界参数条件。Zhang等[12]研究了循环噪声激励下的三稳态van der Pol系统,发现循环噪声的时滞和比例系数均会诱导系统发生随机P分岔。
近年来,诸多学者开始将时滞反馈控制应用到van der Pol系统中。Guo等[13]研究了位移和速度时滞反馈共同作用下的双稳态van der Pol系统,分析了时滞对系统双稳态区域的影响以及反馈强度和时滞引起的随机P分岔现象。Semenov 等[14]的研究结果表明时滞差分反馈可以控制van der Pol系统在Hopf分岔点附近的相干共振。Yang等[15]研究了多种噪声激励与时滞反馈共同作用下的双稳态van der Pol系统,发现其平均首次穿越时间与噪声强度以及系统振荡的主频有关。
当前关于三稳态van der Pol系统的理论研究,均是以分析不同类型噪声诱导的随机P分岔现象为主,对于引入时滞反馈控制的三稳态van der Pol系统的研究还未有涉及。本文主要研究时滞位移差分反馈对加性噪声激励下三稳态van der Pol系统稳态概率密度的影响。第1章应用随机平均法求解系统幅值的稳态概率密度函数;第2章分析确定性及随机情况下无时滞反馈调节系统的稳态响应,第3章从理论和数值两方面讨论存在时滞反馈时,反馈强度和时滞对系统稳态概率密度的影响,并给出了用于时滞反馈控制器参数设计的转迁集;第4章给出本文的结论。
1 理论模型及其幅值概率密度近似解
考虑加性高斯白噪声激励与时滞位移差分反馈共同作用下的广义van der Pol振子
K(x(t-τ)-x(t))+ξ(t)
(1)
为方便讨论时滞反馈的影响,下文如不特别说明,系统参数均取定值,其中ε=-0.172,α1=2.45,α2= 4.6,α3=2.5,α4=0.4,K为时滞反馈强度,τ为时滞(τ>0),ξ(t)是强度为D的高斯白噪声,且其均值和相关函数满足:〈ξ(t)〉=0,〈ξ(t)ξ(t+t1)〉=2Dδ(t1)。
系统(1)的解可设为如下形式:

(2)
其中A(t)、ψ(t)为关于时间t的随机过程。根据文献[16-17]可知,当时滞τ很小时,有
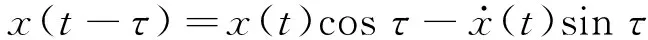
(3)
则系统(1)可表示为如下等效系统
(4)
其中
(5)
为求解系统(4)幅值的稳态概率密度函数,引入如下变换
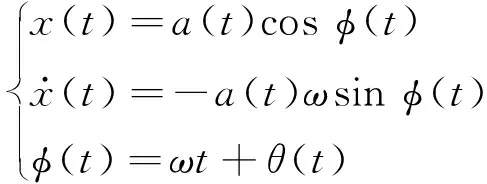
(6)
式中:a(t)为系统响应的幅值;ω为系统(4)的固有频率;θ(t)为初始相位。将式(6)代入式(4)中,得到标准方程如下
(7)
其中
f(acosφ,-asinφ)=(c+α1a2cos2φ-α2a4cos4φ+
α3a6cos6φ-α4a8cos8φ)aωsinφ
(8)
式(7)中高斯白噪声为平稳过程,(a,θ)近似为二维扩散过程,应用随机平均法,可得到稳态响应幅值a(t)和相位θ(t)的伊藤随机微分方程
(9)
其中
(10)
W1(t)和W2(t)是两个相互独立的单位维纳过程。幅值a不依赖于θ的变化,且a(t)是一个一维扩散过程,因此可得到其对应的FPK方程如下
(11)
(12)
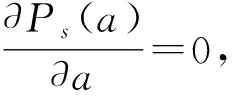
(13)
2 无时滞反馈系统的稳态响应
首先考虑无时滞反馈,即K=0的情况,此时系统(1)变为如下形式
(14)
当噪声激励强度D=0时,系统(14)退化为确定性系统,为了更好地说明该确定性系统的三稳态特性,图1给出了不同初始条件下确定性系统响应的相图。可见当初始条件不同时,系统存在三种吸引子,分别为大极限环、小极限环和零平衡点。
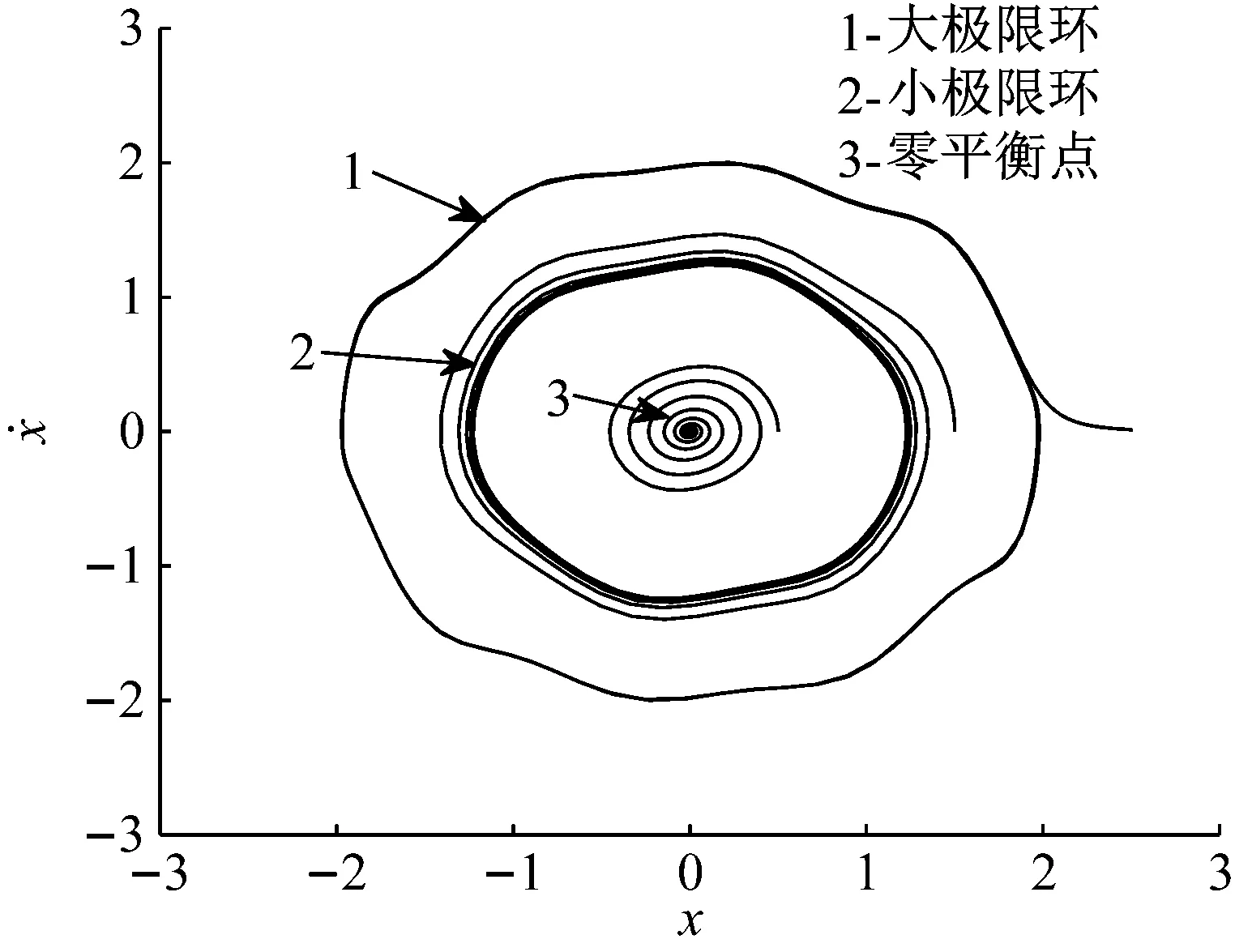
图1 不同初始条件下确定性系统响应的相图
由于确定性系统的三稳态特性,当存在噪声激励,即噪声强度D≠0时,此时系统的响应会在零平衡点附近的振荡、小幅值振荡和大幅值振荡这三种振荡模式间切换,如图2所示。同时图3给出了系统幅值的稳态概率密度曲线,其中实线为理论结果,星号为Monte Carlo数值模拟的结果。可见当D=0.01时,稳态概率密度函数曲线存在三个峰,且此时系统小幅值振荡的概率较大。对于时滞位移差分如何影响随机系统的响应将在下节讨论。

(a) 位移的时间历程
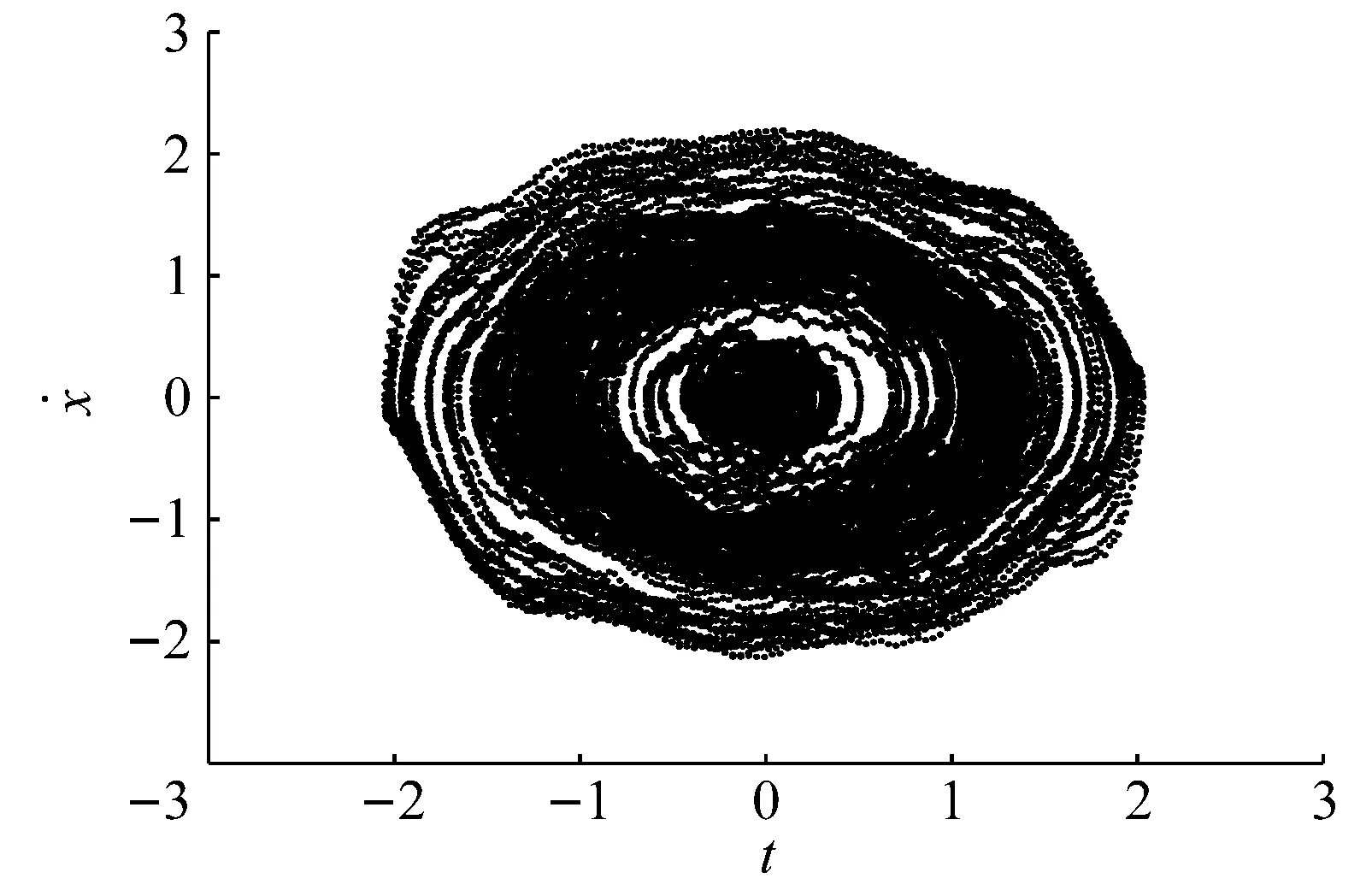
(b) 响应的相图

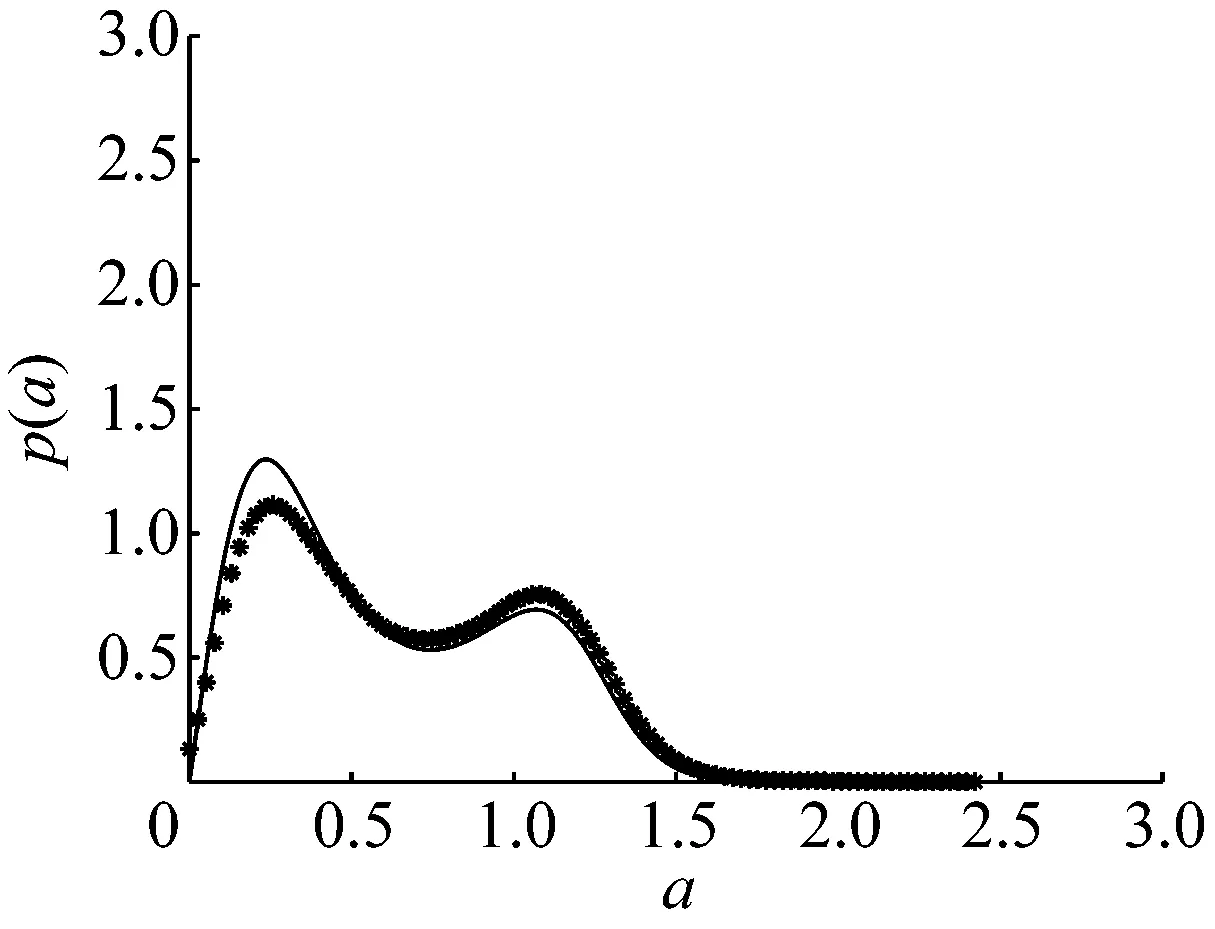
图3 D=0.01时系统稳态概率密度曲线
3 时滞反馈对系统稳态概率密度的影响
3.1 时滞对稳态概率密度的影响
取定反馈强度K=0.5,探讨时滞τ对系统稳态概率密度的影响。根据式(13)可得噪声强度D=0.01时稳态概率密度函数极值点am随时滞τ的演化图,如图4所示,其中实线代表函数的极大值点、虚线代表函数的极小值点。对每一组参数下的原系统(1)进行Monte Carlo模拟,并提取概率密度分布的极大值点和极小值点便可验证理论结果的正确性,数值结果也在图4中给出,其中星号为数值方法得到的概率密度分布的极大值点,圆圈为数值方法得到的概率密度分布的极小值点。可见当时滞τ分别在区间[0,0.045)、[0.045,0.107)、[0.107,0.3]时,概率密度函数极值点的分布有本质区别。

图4 D=0.01时极值点am随时滞τ的演化

(a) τ=0.02
(b) τ=0.08

(c) τ=0.14
从图5可知,当时滞τ=0.02时,稳态概率密度曲线存在三个峰,此时系统的稳态响应在零平衡点附近的振荡、小幅值振荡和大幅值振荡这三种振荡模式间切换,但小幅值振荡的概率较大,且在零平衡点附近振荡的概率稍大于大幅值振荡的概率,这与图3中无时滞反馈的情况略有区别;当时滞τ=0.08时,稳态概率密度曲线存在两个峰,此时系统的稳态响应在零平衡点附近的振荡、小幅值振荡这两种振荡模式间切换,系统的大幅值振荡消失,且此时在零平衡点附近振荡的概率较大;当时滞τ=0.14时,稳态概率密度曲线仅存在一个峰,此时系统在零平衡点附近的振荡较为显著。
因此,从上述分析结果来看,噪声强度D=0.01,反馈强度K=0.5时,稳态概率密度曲线的拓扑结构在时滞τ增加的过程中经历了两次转变:三峰(平衡点处、小极限环处、大极限环处)→双峰(小极限环、大极限环处)→单峰(平衡点处)。并且,随着时滞τ的增加,系统的大幅值振荡和小幅值振荡受到了抑制。从随机分岔的角度来看,时滞τ的改变诱导系统发生了两次随机P分岔,这也意味着该随机系统的分岔行为可以通过时滞来调节。
3.2 反馈强度K对稳态概率密度的影响
取定时滞τ=0.1,探讨反馈强度K对稳态概率密度的影响,根据式(13)可得噪声强度D=0.01时稳态概率密度函数的极值点am随反馈强度K的演化图,如图6所示,其中实线代表函数的极大值点、虚线代表函数的极小值点,星号为数值方法得到的概率密度分布的极大值点,圆圈为数值方法得到的概率密度分布的极小值点。可见当反馈强度K分别在区间[-1,-0.364)、[-0.364,-0.257)、[-0.257,0.226) 、[0.226,0.537)、[0.537,1]时,概率密度函数极值点的分布也有本质的区别。
图7给出了不同反馈强度K下系统幅值的稳态概率密度曲线,其中实线为理论结果,星号为对原系统(1)进行Monte Carlo数值模拟的结果,两者吻合较好。
从图7可知,当反馈强度K=-0.4时,稳态概率密度曲线存在一个峰,此时系统大幅值振荡较为显著;当反馈强度K=-0.3时,稳态概率密度曲线存在两个峰,此时系统的稳态响应在小幅值振荡与大幅值振荡这两种振荡模式间切换,但大幅值振荡的概率较大;当反馈强度K=0.04时,稳态概率密度曲线存在三个峰,此时系统的稳态响应在零平衡点附近的振荡、小幅值振荡和大幅值振荡这三种振荡模式中切换,但小幅值振荡的概率较大;当反馈强度K=0.3时,稳态概率密度曲线存在两个峰,此时系统在零平衡点附近的振荡和小幅值振荡这两种振荡模式间切换,并且在零平衡点附近振荡的概率和小幅值振荡的概率相近;当反馈强度K=1时,稳态概率密度曲线仅存在一个峰,此时系统在零平衡点附近的振荡较为显著,而小幅值振荡和大幅值振荡消失。
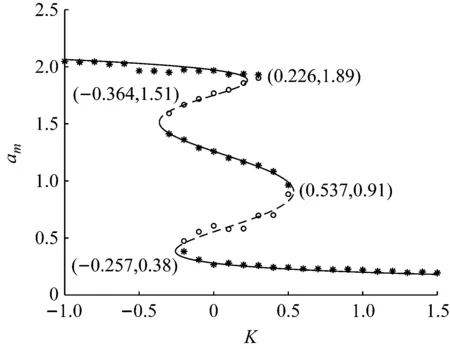
图6 D=0.01时极值点am随反馈强度K的演化
因此,从上述结果来看,当噪声强度D=0.01,时滞τ=0.1时,稳态概率密度曲线的拓扑结构在反馈强度K增加的过程中经历了四次转变:单峰(大极限环处)→双峰(小极限环处、大极限环处)→三峰(平衡点处、小极限环处、大极限环处)→双峰(平衡点处、小极限环处)→单峰(平衡点处),这与3.1节中时滞(对系统稳态响应的影响机制有本质不同。同时,也不难发现,在反馈强度K不断增加的过程中,大幅值振荡受到了抑制,而在平衡点附近的振荡得到了增强,这表明通过改变时滞反馈控制参数,可以使系统处于不同的振荡模式中。此外,从随机分岔的角度来看,反馈强度K的增加诱导系统发生了四次随机P分岔,这意味着该随机系统的分岔行为也可以通过反馈强度K来调节。
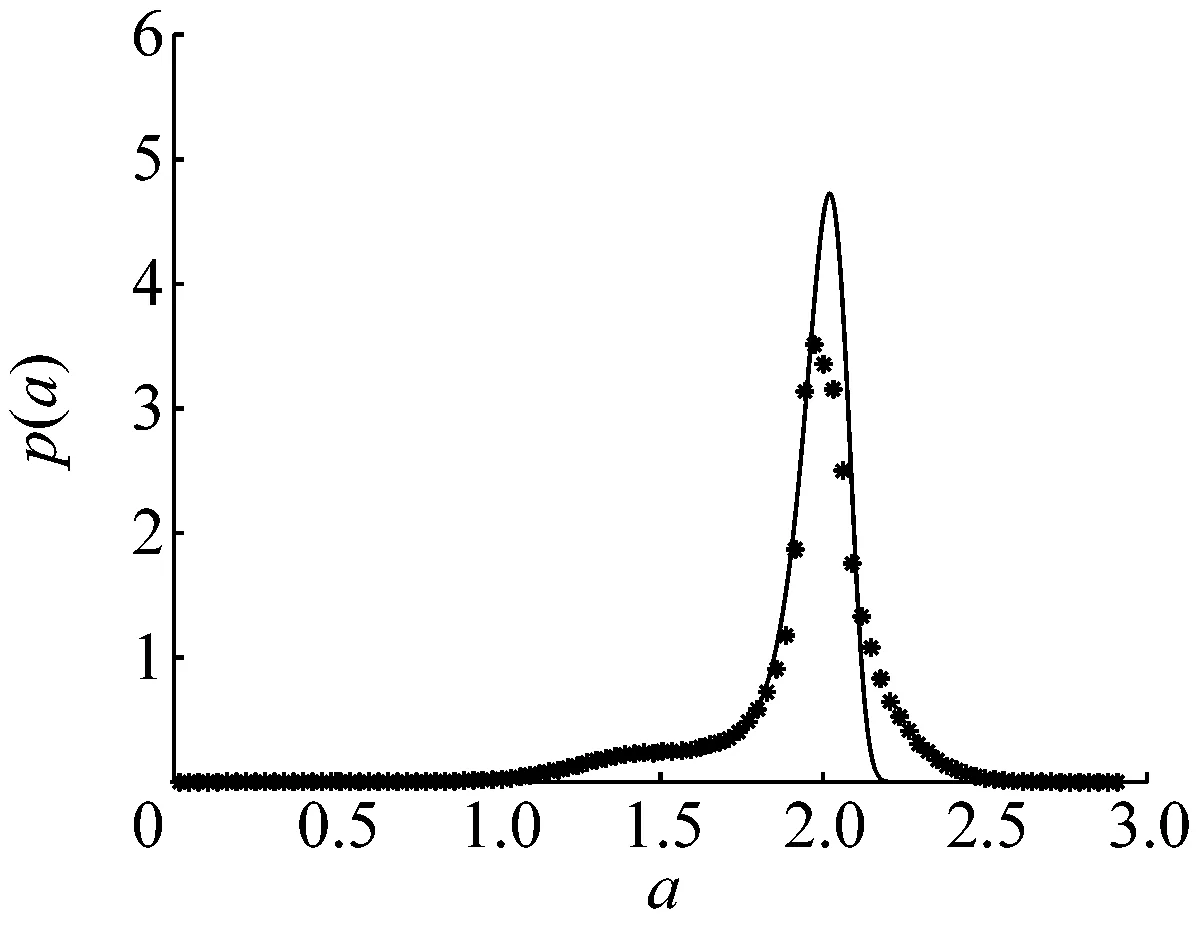
(a) K=-0.4
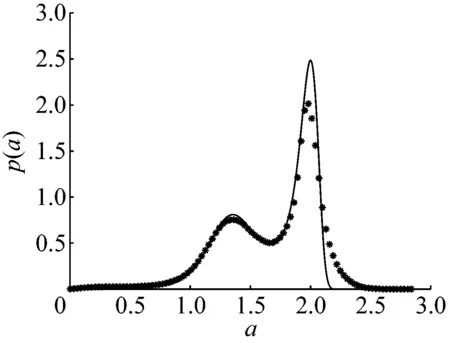
(b) K=-0.3
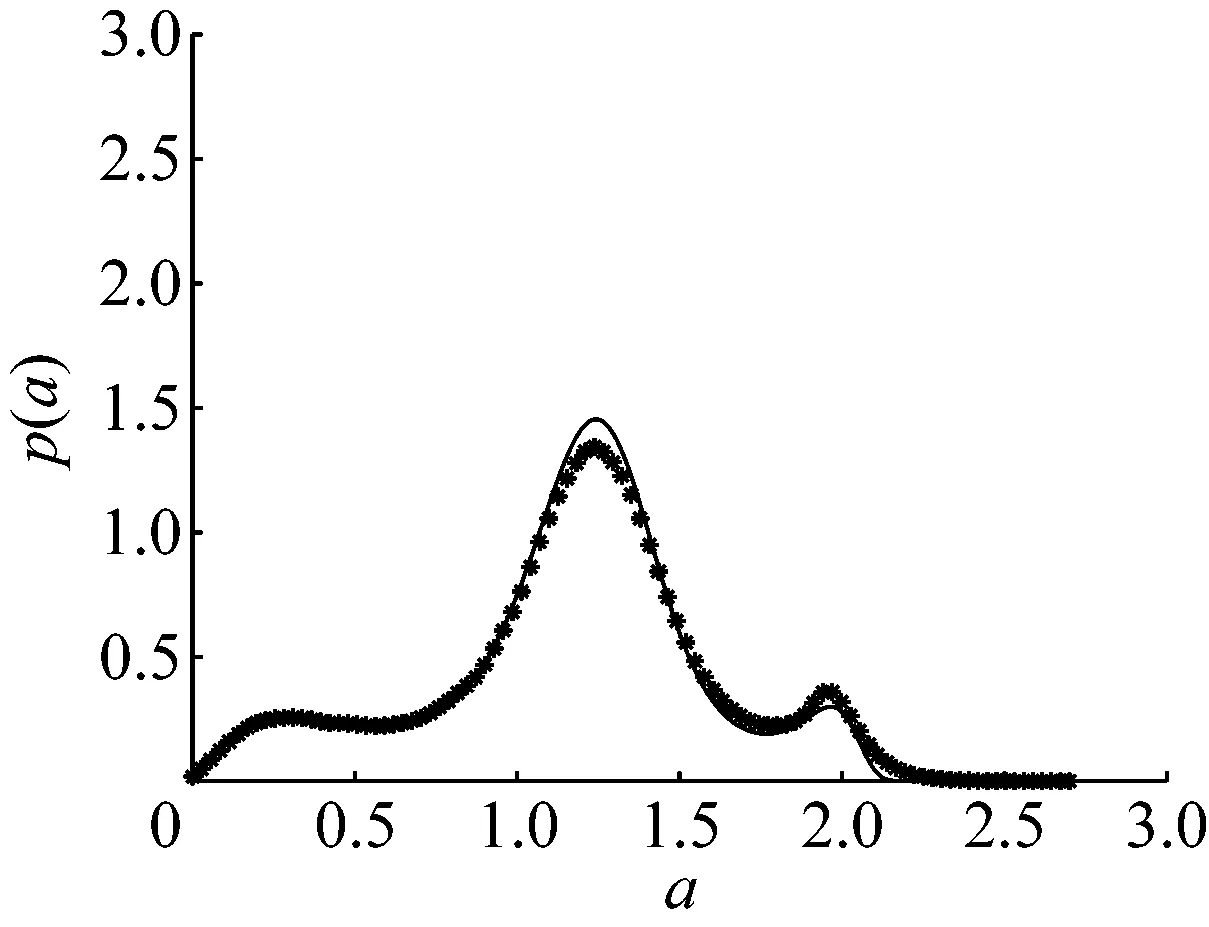
(c) K=0.04

(d) K=0.3

(e) K=1
3.3 时滞反馈控制参数设计
3.1节和3.2节分别探讨了时滞和反馈强度对系统稳态概率密度的影响,相关结论可用于时滞反馈控制器的单参数设计,但仍未解决时滞τ和反馈强度K的双参数设计问题,为此,需计算出导致幅值概率密度函数极值点数目发生变化的临界参数集合,即(τ,K)参数平面内的转迁集。
仍考虑噪声强度D=0.01的情况,通过求解式(13)的正解个数在(τ,K)参数平面的分布就可以得到转迁集,如图8所示,参数平面被分成了三个区域,不同区域内的正根个数不同。当参数(τ,K)在区域1时,仅有一个极值点,函数曲线仅有一个峰。当参数(τ,K)在区域2时,幅值概率密度函数存在三个极值点,函数曲线有两个峰。当参数(τ,K)在区域3时,幅值概率密度函数存在五个极值点,此时函数曲线有三个峰。从图中还可以发现,当时滞(增大时,三峰及双峰参数区域所对应的反馈强度K的范围逐渐变小,而单峰参数区域所对应的反馈强度K的范围逐渐变大。
从参数设计的角度看,选择(τ,K)的不同组合,可使受控系统幅值的稳态概率密度曲线具有不同的拓扑结构,从而对随机系统的稳态响应进行调控。此外,由于噪声强度会对稳态概率密度产生影响,在选择控制参数时,需要对不同噪声强度的情况进行具体分析。因此,针对本文所给参数,图8实际上解决了面向幅值概率密度调节的时滞反馈控制参数设计问题,更一般情况下的时滞反馈控制参数设计还有待进一步讨论。

图8 D=0.01时(τ,K)平面内的转迁集
4 结 论
基于随机平均法探讨了时滞位移差分反馈对加性噪声激励下三稳态van der Pol系统稳态概率密度的影响,得到如下结论:
在小噪声激励的情况下反馈强度和时滞的变化均可以影响系统的稳态响应,但是两者的影响机制有所不同。时滞的增大可以使稳态概率密度曲线从三峰过渡到单峰;而反馈强度的增大则会使系统稳态概率密度曲线的拓扑结构经历四次转变。
通过求解幅值概率密度函数极值点分布得到了时滞与反馈强度平面内的转迁集,可直接用于时滞反馈控制的参数设计,更一般情况下的参数设计有待进一步分析。

