非线性尾流相互作用研究

王程英, 张建生

非线性尾流相互作用研究

王程英, 张建生

(西安工业大学 理学院, 陕西 西安, 710021)

在限制水域中, 快速船舶的尾迹最重要的特征是在船舶前方能产生孤立波。文中基于Korteweg-de Vries型方程和Hirota双线性形式的符号和辅助结果, 得到不同相位变化中的双孤子解。利用Mathematica软件仿真得到了KP(Kadovtsev-Petviashvili)方程双孤子解在不同相位变化中的所有可能波型以及双孤子解分解结构与线性叠加的波形, 为理解KP方程双孤子解、双孤子相互作用及其形态结构特征奠定了基础。基于无量纲KP方程的双孤子解, 仿真得到标准坐标下等振幅和非等振幅入射孤子相互作用区域的表面高度。结果表明, 等振幅入射孤子的振幅与参考孤子的振幅相差0.01%比相差1%的相互作用波峰空间范围大; 非等振幅的2个入射孤子的相互作用主要导致了2种入射孤子波峰的弯曲。利用Matlab软件仿真得到入射孤子和相互作用中心双孤子解的不同波峰, 通过调节参数对比相互作用孤子的坡度, 结果表明沿波峰的传播方向,值越大, 相互作用孤子的轮廓越窄, 坡度越大。

船舶尾流; 双孤子解; 孤子相互作用; 表面高度; 坡度

0 引言

由于尾流对声波和光波具有吸收、散射等作用[1], 因此在海战中可能会干扰声学设备和光学仪器的有效使用和操作。尾流的存在可能提供一种探测、跟踪或识别产生尾流的舰船和潜艇的方法[2]。为了对不同类型的尾流进行探测、跟踪或识别, 很多研究者对尾流所具有的声学特性、光学特性、电磁学特性及热特性等物理学特性做了大量研究[3-6]。由于尾流会沿着航行方向延伸到舰船长度的很多倍, 即使在船桥和桅杆顶端, 对尾流的轮廓很难有一个整体视野[7]。

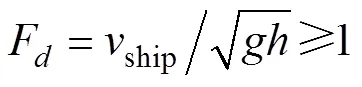
以跨临界速度航行的船舶所激发的孤子前体有时被认为是造成海岸线上一些危险的海啸波的原因, 孤子前体通常有小的振幅[11-12]。构成危险更可能的原因是, 当主要的发散波传播到浅水区时, 它们会变成高度椭圆余弦波或具有孤立波性质。快速渡轮波浪的显著特点是波峰较长, 因此能够长时间地与类似的波浪相互作用, 因为孤子船波的高度可以达到1~1.5 m[13], 其高度和坡度的非线性放大可能导致严重的危险。船舶在平行航向上运动时, 可能发生类孤子船波的相互作用, 但相关的实验都集中在评估可能的波阻降低[14],只有当入射波的高度和它们的交角特别平衡, 并且与孤子船波覆盖的区域相比, 在每个时刻被高驼峰占据的海面比例明显较小时, 才可能出现大表面高度和有陡峰的大面积区域。然而在某一点上出现近共振相互作用孤子的概率是相当大的, 因为它们可能是长寿命的结构, 在有利的条件下可以跨越大的海域[15]。畸形波的存在和外貌在许多情况下都可以用基本的线性模型来解释, 如波与长波、洋流或水深的相互作用或不同长度的线性波的叠加。畸形波激发的非线性机制(例如波列在纵向和横向扰动下的调制不稳定性[16]或非线性波在类似波涛汹涌的情况下聚焦[17-18])通常更为合适。所列机制通常在特定点上产生一个短时间的大瞬态波群。长峰孤波的非线性叠加可能是在有利条件下具有无限寿命的空间局部化极端地表高程的一个挑战性来源。风暴波(通常为短波峰和极不规则波)是不常见的, 但当来自不同方向的2个或多个涌浪系统在某些海域(如小岛或海山的背风侧)相遇时, 可能会发生风暴波[19]。在未来海洋安全领域, 尾流与异常浪研究将是必不可少的研究方向, 为海洋安全现代化、科学化管理提供了发展的条件, 对海洋环境可持续发展具有深远意义[20]。

1 船舶尾流非线性分量

船舶尾流的非线性分量示意图如图1所示。船舶尾流通常是典型的开尔文波系统与几种不同类型的非线性系统的组合。船舶尾流的非线性分量包括以下几部分。

1) 窄V型尾流[21]: 一艘船通常会在航线上留下一片剧烈的湍流。它是舰船尾迹中最具非线性的部分, 能够持续多个小时, 通常能在太空中被探测到。它是一条由短波阻尼引起的暗线, 同时伴随大气中的尾迹(称为船迹, 主要由船的排气羽流引起), 尾迹会延伸数百千米的距离, 高度约750 m, 持续约10 h。卫星图像有时显示2种非常窄的V型尾流成分, 沿某些射线的半角范围在1º和开尔文尾流的极限半角之间。这种信号只能在微风(风速小于3 m/s)中检测到, 它们出现在湍流尾迹的一侧或两侧。这些成分来自船舶尾流中心线附近短发散开尔文波的布拉格散射。在湍流尾迹的边界处, 窄V形尾迹可延伸至水面舰艇后方20 km处, 夹角在2º~3º之间。卫星图像中相关的窄亮线显然是由波长在1 m及以下的短波布拉格散射产生的。它们通常是船舶尾迹图像中最亮的特征, 然而与船尾流的其他部分相比, 相关波浪系统的能量可以忽略不计。

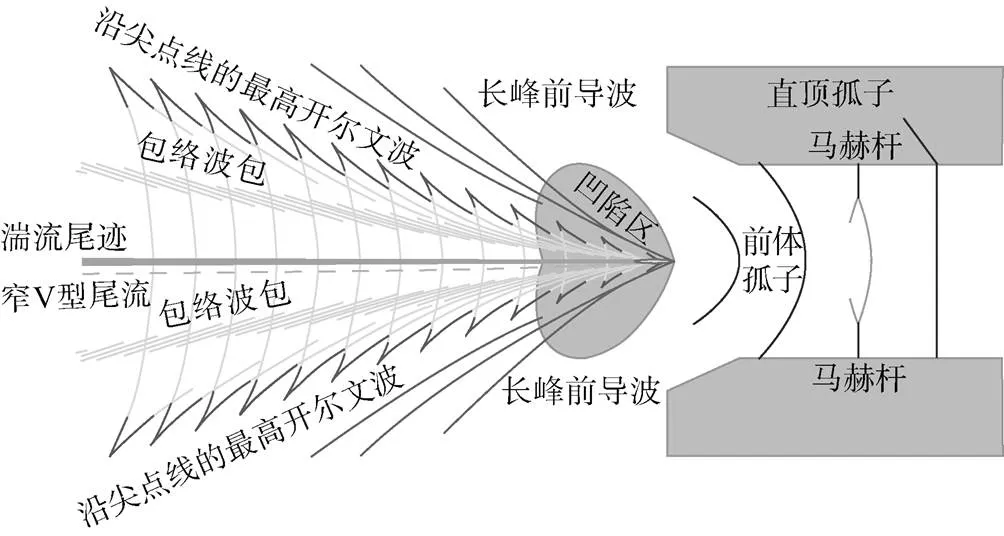
图1 船舶尾流非线性分量示意图

2) 开尔文楔内以及开尔文楔边界处的包络波包[22]: 卫星图像上的另一个V形尾流, 与航行线的平均角度约为10º, 有时可以观测到。在许多情况下, 这一特征可能是由于分米级的布拉格散射、波浪破碎产生的时变表面波和船舶附近的湍流造成。它是由线性发散的开尔文波内干涉射线的镜面散射引起。在许多情况下, 它是一个高度非线性的空间局域波包, 类似于NLS(nonlinear Schrodinger)方程的包络孤子解。这种包经常与跨临界和超临界尾迹相联系。事实上, 在低至0.5的弗劳德数上, 这一点变得很明显。

开尔文尾迹的最高稳定波位于开尔文楔的边界, 经常形成一个调制波包, 其潜在的非线性演化在某些情况下可能是重要的。Akylas利用MNLS(modified nonlinear Schrodinger)方程分析了该包的时间演化和这些线附近潜在的非线性和非定常效应。当船舶突然开始运动时, 波包的远场达到非线性稳定状态。非定常瞬态效应被限制在离船运动的有限区域内。

3) 前体孤子: 根据线性理论可知, 船舶前方没有稳定波存在。这在深水中是完全正确的, 在浅水区也适用于中等速度。然而, 类似于KdV孤子的几乎稳定的孤子扰动经常发生在限制水域内以一定速度航行的船舶前方。

4) 一维上下游的波: 适当的非线性模型考虑了有限振幅效应, 包括向上游传播的孤子(前体孤子)。用()和()分别代表运动表面压力块和地形, 并且F≈1。在随地表压力或地形移动的坐标系中, 长波的水面高度可以用fKdV(fifth order KdV)方程来描述

对于F=1,, 该方程是典型的同伦KdV方程。fKdV方程解的框架仅适用于运动的长波部分, 不能描述船后的短波。它本质上也只包含一个空间维度, 被称为一维情况。

5) 二维孤子[23]: 在相对窄的河道中产生前体孤子的一个显著特征是由二维扰动产生近乎完美的一维上游孤子, 而二维开尔文型尾流通常存在于下游。fKdV模型本质上是一维的, 必然会产生直波峰。Katsis 和Akylas首先克服了这种类型孤子的一维极限。他们分析了临界速度附近的线性色散关系, 导出了表面高度的受迫KP(Kadovtsev-Petviashvili)方程

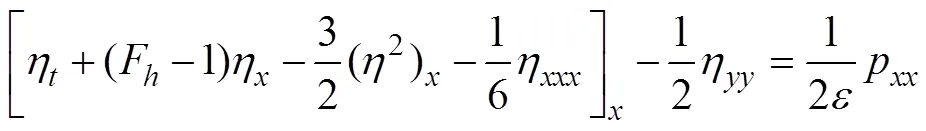
上式描述了由运动压力分布激发的非线性长波的色散、非线性和横向效应。

6) 超临界孔[24]和表面凹陷区[25]: 当弗劳德数增加到F≈1.1~1.2时, 不间断孤子周期性地从船上辐射出去, 从低弗劳德数的破断孤子逐渐过渡到高弗劳德数的破孔。在弗劳德数的一定范围内存在一个几乎规则的孔。如果F≈F+, 这种孔的速度通常比船快。在弗劳德数F>F+时, 形成一个稳定的超临界波系统。辐射孤子和超临界孔在平静水位以上缓慢上升并带有一定质量。在运动扰动的正后方, 河道和无界区域都形成了一个深度几乎一致的更长的凹陷区域。凹陷的范围可能相当大, 与前体孤子覆盖区域的长度相当。它的存在引起了排水型高速船的下沉效应。这种现象是浅水航行的一个特殊特征, 在极端情况下可能成为额外的危险源。

文中仅考虑无量纲KP方程的2个孤子解及其相互作用[26], 因为由3个或更多孤子相互作用产生的结构(尽管在某些条件下远高于由2个相互作用激发的波峰)通常寿命较短[27]。

2 双孤子解

2.1 基本理论

考虑一个非线性偏微分方程

引入因变量的变化

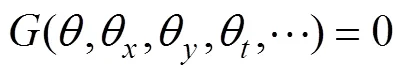
只有Hirota多项式具有以下的性质, 式(3)才能被称为KdV型方程。

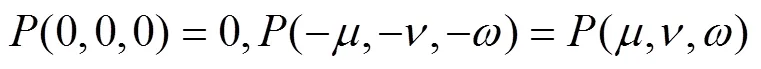
Hirota双线性形式的所有非零解是式(5)的解, 即

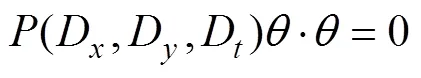
式(4)的变化促使引入算子

2.2 正负相移双孤子解

相位变量中的双孤子解形式[26]为

其中

以下分析仅考虑12≥0的情况, 图2显示了正相移和负相移的双孤子解。

对于系数12的不同值, 有以下2种特殊情况。

1) 当12=0时, 双孤子解表示2个孤子的共振, 给出一个孤子解

对应的孤子称为共振孤子。图3显示了具有共振孤子相位变量中的双孤子解。这种情况可以解释为具有无限相移(即)的双孤子解。

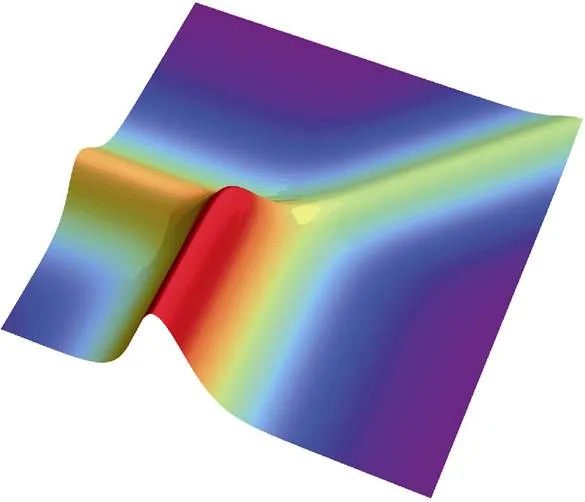
图3 孤子相互作用形成共振孤子

2) 当12=+∞时, 双孤子解是微不足道的。

图4 大的正负相移双孤子解

2.3 相互作用孤子及双孤子解的分解

下面是相互作用孤子更精确的定义, 为此引入函数

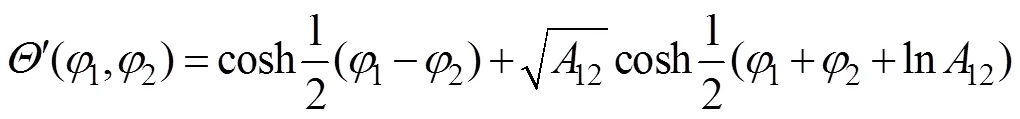
式(12)等价于式(9), 利用式(12)可以导出相位变量中2个孤子解的表达式

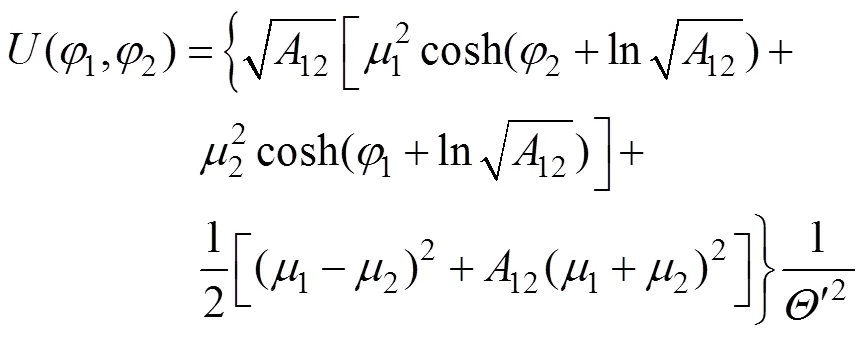
这表明了下面的分解

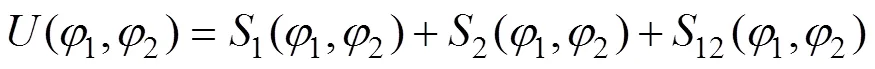
构成式(14)的函数分别为

1,2,12分别对应2个纯孤子和相互作用孤子, 图5和图6显示了这些函数。

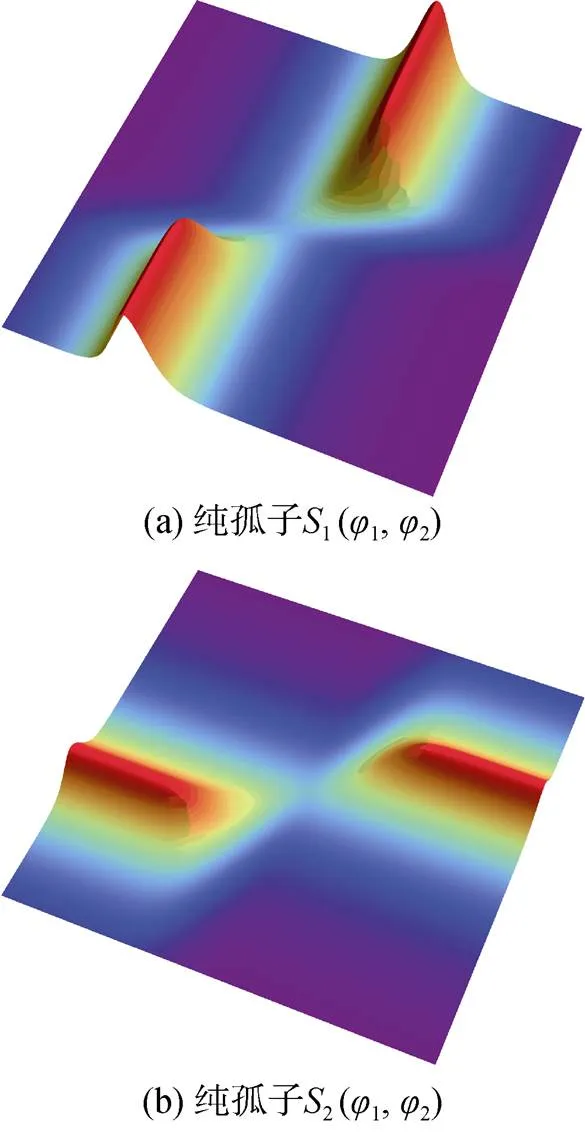
图5 2个纯孤子解

图6 孤子相互作用

3 孤子尾流相互作用的表面高度

浅水区表面重力波的无量纲KP方程

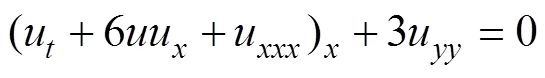
KP方程的双孤子解可以明确地写出来。它是固定模式在实空间中的一致平移, 即=0 时有

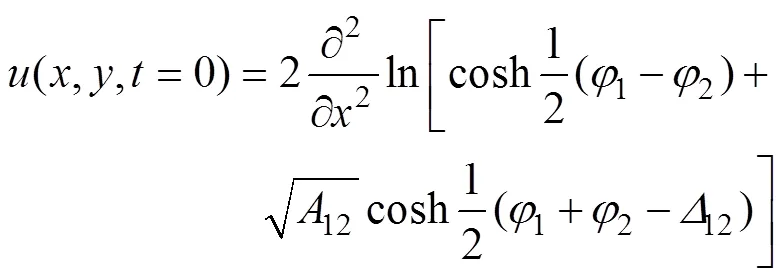
彼得森使用的“几何”方法中孤子相互作用位置[28]如图7所示。负相移情况下, 入射孤子峰的理想模式为实线, 没有相互作用的位置为虚线, 相互作用的位置为粗虚线。值得注意的是, 相互作用孤子的波峰不一定与轴平行, 除非入射孤子的高度相等(波矢的长度相等)。

图7 孤子相互作用位置几何图

理想入射孤子波峰的公共部分长度[28]为

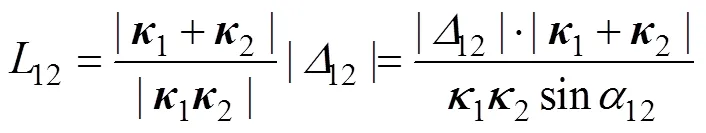
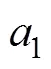
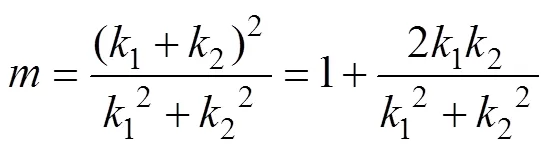
负相移情况下非线性放大系数示意图如图8所示。

由图8可以看出: 当2个入射孤子的振幅相近时,接近于2; 当振幅之差增大时,减小; 当振幅相差很大时,接近于1。

由图9可以看出, 等振幅入射孤子相互作用模型总是相对于一个称为相互作用中心的特定点对称, 并且在一个适当变化的坐标系中静止不变。等振幅入射孤子的振幅高度小于相互作用的表面高度, 并且相互作用的表面高度随着入射孤子振幅高度的增大而增大。当入射孤子的振幅与参考孤子的振幅(相当于相互作用角和临界角之间的差异)相差1%和0.01%时, 相互作用的表面高度大大超过了入射孤子的振幅, 并且相差0.01%比相差1%的相互作用波峰空间范围大。

图9 不同m值的等振幅入射孤子相互作用区域表面高度

由图10可以看出, 非等振幅入射孤子相互作用模型与等振幅入射孤子相互作用模型相比, 对称性和变化趋势大致相同, 但是这种变化趋势不明显。当入射孤子的振幅与参考孤子的振幅相差1%和0.01%时, 其相互作用波峰的空间范围大致与振幅相等时一样大, 这种相互作用主要导致了2种入射孤子波峰的弯曲。

4 孤子尾流相互作用的坡度

实际上, 了解异常陡峭的波浪是否会在何时何地出现是很有价值的, 因为在海上的实际情况中, 造成严重危险的不是波浪的高度, 而是其巨大的坡度。陡峭的孤子相互作用前沿导致产生的波峰高度异常, 这一特征可能是相互作用中心附近的波峰在达到理论最大高度之前频繁破裂的主要原因[14]。高非线性波峰破裂的可能性使近共振相互作用孤子的撞击变得异常危险, 因为破裂过程尤其对船舶有严重威胁。

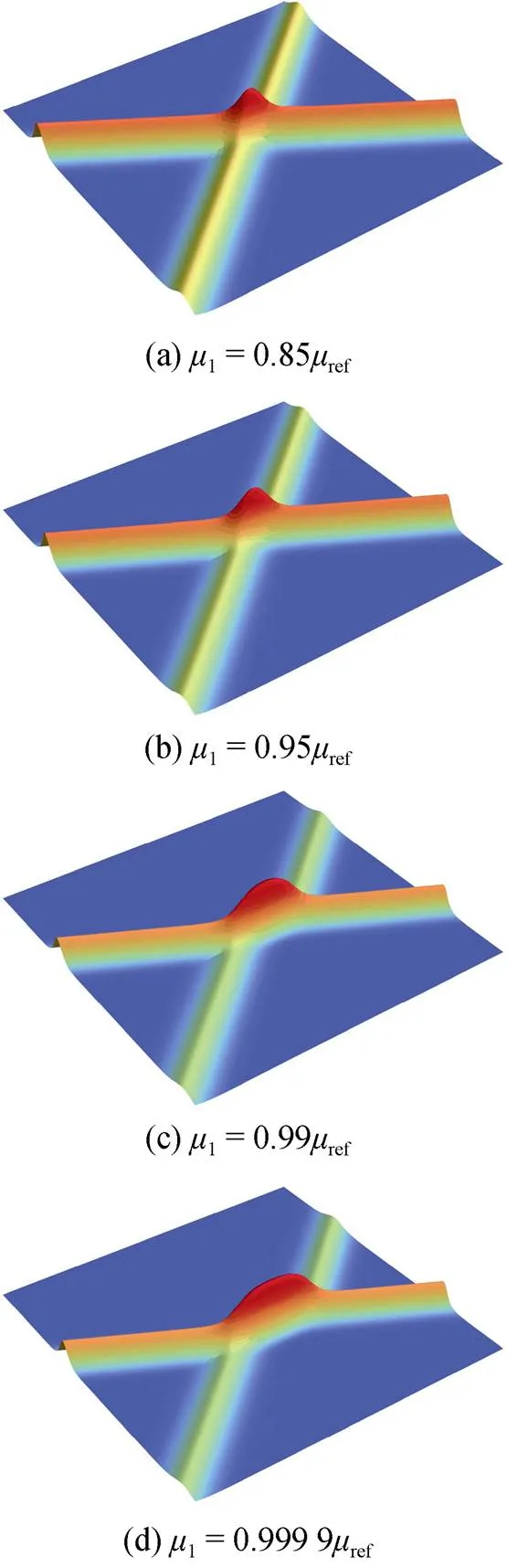
图10 不同m1值的非等振幅入射孤子的相互作用区域表面高度

若波峰与轴方向垂直, KP方程单孤子解的表面高度为

其斜率表达式为

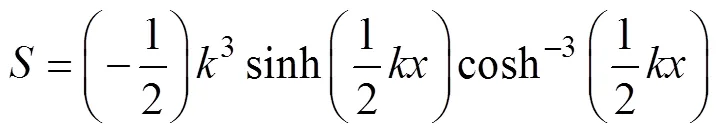
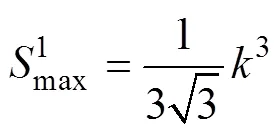
双孤子解的近共振面图表明, 双孤子解的波前最大斜率明显出现在相互作用中心附近, 在该点附近的表面高度为

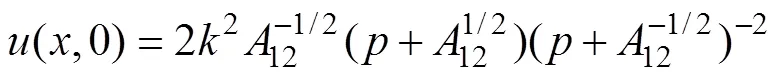
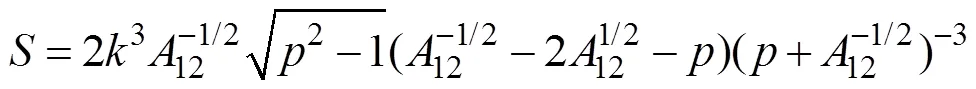
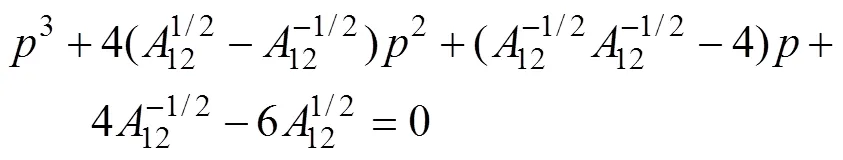
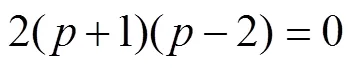
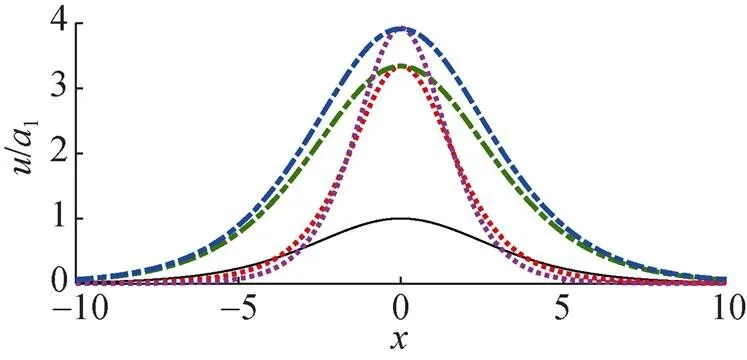
图11 入射孤子和相互作用中心双孤子的不同波峰

由图11可知, 非线性相互作用波峰最高部分的轮廓比入射孤子的轮廓窄, 且值越大, 其比入射孤子的轮廓越窄, 相应的坡度越大。相互作用孤子的波峰沿其传播轴方向具有特定的结构: 沿波峰的传播方向,值越大, 相互作用孤子的轮廓越窄, 坡度越大。

5 结论

1) 在限制水域中, 快速船舶的尾迹最重要的特征是在船舶前方能产生孤立波。孤波高度和斜率的非线性放大可能造成严重的危险。

2) 在正相移情况下, 用Mathematica软件对双孤子解进行分解, 运算和仿真结果表明了双孤子解的波形是各个分解结构的线性叠加。

3) 当入射孤子的振幅与参考孤子的振幅相差1%和0.01%时, 等振幅和非等振幅入射孤子的相互作用区域的表面高度都大大超过了入射孤子的振幅。不同的是, 等振幅入射孤子的振幅与参考孤子的振幅相差0.01%比相差1%的相互作用波峰空间范围大, 而非等振幅入射孤子的这种相互作用主要表现为2种入射孤子波峰的弯曲。

4) 在KP方程的框架中, 孤子相互作用的波峰最高部分的轮廓比入射孤子的轮廓窄, 相互作用孤子的波峰沿其传播轴方向具有特定的结构: 沿波峰的传播方向,值越大, 相互作用孤子的轮廓越窄, 坡度越大。

[1] 张建生, 吕青, 冀邦杰, 等. He-Ne激光通过气幕的特性[J]. 鱼雷技术, 2001, 9(1): 20-23.

[2] 张建生, 王浩, 冀邦杰, 等. 有可能用于鱼雷尾流自导的某些光学特征[J]. 鱼雷技术, 2002, 10(3): 27-31.

[3] 冀邦杰. 光尾流自导中抗干扰技术研究[J]. 鱼雷技术, 2007, 15(1): 17-18, 50.

[4] 张建生, 林书玉, 刘鹏, 等. 船舶尾流气泡幕中的声速[J]. 中国科学(G辑:物理学力学天文学), 2007, 37(6): 783-788.

[5] 张成基. 船舶尾流模拟及感应磁场分布特性[D]. 西安: 西安工业大学, 2018.

[6] 兰青.模拟尾流热特性研究[D].西安: 西安工业大学,2017.

[7] 张建生.尾流的光学特性研究与测量[D].西安: 中国科学院西安光学精密机械研究所,2001.

[8] Tarmo S. Nonlinear Ship Wake Waves as a Model of Rogue Waves and a Source of Danger to the Coastal Environment: A Review[J]. Oceanologia, 2006, 48(S):185-202.

[9] 黄景宁, 徐济仲, 熊吟涛. 孤子:概念、原理和应用[M]. 北京: 高等教育出版社, 2004.

[10] Soomere T. Nonlinear Components of Ship Wake Waves[J]. Applied Mechanics Reviews, 2007, 60(3): 120-138.

[11] Li Y, Sclavounos P D. Three-dimensional Nonlinear Solitary Waves in Shallow Water Generated by an Advancing Disturbance[J]. Journal of Fluid Mechanics, 2002, 470:383-410.

[12] Soomere T, Põder R, Rannat K, et al. Profiles of Waves from High-Speed Ferries in the Coastal Area[J]. Proc. Est. Acad. Sci. Eng., 2005,11(3): 245-260.

[13] Soomere T, Rannat K. An Experimental Study of Wind Waves and Ship Wakes in Tallinn Bay[J]. Proc. Est. Acad. Sci. Eng., 2003, 9(3):157-184.

[14] Jiankang W, Lee T S, Shu C, et al. Numerical Study of Wave Interaction Generated by Two Ships Moving Parallely in Shallow Water[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(15): 2099-2110.

[15] Soomere T, Engelbrecht J. Extreme Elevations and Slopes of Interacting Solitons in Shallow Water[J]. Wave Motion, 2005, 41(2): 179-192.

[16] Osborne A R, Onorato M, Serio M, et al. The Nonlinear Dynamics of Rogue Waves and Holes in Deep-water Gravity Wave Trains[J]. Physics Letters A, 2000, 275(5): 386-393.

[17] Slunyaev A, Kharif C, Pelinovsky E, et al. Nonlinear Wave Focusing on Water of Finite Depth[J]. Physica D: Nonlinear Phenomena, 2002, 173(1): 77-96.

[18] Gusev A V, Lyapidevskii V Y. Turbulent Bore in a Supercritical Flow over an Irregular Bed[J]. Fluid Dynamics, 2005, 40(1): 54-61.

[19] Peterson P, Soomere T, Engelbrecht J, et al. Soliton Interaction as a Possible Model for Extreme Waves in Shallow Water[J]. Nonlinear Processes in Geophysics, 2003, 10(6): 503-510.

[20] 刘杨.舰船尾流气泡幕与异常浪的研究[D]. 西安: 西安工业大学,2016.

[21] Reed A M, Milgram J H. Ship Wakes and Their Radar Images[J]. Annual Review of Fluid Mechanics, 2002, 34(1): 469-502.

[22] Akylas T R , Kung T J . On Nonlinear Wave Envelopes of Permanent form Near a Caustic[J]. Journal of Fluid Mechanics, 1990, 214(1):489-502.

[23] Soomere T, Engelbrecht J. Weakly Two-dimensional Interaction of Solitons in Shallow Water[J]. European Journal of Mechanics B-fluids, 2006, 25(5): 636-648.

[24] Gusev A V, Lyapidevskii V Y. Turbulent Bore in a SuperCritical Flow over an Irregular Bed[J]. Fluid Dynamics, 2005, 40(1): 54-61.

[25] Gourlay T P. Ship Squat in Water of Varying Depth[J]. The International Journal of Maritime Engineering, 2003, 145(a1): 1-8.

[26] Peterson P, Van Groesen E. A Direct and Inverse Problem for Wave Crests Modelled by Interactions of Two Solitons[J]. Physica D: Nonlinear Phenomena, 2000, 141(3): 316-332.

[27] Peterson P, Van Groesen E. Sensitivity of the Inverse Wave Crest Problem[J]. Wave Motion, 2001, 34(4): 391-399.

[28] Soomere T. Interaction of Kadomtsev–Petviashvili Solitons with Unequal Amplitudes[J]. Physics Letters A, 2004, 332(1): 74-81

Study on Nonlinear Wake Interaction

WANG Cheng-ying, ZHANG Jian-sheng

(School of Sciences, Xi’an Technological University, Xi’an 710021, China)

The most important feature of the wakes of fast ships in restricted waters is that solitary waves can be generated ahead of the ship. Using the Korteweg de Vries equation and the sign and auxiliary results of the Hirota bilinear form, this study derives a two-soliton solution with different phase changes. All possible waveforms of the two-soliton solution of the Kadovtsev-Petviashvili(KP) equation for different phase changes and the waveforms of the decomposition structure and linear superposition of the two-soliton solution are obtained using Mathematica. This establishes a foundation for understanding the two-soliton solution of the KP equation, two-soliton interaction, and its morphological characteristics. Based on the two-soliton solution of the dimensionless KP equation, the study simulates the surface height of the interaction region of equal and unequal amplitude incident solitons with standard coordinates. The results show that the amplitude difference between the equal amplitude incident soliton and the amplitude of the reference soliton is 0.01% larger than that of the 1% difference in the space of the interaction peak. The interaction of two incoming solitons with unequal amplitudes results in the bending of their wave humps. The different wave humps of the incoming soliton and two-soliton solution at the center of interaction area are obtained using MATLAB. Finally, the slopes of the interacting solitons are compared by adjusting the parameter. Results show that for a higher value of, the profile of the interacting soliton is narrower and the slope along the propagation direction of the wave crest is greater.

ship wake; two-soliton solution; soliton interaction; surface height; slope

王程英, 张建生. 非线性尾流相互作用研究[J]. 水下无人系统学报, 2020, 28(6): 685-693.

U661.1; O175.29

A

2096-3920(2020)06-0685-09

10.11993/j.issn.2096-3920.2020.06.014

2020-05-12;

2020-07-21.

陕西省教育厅专项科研计划项目(2010JK585); 西安市未央区科技计划项目(201843).

王程英(1993-), 女,在读硕士, 主要研究方向为水下信息光学、光学测试研究.

(责任编辑: 许 妍)