无人艇集群最优协同控制反演

张振华, 李 尧, 俞成浦

无人艇集群最优协同控制反演

张振华, 李 尧, 俞成浦*

(北京理工大学 自动化学院, 北京, 100081)

为实现通过数据驱动学习人为操作下的无人艇集群最优协同控制策略, 文中提出了一种线性二次型闭环微分博弈反演优化算法, 根据观测到的系统最优状态和控制输入轨迹辨识协同策略目标函数。首先, 根据观测到的含加性白噪声的最优系统状态和控制输入轨迹辨识最优反馈矩阵; 然后, 通过求解由纳什平衡充要条件推出的耦合代数黎卡提方程的解来辨识协同策略目标函数。所提出的反演优化算法能够获得满足给定系统状态和控制输入轨迹的最优协同策略目标函数; 同时, 该算法辨识出的目标函数可以用于实现针对特定任务场景的无人艇集群最优协同控制, 并为集群的对抗博弈提供新的思路和解决方案。

无人艇集群; 最优协同控制; 反演优化; 耦合代数黎卡提方程

0 引言

无人艇集群能在复杂海况下执行协同任务, 其在军用和民用领域的应用前景十分广泛。针对给定的任务目标, 无人艇集群的理想行为可以看作是其最优协同控制的结果[1-2]。在实际应用中, 实现最优的协同控制必须有最优的定量协同策略作为具体评价标准, 也就是无人艇集群在任务执行期间的决策和行为应使某些目标函数的值达到最优(一般是最小值)。由于无人艇集群工作环境的复杂性和拓扑连接的多样性, 其最优协同控制策略很难直接采用强化学习等方法试探[3]。一种快速得到最优协同控制目标函数的思路是以“人”为最优参考标准[4], 在某一任务场景下让一组经验丰富的操作人员做出决策进而控制各个无人艇, 并采集无人艇集群的动态信息, 包括无人艇集群的运动状态和每个操作人员对单艘无人艇的控制输入。然后结合采集得到的动态信息和已知的无人艇集群动力学特性, 将人对各无人艇的控制策略反演优化为机器可以理解的目标函数。使用反演优化出的目标函数, 无人艇集群可以在无人的任务场景中自主决策从而实现最优协同控制。这种从行为信息和系统模型出发得到最优协同控制策略的问题一般被称为最优协同控制反演问题。探究最优协同控制反演问题对揭示人类操艇经验的隐性知识有很大帮助, 可推动无人艇集群最优协同控制的研究。

作为无人艇集群最优协同控制的参考对象, 人与人之间协同是在了解任务目标和他人当前情况条件下, 各自做出完成自身当前任务的最优决策。为了使无人艇集群更好地模拟人的协同策略, 即通过辨识得到的模型自主产生的最优协同控制策略与人遥控的策略尽可能吻合, 文中选用纳什最优下的微分博弈模型为辨识模型[5], 设计无人艇集群最优协同控制反演算法来辨识各无人艇目标函数权重矩阵的参数值。由于绝大多数情况下各无人艇在协同过程中能同人一样实时交换所需信息, 所以文中使用闭环微分博弈模型作为辨识模型。因而, 在算法研究中, 无人艇集群的最优协同控制反演可以近似为无人艇集群的闭环纳什最优微分博弈反演优化问题。

针对闭环非合作微分博弈反演问题, 国内外学者已经进行了一些基础性的研究[6-7]。Li等[8]研究了对应于稳态纳什策略的对称耦合代数黎卡提方程, 所提出的并行算法收敛到耦合代数黎卡提方程的非负(正)定稳定解; Priess等[9]提出了一套在连续时间和离散时间情况下寻找时不变线性二次调节器(linear quadratic regulator, LQR)问题的目标函数的技术, 并用于反演人体坐姿控制策略; Rothfuß等[10]以驾驶辅助系统为例, 研究了人机协同背景下如何通过非合作微分博弈反演对人的行为策略建模; Inga等[11]提出了一种方法来寻找在无限时间区间线性二次(linear quadratic, LQ)微分策略中产生相同纳什平衡的所有成本函数, 该方法依赖于耦合矩阵黎卡提方程的重新表述; Molloy等[12]提出了2种基于最小值原理的有限时间开环非线性微分博弈反演算法, 并在2个智能体三维避碰博弈实例中实现较高的辨识精度; Köpf等[13]设计了一种用于离散闭环博弈反演的方法, 并用于球-杠杆模型。

上述研究主要集中于理想博弈模型的反演, 但关于多人协同决策经验的建模与迁移应用还存在欠缺。无人艇集群的最优协同控制反演问题主要体现在有3艘及以上目标函数未知的无人艇参与博弈, 且实际控制决策并非由理想博弈模型产生, 相当于采集的信号与参数逼近最好的理想模型得出的信号间存在固有噪声。文中采用非合作闭环LQ纳什最优微分博弈模型, 给出了无人艇集群基于所反演优化的模型参数自主实现最优协同控制的决策方法, 即反演问题对应的正问题, 并将由该方法生成的轨迹加入噪声以模拟人的实际决策过程, 然后基于约束优化方法对无人艇集群的最优协同控制反演过程进行数值仿真, 得到最接近实际协同控制过程的模型参数, 分析其所反演模型生成的运动和控制轨迹与实际轨迹的误差, 为今后基于无人艇集群最优协同控制真实场景数据的反演与模型迁移研究提供参考。

1 模型建立

1.1 正问题求解

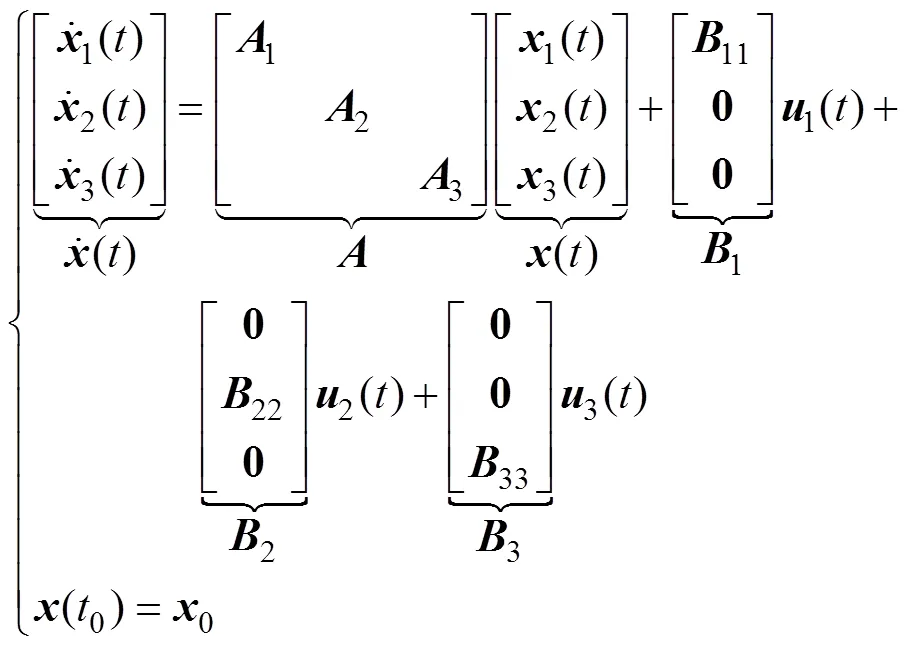
无人艇集群的最优协同控制模型主要体现在最优目标函数与系统动力学特性两方面。为简化计算并满足实时性要求, 文中做出以下假设: 1)不考虑复杂海况和无人艇集群高时滞、大惯性、高度非线性等特征的影响, 无人艇集群系统动力学模型采用可镇定线性时不变(linear time invariant, LTI)微分博弈系统模型; 2) 参考协同控制策略能够采用参数适定的LQ闭环微分博弈目标函数模型近似; 3) 相同初始状态下, 参考协同控制的系统状态和控制输入轨迹与由其反演得到的模型生成的轨迹之差用高斯白噪声近似。

根据上述简化与假设, 得到如式(1)所示无人艇集群系统方程来描述其运动特性

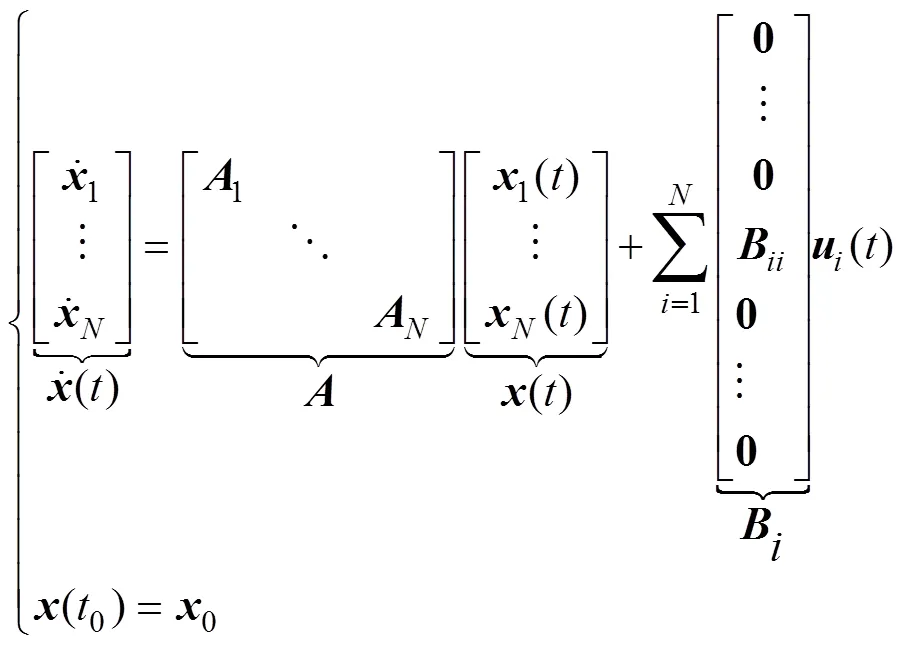
每艘无人艇的控制输入与状态间存在LTI反馈控制率, 即

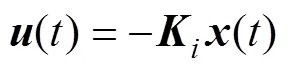
同时定义闭环系统矩阵

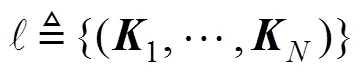
在如图1所示的LQ非合作闭环微分博弈模型中, 每艘无人艇都力图使自身的一个关于式(5)的目标函数

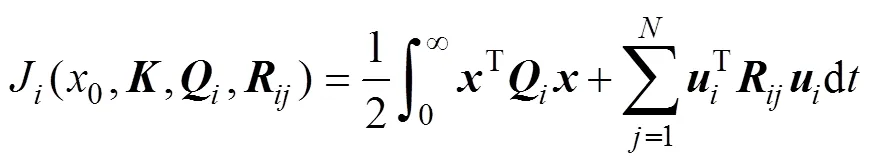
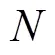
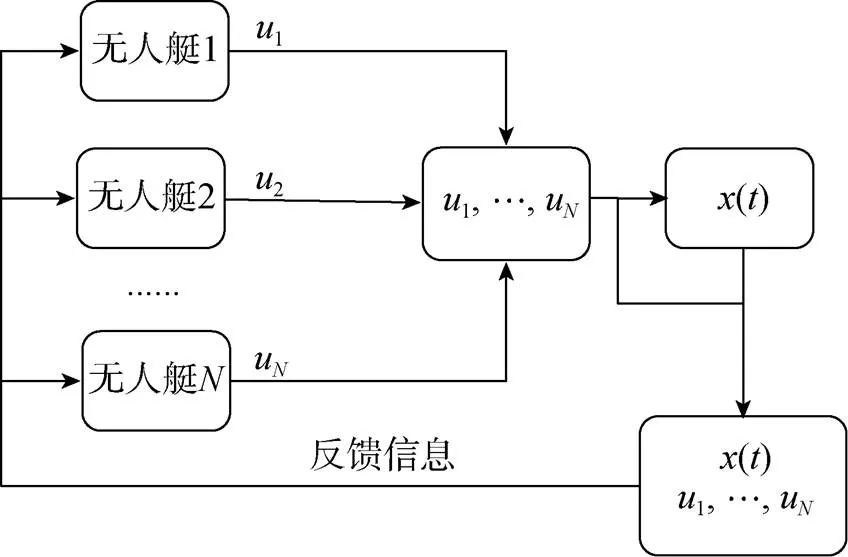
图1 闭环微分博弈框图

在上述模型中, 如果已知其他无人艇的控制率, 对于任意一艘无人艇, 都不能通过调整自身控制率来减小其目标函数值, 否则将被来自其他无人艇博弈性的调整反制, 达到平衡状态, 即

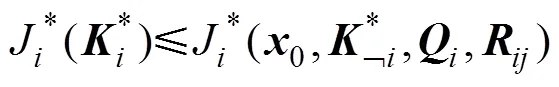
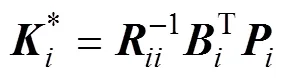
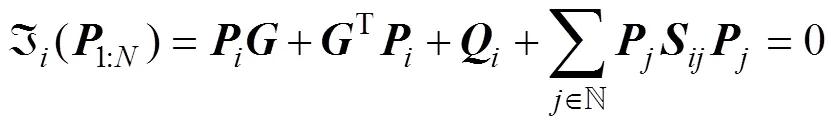
1.2 反演优化算法

为了实现由采集到的无人艇集群运动状态轨迹和每个操作人员对单艘无人艇的控制输入反演, 优化出无人艇集群最优协同控制微分博弈模型, 此部分提出基于耦合黎卡提方程的反演优化算法。

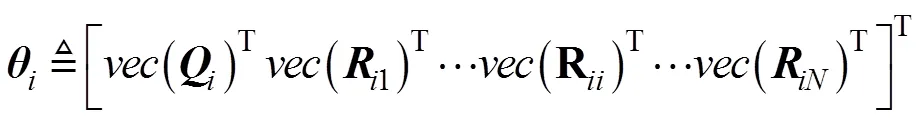
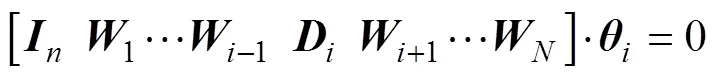
证明: 将式(8)向量化, 得到

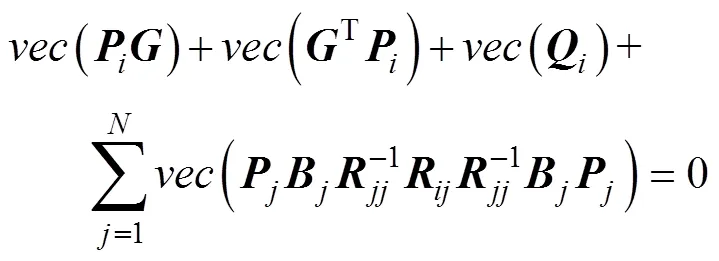
将式(7)代入上式并化简得到

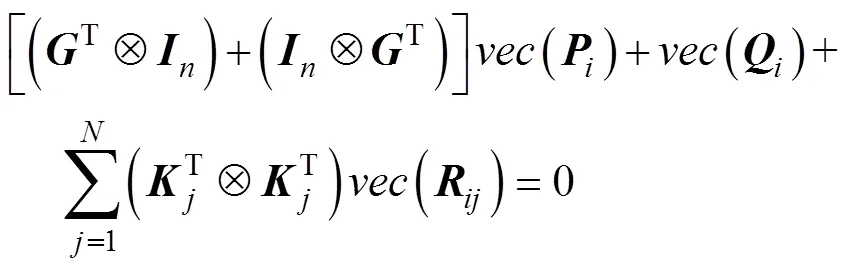
并将式(7)向量化得到

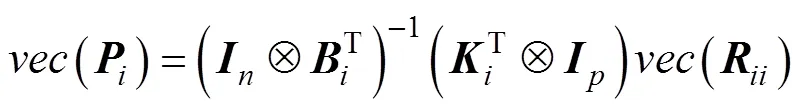
代入式(12)即可得到

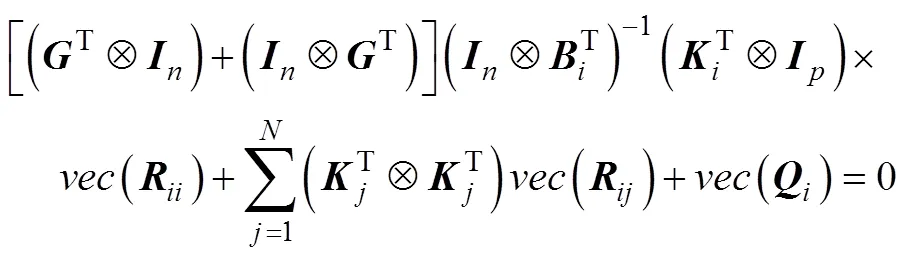
证明完毕。

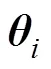
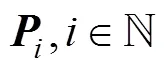
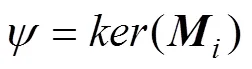
1) 目标函数权重矩阵为对称矩阵

如果假设所有目标函数权重矩阵均为对称矩阵, 则式(10)的未知参数个数为

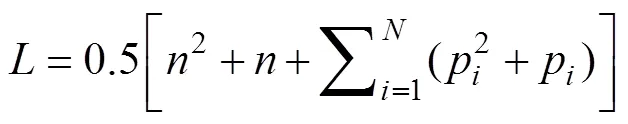
又因为

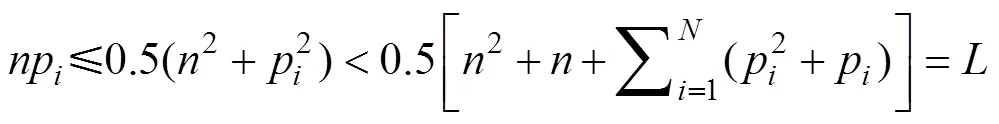
2) 目标函数权重矩阵为对角形式

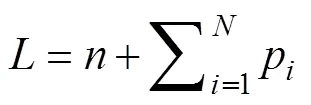
无人艇集群最优协同控制反演优化算法流程如下。

1) 建立采集到的纳什平衡条件下无人艇集群运动状态和每个操作人员对单艘无人艇的控制输入信息模型

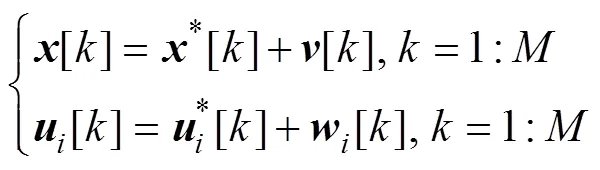
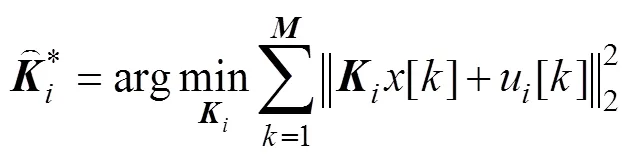
3) 建立反演优化模型。根据式(2)、式(7)和式(19), 对无人艇集群最优协同控制反演优化问题建立如下优化模型

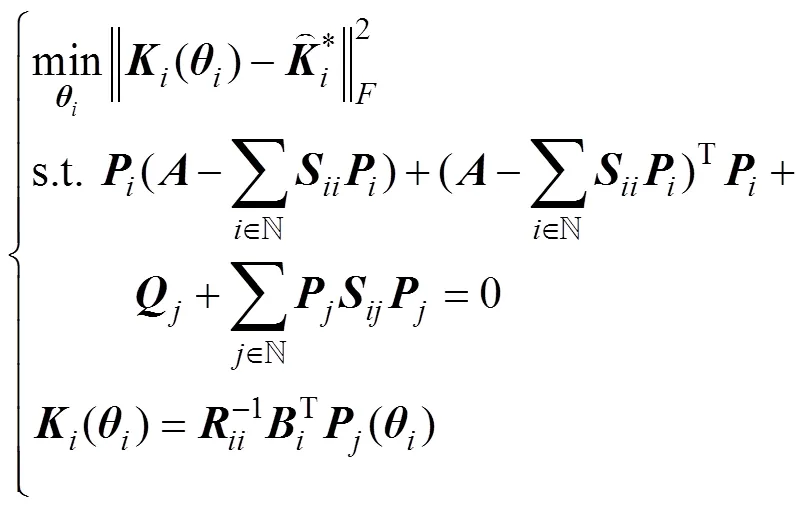
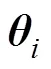
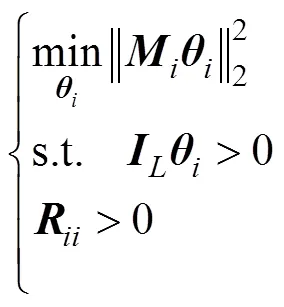
通过计算无人艇集群系统状态真实值与预测值之间的相对误差来验证其准确性

2 仿真结果与分析

通过数值仿真验证文中所提算法的有效性和准确性。

为了便于说明, 以图2所示的3艘无人艇协同执行补充补给任务(图中: 中间为补给船; 三角形的3个顶点为执行任务的无人艇)为例。将此3艘无人艇系统动态方程简化为

用线性二次型微分博弈协同决策目标函数来近似无人艇执行协同任务过程中的控制策略。然后通过采集在执行协同任务过程中系统最优状态和各无人艇控制输入轨迹辨识协同策略目标函数

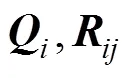
首先求解式(24), 并将得到的系统状态和控制输入轨迹作为观测到的人为操作下无人艇集群系统最优状态和各无人艇最优控制输入。然后, 使用所求得的最优状态量和控制输入量进行反演优化。最后, 根据辨识得到的协同策略目标函数参数再次求解式(24), 得到系统状态和各无人艇控制输入轨迹, 并通过式(22)验证算法的相对误差水平。

现有文献中并没有能确保式(24)所表示的正向微分博弈问题一定收敛的算法, 因此在仿真中仅统计求解正向问题收敛的算法, 来验证所提算法的有效性。

文中实例包含100组正向问题收敛情况下的数值试验结果。所获得的系统状态预测相对误差分布和统计直方图分别如图3和图4所示。

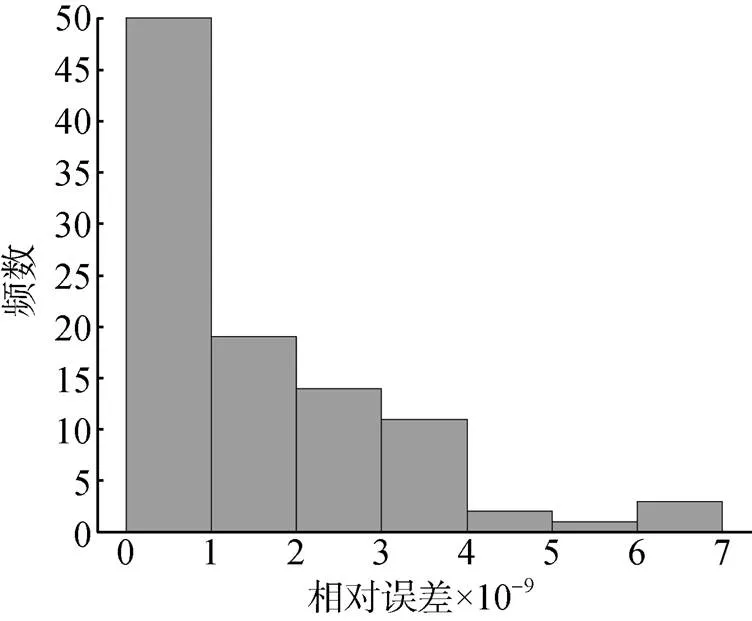
图4 无噪声条件下相对误差统计直方图

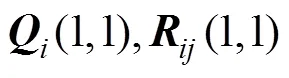
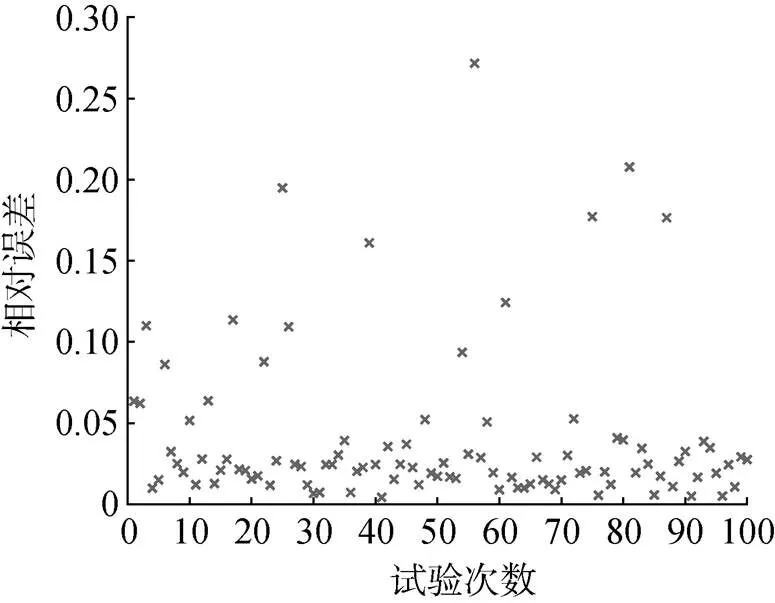
图5 30 dB噪声条件下相对误差分布图

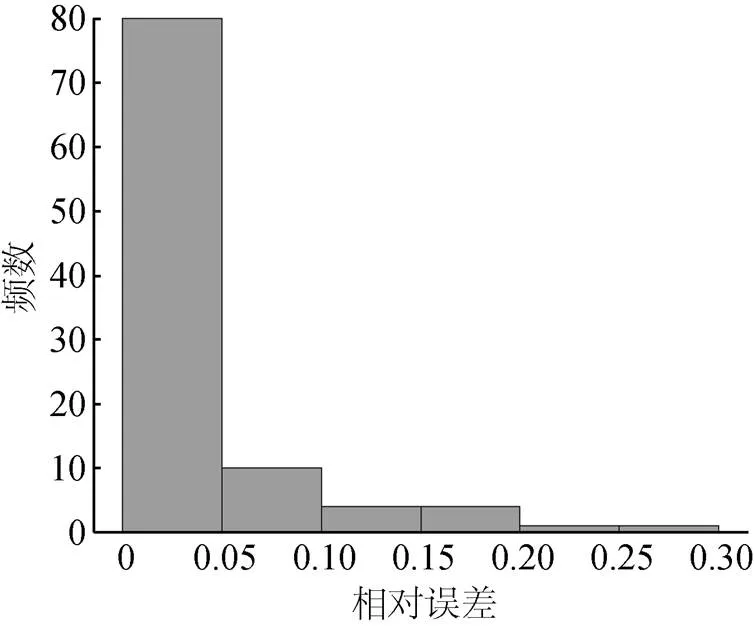
图6 30 dB噪声条件下相对误差统计直方图

3 结束语

文中提出了一种无人艇集群最优协同控制反演优化算法。该算法通过反演优化线性二次型微分博弈问题的协同策略目标函数权重矩阵来学习无人艇集群最优协同控制策略。此外, 该算法构建了一个双层优化的反演优化模型, 并充分利用了线性二次型微分博弈问题达到纳什平衡时的耦合代数黎卡提方程的性质, 将双层优化模型转化为简单的二次型规划问题, 以实现快速求解。

文中所使用的无人艇集群系统方程是近似的线性方程, 且在噪声干扰下反演优化算法精度不高。后续要针对更符合实际的非线性系统方程展开无人艇集群的最优协同控制反演优化算法研究, 并提升算法的鲁棒性。

[1] Carvalhosa S, Pedro Aguiar A, Pascoal A. Cooperative Motion Control of Multiple Autonomous Marine Vehicles: Collision Avoidance in Dynamic Environments[C]//Pro- ceedings of the 7th IFAC Symposium on Intelligent Autonomous Vehicles 2010. Lecce, Italy: IFAC, 2010: 282-287.

[2] Pedro Aguiar A, Almeida J, Bayat M, et al. Cooperative Control of Multiple Marine Vehicles: Theoretical Challenges and Practical Issues[C]//Proceedings of the 8th IFAC International Conference on Manoeuvring and Control of Marine Craft. Guarujá, Brazil: IFAC, 2009: 412- 417.

[3] Wang Y C, Fu H X, Liu F M. Ship Speed Control Method Based on Fuzzy-Cerebellar Model Articulation Controller[C]//Proceedings of the 31st Chinese Control Conference. Hefei, China: CCC, 2012: 4396-4399.

[4] Aza N A, Shahmansoorian A, Davoudi M. From Inverse Optimal Control to Inverse Reinforcement Learning: A Historical Review[J]. Annual Reviews in Control, 2020, 50: 119-138.

[5] Basar T, Olsder G J. Dynamic Noncooperative Game Theory[M]. London: Academic Press, 1999.

[6] Mohajerin Esfahani P, Shafieezadeh-Abadeh S, Hanasusanto G A, et al. Data-driven Inverse Optimization With Imperfect Information[J]. Mathematical Programming, 2018, 167(1): 191-234.

[7] Zhang H, Li Y, Hu X. Inverse Optimal Control for Finite-Horizon Discrete-time Linear Quadratic Regulator Under Noisy Output[C]//2019 IEEE 58th Conference on Decision and Control(CDC). Nice, France: IEEE, 2020.

[8] Li T Y, Gajic Z. Lyapunov Iterations for Solving Coupled Algebraic Riccati Equations of Nash Differential Games and Algebraic Riccati Equations of Zero-Sum Games[M]// New Trends in Dynamic Games and Applications. Boston: Birkhäuser Boston Inc., 1995.

[9] Priess M C, Conway R, Choi J, et al. Solutions to the Inverse LQR Problem with Application to Biological Systems Analysis[J]. IEEE Transactions on Control Systems Technology, 2015, 23(2): 770-777.

[10] Rothfuß S, Inga J, Köpf F, et al. Inverse Optimal Control for Identification in Non-Cooperative Differential Games[J]. IFAC-Papers on Line, 2017, 50(1): 14909-14915.

[11] Inga J , Bischoff E , Molloy T L , et al. Solution Sets for Inverse Non-Cooperative Linear-Quadratic Differential Games[J]. IEEE Control Systems Letters, 2019, 3(4): 871- 876.

[12] Molloy T L, Inga J, Flad M, et al. Inverse Open-Loop Noncooperative Differential Games and Inverse Optimal Control[J]. IEEE Transactions on Automatic Control, 2019, 65(2): 897-904.

[13] Köpf F, Inga J, Rothfuß S, et al. Inverse Reinforcement Learning for Identification in Linear-Quadratic Dynamic Games[J]. IFAC-Papers on Line, 2017, 50(1): 14902- 14908.

Inverse Optimal Cooperative Control for Unmanned Surface Vessel Cluster

ZHANG Zhen-hua, LI Yao, YU Cheng-pu*

( School of Automation, Beijing Institute of Technology, Beijing 100081, China)

To realize an optimal cooperative control strategy of unmanned surface vessel(USV) clusters under artificial control through data-driven learning, a linear quadratic closed-loop differential game inverse optimization algorithm is proposed. The algorithm can identify the cooperative strategy objective function according to the optimal system state and control input trajectories. In this study, an optimal feedback matrix is first identified based on the observed optimal system state and control input trajectories with additive white noise. The cooperative strategy objective function is then identified after solving the coupled algebraic Riccati equations derived from the necessary and sufficient conditions for Nash equilibria.The proposed inverse optimization algorithm can obtain the optimal cooperative strategy objective function to satisfy the given system state and control input trajectories. The objective functions identified by the inverse optimization algorithm can then be used to achieve an optimal cooperative control of USV clusters for specific task scenarios and provide new ideas and solutions for cluster adversarial games.

unmanned surface vessel(USV) cluster; optimal cooperative control; inverse optimization; coupled algebraic Riccati equations

张振华, 李尧, 俞成浦. 无人艇集群最优协同控制反演[J]. 水下无人系统学报, 2020, 28(6): 611-617.

TJ630; U664.82; TP273.1

A

2096-3920(2020)06-0611-07

10.11993/j.issn.2096-3920.2020.06.004

2020-09-04;

2020-10-16.

国家自然科学基金重大项目课题(61991414).

俞成浦(1984-), 男, 博士, 教授, 主要研究方向为系统辨识与机器学习、分布式优化与控制、无线传感器网络与室内定位.

(责任编辑: 陈 曦)