基于分数阶傅里叶变换的双雷齐射主动自导方法

蒋 帅, 樊书宏, 郝保安

基于分数阶傅里叶变换的双雷齐射主动自导方法

蒋 帅, 樊书宏, 郝保安

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)

针对双雷齐射中可能产生的两雷相互干扰问题, 文中提出了一种基于分数阶傅里叶变换的双雷齐射主动自导方法。两雷通过分别发射不同调频斜率的线性调频(LFM)信号, 并利用分数阶傅里叶变换对LFM信号的聚焦特性, 以实现双雷回波信号的分离检测。在此基础上, 提出了双雷齐射目标检测的总体方案, 并进一步分析了影响目标参数估计结果的主要因素。不同信噪比条件下的仿真试验结果表明, 利用分数阶傅里叶变换可有效实现双雷齐射目标检测, 具有较强的抗干扰能力, 且双雷基本可工作于同一频段, 无需分频段使用。该方法可对双雷齐射条件下的主动自导提供参考。

鱼雷; 双雷齐射; 分数阶傅里叶变换; 主动自导; 目标检测

0 引言

鱼雷作为海洋战争中的主战武器, 在打击水中各类舰艇目标中发挥着重要作用。其中, 鱼雷自导是鱼雷实现水下自动寻的和精确制导的关键技术[1]。鱼雷主动发射探测脉冲信号, 并接收目标回波, 通过对回波信号的实时处理, 实现目标信号检测以及目标参数解算等自导功能。

双雷齐射是鱼雷重要的作战使用方式之一, 通过采用双雷齐射可在一定程度上提高目标探测能力与命中概率, 它能覆盖较大的目标机动区域和散布误差, 使目标落入自导搜索扇面的可能 性增大[2]; 相对于连射, 齐射能在较短的时间内完成射击准备, 在相同阵位上获得更高的命中概率或在更远的射击阵位上获得相同的命中概率[3], 从而有效提高对目标的探测和毁伤能力。但双雷齐射情况下, 由于同一区域2条鱼雷的自导系统同时工作, 其中一条鱼雷的发射信号经目标反射产生的回波可能被另一条鱼雷的自导系统接收, 出现两雷相互干扰的问题。因此, 双雷齐射条件下抗互扰已经成为各鱼雷自导的重要性能指标。双雷齐射态势如图1所示。

图1 双雷齐射示意图

图1中, 齐射的双雷A和B同时对于同一目标区域进行目标搜索, 这种情况下, 雷A发射信号经目标反射产生的回波信号可能被雷B自导系统接收, 导致雷B误以为是自身发射信号产生的目标回波, 从而对目标的检测和参数估计产生错误, 即对雷B自导目标跟踪形成了干扰; 同样, 雷B发射信号的目标回波也可能被雷A接收并正常处理, 对雷A自导目标检测和跟踪形成干扰。一旦出现相互干扰, 两雷的探测逻辑将会变得混乱, 无法实现对真实目标的有效探测、参数估计、正常追踪和攻击[4]。

目前主要采用两雷划分不同子带并分别工作于不同频段的方式来避免互扰。但这样可能存在2方面问题: 一是为了适应双雷齐射, 每条鱼雷自导必须同时具备2个不同工作频段, 而实际使用中工作带宽受到限制, 只能工作于其中某一个特定频段(雷A或雷B), 不能充分发挥最大带宽能力; 二是随着当今鱼雷宽带自导技术的快速发展和普遍应用, 采用划分不同子带的方式, 在声学装置等总带宽有限条件下, 难以满足两雷均工作于较大带宽的自导需求。

文中提出了一种基于不同斜率调频信号分数阶傅里叶变换(fractional Fourier transform, FRFT)的双雷齐射自导方法, 即利用FRFT对线性调频(linear frequency modulation, LFM)信号调频斜率的敏感特性, 实现鱼雷主动自导对目标回波LFM信号的聚焦检测。双雷齐射情况下, 两雷分别发射不同调频斜率的LFM信号, 接收目标回波并进行FRFT, 在变换域分别根据各自调频斜率进行目标回波信号检测, 可有效实现双雷目标回波信号分离, 避免双雷目标回波相互干扰。这样, 双雷基本可工作于同一频段, 无需分频段使用。

1 分数阶傅里叶变换

1.1 基本定义和性质

FRFT的研究最早见于1929年Wiener[5]的研究工作, 但直到1993年Almeida[6]指出FRFT可理解为时频平面的旋转、1996年Ozaktas等[7]提出快速离散算法后, 对FRFT的研究才逐渐由光学领域拓展到信号处理领域[8-9]。

FRFT的定义可从线性积分变换的角度给出

1.2 离散计算和归一化处理

在实际工程应用时, 大多数处理的是离散信号, 根据Ozaktas的采样型离散FRFT算法, 离散时域信号的分数阶傅里叶域表示为

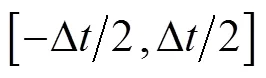
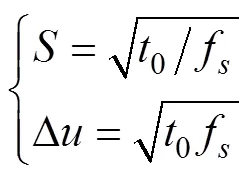
2 基于FRFT的鱼雷主动自导目标检测

2.1 目标检测及参数估计

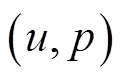
图2 信号检测流程图

假设鱼雷发射信号为

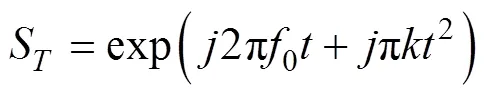
则接收的目标回波信号[11]可表示为

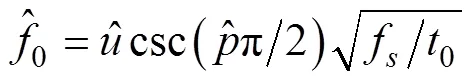
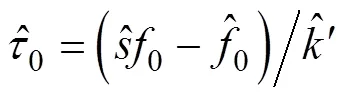
其中

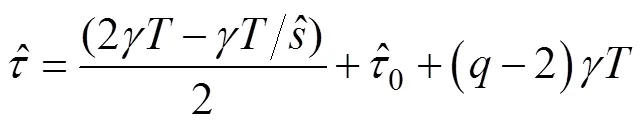
2.2 仿真验证

图3 目标回波信号波形

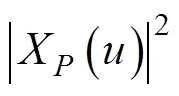
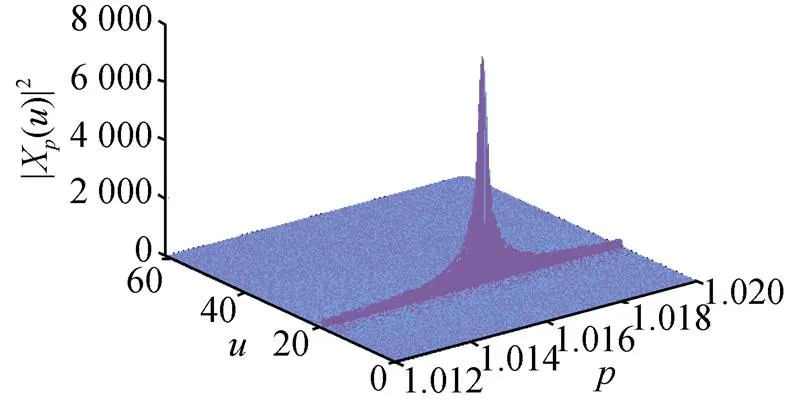
图4 目标回波信号检测结果

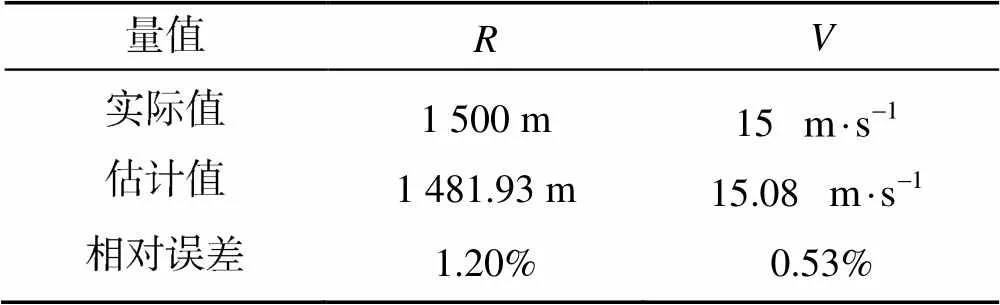
表1 回波检测参数估计值与真实值对比

仿真结果显示, 该方法能够完成目标信号的检测, 且参数估计值与真实值误差较小, 是可行的。

3 双雷齐射抗互扰方法

3.1 总体方案

利用FRFT对LFM信号调频斜率的聚焦特性, 可将具有不同调频斜率的两雷回波信号分离检测, 总体方案如图5所示。

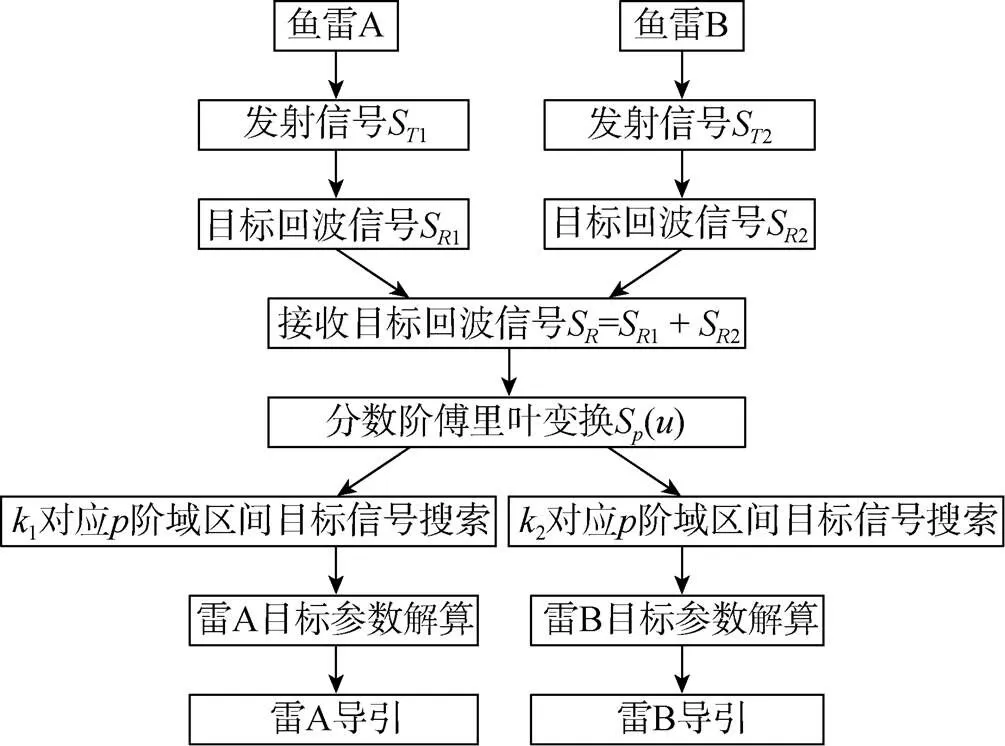
图5 双雷齐射抗互扰总体方案

图5中, 雷A自导系统发射信号S1, 遇到目标后产生回波信号S1; 同理, 雷B自导系统发射信号S2, 遇到目标后产生回波信号S2, 则双雷均接收到的目标回波信号为S=S1+S2, 此时会有互扰的影响, 对接收信号S做FRFT得到S()。

利用不同调频斜率的LFM信号聚焦在不同分数阶傅里叶域的特性, 雷A在1对应的分数阶域最优区间展开搜索, 雷B可在2对应的分数阶域最优区间展开搜索, 即可得到各自自导发射信

号对应的目标回波信号, 进行参数解算后, 便可进行下一步的导引。

3.2 双雷目标回波信号模型及检测方法

假设雷A发射信号为

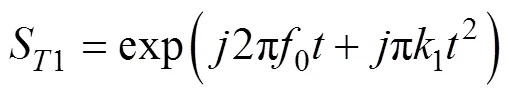
则有目标回波信号

同理, 若雷B发射信号

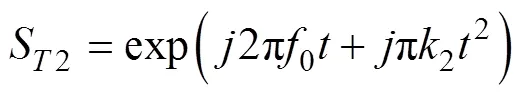
则其目标回波信号为

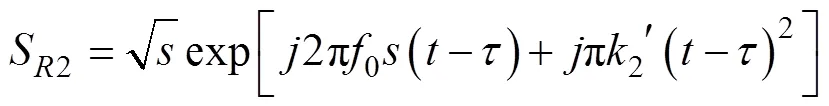
加入噪声后, 则双雷接收到的目标回波信号为

利用两雷调频斜率差异导致的回波信号能量聚焦阶数不同, 各雷在回波信号检测时, 选择不同的阶数区间进行搜索, 便可将两回波信号分离, 进而得各自发射信号对应的目标回波信号, 而后按照上章所述方法便可实现对相应参数的估计。

3.3 双雷抗互扰方法仿真

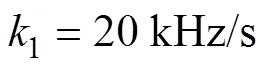
图6 双雷回波信号检测结果

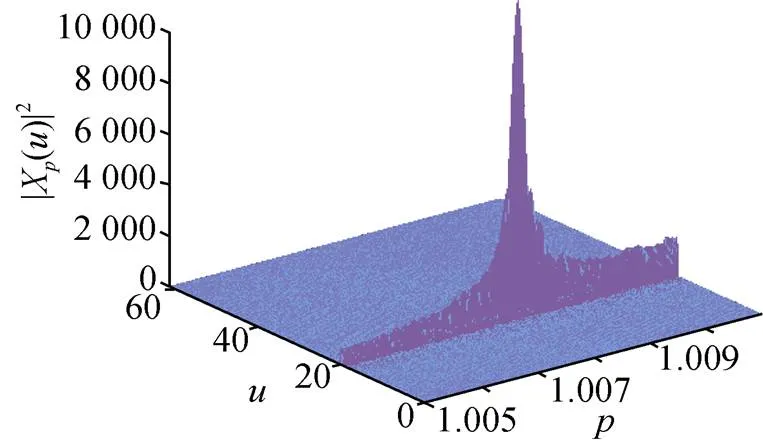
图7 雷A回波信号检测结果

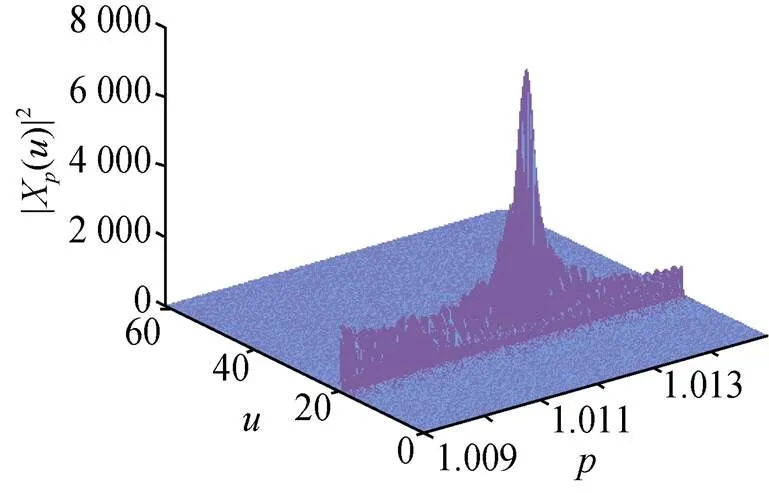
图8 雷B回波信号检测结果

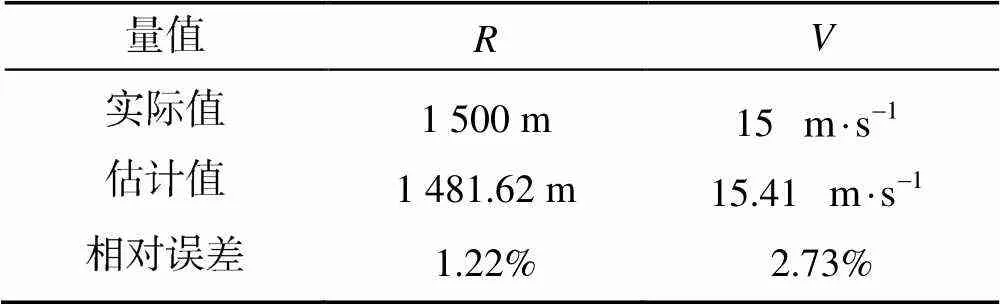
表2 雷A回波检测参数估计值与真实值对比

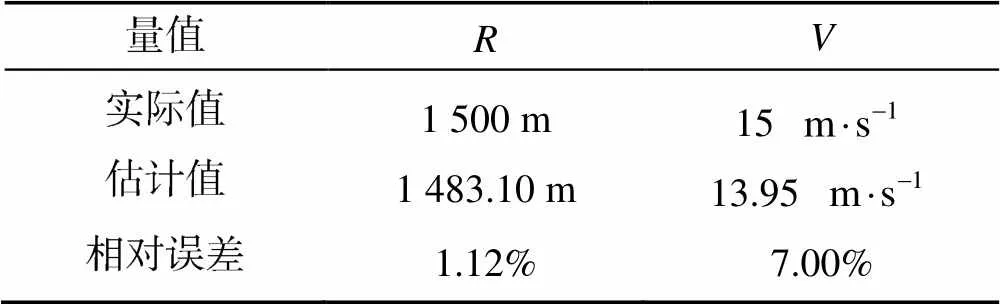
表3 雷B回波检测参数估计值与真实值对比

仿真结果显示, 该方法能够实现双雷回波分离检测, 且参数估计值与真实值相差较小, 证明了方法的可行性。

4 目标参数估计影响因素

4.1 调频斜率

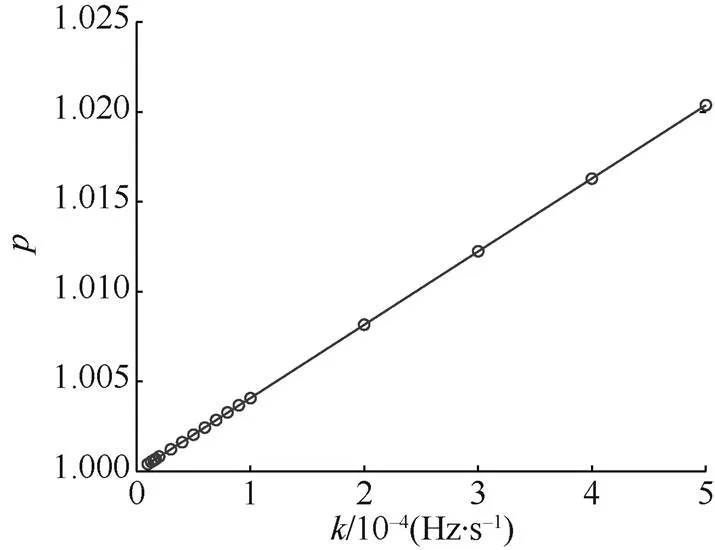
图9 不同调频斜率下聚焦阶数估计值

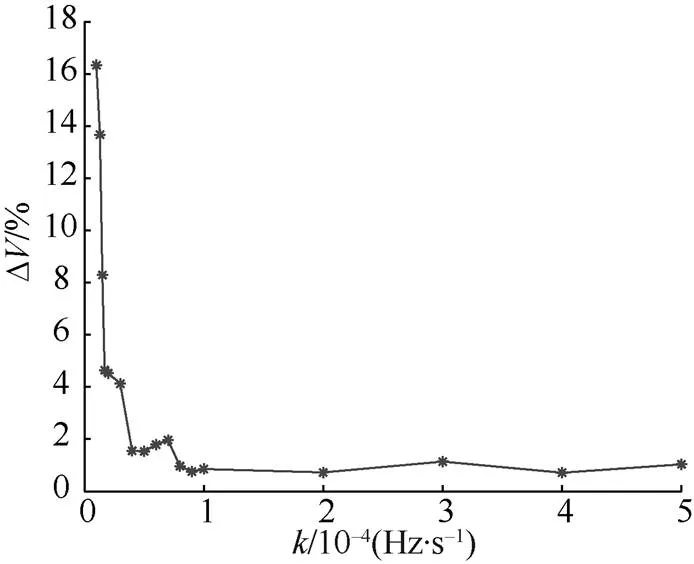
图10 不同调频斜率下相对速度估计误差

图11 不同调频斜率下的目标距离估计误差

4.2 信噪比

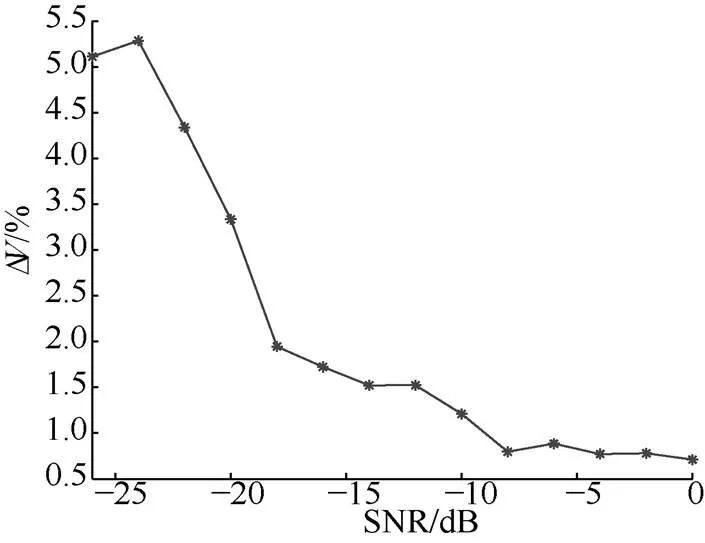
图12 不同信噪比下相对速度估计误差

图13 不同信噪比下目标距离估计误差

图14 SNR= –27时回波信号搜索图

仿真结果表明, 调频斜率较大时, 目标参数估计值更接近于真实值, 且该方法具有较强的抗噪性, 可在很低的SNR下仍具有较好的检测性能。

5 结束语

针对鱼雷双雷齐射主动自导过程中的互扰问题, 提出了一种新的基于FRFT的抗互扰方法, 并对其工作原理和实现过程进行了详细的阐述。在点目标回波模型下, 对单目标的回波信号进行了仿真验证, 对处于噪声环境下的回波信号进行了抗干扰能力的检验, 并进一步对双雷回波信号抗互扰的解决方法进行了仿真验证, 最后对影响参数估计的一些因素进行了量化分析。仿真结果表明, 该方法能够完成两雷回波信号的分离, 实现了两雷对各自回波信号的正确检测与参数估计, 并有着较强的抗干扰能力, 具有可行性和实用价值, 可为双雷齐射主动自导的进一步研究提供参考意义。后续将在此基础上, 针对多分量信号FRFT能量谱相互遮蔽条件下的分离检测问题开展深入分析研究, 进一步提高对工程应用环境的适应性。

[1] 周德善. 鱼雷自导技术[M]. 北京: 国防工业出版社. 2009.

[2] 姜凯峰, 周明, 葛津华. 舰载反鱼雷鱼雷齐射作战能力研究[J]. 舰船科学技术, 2010, 32(11): 64-68. Jiang Kai-feng, Zhou Ming, Ge Jin-hua. Research on Operational Capability of Shipboard Anti-torpedo Torpedo[J]. Ship Science and Technology, 2010, 32(11): 64-68.

[3] 刘影, 周明, 高勇. 声自导鱼雷互扰问题初探[J]. 舰船科学技术, 2006, 28(4): 58-60.Liu Ying, Zhou Ming, Gao Yong. On Mutual Conductance of Acoustic Torpedo[J]. Ship Science and Technology, 2006, 28(4): 58-60.

[4] 张静远, 王鹏. 声自导鱼雷双雷齐射有关技术与战术问题分析[J]. 鱼雷技术, 2013, 21(4): 299-305.Zhang Jing-yuan, Wang Peng. Technical and Tactical Analysis of Two-Torpedo Salvo for Acoustic Homing Torpedo[J]. Torpedo Technology, 2013, 21(4): 299-305.

[5] Wiener N. Hermitian Polynomials and Fourier Analysis[J]. Journal of Mathematics Physics MIT, 1929, 18: 70-73.

[6] Almeida L B. The Fractional Fourier Transform and Time-frequency Representations[J]. IEEE Trans. Signal Processing, 1994, 42(11): 3084-3091.

[7] Ozaktas H M, Arikan, Kutay M A, el al. Digital Computation of the Fractional Fourier Transform[J]. IEEE Trans. Signal Processing, 1996, 44(9): 2141-2150.

[8] Ozaktas H M. The Fractional Fourier Transform with Application in Optics and Signal Processing[M]. New York: John Wiley & Sons, 2001: 117-183.

[9] Chen Y L, Guo L H, Gong Z X. The Concise Fractional Fourier Transform and Its Application in Detection and Parameter Estimation of the Linear Frequency-modulated Signal[J]. Chinese Journal of Acoustics, 2017(1): 70-86.

[10] 陶然, 邓兵, 王越. 分数阶傅里叶变换及其应用[M]. 北京: 清华大学出版社, 2009.

[11] 谢砚同, 彭圆, 张风珍. 基于分数阶傅里叶变换的水下目标速度估计[J]. 数字海洋与水下攻防, 2018, 1(3): 75-80.Xie Yan-tong, Peng Yuan, Zhang Feng-zhen. Underwater Target Velocity Estimation Based on Fractional Fourier Transform[J]. Digital Ocean & Underwater Warfare, 2018, 1(3): 75-80.

[12] 赵兴浩, 邓兵, 陶然. 分数阶傅里叶变换数值计算中的量纲归一化[J]. 北京理工大学学报, 2005, 25(4): 360-364.Zhao Xing-hao, Deng Bing, Tao Ran. Dimensional Normalization in the Digital Computation of the Fractional Fourier Transform[J]. Transactions of Beijing Institute of Technology, 2005, 25(4): 360-364.

[13] Yan M, Yan K. FRFT Based on Joint Estimation Time Delay and Radial Velocity of Underwater Target[C]//2010 3th International Congress on Image and Signal Processing, Yantai: CISP, 2010．

[14] 马艳, 罗美玲. 基于分数阶傅里叶变换水下目标距离及速度的联合估计[J]. 兵工学报, 2011, 32(8): 1030-1035. Ma Yan, Luo Mei-ling. FRFT-based Joint Range and Radial Velocity Estimation of Underwater Target[J]. Acta Armamentarii, 2011, 32(8): 1030-1035.

1. 杨向锋, 熊淑贞, 石磊. 声自导鱼雷目标跟踪误差仿真与分析[J]. 水下无人系统学报, 2020, 28(5).

2. 唐波, 谭思炜, 张静远. 基于自适应噪声对消的鱼雷电磁引信抗雷内干扰方法[J]. 水下无人系统学报, 2020, 28(3).

3. 张方方, 李文哲, 董晓明, 等. 噪声干扰器作用下反潜鱼雷主动自导性能数值分析[J]. 水下无人系统学报, 2020, 28(1).

4. 赵艾奇, 王戈, 孙建, 等. 基于目标舷别判断的火箭助飞鱼雷射击方法[J]. 水下无人系统学报, 2019, 27(4).

5．张俊, 蒋继军, 康文钰, 等. 基于声对接耦合的水下高速航行器全弹道仿真测试方法[J]. 水下无人系统学报, 2019, 27(3).

6．赵世平, 毕凤阳, 卢丙举, 等. 单筒多细长体航行器水下齐射载荷特性仿真[J]. 水下无人系统学报, 2019, 27(1).

7．邓新文, 朱文振, 谢勇. 潜艇转向旋回防御主动声自导鱼雷的战术意义与作战运用[J]. 水下无人系统学报, 2019, 27(1).

8．寇祝, 任磊, 孙庆声. 反蛙人杀伤弹人工散布射击方法仿真[J]. 水下无人系统学报, 2018, 26(6).

9．孙常存, 袁鹏, 王旅. 自航式声诱饵对抗下的反潜助飞鱼雷射击效率建模与仿真[J]. 水下无人系统学报, 2018, 26(6).

10．杨绪升, 尹文进. 基于潜射自导鱼雷射击优化模型的发现概率仿真计算[J]. 水下无人系统学报, 2018, 26(6).

11．李华, 张静远. 声自导鱼雷二次转角作战使用方法[J]. 水下无人系统学报, 2018, 26(4).

Two-Torpedo Salvo Active Homing Method Based on Fractional Fourier Transform

JIANG Shuai, FAN Shu-hong, HAO Bao-an

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China)

A two-torpedo salvo can effectively improve hit probability, but it may cause mutual interference problems. Therefore, a two-torpedo salvo active homing method based on fractional Fourier transform is proposed in this study. The echo signals of two torpedoes can be separated and detected by transmitting linear frequency modulation (LFM) signals at different chirp rates and by applying the focus characteristics of the fractional Fourier transform to those LFM signals. Accordingly, a general scheme for two-torpedo salvo target detection is proposed, and the main factors that affect the target parameter estimation results are further analyzed. Simulation results under different signal-to-noise ratios show that using fractional Fourier transform can effectively realize target detection of a two-torpedo salvo and has strong anti-interference capabilities. In addition, two torpedoes can work in the same frequency band without frequency division, thus making the method feasible for use in two-torpedo salvo active homing.

torpedo; two-torpedo salvo; fractional Fourier transform; active homing; target detection

TJ630; TB566

A

2096-3920(2020)06-0677-08

10.11993/j.issn.2096-3920.2020.06.013

2020-07-31;

2020-09-28.

蒋 帅(1994-), 男, 在读硕士, 主要研究方向为鱼雷自导技术.

蒋帅, 樊书宏, 郝保安. 基于分数阶傅里叶变换的双雷齐射主动自导方法[J]. 水下无人系统学报, 2020, 28(6): 677-684.

(责任编辑: 杨力军)