一种滑动后向递推的EKF纯方位目标跟踪方法

郑 艺, 王明洲

一种滑动后向递推的EKF纯方位目标跟踪方法

郑 艺, 王明洲

(中国船舶重工集团公司 第705研究所, 陕西 西安, 710077)

由于只有一个观测点且只能获取目标方位信息, 被动的单站纯方位水下目标跟踪是定位跟踪领域的难点之一。在工程应用中有时存在观测时间短、数据量小的情况, 进一步加大了定位跟踪的难度。基于此, 文中研究了常规扩展卡尔曼滤波(EKF)原理, 分析了其在单站纯方位目标跟踪中状态估计变化的特点, 并通过公式推导进行了证明。针对短时观测、小数据量的特殊背景, 提出了一种滑动后向递推的EKF方法, 通过后向递推与正向递推的结合, 增加对数据的反复利用, 降低了估计误差。仿真试验结果证明, 在不同观测噪声、不同噪声协方差估计的情况下, 对于短时观测小数据量下的单站纯方位目标跟踪, 文中方法比常规EKF方法具有更低的误差。

水下目标跟踪; 后向递推; 扩展卡尔曼滤波; 纯方位; 短时观测

0 引言

水下单站纯方位的被动目标跟踪仅利用单个观测站在隐蔽的状态下对目标进行定位跟踪, 从而实现秘密的行动策划与目标打击, 是水下无源定位跟踪领域热点方法之一[1]。但由于只有一个观测站且只能获取目标方位信息, 水下单站纯方位目标跟踪也是最具挑战性的方法之一[2]。在实际应用场景中, 有时会存在目标运动速度快、观测时间短、观测数据量少的情况, 因此如何在较短的观测时间中实现快速收敛并降低估计误差, 是单站无源定位跟踪领域亟待解决的难点之一。

水下单观测站的纯方位目标定位利用测向交叉定位原理, 反映了一种非线性滤波问题[3]。针对这一类问题, 下列基于贝叶斯原理的递推类滤波方法得到广泛运用: 扩展卡尔曼滤波(extended Kalman filter, EKF)[4]通过对非线性方程进行1阶泰勒级数展开, 从而逼近真实的状态分布; 无迹卡尔曼滤波(unscented Kalman filter, UKF)[5]根据确定性采样方法, 通过无迹变换来获取目标的后验均值和协方差分布; 容积卡尔曼滤波(cubature Kalman filter, CKF)[6]通过三自由度球面-径向容积规则构建, 将非线性滤波看作非线性函数与高斯概率密度乘积的积分求解问题; 粒子滤波(particle filter, PF)[7]在每个时刻通过加权粒子集来估计目标的均值和标准协方差, 其缺点在于运算量大。近年来, 由这类算法衍生的一些算法也得到了学者们的关注, 例如: 通过一些特定的规则加入调整系数对算法进行改进的方法[8]; 基于QR分解的平方根类滤波算法[9-10]; 结合自适应算法对噪声统计进行估计的改进方法[11-12]; 基于粒子群优化方法的改进算法[13-14]。这些算法存在一个共同问题[15], 就是由于后续估计是通过前值递推所得, 前值的误差会对后续滤波结果造成持续影响。在短时观测、小数据量的情形下, 引入的误差难以快速消除, 状态估计前值对后值的影响效应更为明显。

文中根据分析EKF滤波中状态估计的变化特点, 提出一种基于滑动后向递推的EKF(sliding backward recursive-EKF, SBR-EKF)初值优化方法, 在不需要增加新的观测量的前提下, 利用现有的观测数据后向滤波, 通过前后双向的递推对目标状态进行估计。仿真结果表明, 该方法可以加快算法收敛速度, 降低估计误差, 得到更精确的目标状态估计值。

1 基于EKF的单站纯方位目标跟踪

1.1 观测模型

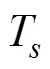
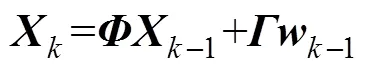
对于纯方位目标跟踪, 观测量是方位角, 观测方程为

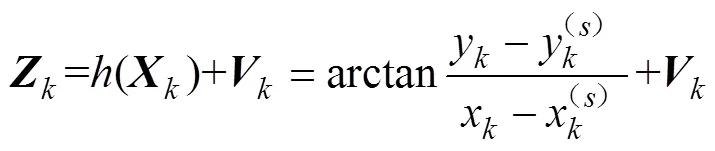
1.2 EKF步骤

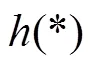
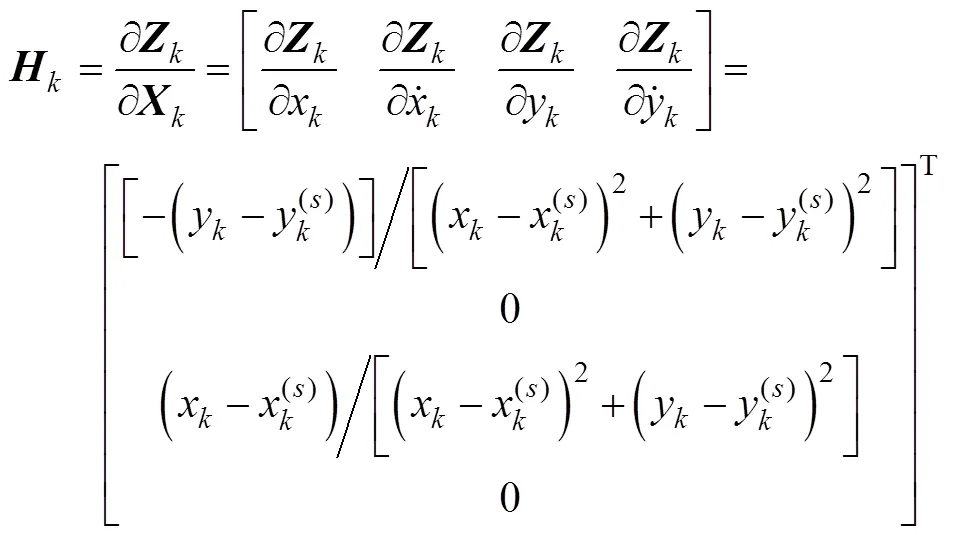
线性化后的观测方程为

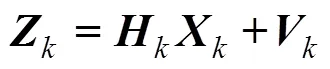
用状态方程(1)和线性化后观测方程(4)进行卡尔曼滤波, 可得到EKF的递推方程, 步骤和线性卡尔曼滤波相似, 为了减少线性化误差, 在计算状态预测和观测预测时, 仍然使用非线性函数。EKF具体步骤如下[4]。

1) 求解状态预测值

2) 求解状态协方差预测值

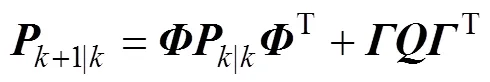
3) 求解卡尔曼增益矩阵

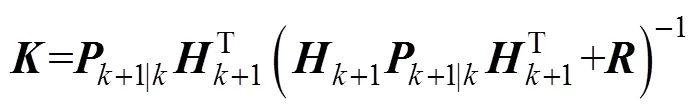
4) 状态更新

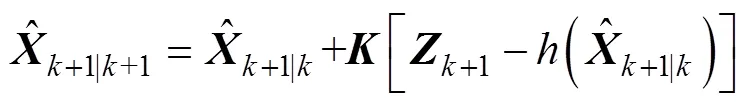
5) 协方差更新

通过式(5)~式(9), 可完成EKF一个计算周期, 整个计算过程就是通过各时刻获取的观测量反复循环计算, 从而获取各个时刻的目标状态估计。

2 状态估计变化方式

2.1 状态估计变化

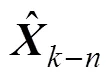
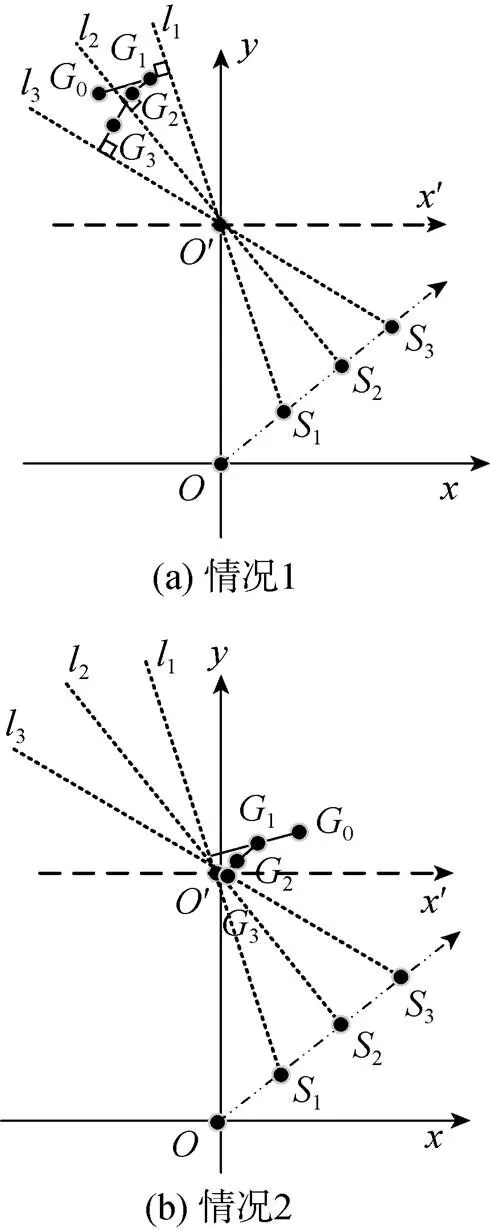
图1 目标状态估计位置变化

2.2 证明

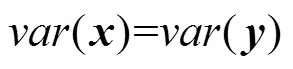
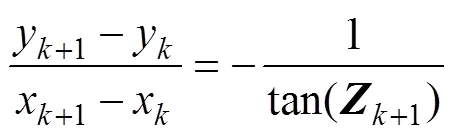
将式(8)按矩阵元素展开, 得

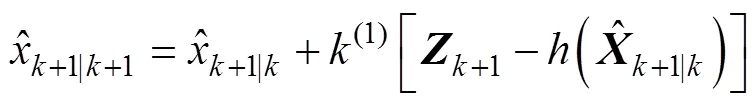
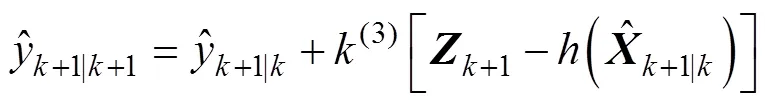
式中,(1)和(3)分别为卡尔曼增益矩阵中的第1、第3个元素。

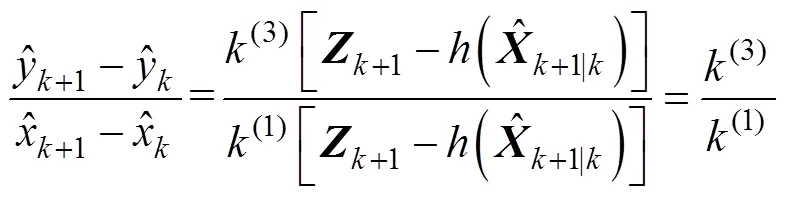
协方差矩阵初值

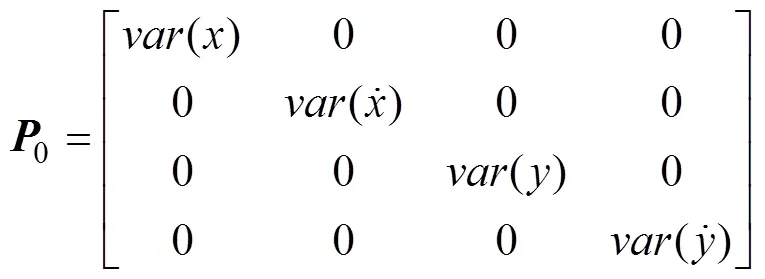
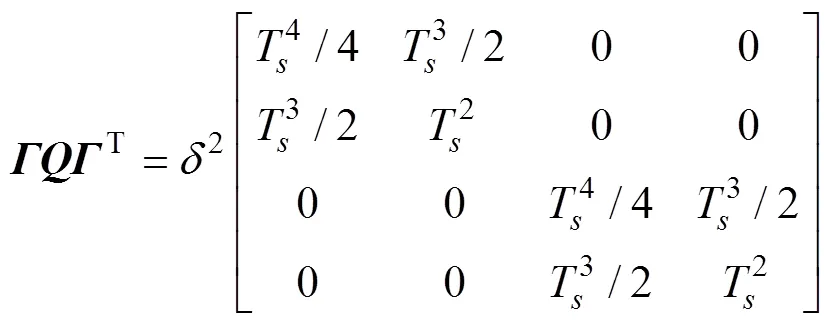
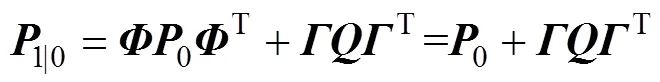
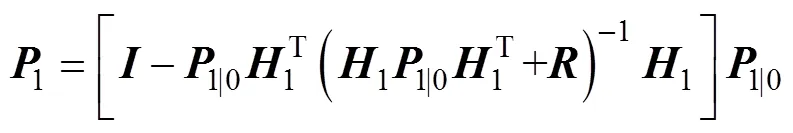
根据式(7)求卡尔曼增益矩阵

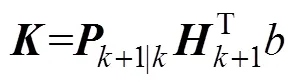
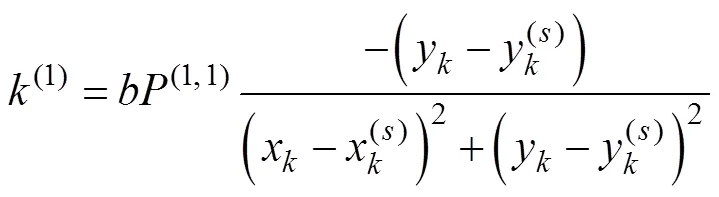
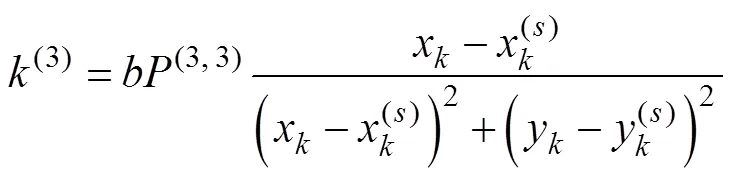
将式(20)除以式(19)得

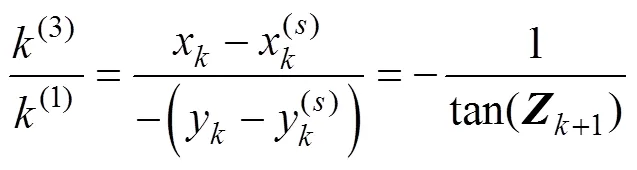
3 后向递推EKF

通过以上分析与证明可知, 由于目标状态并不随迭代直接向真实值靠近, 而是随着迭代向观测线方向靠近, 因此从初值选取开始, 状态估计前值的不同可能造成后续收敛情况不同, 常表现为初值对滤波的影响。当目标和观测站相对运动情况不同时, 状态估计结果可能不同。实际工程中, 由于无法预知估计值与真实值的位置关系, 估计值难以随递推逐渐收敛到真值附近。尤其在短时观测下, 观测数据量少且观测站机动不足, 难以保证估计的误差迅速缩小。文中提出的SBR- EKF可通过后向递推与正向递推结合, 增加对数据的反复利用, 从而降低滤波误差。

3.1 后向递推

将系统状态方程式(1)写成方程组形式

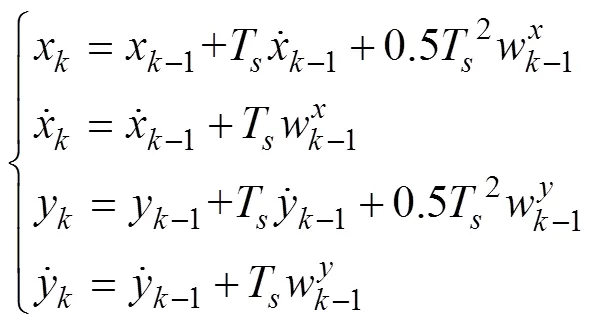
对于匀速直线运动目标, 其速度不变, 则有

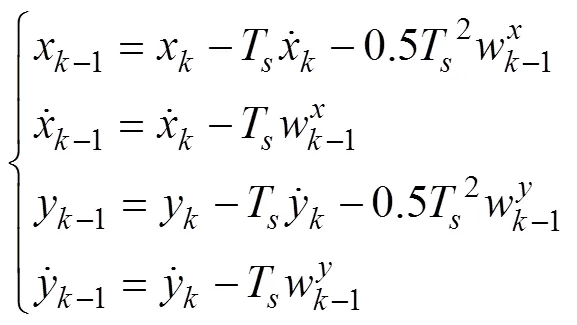
将式(23)写成矩阵的形式

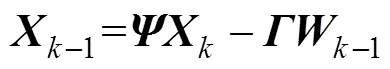
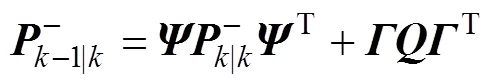
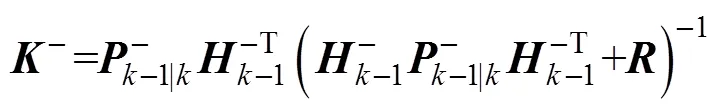
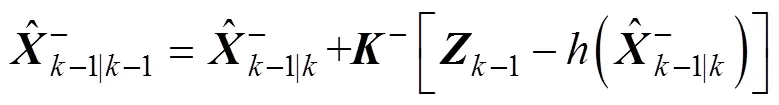
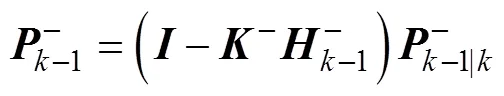
3.2 SBR-EKF

SBR-EKF方法通过在滑动窗内进行后向递推得到前值估计, 再根据新的前值估计重新进行目标状态估计。窗长为的SBR-EKF简要步骤如下:

图2 滑动后向递推示意图

Fig. 2 Diagram of sliding backward recursion

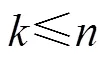
4 仿真与分析

为了验证所提出方法的有效性, 进行了以下仿真试验。文中的研究目的是解决快速运动目标短时观测下的纯方位被动跟踪问题, 比如高速运动平台的末程攻击情形, 特点为短时观测小数据量, 仿真参数设置以此为背景。进行100次蒙特卡洛试验, 用100次试验的均方根误差(root mean square error, RMSE)来衡量跟踪效果

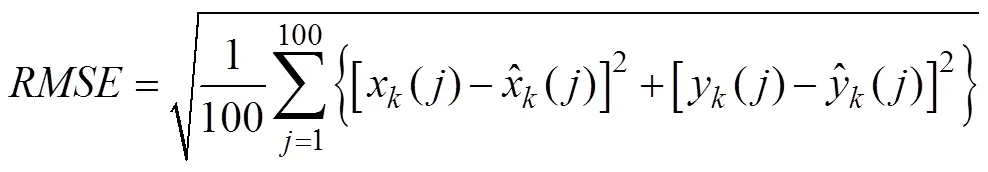
式中:为不同时刻对应采样点;为试验次数。RMSE可看作目标位置估计与目标真实位置之间的距离, 其值越小定位结果越准确。

设置目标初始位置为原点, 目标以45 kn的速度向东匀速直线行驶。观测站初始位置在目标东偏北35º方向, 以50 kn的速度向目标方向行驶, 以7º提前角追踪目标, 速度50 kn。观测站与目标的运动态势见图3。观测站对目标观测时间为6 s, 观测量为目标方位, 测向的时间间隔为0.1 s。

4.1 不同窗长比较

设置观测噪声(即不同测向误差)均值为0、协方差为2º, SBR-EKF的滑动窗长分别为1、5、10, 进行100次蒙特卡洛仿真。图4为EKF与不同窗长SBR-EKF的滤波RMSE比较, 可以看到, SBR-EKF相比于EKF有更低的RMSE, 且此种情况下窗长越长滤波效果越好。不同窗长SBR-EKF的单次滤波平均计算时间如表1所示, 并计算其相对于标准EKF的计算时间。结果显示与3.2节中计算量分析基本相符, 随取值增大, 计算时间增长。

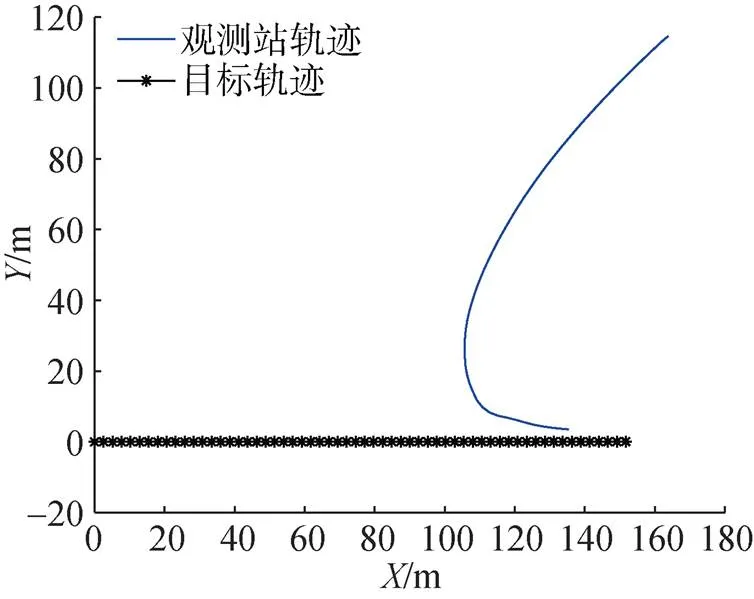
图3 观测站与目标的运动态势图

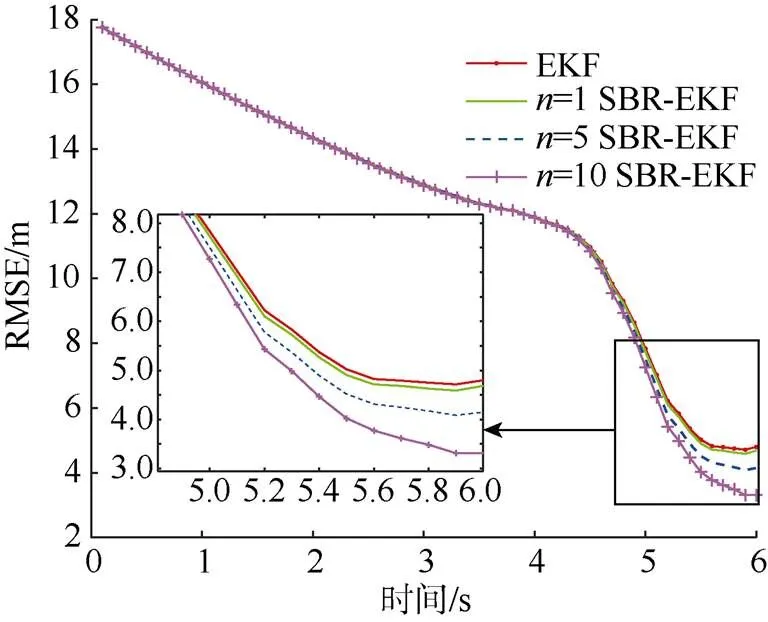
图4 SBR-EKF与EKF效果比较

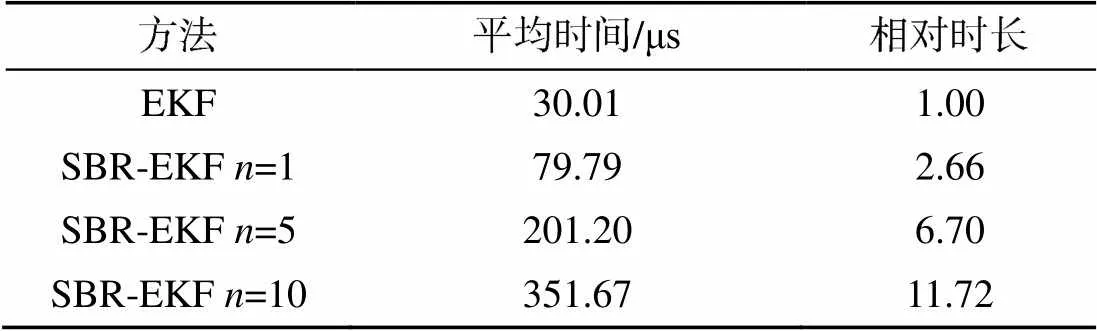
表1 单次滤波平均计算时间和相对时长

4.2 不同观测噪声比较

为了对比观测噪声下2种方法的性能, 在观测噪声协方差分别为1º~5º的情况下进行上述仿真试验。100次蒙特卡洛试验后, 统计仿真结果的平均RMSE如图5所示, 统计观测的最终时刻RMSE如图6所示。

从图中可以看到, 在不同的观测噪声下, 所提方法误差均小于常规EKF, 且对于最终误差的改善效果优于对于平均误差的改善效果。值得注意的是, 在观测噪声较大的情况下,取值越大, 平均误差和最终误差会更低; 而在观测噪声协方差阵较小(如1°)的情况下,=10的效果更差。这是由于观测噪声协方差较小的情况下, 过多的后向递推步数会造成对前值的过度估计, 使得滤波误差增大。因此在实际应用中, 根据观测噪声的情况和计算能力合理选择值是有必要的。

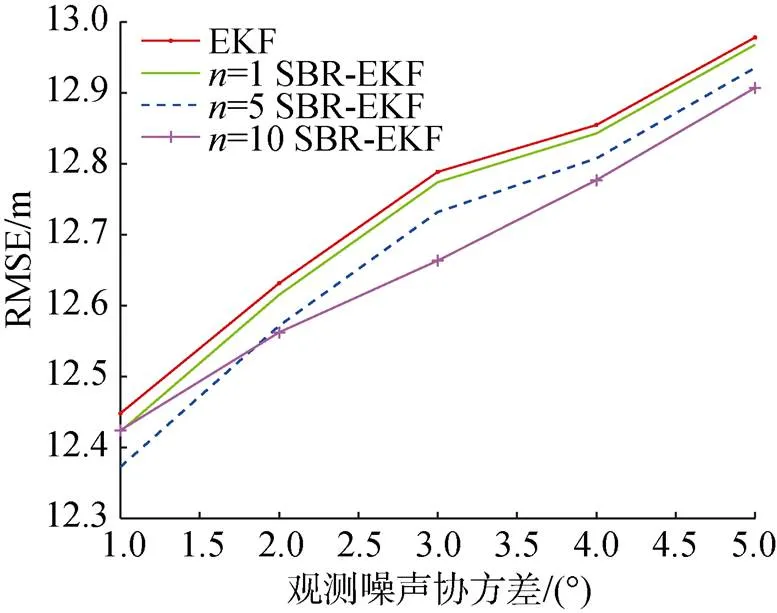
图5 不同测向精度下平均RMSE比较

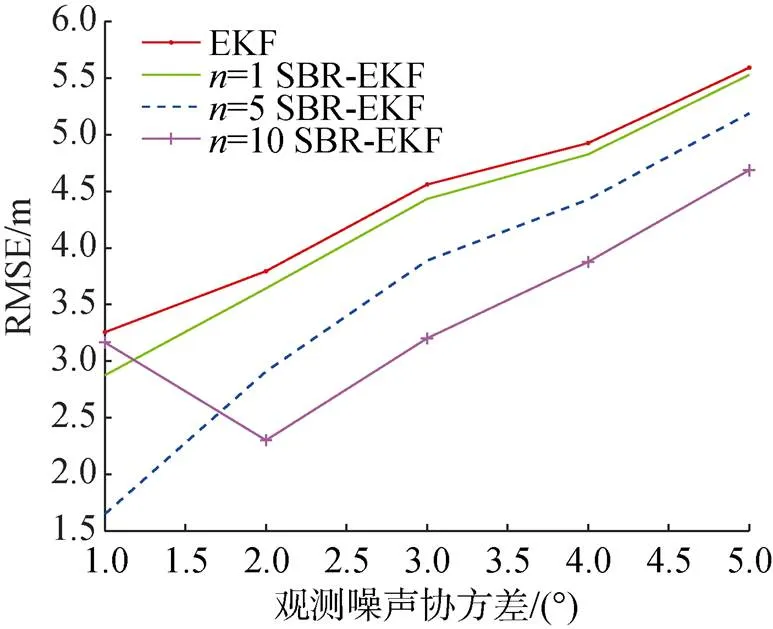
图6 不同测向精度下的最终RMSE比较

4.3 不同噪声协方差估计

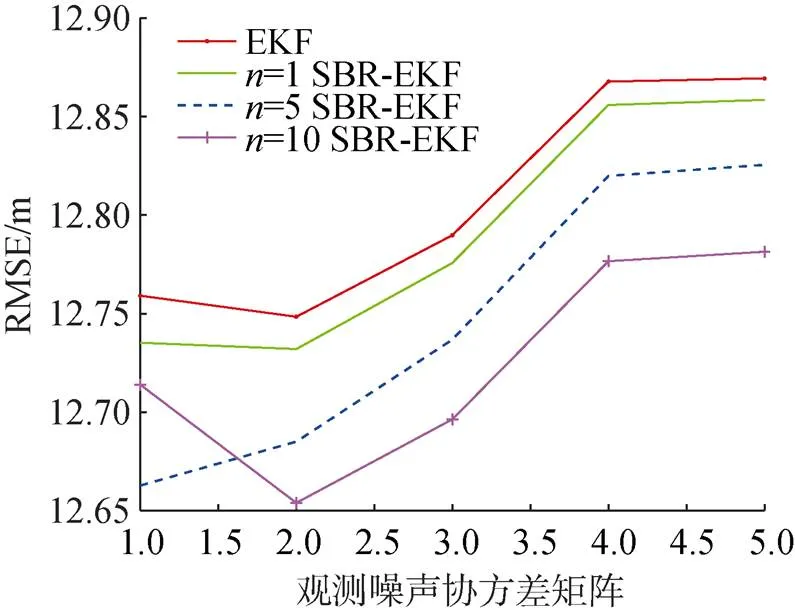
图7 不同观测噪声协方差估计

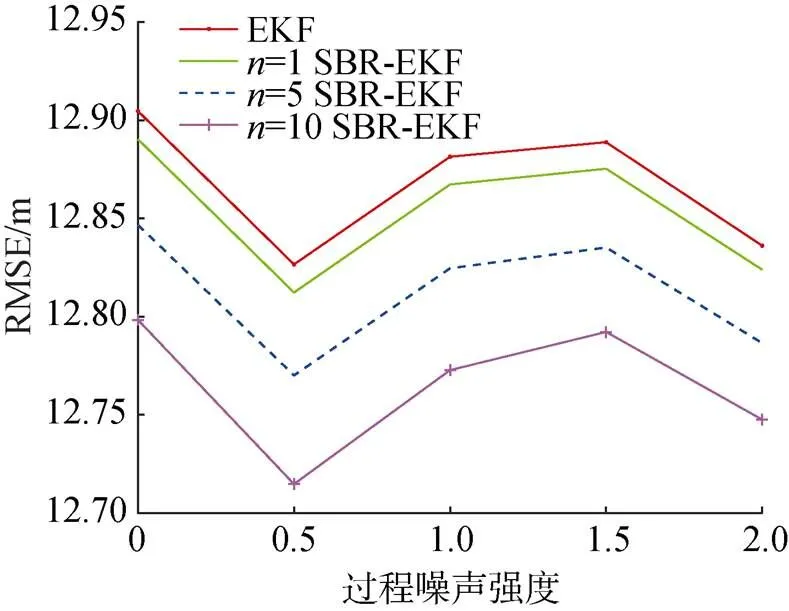
图8 不同过程噪声协方差估计

5 结束语

文中在短时观测小数据量的背景下, 提出了一种SBR-EKF的水下纯方位目标跟踪方法。该方法在常规EKF的基础上进行滑动后向递推, 通过观测数据的正反双向递推, 增加对数据的反复利用。仿真试验结果表明, 该方法相较于常规EKF有更好的性能, 可达到更低的估计误差, 表明了其较好的可行性和工程应用价值。该算法也适用于其他非线性滤波问题, 可为其他领域的应用提供新思路。后续的研究目标为探索更广泛的算法应用, 以及改善由于多次迭代导致的算法计算量增加问题。

[1] 刘忠, 周丰, 石章松, 等. 纯方位目标运动分析[M]. 北京: 国防工业出版社, 2009.

[2] Miller A B, Miller B M. Underwater Target Tracking Using Bearing-Only Measurements[J]. Journal of Comm- unications Technology and Electronics, 2018, 63(6): 643-649.

[3] 孙仲康, 郭福成, 冯道旺, 等. 单站无源定位跟踪技术[M]. 北京: 国防工业出版社, 2008.

[4] Shalom Y, Li X R, Thiagalingam K. Estimation with Applications to Tracking and Navigation[M]. New York: Wiley, 2001: 381-394.

[5] Julier S J, Uhlmann J K. Unscented Filtering and Nonlinear Estimation[J]. Proceedings of the IEEE, 2004, 92(3): 401-422.

[6] Arasaratnam I, Haykin S. Cubature Kalman Filters[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1254-1269.

[7] Gordon N J, Salmond D J, Smith A F M. Novel Approach to Nonlinear/non-Gaussian Bayesian State Estimate[J]. IEEE Proceeding of Radar, Sonar and Navigation, 1993, 140(2): 107-113.

[8] Zhao J. Dynamic State Estimation with Model Uncertainties Using∞Extended Kalman Filter[J]. IEEE Transactions on Power Systems, 2018, 33(1): 1099-1100.

[9] Li X, Zhao C, Yu J, et al. Underwater Bearing-only and Bearing-Doppler Target Tracking Based on Square Root Unscented Kalman Filter[J]. Entropy, 2019, 21(8): 740.

[10] Lim J, Shin M, Hwang W. Variants of Extended Kalman Filtering Approaches for Bayesian Tracking[J]. Internat- ional Journal of Robust and Nonlinear Control, 2016, 27(2): 319-346.

[11] He R, Chen S X, Wu H, et al. Adaptive Covariance Feedback Cubature Kalman Filtering for Continuous-Discrete Bearings-Only Tracking System[J]. IEEE Access, 2019, 7: 2686-2694.

[12] Zhou W, Liu L. Adaptive Cubature Kalman Filter Based on the Expectation-Maximization Algorithm[J]. IEEE Access, 2019, 7: 158198-158206.

[13] Zhao Y, Wang T, Qin W, et al. Improved Rao-Blackwell- ised Particle Filter Based on Randomly Weighted Particle Swarm Optimization[J]. Computers and Electrical Engineering, 2018, 71: 477-484.

[14] Liu H, He B, Feng C, et al. Navigation Algorithm Based on PSO-BP UKF of Autonomous Underwater Vehicle[C]// IEEE Underwater Technology(UT). Kaohsiung, Taiwan: IEEE, 2019.

[15] Konatowski S, Kaniewski P, Matuszewski J. Comparison of Estimation Accuracy of EKF, UKF and PF Filters[J]. Annual of navigation, 2016, 23(1): 69-87.

Sliding Backward Recursive EKF Bearings-Only Target Tracking Method

ZHENG Yi, WANG Ming-zhou

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi’an 710077, China)

In the field of target location and tracking, when only one observer is present and only the bearings of the target can be obtained, passive bearings-only underwater target tracking by a single observer is difficult. In engineering applications, the time of observation is short and the amount of data is sometimes small, which makes target location and tracking more difficult. In this study, the principle of a conventional extended Kalman filter(EKF) is studied and the characteristics of state estimation changes in bearings-only target tracking by a single observer are analyzed and proved by formula derivation. Considering the special background of short-term observation and the existence of a small amount of data, this study proposes a sliding backward recursive EKF method. Through a combination of backward and forward recursion, the data are reused and estimation errors are reduced. In a simulation of different observation noises and noise covariance estimates, results show that the proposed method generates lower errors than the conventional EKF for bearings-only target tracking by a single observer using a small amount of short-term observation data.

underwater target tracking; backward recursion; extended Kalman filter(EKF); bearings-only; short-term observation

TJ630.34; U664.82

A

2096-3920(2020)06-0663-07

10.11993/j.issn.2096-3920.2020.06.011

2020-07-14;

2020-09-27.

郑 艺(1992-), 女, 在读博士, 主要研究方向为水下目标跟踪定位.

郑艺, 王明洲. 一种滑动后向递推的EKF纯方位目标跟踪方法[J]. 水下无人系统学报, 2020, 28(6): 663-669.

(责任编辑: 杨力军)