邻近建筑物的滨海土岩组合基坑支护结构变形分析*

胡瑞庚 刘红军②③ 王兆耀 郗玉婷

(①中国海洋大学环境科学与工程学院， 青岛 266100， 中国)(②山东省海洋环境地质工程重点实验室， 青岛 266100， 中国)(③海洋环境与生态教育部重点实验室， 青岛 266100， 中国)(④青岛理工大学土木工程学院， 青岛 266033， 中国)(⑤青建集团股份公司， 青岛 266100， 中国)

0 引 言

现代化城市建设往往采用“见缝插针”的方式，特别对于老城的拆建区，拟建建筑可能位于四周已建建筑群中，这就要求拟建建筑在建设过程中尽可能减少对周围环境的扰动，而深基坑工程涉及对土体的开挖卸载，容易对周围环境造成扰动。

青岛为海滨丘陵城市，具有典型的“土岩组合”地层结构，以土岩组合界面为限，上、下体现为力学性质几乎完全不同的两种材料，需考虑支护结构在土、岩材料中的受力性能差异进行设计(Ma et al.，2008; 张勇等， 2009; 陈竑然等， 2019)。

目前国内外学者主要采用数值模拟与现场实测的方法对土岩基坑支护结构变形规律进行研究，并取得了一定的研究成果。刘红军等(2011， 2012)分别采用双排桩加锚杆、双排吊脚桩、吊脚桩加锚索等方式对土岩基坑进行支护，取得了良好效果，开挖引起的土体变形得到了有效控制。徐锦斌等(2014)采用PLAXIS有限元软件，研究了土岩基坑开挖过程中支护结构变形和受力规律。张传军等(2016)采用吊脚桩联合锚索对土岩基坑进行支护，结果发现：当上覆土层较薄时，支护结构的变形主要集中在上覆土层中。祝文化等(2012)研究了不同荷载组合状态下地铁车站土岩基坑变形规律。白晓宇等(2018)对土岩基坑的桩锚联合内支撑支护结构进行变形分析，结果表明基坑水平位移的最大值出现在上部软弱土层。周贺(2011)、吴燕开等(2013)、翟桂林(2013)、郑学东(2017)分别对土岩基坑开挖引起的周围土体变形规律进行了研究，得到了周围土体变形模式。彭晶(2014)、闫楠等(2015)探讨了邻近超载对土岩基坑变形的影响规律。

基坑开挖的不同阶段、不同部位的应力变化过程不同，即土体卸荷的应力路径不同，要准确描述开挖引起的变形问题，需要能反映土体加卸载刚度差异、土体剪切硬化和压缩硬化的高级本构模型。 Benz(2006)、Yin (2010)、Ardakani et al.(2014)、Shao et al.(2015)采用能同时考虑土的剪切硬化和压缩硬化的硬化土模型(Hardening Soil Model， HS)对基坑变形问题进行了数值计算和验证。Xu et al.(2010)对比了不同本构模型在基坑工程分析中的适用性，表明硬化类本构模型适用于敏感环境下基坑开挖变形分析。王春波等(2014)推导了HS模型有限差分格式，并用于基坑分析，得出HS模型不仅能反映土体的剪胀性和压硬性，还能反映不同区域土体的应力路径。管飞(2010)采用小应变硬化土模型(HSS)计算了软土基坑开挖对周围环境的影响，验证了HSS模型在软土基坑工程中的适用性。王卫东等(2013)获得了HSS模型的参数，为进一步应用HSS模型提供了借鉴作用。

由以上学者们的研究成果可以看出：不管选用何种支护形式，土岩基坑支护结构的变形主要集中在上覆土层中； 已有研究采用数值模拟与现场监测结合的方法得到了支护结构的变形规律，但对于邻近建筑物等敏感环境下土岩基坑支护结构的变形规律研究较少，而且对土岩基坑中的土体多选用理想弹塑性模型(如莫尔-库仑模型)，关于敏感环境下土岩基坑开挖引起的变形分析问题，对土体本构模型适用性的研究较少见。基于此，本文基于PLAXIS有限元软件，以邻近建筑物的滨海土岩组合基坑工程为例，选用微型钢管桩-锚杆-土钉支护方式，探讨不同土体本构模型对基坑开挖引起支护结构变形问题的适用性，在此基础上，研究本案例支护形式中两个关键因素(锚杆预应力系数、微型钢管桩抗弯刚度)对支护结构变形的影响规律。

1 工程概况及设计支护方案

拟建场区位于青岛市辽阳路以南，福州路以西，共包括1幢18层建筑， 1幢3层建筑，两栋楼下均带有两层地下室。

拟建场区整体地形自西南向东北缓倾，钻孔地面标高：56.39～63.75 m。场区属剥蚀堆积缓坡地貌，场区揭露的第四系厚度约4.0～10.9 m，钻探结果表明，场区第四系结构简单，层序清晰，由全新统粉质黏土层、上更新统洪冲积层组成。场区基岩主要为粗粒花岗岩，局部受微构造影响穿插构造破碎带。

本文选取邻近建筑物的基坑一侧作为计算单元。计算单元上覆土层只有粉质黏土，厚度约4.3～5.9 m，土层下面是花岗岩强风化带，基坑开挖约13.08～15.65 m，地下水位深度约6.3～6.8 m，分布于花岗岩强风化带中。

对基坑地下水控制采用管井降水方案，井壁管孔径φ650 mm，滤水管内径φ400 mm，深度15.2～23.0 m，间距7.5～8.7 m。本单元距基坑开挖边线0.8 m处有地下管线，距2.7 m处有1幢3层建筑物，由于基坑邻近建筑物和地下管线，对变形控制要求较高，开挖前采用微型钢管桩超前支护，在开挖过程中，微型桩可以承担部分侧面土压力从而减小基坑边坡的变形量(施有志等， 2018; 赵梦怡等， 2018; 李楠等， 2019)。在基坑开挖过程中，分层间隔打设土钉、预应力锚杆。

采用弹性支点法对支护方案进行设计计算，基坑支护结构安全等级取二级(建筑基坑支护技术规程(JGJ120-2012))，计算得到的支护设计方案见图1。

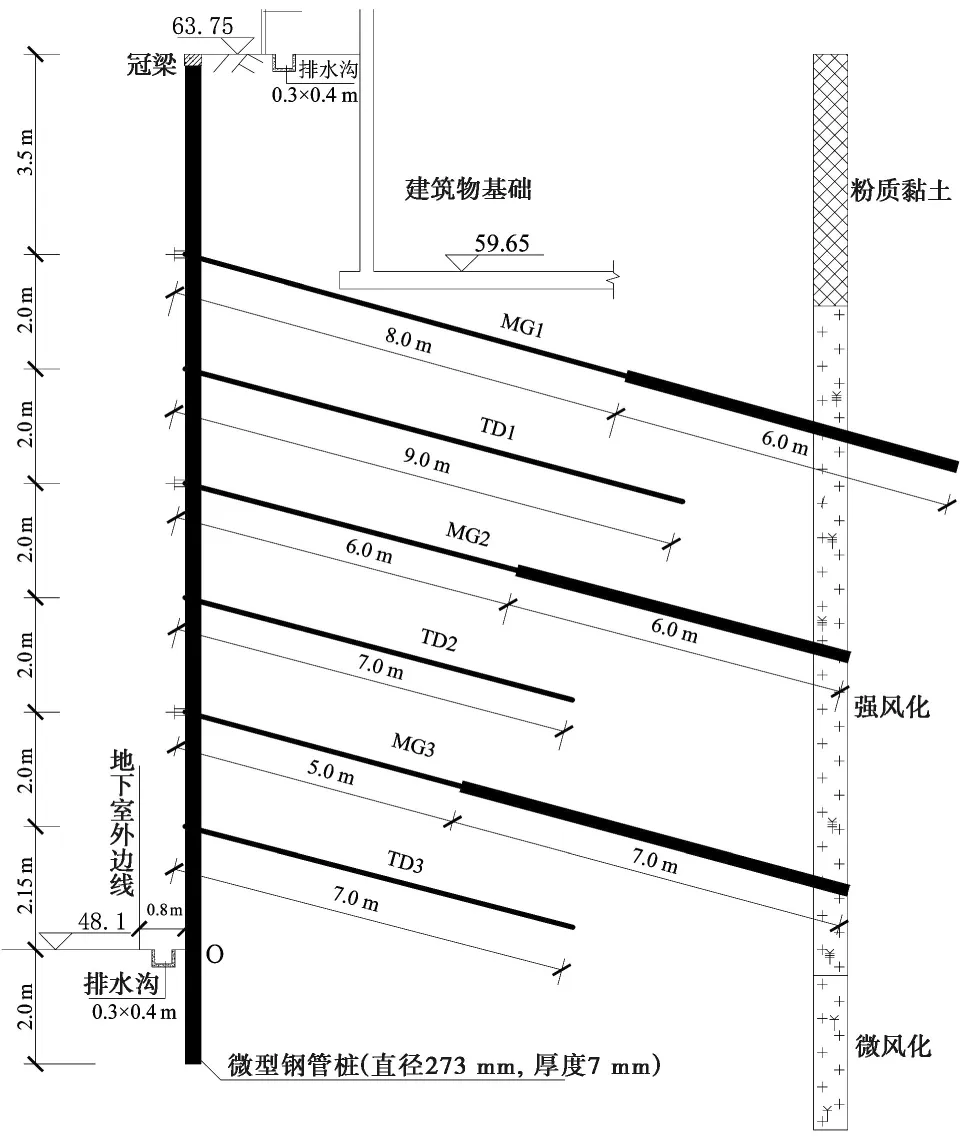
图1 支护方案设计图Fig.1 Project design of supporting structuresTD为土钉； MG为锚杆

2 有限元模型建立

基于上文的方案设计，采用PLAXIS有限元软件建立基坑有限元模型。基坑开挖影响分析采用平面应变模型，计算单元中基坑开挖深度15.65 m，为减小边界条件的影响，模型深度取1.8倍的基坑开挖深度，即27 m，长度为30 m。为提高计算精度，模型采用15节点单元。邻近基坑的建筑物采用框架结构进行模拟，内部填充线弹性材料，建筑物产生的超载施加于基础埋深处。

2.1 土体本构模型参数的选取

为获得适用于土岩组合基坑问题分析的土体本构模型，土层分别选取莫尔-库仑模型(MC)、修正剑桥模型(MCC)、硬化土模型(HS)、小应变硬化土模型(HSS)，岩层选取莫尔-库仑模型(MC)，各本构模型的参数获取如下所述：

2.1.1 莫尔-库仑模型(MC)

本文选取计算案例的勘察报告给出了土层泊松比ν、黏聚力c、内摩擦角φ的值，弹性模量E根据高大钊等(2006)给出的弹性模量与压缩模量之间经验公式而获得，根据Bolton(1986)的研究，对于黏性土ψ一般取为0。采用MC模型时土层的参数取值见表1。

表1 土(岩)层的参数取值表(MC模型)Table1 Parameter values of soils(MC model)

2.1.2 修正剑桥模型(MCC)

修正剑桥模型需要破坏常数M、回弹参数κ、各向等压固结参数λ、初始孔隙比einit和卸载泊松比νur5个参数，其中M、einit分别根据式(1)、式(2)确定(赵成刚， 2012)，κ、λ、νur根据陈建峰等(2003)、陈源(2014)推荐的方法获得，采用MCC模型时土层的参数取值见表2。

表2 土层的参数取值表(MCC模型)Table2 Parameter values of soils(MCC model)

(1)

(2)

式中：φ为土体内摩擦角(°)；Gs土体比重；ω为土体含水率；ρω为水的密度(g·cm-3);ρ为土体密度(g·cm-3)

2.1.3 硬化土模型(HS)

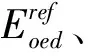
表3 土层的参数取值表(HS模型)Table3 Parameter values of soils(HS model)

图2 三轴固结排水试验的偏应力-应变曲线Fig.2 The curve of partial stress-strain under triaxial consolidation drainage tests

(3)

2.1.4 小应变硬化土模型(HSS)

HSS模型的输入参数有13个，其中11个参数与HS模型相同(表3)，除此之外，HSS模型增加了考虑土体小应变的2个参数：小应变范围初始剪切模量G0和剪切应变水平γ0.7(割线模量G0减小到70%G0时的应变水平)。

G0、γ0.7采用王卫东等(2013)推荐的方法获得，通过计算，粉质黏土层这2个参数取值分别为：G0=127.5 MPa，γ0.7=6.13×10-7。

2.2 结构单元参数

采用板单元模拟微型钢管桩，采用点对点锚杆单元模拟锚杆的自由段，采用土工格栅单元模拟锚杆的锚固段和土钉。

2.2.1 板单元

微型钢管桩采用板单元模拟，微型钢管桩的弹性模量E=220 GPa，注浆体弹性模量E=25.5 GPa，桩直径273 mm，桩的水平间距为1.5 m。

根据PLAXIS模型手册(Brinkgreve et al.，2010)计算得到板单元的输入参数为：等效厚度d=0.122 62 m，抗压刚度EA=3.126×106ikN，抗弯刚度EI=3917.81 kN·m2。

2.2.2 土工格栅单元

土钉采用土工格栅单元模拟，根据PLAXIS模型手册(Brinkgreve et al.，2010)计算得到的各层土钉的输入参数见表4。

表4 土工格栅单元输入参数取值表Table4 Parameter values of geogrid elements

2.2.3 点对点锚杆单元

锚杆的锚固段采用点对点锚杆单元模拟，锚杆的自由段采用土工格栅单元模拟，根据PLAXIS模型手册(Brinkgreve et al.，2010)计算得到的锚杆单元输入参数见表5。

表5 点对点锚杆单元输入参数取值表Table5 Parameter values of point to point anchor elements

2.3 模拟工况

基坑的开挖是分时、分段、分步进行的，同时在基坑开挖过程中会穿插打设预应力锚杆和土钉进行支护，结合本案例基坑开挖、支护的顺序，将模拟的基坑开挖有限元模型建立5个工况，分别为：

工况1：施加建筑物超载，并将产生的位移清零；

工况2：打设微型钢管桩； 开挖4.4 m，打设MG1；

工况3：开挖3.5 m，打设TD1、MG2；

工况4：开挖3.5 m，打设TD2；

工况5：开挖4.25 m，打设MG3、TD3；

3 计算结果分析

3.1 不同本构模型结果对比分析

3.1.1 基坑开挖引起的竖向位移

不同本构模型计算得到的竖向位移云图如图3所示。

从图3可以看出，MC模型中基坑开挖引起的周围环境沉降模式与其他3个模型不同，MC模型中基坑开挖引起的竖向位移最大值为3.06 mm，发生在第一道锚杆的锚固端附近，MCC、HS与HSS模型中基坑开挖引起的周围环境沉降模式相似，竖向位移最大值均发生在邻近建筑物基底处，其中MCC模型中竖向位移最大值为180.36 mm， HS与HSS模型中的最大竖向位移相近，分别为35.96 mm、35.29 mm，约为MCC模型计算值的19.94%、19.57%。

图3 不同本构模型下竖向位移云图Fig.3 Vertical displacement nephograms under different constitutive modelsa.MC模型； b.MCC模型； c.HS模型； d.HSS模型

为量化比较不同本构模型情况下基坑周围土层沉降值与实测值的差异，在程序中提取从基坑开挖边至距坑边22.5 m范围内地表的沉降值，并与现场实测值进行比较(图4)。

图4 不同本构模型下基坑开挖引起的地表沉降曲线Fig.4 The curves of vertical displacements induced by excavation under different constitutive models

如图4所示，MC模型中基坑周围地表沉降几乎为零，与实测值相差较大，不能反映在邻近建筑物超载情况下，基坑开挖卸载引起的周围环境的沉降变化规律，原因是MC模型作为理想弹塑性模型，适用于极限平衡条件下土体强度的分析问题，而不适于描述土体的变形和应力-应变过程。

MCC模型中建筑物基底沉降值约为180.21 mm，约为实测值的3.11倍，说明MCC模型过分反映了基坑开挖卸载引起的周围环境沉降值，这是由于MCC模型虽然能反映土体的压硬性，而基坑开挖引起周围土层的侧向压力减小，属于卸载过程，MCC模型不能反映土体软化特性，故其描述应力路径变化引起的土体竖向变形效果较差。

HS、HSS模型中基坑开挖引起的地表沉降模式相似，与实测值的变化趋势一致，由于HS、HSS模型不仅能同时反映土体的剪切硬化和压缩硬化，而且能反映加、卸载刚度的差异，能较好的反映在邻近建筑物超载情况下，基坑开挖卸载引起的周围环境的沉降变化规律。

在HSS模型中，分别距基坑开挖边L处提取地表沉降值，得到不同计算点沉降值随开挖工况的变化曲线(图5)：

图5 地表沉降计算值随开挖工况的变化曲线Fig.5 The curves of vertical displacements under different excavation conditionsa.邻近建筑物靠近基坑一侧； b.邻近建筑物远离基坑一侧

由图5可以看出，分别在距建筑物距离L=2.58 m、L=10.59 m处，基坑开挖引起的沉降值最大，基坑开挖对邻近建筑物靠近基坑一侧计算点的沉降值影响显著。相比于其他工况，工况2(开挖4.4 m，打设MG1)引起的计算点沉降值增加明显，说明土层沉降对初始卸载的反应最为敏感。随着基坑开挖的进行，计算点的沉降值变化幅度减缓，在进行至工况5(基坑开挖至基底)，计算点的沉降值趋于稳定。

3.1.2 基坑开挖引起的水平位移

为比较不同本构模型情况下计算的水平位移值与实测值的差异，提取不同深度处桩身水平位移值(图6)。

图6 不同本构模型下桩身水平位移变化曲线Fig.6 The curves of horizontal displacement of pile under different constitutive models

如图6所示，不同本构模型计算得到的桩身水平位移最大值均发生在地表处，方向均指向坑内，由于锚杆预应力的约束作用，桩身在第一道锚杆(MG1)处，均发生指向坑外的位移； 在花岗岩强风化层中，由于花岗岩均采用的MC模型，计算得到的水平位移值基本相同，桩身水平位移在锚杆约束处为零，在两层锚杆之间发生指向坑内的水平位移。

在粉质黏土层中，MC模型中地表最大水平位移为10.73 mm，约为实测值的59.72%，两者相差较大，说明MC模型不能准确计算出基坑开挖引起的桩身水平位移，而且随着基坑开挖深度的增加，MC模型计算的桩身水平位移值与实测值的误差逐渐增大。

MCC模型中地表最大水平位移为19.86 mm，约为实测值的1.11倍，在第一道锚杆处，水平位移为6.18 mm，约为实测值的50.22%，说明MCC模型能准确的计算出地表处的最大水平位移值，但随着基坑开挖深度的增加，MCC模型计算的桩身水平位移值与实测值的误差逐渐增大。

相比于HS模型，HSS模型中桩身水平位移值与实测值更为接近，HSS模型计算的地表最大水平位移为15.97 mm，约为实测值的88.87%，在第一道锚杆处，水平位移为10.31 mm，约为实测值的83.75%，说明HSS模型能较准确的描述邻近建筑物超载、基坑开挖卸载引起的桩身水平位移的变化规律，这是由于基坑工程中的土体在工作荷载下一般仍处于小应变状态(赖勇等， 2005; Teo et al.，2012)，HSS模型考虑了小应变范围内土体的剪切刚度的非线性，并考虑了邻近建筑物超载、基坑开挖卸载引起的加荷和卸荷过程中土体的刚度差异，较准确地描述了该过程土体的剪切硬化和压缩硬化。

综合比较竖向位移图、水平位移图可知，HSS模型较适用于描述邻近建筑物土岩组合基坑的变形规律。

3.2 基于HSS本构模型的结果分析

3.2.1 锚杆预应力系数对土层水平位移的影响

粉质黏土选取HSS模型，锚杆锁定预应力分别取锚杆轴向拉力设计值(N)的0.5倍、0.75倍、0.85倍、1.0倍、1.1倍，即预应力系数η分别为0.5、0.75、0.85、1.0、1.1，具体参数取值见表6。

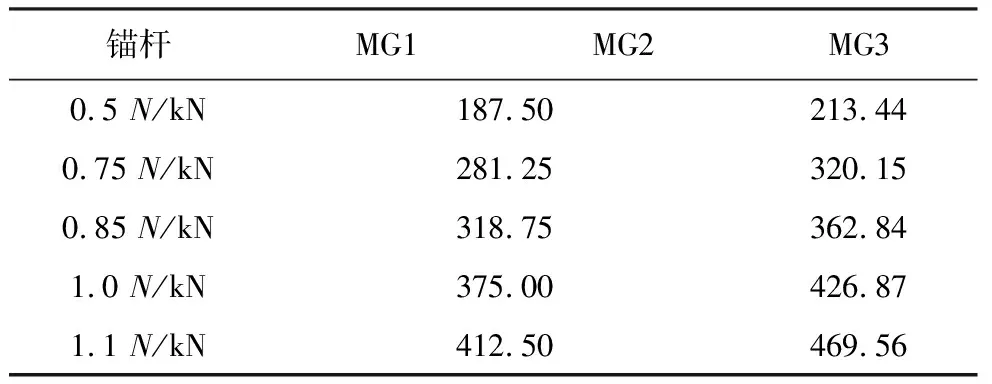
表6 锚杆张拉力取值表Table6 Parameter values of anchor pre-stress

为比较不同深度处锚杆预应力系数η对水平位移值的影响规律，提取不同预应力系数下桩身的水平位移值(图7)。

图7 不同预应力系数η下桩身水平位移曲线Fig.7 The curves of horizontal displacement of pile under different prestress coefficients η

由图7可以看出，不同预应力系数η下，桩身水平位移最大值均出现在地表处，方向均指向坑内； 在第一道锚杆(MG1)处，当η=0.5时，桩身发生指向坑内的水平位移，当η>0.75时，桩身均发生指向坑外的水平位移，且水平位移的发展与η呈正相关，这是由于锚头处约束力随着η的增加而增大，锚头处约束力的增加对该处水平位移的控制发挥有利作用，同时，地表水平位移随着η的增加而增大，这对地表水平位移的控制是不利的，因此，第一道锚杆的预应力系数η对锚杆和地表处水平位移的控制具有显著影响。

在花岗岩风化层，随开挖深度的增加，相邻两道锚杆之间桩身水平位移以锚杆处为支点，呈“鼓肚状”分布，方向指向坑内，最大值出现在相邻两道锚杆中点处。相邻两道锚杆支点处桩身水平位移、桩身最大水平位移随η的增加而减小，但当η>0.75时，η对桩身水平位移的影响效果减弱。

3.2.2 微型钢管桩抗弯刚度对土层水平位移的影响

粉质黏土选取HSS模型，钢管桩注浆体的弹性模量E为25.5GPa，分别设置钢管桩的直径D为273 mm、325 mm、377 mm，计算钢管桩的轴向刚度EA、抗弯刚度EI，具体参数取值见表7。

表7 微型钢管桩刚度输入参数取值表Table7 Parameter values of rigidity of micro steel pipe pile

取锚杆的预应力系数η=0.75，钢管桩的直径D取273 mm、325 mm、377 mm时计算得到的抗弯刚度分别为a、b、c，计算得到不同抗弯刚度下桩身水平位移变化曲线(图8)。

图8 不同抗弯刚度下桩身水平位移曲线Fig.8 The curves of horizontal displacement of pile under different flexural rigidity

由图8可以看出，在地表处，桩身水平位移方向均指向坑内，抗弯刚度对桩身水平位移的影响主要发生在自地表向第一锚杆深度范围内，当抗弯刚度由a增加至c时，地表水平位移减小了6.50 mm，第一道锚杆处水平位移减小了1.74 mm，说明增加钢管桩的抗弯刚度对地表处的水平位移控制效果更明显。

由上文分析可知，不同锚杆预应力系数η、不同微型钢管桩抗弯刚度情况下桩身水平位移最大值均出现在地表处，同时，地表水平位移与第一道锚杆预应力系数η的变化呈正相关。因此，为分析锚杆预应力系数η和钢管桩抗弯刚度的联合作用对桩身水平位移的影响规律，可选取地表处和第一道锚杆处桩身水平位移为控制因素，得到地表处和第一道锚杆处桩身水平位移变化曲线(图9)。

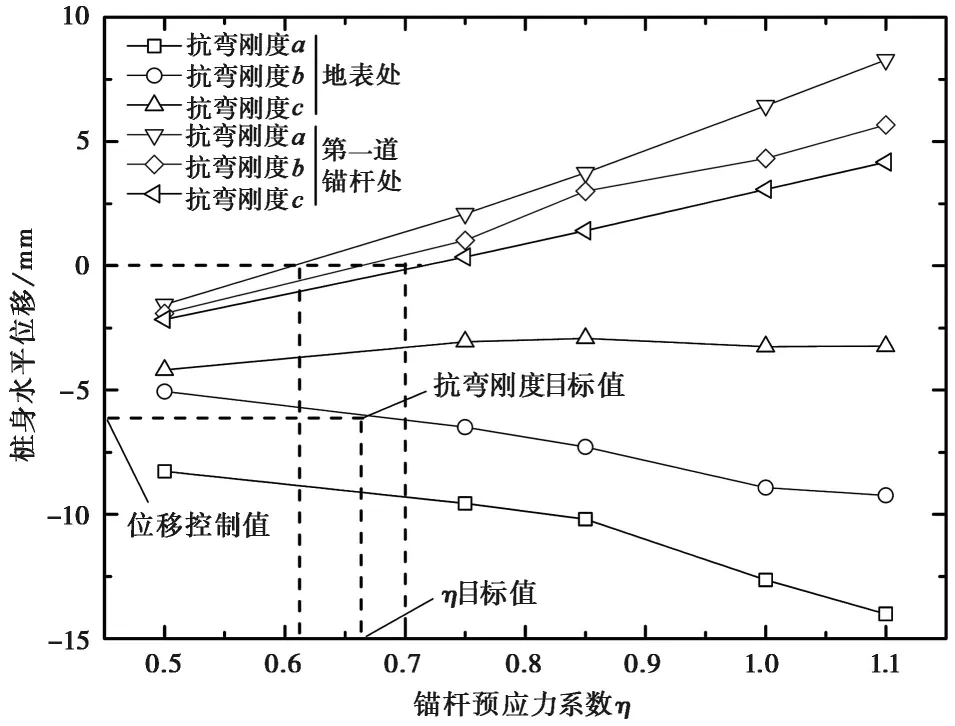
图9 地表处和第一道锚杆处桩身水平位移变化曲线Fig.9 The curves of horizontal displacement of pile at ground surface and the first anchor图中负值位移方向指向坑内

由图8、图9可以看出，相邻两道锚杆之间桩身水平位移以锚杆处为支点，呈“鼓肚状”分布，且支点处桩身水平位移随η的增加而减小，即当η较小时，可认为锚杆在支点处的约束力不够，桩身仍会发生指向坑内的位移，此时的η不能很好地控制桩身水平位移。因此，取第一道锚杆处桩身水平位移为零，可以确定η的取值范围。

如图9所示，当η的取值范围确定后，根据基坑周围环境对水平变形的要求，选取合适的η目标值，最后根据η目标值确定钢管桩抗弯刚度，从而使锚杆-微型钢管桩形成变形协调的支护体系。

4 结 论

(1)MC模型不能反映在邻近建筑物超载情况下，基坑开挖卸载引起的周围环境的沉降变化规律，MCC模型过分反映了基坑开挖卸载引起的周围环境沉降值，HS、HSS模型中基坑开挖引起的地表沉降模式相似，与实测值的变化趋势一致。

(2)随着基坑开挖深度的增加，MC、MCC模型计算的桩身水平位移值与实测值的误差逐渐增大，HSS模型能较准确地描述邻近建筑物超载、基坑开挖卸载引起的桩身水平位移的变化规律。

(3)不同锚杆预应力系数η和微型钢管桩抗弯刚度情况下桩身水平位移最大值均出现在地表处，第一道锚杆的预应力系数η对锚杆和地表处水平位移的控制具有显著影响。

(4)取第一道锚杆处桩身水平位移为零，可以确定η的取值范围，根据基坑周围环境对水平变形的要求，选取合适的η目标值，最后根据η目标值确定钢管桩抗弯刚度，从而使锚杆-微型钢管桩形成变形协调的支护体系。