基于统计理论的青海河南县地区5种草本植物根系力学特性研究*
付江涛 李晓康 刘昌义 余冬梅 鲁秋菊 孟宏睿 胡夏嵩
(①陕西理工大学土木工程与建筑学院, 汉中 723000, 中国)(②陕西理工大学数学与计算机学院, 汉中 723000, 中国)(③青海大学地质工程系, 西宁 810016, 中国)(④中国科学院青海盐湖研究所, 西宁 810008, 中国)
0 引 言
近年来随着人们对生态环境保护认识的逐渐提高,利用植物对边坡开展防护的应用愈来愈广泛(Reubens et al.,2011; Caviezel et al.,2014; 肖涛, 2019; 李姜瑶等, 2020; 刘亚斌等, 2020)。植被护坡技术的应用始于16世纪,但其理论发展则始于20世纪60年代(付江涛等, 2014; 肖涛等, 2019)。Gray et al.(1982)认为植物护坡机理表现在植物地上部分的水文效应和根系的力学效应。Wu et al.(1979), Waldron et al.(1977)指出植物根系固土护坡力学机理在于根系可有效增强边坡土体黏聚力,从而提高边坡稳定性。在此基础上,借助于Mohr-Coulomb准则,Wu et al.(1979)推导出根系提高土体抗剪强度的解析解,即Wu-Waldron-model(WWM)模型,该模型假定由根系和土体组成的根-土复合体受到剪切作用后,一部分剪切力通过根系与土体间的摩擦力、咬合力和锚固力转化为根系的抗拉力,可用公式加以表示。
S=c+σtanφ+ΔSr
和
式中:S为复合体抗剪强度(kPa);c为土体黏聚力(kPa);σ为法向压力(kPa);φ为土体内摩擦角(°); ΔSr为由根系产生的土体抗剪强度增加值(kPa);θ和φ′分别为根系的剪切变形角(°)和复合体的内摩擦角(°);tr为复合体横截面上单位面积中单根平均抗拉强度(MPa);Arn/A为复合体横截面积上根系横截面积与土体横截面积之比值;Arn为复合体横截面上所有根系横截面面积(mm2);A为复合体横截面面积(mm2)。Wu et al.(1979), Thomas et al.(2010)、Leung et al.(2017)等在研究根系剪切变形角与土体抗剪强度的关系后,认为公式
亦可简化为
ΔSr=btr(Arn/A)或ΔSr=btr(tiai/A)
式中:b为系数,该值根据试验条件和植物种类不同可取值为1.15~1.2;ti为第i条根段的抗拉强度(MPa);i为第i条根;ai为第i条根的横截面积(mm2)。借助于WWM模型,Pollen et al.(2005)在研究根系对河岸边坡稳定的影响后,认为由WWM模型计算得到的复合体抗剪强度值较原位实测值高出40%~60%,其原因在于WWM模型假定复合体受到剪切后,由根系承担的拉应力同时发挥作用,而实际的工况是复合体受到剪切时,根系根据土体应变的变化而逐步发挥其抗拉强度。针对WWM模型的上述缺陷,Pollen et al.(2005)提出另一种模型,即纤维束理论模型(FBM),该模型假定基本符合复合体受到剪切时的实际工况。Schwarz et al.(2013)在对WWM模型和FBM模型进行综合分析后指出,尽管两种模型的假定条件存在差异,但两种模型均认为根系横截面积比(Ar/A)和单根抗拉强度(tr)是决定根系产生的土体抗剪强度增加值(ΔSr)的主要因素(Schwarz et al.,2013)。
目前,针对根系增强土体抗剪强度的理论模型研究主要集中于根系横截面积比(Ar/A)对土体抗剪强度增加值(ΔSr)的影响,对于植物单根抗拉强度(tr)对土体抗剪强度的研究,则主要局限于利用算术平均值求得其抗拉强度值。实际上,植物因其根径、根系含水量、生长环境等因素的差异,其抗拉强度间的差异相对较为显著,即使是同种植物根系,在相同含水量和根径条件下,其强度亦产生较大差异(Gary et al., 1982; 祁兆鑫等, 2017)。故利用算术平均值求得的单根抗拉强度值并不能代表其实际的抗拉强度值,因此采用合理的统计方法对植物单根抗拉强度进行计算,进而确定其单根抗拉强度代表值(tr)对于提高土体抗剪强度增加值(ΔSr)计算准确度,从而准确评价植物对边坡稳定性影响具有重要的意义。目前尚未见有基于统计理论计算植物单根抗拉强度值的相关成果报道。为此,本研究以生长于青海河南地区的草本植物黄花棘豆(Oxytropisochrocephala)、早熟禾(Poaannua)、紫花针茅(stipapurpwea)、青藏苔草(Carexmoorcroftii)和矮嵩草(Kobresiahumilis)为研究对象,分别采用正态分布、伽马分布、泊松分布、瑞利分布以及威布尔分布等数学统计模型,对上述植物根径(dr)、单根抗拉力(Rr)和单根抗拉强度(tr)等指标进行拟合分析,以确定上述5项指标具体服从的分布函数,从而为进一步开展根系增强土体抗剪强度分析选择合理的数学模型提供理论参考。
1 材料与方法
1.1 研究区概况
研究区青海省河南县启龙牧场(101°50′08″E, 34°35′12″N),位于青藏高原东北部黄河源,平均海拔为3600 m,年均温为0.31 ℃,年均降雨量为468.9 mm,相对湿度为66%,该区水资源较为丰富,主要河流为泽曲河、洮河、尕玛日河等,年均径流总量为1.39×1010m3,植被类型以垂穗披碱草(E.nutans)和矮嵩草(C.alatauensis)为主,其余伴生草本主要有早熟禾(P.annua)、紫花针茅(S.purpurea)、高山嵩草(K.pygmaea)、青藏苔草(C.moorcroftii)、珠芽蓼(P.viviparum)、紫菀(A.tataricus)、黄花棘豆(O.ochrocephala)等(刘昌义等, 2019)。区内地形地貌以缓坡平原为主,土壤类型以不良级配沙土为主(刘昌义等, 2019)。为查明研究区主要植物属种及类型,本课题组于2017年7~8月对区内植物类型开展了野外调查和室内鉴定,并对植物组合进行了分类。具体做法如下:首先在区内选择代表性地段实测地形线,然后按照地形线由坡顶至坡底方向,依次划分出若干不同类型的植物组合,图1所示为区内沿剖面线采样情况。采集区土壤类型为不良级配沙土,且土壤以氮、钾含量相对较高,磷含量较低为主要特点,土体含水率为18.33%~23.35%,土壤密度为1.03~1.13g·cm-3(刘昌义等, 2019)。
1.2 植物属种
黄花棘豆(O.ochrocephala)多年生草本,环境适应性较强,主要分布于青海东部和南部,海拔为1900~5200 m的荒山、平原草地、山坡草地、阴坡草甸、高山草甸、沼泽地、河漫滩、干河谷阶地、山坡砾石草地等区域(《中国植物志》编委会, 2004; 王文婷等, 2019)。
早熟禾(P.annua)为1年生或冬性禾草,主要生长于海拔为100~4800 m的平原和丘陵的路旁草地、田野水沟或荫蔽荒坡湿地,为重要的水土保持植物和荒地恢复先锋植物(《中国植物志》编委会, 2004; 杨庆楠等, 2019)。
紫花针茅(S.purpurea)为禾本科、针茅属多年生密丛草本植物,多生于海拔1900~5150 m的山坡草甸、山前洪积扇或河谷阶地上,为重要的水土保持或荒地恢复先锋植物(《中国植物志》编委会, 2004; 李光莹等, 2014; 周林虎等, 2019)。
青藏苔草(C.moorcroftii)为莎草科苔草属根茎密丛型湿中生多年生草本,耐寒性强,主要生长于海拔3500~5300 m的山坡草地、河边、沟边阶地、洪积扇、河漫滩、湖滨平坦草地、高山草甸、沼泽草甸草地、半荒漠带沙坡、草原、高山草甸、高山灌丛草甸、高山湖边草甸等地带(《中国植物志》编委会, 2004; 刘文胜等, 2018)。
矮嵩草(K.humilis)属多年生莎草科嵩草属草本植物,为典型的密丛型草类,属高抗逆性物种,构成矮嵩草草甸的主要建群种,具有耐寒、耐旱、耐辐射、耐强风及耐贫瘠的特点,是青藏高原高寒草甸草地的优良牧草,是涵养水源、保护生态多样性和碳素的优良植物(《中国植物志》编委会, 2004; 李积兰等, 2016)。
1.3 根系采集与处理
将试验前确定的半径为40 cm内的植物及土体(根-土复合体)用铁镐和铁铲挖出,放置于试样盆中,为防止水分蒸发,用塑料袋将整个试样盆及植物包裹,并将其及时带回实验室待测。试验开始前,将完整的复合体放置于盛满水的容器中,浸泡60 min以分离根系和附着于根系上的土粒,60 min后,将松散的土体和水倒出,然后再用水冲刷附着于根系表面的土体,以确保土体与根系完全分离; 最后,将去掉泥土的根系清洗干净,并用自封袋包裹以防止水分蒸发。在试验过程中,将上述根系剪为长度为8~10 cm的根段,夹持在室内单根拉伸试验仪上进行拉伸试验。
1.4 单根拉伸试验
本研究采用的单根拉伸试验仪工作原理和基本结构类似于电子万能试验机,该仪器主要包括根系拉伸系统和数据采集系统,其工作原理如图2所示(朱海丽等, 2009; 李可等, 2018; 刘亚斌等, 2018)。试验过程中,待根系夹持完毕后,启动仪器,根系受到拉伸,仪器自动采集并记录根系所有拉力和相应伸长量,直至根系发生破坏。在试验过程中为有效避免根系被拉出夹具,用橡皮胶带将夹头包裹以增加其与根系的摩擦力。为确保根径、单根抗拉力和单根抗拉强度等值具有一定的代表性,从密封袋中随机挑选60~70条根作为试验对象。
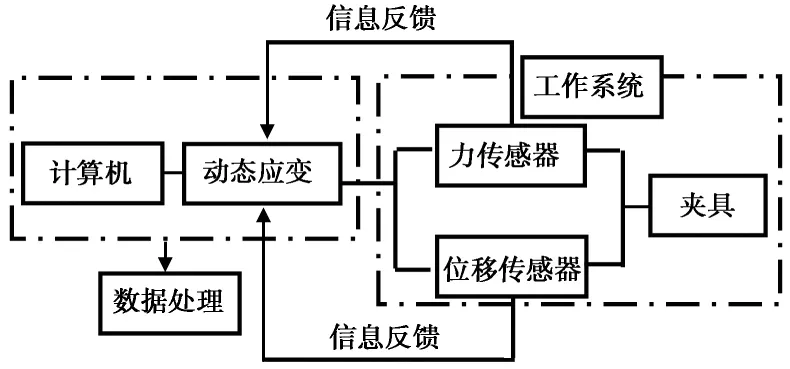
图2 单根拉伸试验工作原理(朱海丽等, 2009; 李可等, 2018; 刘亚斌等, 2018)Fig.2 Representation of tensile test apparatus
根据测得的单根根径(dr)和单根抗拉力(Rr),可通过式(1)计算单根抗拉强度(tr):
(1)
式中:tr为单根的抗拉强度(MPa);Rr单根断裂时的抗拉力(N);dr为单根直径(mm)。
1.5 数据分析方法
为分析5种植物根系三项指标(根径、抗拉力和抗拉强度)的分布特征,本研究采用正态分布、伽马分布、泊松分布、瑞利分布以及威布尔分布等数学统计模型对其进行分析。囿于论文篇幅,本研究并未给出上述分布的概率密度(probability density function, PDF)和累积概率函数(cumulative probability function, CPF),其相应公式可见文献(童行伟等, 2016)。
2 结果与分析
2.1 植物单根抗拉试验结果
利用根系力学测试系统,本研究共对上述5种植物根系开展了单根抗拉试验,其试验结果如表1所示。由该表可知,5种植物平均根径为1.48~0.27 mm,标准差为0.81~0.08 mm,变异系数为26.00%~55.16%; 单根抗拉力平均值为20.66~2.53 N,标准差为20.66~1.16 N,变异系数为107.63%~48.65%; 单根抗拉强度平均值为10.85~50.25 MPa,其标准差为24.39~10.68 MPa,变异系数为127.07%~37.78%。5种植物中,黄花棘豆其平均根径相对最粗,为1.48 mm,青藏苔草、矮嵩草和紫花针茅依次递减,分别为0.93 mm, 0.39 mm和0.29 mm,早熟禾平均根径相对最细,为0.27 mm; 对于平均单根抗拉力,黄花棘豆相对最大,为20.66 N,其次分别为青藏苔草、矮嵩草和紫花针茅,早熟禾单根平均抗拉力相对最小,该结果表明上述草本单根抗拉力随根径增加表现出逐渐增加的变化特征,该结论与李可等(2018)、朱海丽等(2009)和刘亚斌等(2018)研究结论一致。对比上述植物单根抗拉强度可知,5种草本植物中,紫花针茅平均单根抗拉强度相对最大,为50.25 MPa,矮嵩草、青藏苔草和早熟禾次之,黄花棘豆相对最小,为10.85 MPa,根据Wu et al.(1979)中关于“根系强度愈大,则其对土体抗剪强度贡献愈显著”的结论可知,紫花针茅、矮嵩草、青藏苔草和早熟禾对土体抗剪强度贡献相对较为显著,而黄花棘豆则相对不显著。

表1 研究区5种植物根系力学特征指标测试结果Table1 Mechanical indices of roots for five types of species
2.2 数学统计模型对数据的处理
2.2.1 供试植物根系各力学指标分布参数
为合理确定5种植物根径、抗拉力和抗拉强度服从何种分布,本研究分别采用了正态分布、伽马分布、泊松分布、瑞利分布以及威布尔分布对上述数据进行了处理,分析了在0.01置信水平下,5种植物三项指标的分布参数,其结果如表2~表4所示。
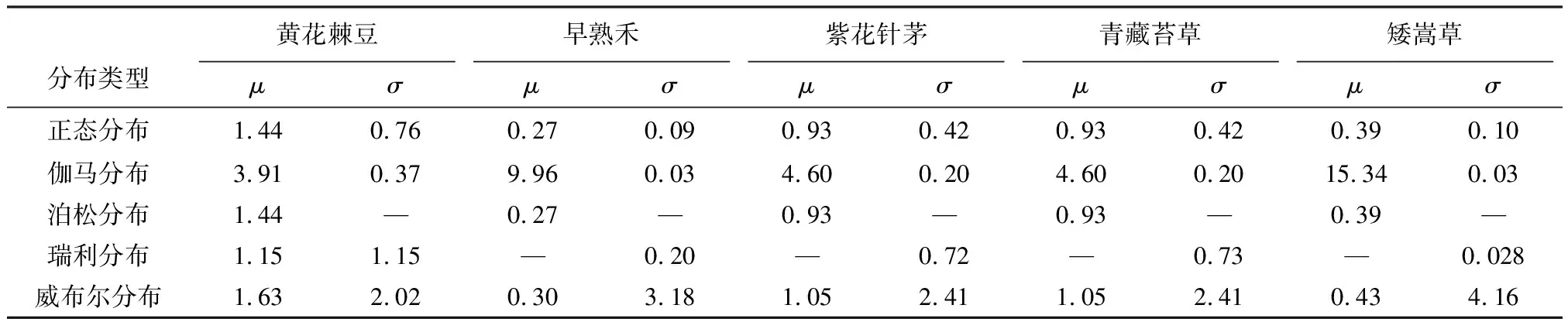
表2 不同分布模型下5种草本植物根径分布参数值Table2 Distribution parameters of root diameter for five species based on different statistical models

表3 不同分布模型下5种草本植物单根抗拉力分布参数值Table3 Distribution parameters of tensile resistance of root for five species based on different statistical models

表4 不同分布模型下5种草本植物单根抗拉强度分布参数值Table4 Distribution parameters of tensile strength of root for five species based on different statistical models
2.2.2 植物根系各指标值分布规律
将表2~表4中的相关数据,代入上述5种分布的概率密度函数公式,即可得到5种植物根径、抗拉力和抗拉强度值的不同概率密度曲线图(图3~图5)。对于根径,由图3所示可知伽马分布、威布尔分布、瑞利分布和正态分布均可较好地描述其分布,而泊松分布对其描述性相对较差。对图3a进一步分析可知,随着根径逐渐增加,黄花棘豆根径的分布频数(f(x))亦表现出逐渐增加的趋势,且对于除泊松分布以外的其他4种分布而言,其根径频数为最大值时,其相应的根径区间为1.0~1.5 mm,随着根径进一步增加,其根径分布频数则表现出递减的变化趋势。对于早熟禾,其根径主要分布为0.2~0.4 mm,且威布尔、伽马和正态分布对其根径分布规律的描述基本一致,而泊松分布则与其他分布具有显著性差异(图3b)。其余3种植物根径分布规律与早熟禾根径分布规律相类似,如图3c~图3e所示。

图3 5种草本植物根径概率密度分布Fig.3 Probability density distribution of root diameter for five speciesa.黄花棘豆; b.早熟禾; c.紫花针茅; d.青藏苔草; e.矮嵩草
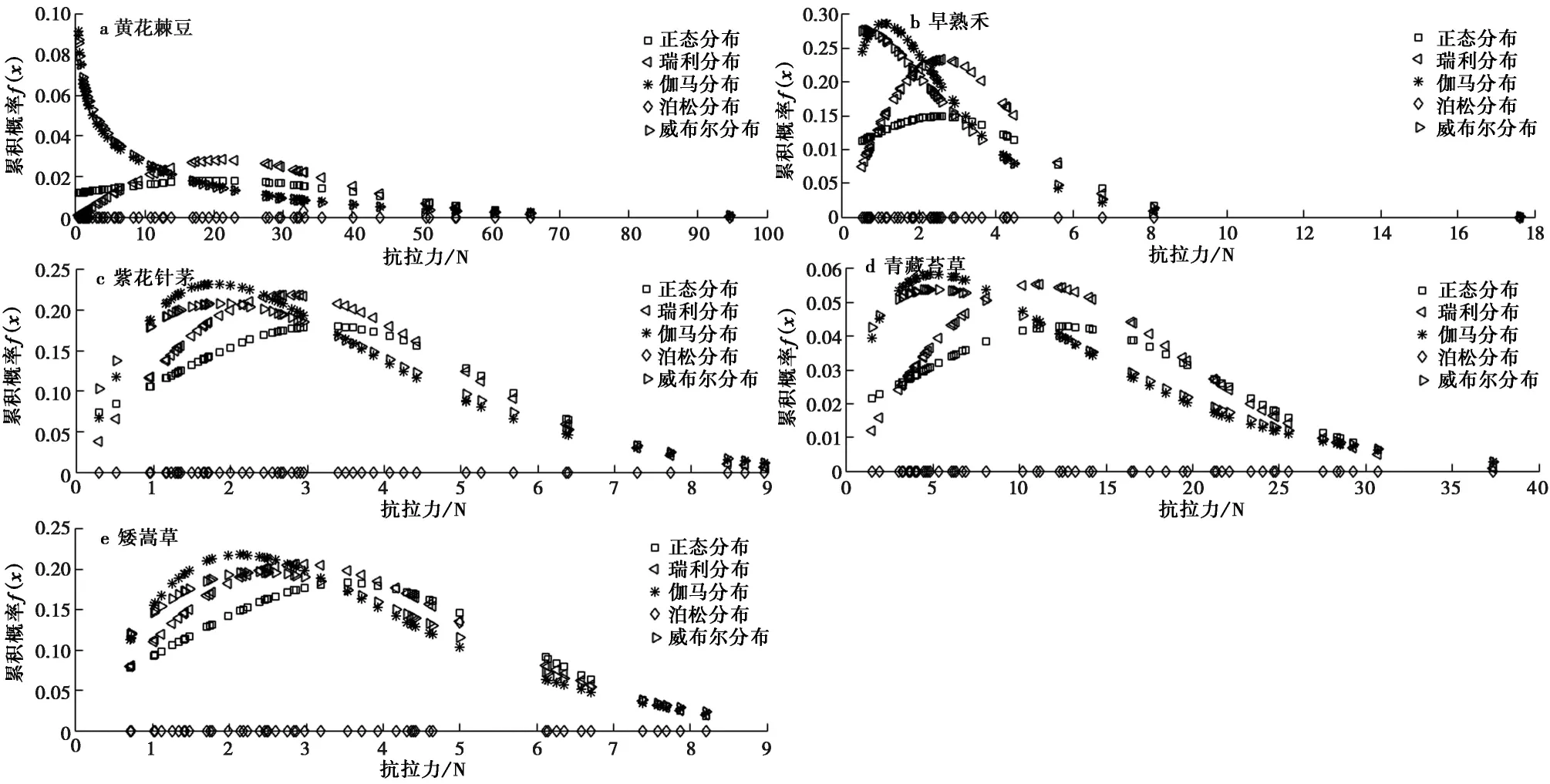
图4 5种草本植物根径单根抗拉力概率密度分布Fig.4 Probability density distribution of tensile resistance for five speciesa.黄花棘豆; b.早熟禾; c.紫花针茅; d.青藏苔草; e.矮嵩草

图5 5种草本植物根径单根抗拉强度概率密度分布Fig.5 Probability density distribution of tensile strength of roots for five speciesa.黄花棘豆; b.早熟禾; c.紫花针茅; d.青藏苔草; e.矮嵩草
对于单根抗拉力,5种草本植物单根抗拉力概率密度在不同概率下存在一定程度差异(图4)。由图4a可知,黄花棘豆的单根抗拉力分布频数f(x)在泊松分布条件下未产生变化,在伽马和威布尔分布下则表现出随抗拉力增加而呈单调递减的变化特征,而在瑞利和正态分布下则表现出先增加后减小的变化特征; 对于早熟禾,除泊松分布外,其余3种分布的分布频数随单根抗拉力增加表现出先增加后减小的变化特征,但其分布频数最大值所对应的单根抗拉力值在不同分布下存在较大差异,且其分布频数最大值所对应的抗拉力最值区间为0~5 N,该结果表明紫花针茅根系抗拉力主要位于该范围(图4b); 对于紫花针茅,在不同分布下,其单根抗拉力分布频数随单根抗拉力增加均表现出先增加后减小的变化特征,但泊松分布下,其分布频数曲线和其他4类分布存在显著差异,例如泊松分布下,其单根抗拉力分布频数随抗拉力增加表现出快速升高和降低特征,而其他4类分布下,则表现出逐渐增加和逐渐降低的变化特征,且其他4类分布下,其分布频数最大值对应的单根抗拉力值主要为2.0±0.5 N,该结果表明早熟禾单根抗拉力主要为1.5~2.5 N(图4c)。对于青藏苔草,在正态、瑞利、威布尔及伽马分布条件下,其单根抗拉力分布频数均随单根抗拉力增加表现出先增加后减小的变化特征,但其分布频数最大值所对应的最大值存在较大程度差异,例如正态分布下,其最大值对应的抗拉力值约为12 N,威布尔和伽马分布下,其最大值对应的抗拉力值约为6 N(图4d)。对于矮嵩草,其单根抗拉力值的分布规律与紫花针茅相类似(图4e)。
本研究中5种草本植物单根抗拉强度根据其概率密度可分为2类,即黄花棘豆为一组,其余4种草本为一组(图5)。对于黄花棘豆,在泊松分布下,其单根抗拉强度的分布频数随其抗拉强度增加表现出“线性-跳跃-线性”的变化特征,该现象表明在该分布下,其单根抗拉强度值为15 MPa,而在瑞利和正态分布下则表现出先非线性增加后非线性减小,再呈线性减小的变化特征,且其分布频数最大值约为25 MPa,该现象表明在上述2类分布下,其单根抗拉强度值主要为0~25 MPa。对于剩余4种草本,其单根抗拉强度频数值随抗拉强度增加表现出先增加后减小的变化特征,且同一草本在不同分布下,其强度频数最大值所对应的强度值相差不大,例如矮嵩草在4种分布下,其抗拉强度频数最大值所对应的强度值为25~35 MPa。
2.2.3 草本植物根系力学特性指标累积
为进一步分析上述植物根径、单根抗拉力和抗拉强度分布的累积概率特征,本研究将表2~表4中的相关数据带入5种概率分布的累积概率公式,即可获得相应分布条件下,5种草本植物根径、抗拉力和抗拉强度的累积概率分布特征曲线(图6~图8); 此外,为比较5种概率分布函数中,何种分布函数更能准确地描述三项指标的分布,本研究参考王正等(2017)中的“失效概率”的理念,利用中位秩公式和经验累积分布函数绘制了三项指标的实际分布概率曲线和经验累积曲线,通过对比5种分布函数曲线与实际分布概率曲线和经验累积曲线的相似度,优选相对更为准确的分布函数(图6~图8)。对于黄花棘豆和青藏苔草根径,由图6a和6d所示可知,除泊松分布表现出“阶梯”状的增加趋势外,其余4种分布的累积概率分布随根径增加表现出非线性增加趋势,且其分布曲线形态与极值累积分布函数曲线和实际分布概率曲线基本一致,该结果亦说明, 4种分布可较好描述黄花棘豆和青藏苔草根径分布; 对于早熟禾、紫花针茅和矮嵩草,伽马、正态和威布尔分布所描述的根径累积概率曲线一致,且与极值累积分布函数曲线和实际分布概率曲线相似,该结果表明相较于泊松分布和瑞利分布,正态、伽马及威布尔分布可较好地描述其根径分布,如图6b、图6c和图6e所示。

图6 5种草本植物根径累积概率分布Fig.6 Cumulative probability distribution of diameter of roots for five speciesa.黄花棘豆; b.早熟禾; c.紫花针茅; d.青藏苔草; e.矮嵩草
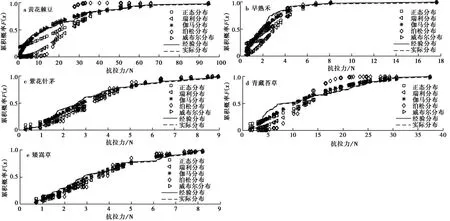
图7 5种草本植物抗拉力累积概率分布Fig.7 Cumulative probability distribution of tensile resistance for five speciesa.黄花棘豆; b.早熟禾; c.紫花针茅; d.青藏苔草; e.矮嵩草

图8 5种草本植物抗拉强度累积概率分布Fig.8 Cumulative probability distribution of tensile strength of roots for five speciesa.黄花棘豆; b.早熟禾; c.紫花针茅; d.青藏苔草; e.矮嵩草
对于黄花棘豆单根抗拉力,由图7a所示可知,瑞利和泊松分布函数所描述的单根抗拉力累积分布曲线与其经验累积分布函数曲线和实际分布概率曲线相差较大,而威布尔、正态和伽马分布所描述的单根抗拉力累积分布概率与经验累积分布函数曲线和实际分布概率曲线较为接近,该结果表明,威布尔、正态和伽马分布可较好描述黄花棘豆单根抗拉力的概率分布; 对于早熟禾、紫花针茅和矮嵩草,由图7b、图7c和图7e所示可知除泊松分布外,其余分布的累积概率曲线与经验累积分布函数曲线和实际分布概率曲线基本一致,该现象表明正态、伽马、瑞利和威布尔分布均可较好地描述上述3种植物单根抗拉力分布; 对于青藏苔草,由图7d所示可知,正态、威布尔和伽马分布的累积概率曲线与经验累积分布函数曲线和实际分布概率曲线基本一致,该现象表明,上述3种分布可较好地描述青藏苔草单根抗拉力分布。
对于5种草本植物抗拉强度,由图8所示可知,除泊松分布外,在剩余4种分布下,5种草本抗拉强度累积概率曲线与其经验累积分布和实际分布概率曲线基本一致,该结果表明正态、威布尔、伽马及瑞利分布,均可较好描述其上述5种草本单根抗拉强度的概率分布。
2.2.4 植物根径、抗拉力及抗拉强度的K-S分布检验
为进一步定量讨论5种草本植物根径、抗拉力和抗拉强度所服从的分布函数,本研究采用柯尔莫哥洛夫-斯米洛夫检验(K-S)对其进行了检验,检验结果如表5所示。由该表可知,5种草本其根径、抗拉力和抗拉强度表现出不同的分布特点,即:(1)5种草本3项指标均不服从泊松分布,仅有个别指标服从瑞利分布,根径均服从正态分布,伽马分布和威布尔分布,个别服从瑞利分布,抗拉力和抗拉强度均服从伽马分布和威布尔分布,个别植物服从瑞利和正态分布; (2)5种草本3项指标的最优分布函数为伽马分布、威布尔分布或正态分布; (3)5种草本根径最优分布函数均为伽马分布(紫花针茅为威布尔分布),抗拉力最优分布均为伽马分布(矮嵩草为威布尔分布),紫花针茅根系抗拉强度最优为正态分布、青藏苔草和矮嵩草为伽马分布、早熟禾与黄花棘豆最优分布均为威布尔分布。

表5 5种植物根径、抗拉力/抗拉强度分布K-S检验结果Table5 K-S tests for root diameter, tensile resistance/strength distribution
3 讨 论
利用统计学原理对植物生长指标进行统计并获得其服从何种分布的相关研究由来已久(Mcgarrigle et al.,2011; 胡焕香等, 2012; Effertz et al.,2016; Sapkota et al.,2019),如汪少华等(2018)采用Weibull模型、负指数模型、修正指数模型、混合Weibull等模型对古尔班通特沙漠的梭梭(H.ammodendron)根径结构分布进行了模拟,指出相比较于其他几种分布模型,Weibull及混合Weibull模型可较好地描述该地区梭梭基径的分布。本研究所涉及的5种草本植物,其根径分布亦服从正态、瑞利、威布尔和伽马分布,该结论与上述学者研究结论基本一致,但需指出的是,是否所有植物根径均服从正态、瑞利、威布尔和伽马分布尚需进一步分析。此外,本研究中,5种植物根径最优分布为伽马分布,而非文献Sapkota et al.(2019)、Diamanto ̄poulou et al.(2015)所认为的威布尔分布或正态分布,造成本研究结论和上述学者论文结论不一致的原因在于植物的根径的差异,如Sapkota et al.(2019)、Diamantopoulou et al.(2015)所研究的植物为乔木植物,其根径差异较大,而本论文中,所研究的植物为草本植物,其根径较小,变化范围相对不大。
植物单根抗拉力和抗拉强度是衡量根系对土体抗剪强度贡献值的重要指标(Waldron, 1977; Gary et al., 1982; Thomas et al., 2010; 祁兆鑫等, 2017)。采用分布函数对机构或工件的承载力或强度进行统计研究,主要集中在材料、机械等领域(Wang et al., 2014; 顾梦元, 2014; 王正等, 2017),通过已有文献可知,尚未有采用统计学理论对植物单根抗拉力和抗拉强度进行统计,进而获得其单根抗拉力和抗拉强度方面的相关报道。根系因其生长环境、生长期、属种以及根系部位等差异,其单根抗拉力和抗拉强度存在较大差异(Reubens et al.,2011; Caviezel et al.,2014),这些差异为合理计算根系对土体抗剪强度贡献带来了一定影响,如本研究中5种草本植物单根抗拉强度的变异系数分别为127.07%、46.28%、48.53%、73.15%和37.78%,由这些变异系数可知,标准差的最大值甚至大于相应的平均值,这在较大程度上导致由WWM求解得到的土体抗剪强度产生显著性差异。因此,采用统计学原理对根系力学指标进行计算则尤为必要。
本研究中5种植物单根抗拉强度分布函数均为威布尔分布,这体现出威布尔分布可较好的拟合材料破坏这种特性,即威布尔分布假设认为:材料是由若干个相互串联的、强度不一的小元件组成的链条,整个材料的强度取决于元件中强度最低的那个元件,每个元件的强度为一随机变量,且各元件强度相互独立且服从相同分布,则整个材料的强度概率分布可归为极小值分布问题,因此,材料的强度亦也取决于其最弱环的强度,故可用威布尔分布进行描述(顾梦元, 2014)。此外,除威布尔分布外,部分植物根系抗拉强度最优分布服从正态分布和伽马分布,导致这些植物根系抗拉强度最优分布服从这两种分布的原因需进一步分析。
4 结 论
本研究通过对青海省河南县高海拔高山草甸的5种草本植物开展单根抗拉试验,获得其根径、单根抗拉力和抗拉强度等指标,并借助于统计理论对上述指标的分布进行了系统的分析和研究,获得以下结论:
(1)研究区5种植物根径为1.48~0.27 mm,标准差为0.81~0.08 mm,变异系数为26.00%~55.16%; 单根抗拉力平均值为20.66~2.53 N,标准差为20.66~1.16 N,变异系数为107.63%~48.65%; 单根抗拉强度平均值为10.85~50.25 MPa,其标准差为24.39~10.68 MPa,变异系数为127.07%~37.78%。
(2)在威布尔分布、正态分布、瑞利分布、泊松分布和伽马等5种分布中,泊松分布对上述5种植物根径、单根抗拉力和抗拉强度分布的描述效果相对较差,威布尔分布、伽马分布和正态分布对上述5种指标分布的描述效果相对最好,其余分布对不同指标分布的描述效果则居于两者之间,且不同植物对上述分布的适用性表现出一定程度的差异。
此外,除威布尔分布外,部分植物根系抗拉强度最优分布服从正态分布和伽马分布,导致这些植物根系抗拉强度最优分布服从这两种分布的原因需进一步分析。

