超声波电机离散采样迭代学习逆控制

黄文文，宋 璐，史敬灼

(河南科技大学 电气工程学院，河南 洛阳 471023)

0 引 言

迭代学习控制(Iterative Learning Control，ILC)利用前次控制量和误差信息来提高当前控制性能的学习控制思想，使其在未知、不确定的重复扰动作用下，仍然能有良好的控制性能。迭代学习控制思想自提出以来，因其不同于传统控制策略的特点而被广泛关注。文献[1-2]尝试将迭代学习控制策略应用于超声波电机转速控制，表明迭代学习控制策略适用于超声波电机运动控制，但所得控制效果仍不够理想，有待进一步研究。

目前，超声波电机迭代学习控制系统普遍采用基于离散采样的数字实现方式[3-4]，其分析及设计方法均有别于定义在连续域上的传统迭代学习控制。无论是从理论分析还是从实际应用的角度来看，都有必要对离散采样形式的迭代学习控制方法进行研究，为超声波电机控制系统的设计提供理论基础和设计原则。

本文针对超声波电机转速控制需求，以离散采样的超声波电机控制系统为分析对象，基于数字控制思想，分别在时域和频域对离散采样ILC的动态特性进行分析，推导ILC控制过程单调收敛的判据，给出ILC控制器设计方法。基于推导结果，设计超声波电机离散ILC转速控制器，进行仿真分析和实验验证，进一步讨论了ILC控制律的学习收敛性质和控制性能。良好的控制效果表明，推导所得结论及控制器设计方法正确，所提超声波电机离散迭代学习逆控制策略有效。

1 离散系统ILC分析

不失一般性，考虑如下迭代学习控制律

uk+1,i=H(q)[uk,i+pL(q)ek,i+1]
ek,i=yr,i-yk,i

(1)

式中，H(q)为滤波函数；L(q)为学习函数；q为转移算子；p为学习增益，p>0；k为迭代次数；yr,i为给定值或期望输出；yk,i为如下系统的输出

xk,i+1=Φxk,i+Γuk,i
yk,i=Cxk,i

(2)

该系统的初始状态为xk(0)。又有

xr,i+1=Φxr,i+Γur,i
yr,i=Cxr,i

(3)

式中，xr为期望的系统状态变量，ur为期望输出对应的输入控制量。

式(3)与式(2)相减，得

Δxk,i+1=ΦΔxk,i+ΓΔuk,i
ek,i=CΔxk,i

(4)

其中，Δxk,i=xr,i-xk,i，Δuk,i=ur,i-uk,i，并假设初始条件e(0)=0成立。

式(1)所示控制器的设计，就是设计适当的L(q)和H(q)，使系统误差的最大值能在迭代学习过程中渐进收敛于0。

在迭代学习控制器的设计过程中，系统的相对阶数是一个关键参数，对控制性能与具体实现都有重要影响。例如，考察相对阶为n的n阶单输入单输出系统

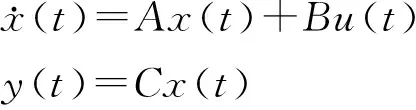
(5)

因该系统的相对阶为n，由

(6)

可知CAn-1B不为0，而CB至CAn-2B均为0。以采样时间T将式(5)离散化，得采样系统的输入增益为

(7)

式(7)左乘C可得

(8)

可见，采样后，系统的相对阶数由n变为1。这一结论，也可由下式推出

yi+1=CΦxi+CΓui

(9)

此结果表明，在连续时间情况下，ILC需要计算输出信号的n阶导数，而采样迭代学习控制则不需要。不需要考虑时间的先后顺序和相对阶，大大简化了离散系统ILC的推导过程。式(9)中，CΓ的大小取决于采样时间和系统阶数。

1.1 时域分析

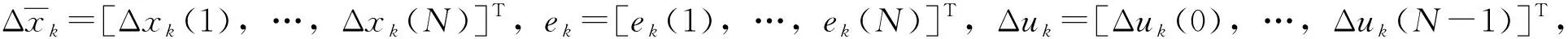
(10)

若假设有理函数H(q)和L(q)都满足因果关系，通过分子除以分母，可将其展开为无穷级数，得H(q)=h0+h1q-1+…，L(q)=l0+l1q-1+…,由此，将H和L展开，写为矩阵形式，它们均为下三角Toeplitz矩阵，级数的前N个系数为Toeplitz矩阵的第一列元素。

在式(1)等号两边，同时用ur,i做减法，可得

Δuk+1=HΔuk-pHLek+(1-H)ur

(11)

式中，ur=[ur(0),…,ur,(N-1)]T，将式(10)代入式(11)可得

Δuk+1=H(I-pLP)Δuk+(I-H)ur

(12)

记F=H(I-pLP)，易知F有重特征值h0(1-pl0CΓ)，则式(12)的稳定性条件为

|h0(1-pl0CΓ)<1|

(13)

如前所述，在采样迭代学习控制系统中，因CΓ=0，故式(13)是能成立的。需指出的是，条件(13)是有界输入和有界输出系统稳定的充分条件，并不能保证‖ek‖单调减小。下面，考察式(12)中定义的F来进一步研究ILC的收敛性。若取H(q)=L(q)=1，则式(12)成为

Δuk+1=(1-pP)Δuk

(14)

因其等价于比例控制器，这种控制形式被称为P型ILC。对应的稳定性条件可简化为

|1-pCΓ|<1

(15)

在时域中，如果|1-pCΓ|<1，且满足

(16)

则可保证单调收敛[5]。

显然，选取合适的学习函数L(q)，可以增加满足上述条件的可能性。由上述表达式，还可以看出采样时间对ILC收敛性的影响。式(16)中的参数N表示每次迭代控制过程中的采样数据个数。对于指定的系统，N值越小，不等式(16)就越容易成立。需要注意的是，这些分析仅对理想的无扰动稳定线性时不变系统是成立的。若系统受到可重复性扰动的作用，则需选择合适的采样时间以覆盖扰动带宽来抑制扰动影响。因此，在实际系统中，采样时间值的选取往往需要折衷考虑。

1.2 频域分析

由以上分析可知，基于时域的分析仅能保证BIBO的稳定性，系统不一定能表现出理想的控制性能。因此，需寻求能够保证渐进收敛的判定条件。

对式(4)做z变换，得

ΔXk(z)=(Iz-Φ)-1ΓΔUk(z)
Ek(z)=CΔXk(z)=C(Iz-Φ)-1ΓΔUk(z)

(17)

式中，记C(Iz-Φ)-1Γ为P(z)。

对式(1)进行z变换，并用Ur(z)同时减去等号两边的表达式，得

ΔUk+1(z)=H(z)[ΔUk(z)-zpL(z)Ek(z)]+

[1-H(z)]Ur(z)

(18)

将式(17)代入式(18)得

ΔUk+1(z)=H(z)[1-zpL(z)P(z)]ΔUk(z)+

[1-H(z)]Ur(z)

(19)

式中，记H(z)[1-zpL(z)P(z)]为F(z)。将F(z)展开为F(z)=f0+f1z-1+f2z-2+f3z-3+…，此级数的前N个系数为Toeplitz矩阵F的第一列元素。

若F(z)是稳定的，并符合因果关系，则下式成立

(20)

式中，θ=ωkT。

于是，F的矩阵范数为‖F‖<1，式(20)表明范数‖ek‖是单调减小的，即满足单调收敛性。P(z)稳定是式(20)成立的前提。在实际系统中，P(z)可能并不稳定，可以通过增设内环反馈控制项来使P(z)稳定。

下面讨论能够保证单调收敛的L(q)和H(q)的选择准则。不失一般性的，假设P(z)是稳定的且无反馈环。

假设H(z)=1。理想情况下，选择L(z)=1/zpP(z)，能够得到单调意义下最快的收敛速度。但对于实际系统，P(z)是不可能准确得到的。单调收敛要求[1-pzL(z)P(z)]在以复平面原点为圆心的单位圆内，即要求pzL(z)P(z)在复平面上以(1,0)为圆心的单位圆内。具备稳定性需满足

(21)

另外，zL(z)需满足当|∠(ejθL(ejθ)P(ejθ))|→π/2时，|PejθL(ejθ)P(ejθ)|→0。

选择H(z)时，需考虑使1-H(z)最小并尽可能在稳态时接近0，进而避免稳态误差。因此，H(z)通常选为低通滤波器。由式(20)可知

(22)

这表明，如果设计H(z)的增益小于1，可使指定频率处的稳定区域增大。

2 超声波电机迭代学习逆控制仿真分析

以平方误差积分值(ISE)和绝对误差积分值(IAE)作为衡量误差值是否随着迭代学习进程而单调收敛的指标，二者的算式分别为

(23)

(24)

ILC所采用的控制律为

u(k,i)=u(k-1,i)+p*e(k-1,i+1)

(25)

式中，p为学习增益，k为迭代次数，u(k,i)为第k次迭代过程中i时刻的控制量，e(k-1,i)为第k-1次迭代过程i时刻的转速误差。

由于被控对象的惯性，i时刻所施加控制量的作用效果在i+1时刻才得以体现，即e(i+1)反映了u(i)的控制效果，故采用式(25)形式的控制律有可能得到较好的控制效果。

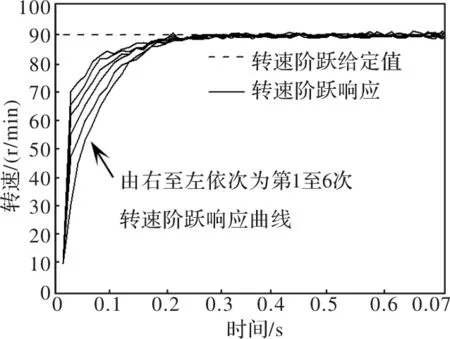
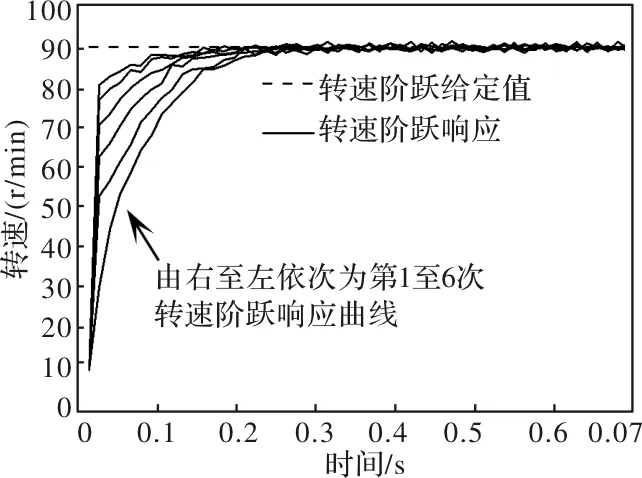
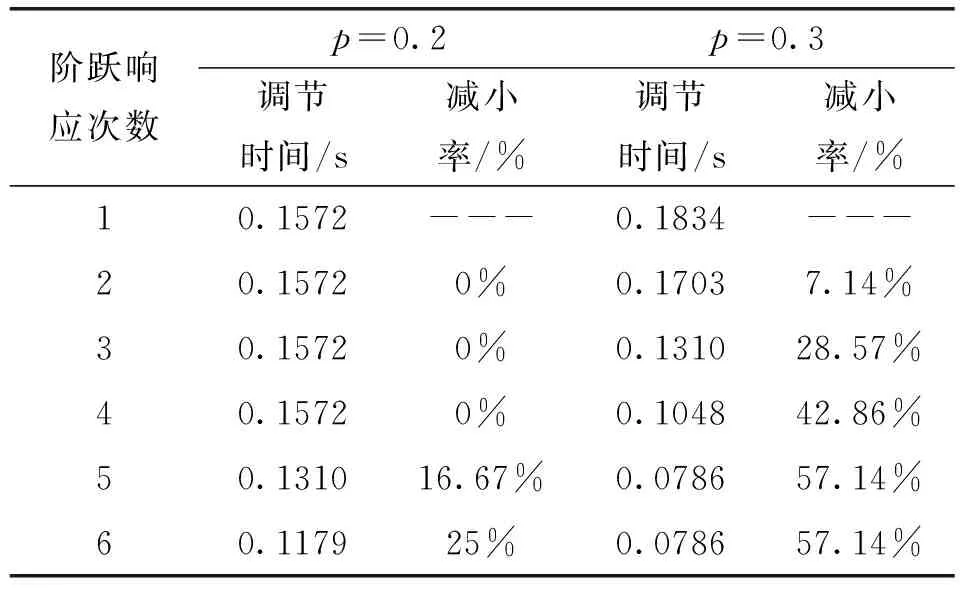
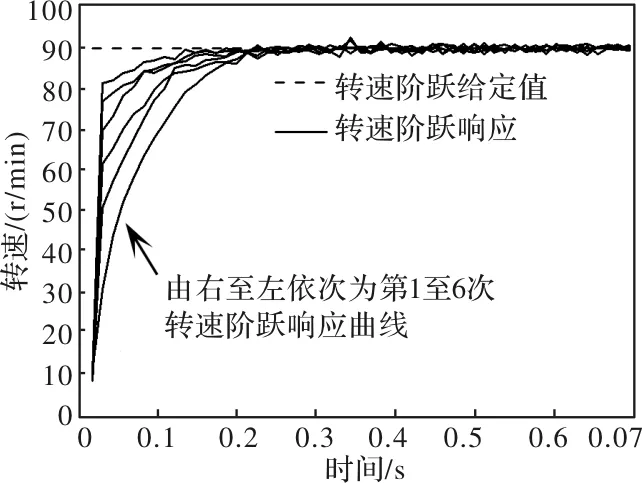
p是控制律式(25)中的唯一待定参数，其取值对控制性能有显著影响。根据上述分析，为保证稳定性，需满足|1-pCΓ|，由此可得0

3 实验研究

实验用电机为Shinsei USR60两相行波超声波电机，驱动电路为H桥结构，采用相移PWM控制方式。

将转速阶跃给定值设为90 r/min，采用与仿真相同的控制参数值进行迭代学习转速控制实验，实验结果如图1所示，转速逐渐趋于给定值，无超调，且随着迭代学习的进行，调节时间持续减小，从第1次到第6次阶跃响应调节时间减小幅度为25%，表明所述迭代学习控制策略有效。

图1 转速阶跃响应曲线(实测，p=0.2)

将转速阶跃给定值分别设定为30 r/min、60 r/min，控制参数不变，得到的实验结果表明两种阶跃给定值情况下，转速阶跃响应曲线均逐渐趋于给定值，无超调，但不同转速给定值下学习效果有差异，转速给定值为30 r/min的情况，从第1次到第6次阶跃响应调节时间减小幅度为77.78%，而转速给定值为60 r/min的情况为15.38%。

在起始阶段，转速较小时，六次阶跃响应曲线之间的差异较大，迭代学习持续改进的效果较为明显；随着转速增大，曲线之间的差异渐小。其原因在于，控制律式(25)中的控制量“修正项”与转速误差成正比；随着电机转速增大、误差减小，迭代学习带来的控制性能改进必然随之减弱。也是由于同样的原因，如果一个控制参数p值在低转速给定值情况下表现良好，那么，同样的p值用于高转速给定值情况，会使控制量增加较慢，迭代学习效果减弱。

将p值增至0.3进行迭代学习转速控制实验，90 r/min给定值情况下实验结果如图2，相比于图1，图2的转速动态上升速度更快，迭代学习带来的控制性能逐次改善更为明显。

图2 转速阶跃响应曲线(实测，p=0.3)

表1给出了图1、图2两种控制参数情况下阶跃响应调节时间对比，表中“减小率”为当前次阶跃响应调节时间相对于第1次阶跃响应调节时间的减小量，可表征迭代学习收敛过程的快慢。观察表1数据可知，增大p值后，调节时间随迭代的进行持续减小，且第三次阶跃响应调节时间的减小率已大于p为0.2情况下的最大减小率，迭代学习效果明显增强，可见p值增大后，控制性能有所改善。以上结果表明，p值对迭代学习收敛速率和时域控制性能有明显影响。采用所述控制律，在不同转速给定值情况下，通过适当调整p值，均可获得较好的迭代学习控制效果。

表1 不同p值情况下迭代学习控制性能指标(90 r/min)

进行间歇加载实验，以评估所述迭代学习控制策略对可变负载扰动的适应能力。间歇加载意为，在连续进行的6次阶跃响应实验过程中，仅对第2次和第4次施加负载，其它4次为空载。采用与前述空载实验相同的控制参数值进行间歇加载实验，得到转速阶跃响应如图3所示。转速阶跃响应曲线渐次改进，未出现转速跌落或稳态误差，表明在此控制律作用下，能够使控制量发生相应的变化以应对负载扰动，对负载扰动具有一定的适应能力。

图3 转速阶跃响应曲线(实测，p=0.3,第2、4次阶跃响应负载0.2 Nm)

4 结 论

目前，迭代学习控制普遍采用基于离散采样的数字实现方式，其分析及设计方法均有别于定义在连续域上的传统迭代学习控制。本文以充分发挥迭代学习控制能力、提高超声波电机控制性能为目的，基于离散采样系统的特征，分别从时域和频域两个角度，对ILC的控制特性及收敛性进行理论分析，分别给出了时域和频域的单调收敛判据和ILC设计方法，对ILC的工程应用具有指导意义和实用价值。在此基础上，提出超声波电机转速逆控制结构，以非线性逆模型来抵消超声波电机及其驱动装置的主要非线性特征，并设计ILC控制器来校正电机系统的线性动态特性。仿真及实验结果表明，所提控制策略及控制参数设计有效，超声波电机的转速动态响应表现出渐进的学习收敛过程，对负载间歇跳变等外加非重复扰动具有一定的适应能力，控制效果良好。